基于双边矢量概率矩阵的故障诊断方法研究

张 昭，陈 展，佘敦俊

(1.中国航天科工集团公司，北京 100854；2.海装驻北京地区第三军事代表室，北京 100074；3.北京机电工程研究所，北京 100074)

0 引言

在信息化作战中，武器装备呈现出技术含量高、使用强度高、损失和消耗数量大等特点，对武器装备及时有效的诊断维修，将对战争进程和结局产生决定性的影响。

随着多专业和学科的不断融合，针对武器装备领域故障诊断技术的研究，国内外学者做了不少相应的工作，并取得了一定的成果。美国华盛顿大学工程学院的Nathaniel Guy博士，从时序的角度对武器装备上遥测数据进行分析，以数据相关性的可视化过程为判定依据，从数据间的依赖关系和正常的相关关系间的偏差来判断系统是否发生故障[1]。梁瑞胜、孙有田、周希等人提出了一种基于小波包变换的残差能量方法，对武器装备动态测试数据进行分析处理，得到武器装备的故障特征，在此基础上利用神经网络实现了故障诊断和定位[2]。英国赫尔大学工程与计算机科学学院的Sohag Kabir博士利用故障模式影响、危害分析报告，结合故障树分析法对武器装备的故障可能性进行分析[3]。上述三种方法要求测试分析人员对武器装备的整个工作流程细节了解的非常清晰透彻，且需要大量完备的测试数据作为支撑。

紧密结合工程实际，研究目前复杂装备诊断领域相关内容，当前基于自动测试系统的测试结果中存在很多“不知道”、“不明确”、“不一致”等不确定因素，且测试样本数据呈现“小子样”、“不完备”的特点；上述的诊断方法难以适应这类复杂装备的诊断。而概率在解决复杂系统不确定性和关联性引起的故障有很大的优势。因此，提出了一种基于双边矢量概率矩阵的故障诊断方法。

1 双边相关性矩阵

1.1 相关性矩阵

“相关”表示两个元素Xi和Yi是彼此关联、相互牵涉的，即表示两元素之间的共享关系或因果关系。相关性矩阵则是表示两组元素X={X1,X2,...,Xi,...,Xn}、Y={Y1,Y2,...,Yi,...,Yn}之间的因果关系。

1)故障原因和故障模式间的相关性矩阵:

通过对复杂装备的FMEA报告分析可以获取故障原因节点集合c={c1,c2,...,ci...,cr}和故障模式节点集合m={m1,m2,...,mi...,mm}，故障原因-故障模式相关性矩阵的具体定义如下[4]：

(1)

2)故障模式和测试项目间的相关性矩阵:

通过分析故障模式与信号、信号与测试项目之间的相关性，以获取故障-信号-测试模型而生成测试与故障模式之间的依赖关系。

故障模式-测试相关性矩阵的具体定义如下：

(2)

1.2 双边相关性矩阵

故障原因-故障模式相关性矩阵Cm*n和故障模式-测试项目相关性矩阵Dm×n分别表示了故障原因与故障模式、故障模式与测试项目间的因果关系，对两个矩阵进行合并生成双边相关性矩阵，如式(3)所示：

Bm*(n+r)=Cm×r⊕Dm×n=

(3)

即双边相关性矩阵实现了故障原因、故障模式、测试项目三者之间的因果关系的表达。可以利用双边相关性矩阵中各个元素取值判定它们之间的相关性关系，即双边相关性矩阵Bm×(n+r)中元素cij取值为1时，表示故障原因ci与故障模式mj相关，相反，元素cij取值为0时，则表示故障原因ci和故障模式mj间不相关；双边相关性矩阵Bm×(n+r)中元素djk取值为1时，表示故障模式mj与测试项目tk相关，相反，元素djk取值为0时，则表示故障模式mj和测试项目tk间不相关。

2 故障原因-故障模式-测试项目双边矢量概率矩阵

2.1 双边矢量矩阵

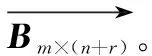
图1 双边矢量矩阵求取流程图

2.2 双边矢量概率矩阵

图2 基于后验思想的参数求取

1)基于模糊层次分析法的先验条件概率估计:

由于专家评价指标体系的结果往往具有不全面性、不确定性和模糊性的特点，故考虑将三角模糊数与层次分析法相结合。两者结合的优点是：数学模型更为简单，比较容易掌握；通过严谨的科学计算和逻辑推理，尽可能地降低主观因素影响的程度；可以较好的符合客观事实，对多层次、多因素的复杂问题评判效果比较好，使得“指标越优权重越大”。

基于层次分析法理论的基础上，针对客观事物的复杂性、决策者认识的局限性和判断的不确定性等情况，结合三角模糊数的理论，引入了三角模糊数层次分析(triangular fuzzy analystic hierarchy process，TFAHP)[6]。

(4)

专家的平均评分模糊数为：

(5)

取专家的平均评分模糊数的期望值为先验概率P(t|m)：

(6)

(7)

2)基于多源信息融合的后验条件概率确定：

在装备研制、生产和使用过程中不断产生的测试数据，例如子系统的历史测试数据、虚拟仿真信息和相似产品信息。将测试样本数据与先验概率融合，有助于概率模型更加贴近于实际。故本处采用贝叶斯理论[7]，对装备测试的历史数据进行融合，可得下式：

π(t|f)=f(P;α+n,β+N-n)

(8)

(9)

其中:N表示测试次数，n表示通过测试的次数，亦即当次测试可以检测出f的故障模式(已发生)，推理过程可参考文献[8]。

(10)

2.3 基于双边矢量概率矩阵的故障诊断技术

故障诊断是在故障原因-故障模式-测试项目双边矢量概率矩阵基础上，根据测试结果利用推理算法进行故障原因定位，从所有可能的故障模式中找出可能性最大的，进而定位到可能性最大的故障原因，整个诊断流程如图3所示。

图3 诊断流程图

在诊断流程中，首先通过测试项目的判定规则对来自武器装备的测试数据进行分析处理，针对测试数据不满足判定规则的情况，利用故障原因-故障模式-测试项目双边矢量概率矩阵，分析不通过的测试项目对应的所有故障模式及故障原因发生的可能性，提取最大可能性的故障模式及故障原因作为诊断结果。

3 试验结果与分析

3.1 某装备的局部FME(C)A分析

以某装备的局部FME(C)A分析报告为基础，分析故障原因、故障模式、检测手段等方面信息，得出故障原因包括：电阻网络短路c1、通用门电路短路c2、晶振电压不当c3、运算放大器N9功能失效c4，故障模式包括：供电指令未发出m1、RS422接口不工作m2和PU模块工作状态错误m3，测试项目包括：供电指令检查t1、RS422接口检查t2和PU模块工作检查t3。分析故障原因、故障模式、测试项目间相关性关系，按照公式(3)构建双边相关性矩阵B3×(3+4)，如表1所示。

表1 故障原因-故障模式-测试项目双边相关性矩阵B3×(3+4)

3.2 构建双边矢量概率矩阵

表2 故障原因-故障模式-测试项目双边矢量矩阵

表3 对于事件发生概率语言值

3.3 基于双边矢量概率矩阵的故障诊断

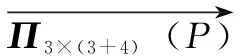
通过上述的双边矢量概率矩阵可以有效地将故障原因、故障模式、测试项目、系统工作流程和历史试验数据有机的结合起来，解决相关性矩阵中大部分故障模糊组的解耦问题。

4 结束语

本文以FMEA报告、专家经验为基础，获取表示故障原因与故障模式、故障模式与测试项目间的因果关系的双边相关性矩阵，利用测试项目和故障模式的相关性强弱和测试顺序构建矢量矩阵，并通过模糊层次分析法和贝叶斯理论获取双边矢量矩阵概率参数，为工程应用中武器设备的测试采样点布置不全、测试信息丢失所导致“不确定”、“小子样”、“不完备”等困难条件下的故障诊断提供了一种新思路。