基于数据挖掘的建筑能耗异常检测研究
段中兴,梅思雨
(1.西安建筑科技大学 信息与控制工程学院,西安 710055; 2.西部绿色建筑国家重点实验室,西安 710055)
0 引言
随着建筑行业的不断发展,建筑能耗监管系统的运行使海量的能耗数据在数据库中不断积累,由于能耗监管系统异常、设备存在故障等问题,建筑能耗数据中往往存在异常值,利用数据挖掘的方法寻找海量能耗数据中存在的异常能耗并对这些能耗异常值进行分析,有助于建筑运营管理者及时发现和解决建筑运行过程中可能存在的问题,针对性地对建筑内部产生的故障进行诊断。目前,已有许多学者针对能耗异常检测开展了大量研究工作。例如,文献[1]提出了一种基于数据挖掘技术的建筑能耗实时监测方法,通过将DBSCAN算法与分类方法相结合,对建筑能耗值进行类别提取并识别出新产生能耗值所属类别,从而判断其是否为异常值;文献[2]在广义离群值检测(GESD)的基础上改进得到了Modified z-score算法,该算法在检测离群点的同时能够反映出离群数据的离散程度,适合于建筑能耗数据的检测。这些方法虽然能够实现对建筑异常能耗数据的检测,但当样本空间密度分布不均或类间距差异很大时,检测结果会出现偏差,且不能对能耗数据进行快速处理。从能耗数据本身看,其中异常值仅在整个能耗数据中占很小的比例,即正常和异常能耗数据在数量上存在很大差异,属于不平衡数据类型,那么对于能耗异常检测问题,实质上则可以看作不平衡数据聚类,通过对能耗数据聚类,得到正常能耗(多数类)和异常能耗(少数类)类别,从而有效检测出能耗数据中的异常值,并给出针对性的诊断。不平衡数据,即数据集中不同类别所含样本在数量上存在很大差异,或不同类别所含样本数量相同但分布不均匀,是数据集中普遍存在的一种数据类型,存在于实际生活中的各个领域(如欺诈检测、网络入侵、医疗检查等)。目前已有的大多数经典聚类方法对于平衡数据聚类能够得到较好的聚类效果,但对于不平衡数据的聚类效果不理想,往往会产生样本“均匀效应”,比如模糊c均值(FCM)[3]聚类算法在聚类过程中会均衡化各类别样本数量,使来自多数类中的部分样本被误划分到与其相邻的少数类中,造成很高的误分率。为了避免这个问题,一些学者对此提出了不同的解决思路,例如文献[4]提出了一种多聚类中心算法,通过将样本数量多的类别拆分为若干个类别来减弱不同类别之间的不平衡,避免“均匀效应”。但该算法只适用于不同类别特征之间有明显差异的场景,如果不同类别之间存在数据重叠现象则会产生不理想的聚类效果。Gustafson-Kessel (GK)算法[5]利用马氏距离代替了FCM目标函数中的欧式距离,考虑了除球形数据以外的其他簇形对聚类结果产生的影响。
针对以上问题,本文在D-S证据理论框架下提出一种不平衡数据多划分(Multi-partition,MP)聚类算法,并将其应用到建筑能耗异常检测中,构建MP算法能耗异常检测模型对建筑能耗中的异常值进行检测。实验表明,该算法能够有效避免样本“均匀效应”,极大降低误分率;通过对某商场建筑用电能耗异常值的检测,验证了MP算法能耗异常检测模型的有效性。
1 D-S证据理论概述
Dempster-Shafer(D-S)理论又称证据推理(Evidence Reasoning),1967年由Dempster最先提出[6],后由Shafer于1976年对其进行推广形成证据推理理论[7]。在Shafer模型中,定义了一个包含了有限个互斥且完备的元素集合Ω={ω1,ω2,…,ωn},Ω所有子集构成的集合称为Ω的幂集,表示为2Ω(包含2|Ω|个元素,其中|Ω|表示集合Ω中的元素个数)。例如,若辨识框架为Ω={ω1,ω2,ω3},则2Ω={φ,ω1,ω2,ω3,ω1∪ω2,ω1∪ω3,ω2∪ω3,Ω}(其中|Ω|=3,包含23=8个元素)。在Shafer模型中,从2Ω到[0,1]上的一个映射函数m()为一个证据的基本信任指派(basic belief assignment, bba),其满足以下条件:
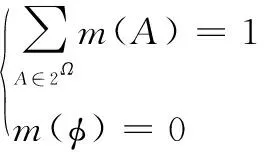
(1)
D-S理论将传统的辨识框架Ω扩展到幂集2Ω,使样本类别信息更加丰富(可以属于单类或由若干单类构成的复合类),其优势在于能够满足比概率理论更弱的条件并具有直接表达不确定的能力,因此在模式识别、信息融合领域得到了广泛应用。本文提出的MP聚类算法则基于D-S证据理论,引入复合类对不确定样本进行了合理表征。
2 不平衡数据多划分(MP)聚类算法
为了对不平衡数据进行有效聚类,避免样本“均匀效应”,本文提出一种基于D-S证据理论的不平衡数据多划分(Multi-partition,MP)聚类算法,能够有效处理不平衡数据集,合理表征处在不同类别边缘的不确定样本,极大降低误分率。该算法包含四个子步骤:数据集多划分、真实类别寻找、子数据集合并和剩余数据划分,下面将对MP算法的每个子步骤进行详细阐述。
2.1 数据集多划分
MP聚类算法的第一个步骤即对不平衡数据集中的样本进行子簇划分,受CCM算法[8]的启发,本节将提出一种改进的信任c均值(Improved credal c-means, ICCM)聚类算法,利用多聚类中心思想(生成多个子簇和若干个复合类,其中子簇个数N应大于数据集真实类别个数c,即N>c),对不平衡数据集中多数类和少数类中的样本数量重新进行平衡,从而有效降低错误率,避免“均匀效应”。由于复合类的引入,那些处在重叠区域的不确定样本能够被合理表征,且ICCM的计算复杂度远小于CCM。对于一个辨识框架为2Ω(Ω={ω1,…,ωN})的N类问题,ICCM算法分为以下两个部分。
1)子簇的划分:
在这部分中,不平衡数据集中的样本仅允许被划分到子簇和噪声类中,对于一个数据集X∈Rn×p,通过ICCM算法对目标函数的最小化将X划分为N个子簇,能够得到基本信任值M=(m1,…,mn)∈Rn×(N+1)和矩阵规模为N×p的聚类中心矩阵V,其中ICCM算法的目标函数JICCM被定义如下:
(2)
且需满足以下的约束条件:
(3)
其中:miφ表示样本属于噪声类的基本信任值mi(φ),1≤i≤n,1≤j≤N。参数β和δ的含义与CCM中参数的含义相同,其中δ用来控制噪声样本的数量,β为加权指数(默认值β=2)。目标函数JICCM最小化过程类似FCM和CCM,基本信任值m(.)通过以下公式更新:
(4)
其中:mij表示样本xi属于子簇ωj的基本信任值。
2)复合类的产生:
此过程通过设定复合类阈值计算得到复合类的基本信任值,对于样本xi,其可能所属的复合类Λi(Λi∈2Ω)被定义如下:
Λi={ωk∪,…,∪ωt|mi(ωk)-mi(ωt)≤ε},k≠t
(5)
且需满足:
mi(ωk)=max{mi(ω1),…,mi(ωN)},?1≤k,t≤N
(6)
其中:ε为可调节的复合类阈值,其值大小决定了划分到复合类中的样本数量。对于样本xi,其辨识框架拓展为Θi={φ,ω1,…,ωN,Λi},且不同样本可能得到不同的辨识框架Θ,复合类Λi的基本信任值m(Λi)被定义如下:
m(Λi)=mi(ωk)+,…,+mi(ωt)
(7)
样本xi通过以下公式对基本信任值m(.)归一化并进行更新:
(8)
其中:m(A)通过公式(4)计算可得,通过寻找基本信任值中的最大值,将样本xi划分到子簇或者复合类中,这样就可以得到经过ICCM划分后的子簇和复合类。
ICCM算法能够减小由于不同类别样本数量不等或分布不均对结果造成的影响,且能有效避免CCM“指数爆炸”现象,降低计算复杂度,实现数据的快速处理。在后面的步骤中,将利用子簇和复合类之间的密度关系对划分的子簇进行合并,所提密度合并规则仅允许复合类中所包含单类个数为2,即样本xi可能所属的复合类Λi在满足阈值ε的条件下仅能包含两个子簇。
复合类阈值ε的参数调整规则:在实际应用中,阈值ε需要被控制在一个合理范围之内,ε过大将使原本属于子簇的样本被划分到复合类中,导致不精确率增大;而ε过小则会导致复合类中的样本数量极少,极大增加误划分的风险。根据实验,建议阈值ε的取值范围为ε∈[0.1,0.3],默认值ε=0.2。
2.2 真实类别寻找
利用ICCM对不平衡数据集进行划分得到了N个子簇和若干个复合类,本节需要对数据集的真实类别个数进行确认,以确保子簇合并的正确性。受均值漂移(Mean-shift)算法[9]的启发,本节将提出一种基于K-NN的均值漂移(KNN-based mean shift, KMS)算法,利用K近邻(K-NN)思想计算当前样本点的均值漂移向量,使向量沿着密度增大的方向移动直到到达密度峰值处,自适应地确定数据集的真实类别个数c,克服传统均值漂移算法易受带宽h影响的缺点。当数据集分布不平衡时,固定带宽会影响聚类效果,KMS算法通过K近邻思想能够得到灵活的“带宽h”。具体的,使用一定数量的K个最近邻样本点对均值漂移向量进行直接迭代,这样不仅能够保证参与每次迭代的样本数量,而且可以很好适应迭代范围。样本的均值漂移向量Mh(x)被定义如下:
(9)
其中:Sh(x)和K分别表示样本x的集合和K近邻数量。在KMS中,仅改进Mh(x)以适应样本迭代范围,提高系统的鲁棒性,其他步骤与均值漂移算法相似。为了减小计算负担,这里仅取从ICCM算法中获得的N个子簇类中心作为均值漂移向量迭代的初始点,由 KMS的聚类结果可得到数据集的真实类别个数c。
参数K的选取原则:在实际应用中,N个子簇的类中心被用作迭代均值漂移向量的初始点,因此KMS算法对K值具有较强的鲁棒性。为了减少迭代次数,推荐K=(n/N)·(1±10%)作为默认值,其中n为不平衡数据集中包含的样本数量。
2.3 子数据集合并
本节将提出一种密度合并规则(Density- based merging rule, DMR),根据复合类和其所包含的两个子簇之间的密度关系对划分的子簇及部分复合类进行合并,直至得到与原始数据集真实类别个数相同的c个单类。复合类被认为是不同子簇之间的不确定类别,样本被划分到复合类意味着样本可能属于复合类所包含的子簇中的任何一个。如果ICCM将同属于一个类别的样本划分给了不同的子簇和复合类,表明这些子簇的密度可能非常相似;复合类中的样本通常分布在类别的相对中心,所以复合类的密度应大于或者介于复合类中所包含子簇的密度之间;如果复合类的密度小于其所包含的两个子簇的密度,则意味着这两个子簇属于不同的类别。综上,复合类和其包含的两个子簇之间存在以下三种密度关系:
C1:ρωk(ρωt)≤ρΛi
C2:ρωk(ρωt)<ρΛi<ρωt(ρωk)
C3:ρΛi<ρωk(ρωt)
满足上述C1和C2关系的复合类和子簇能够进行合并,并且满足C1关系的可优先合并。不难发现,子簇合并过程具有传递性,即如果有两个已部分合并的子数据集都与一个未合并的子簇满足密度合并关系,则这两个子数据集也应进行合并。目前已有许多密度计算方法得到了广泛应用,本节提供一种简单的方法对不同类簇Ai(子簇或复合类)进行密度估计,Ai的密度被定义如下:
氮肥品种均为尿素,磷肥品种为钙镁磷肥,钾肥为氯化钾,磷肥和钾肥均在蘖肥时全部施入稻田,施磷(P2O5)、钾(K2O)量均为62.5 kg/hm2。水稻采用人工收割,收割后种植蚕豆,无需施氮肥。
(10)
其中:ρAi为类簇Aj的密度,ni表示Ai中样本的数量,dij表示Ai中样本xi与数据集中样本xi的第j个近邻之间的欧式距离。这里利用K近邻思想来消除噪声带来的影响,默认值K=10。根据上述合并规则,能够将多划分获得的N个子簇以及部分复合类进行合并。
为了表示方便,定义ωk,tωk∪ωt,下面通过一个简单的例子来说明根据密度合并的过程。考虑一个真实类别c=2,多划分后子簇个数N=4的问题,各个子簇和复合类的密度分别为ρω1=0.56,ρω2=0.71,ρω3=0.47,ρω4=0.34,ρω1,2=0.24,ρω1,3=0.67,ρω1,4=0.21和ρω3,4=0.42。此例中各个子簇和部分复合类的具体合并过程如下:1)根据上述C1,可得Γ1=ω1∪ω3∪ω1,3;2)根据上述C2,可得Γ2=ω3∪ω4∪ω3,4;3)由传递性可得,ω1=Γ1∪Γ2∪ω1,4。因此,通过密度合并最终得到的新的类别结果如下:
ω1=ω1∪ω3∪ω4∪ω1,3∪ω3,4∪ω1,4;ω2=ω2
其中:Γi表示已合并的过渡簇(子数据集),ωi表示样本最终所属的真实类别。在获得需要的c个单类之后,可能仍会存在一些复合类(比如ω1,2)尚未合并,这些未合并复合类中的样本通常处于不同类别的重叠区域(例如ω1和ω2),因此需要采用更加谨慎的策略对这些样本进行划分。
2.4 剩余数据划分
本节提出一种剩余样本再划分规则(Re-partition rule, RPL)对未合并复合类中的样本进行再次划分以得到最终的聚类结果。未合并复合类中存在的少数样本经过再划分后仍很难被划分给某个特定类别,则这些样本将保留成为一个新的复合类,以降低误划分风险。RPL的关键在于,认为样本处在不同类别重叠区域的条件为该样本到不同类别中与其最近的K个近邻的平均距离无明显差异。对于未合并复合类中的样本xi,首先将获得xi在与此复合类相关的两个单类中的K近邻,定义样本xi到最终类别ωk的距离为xi到K个最近邻的平均距离,用公式表示如下:
(11)
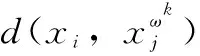
(12)
(13)
再划分参数χ的选取原则:χ∈[0,1]是一个可调的阈值参数,其值大小会影响最终复合类中的样本数量。χ越小,最终复合类中的不确定样本越少,这将会增加不确定样本误划分的风险;而随着χ增大,更多不确定样本被划入最终的复合类中,这将导致不精确率增高。χ应根据可接受的不精确程度进行调节。
为了更加清晰表达MP算法的基本流程和主要内容,图1展示了多划分(MP)聚类算法的流程框图。
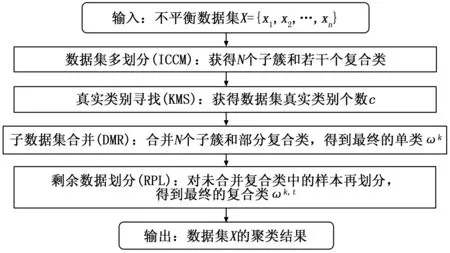
图1 不平衡数据多划分(MP)聚类算法流程框图
3 实验分析
本文利用UCI数据库[10]中五组真实数据集(即Wine、Bupa、Balancescale、Aggregation和WBC)对不平衡数据多划分(MP)聚类算法的性能进行测试和评价,通过与FCM、GK和CCM三种聚类算法对比验证MP算法的性能。Balancescale数据集共有3个类别,其中名为Left和Balanced的两个类别(分别包含288和49个样本)满足不平衡数据分布,选择这两类来评估算法性能。同样在Aggregation数据集中共有7个类别,选择其中分别包含102、34和34个样本的3个类别(即第三、五、七类)来验证算法的有效性。除以上两组数据集外,其余数据集均采用所有类别进行实验,实验所用数据集的详细信息如表1所示。
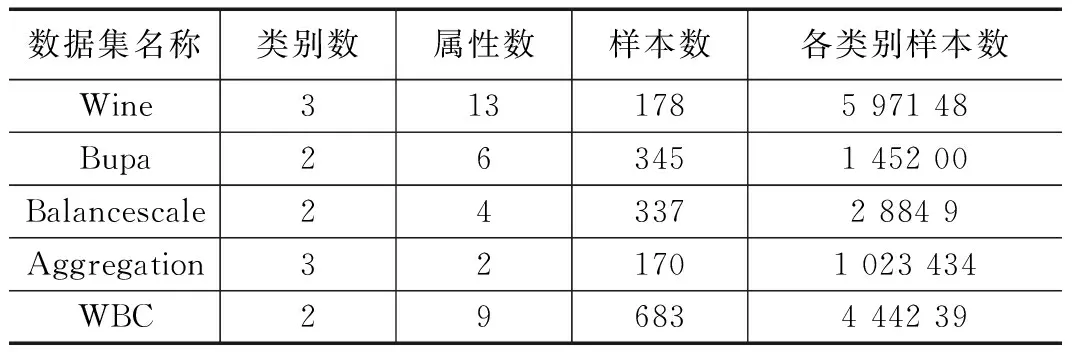
表1 实验所用五组UCI数据集详细信息
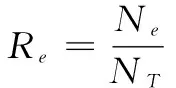

表2 五组UCI不平衡数据集聚类结果 %
从表2可以看出,MP算法对UCI中五组不平衡数据集的聚类结果均优于其他三种算法,错误率最低。MP算法中引入的复合类能从一定程度降低样本误划分的风险,合理表征处于重叠区域的不确定样本,降低错误率。从程序运行时间T上,FCM和GK算法由于没有复合类,故运行时间最快;CCM和MP算法由于引入了复合类,程序运行时间T会比前两种算法时间长,但通过实验数据可看出MP运行时间远小于CCM,说明MP计算复杂度远小于CCM,算法运行效率比较高。
4 MP算法在建筑能耗异常检测中的应用
4.1 MP算法能耗异常检测模型
本节将利用提出的MP聚类算法原理及内容构建能耗异常检测模型。MP聚类算法分为四个子步骤:数据集多划分、真实类别寻找、子数据集合并以及剩余样本划分,现将这些步骤运用在建筑能耗异常检测中,构建如图2所示的MP算法能耗异常检测模型。首先将预处理后的能耗数据集进行多划分,得到N个能耗子数据集(N>c)和若干个复合类;接着寻找数据集真实类别个数c,即正常能耗类别和异常能耗类别个数之和;然后对多划分得到的能耗子数据集和部分复合类进行合并;最后,对未合并复合类中的剩余能耗数据进行再划分,得到能耗数据集的类别划分结果,即最终的异常检测结果。从可行性的角度分析,由于能耗数据的分布符合聚类分布的特点,即距离类中心越近的地方样本点分布越密集,这就保证了MP算法在第三步密度合并时能够有效利用子数据集和复合类的密度进行子数据集合并,同时保证了MP算法能耗异常检测模型的可行性。
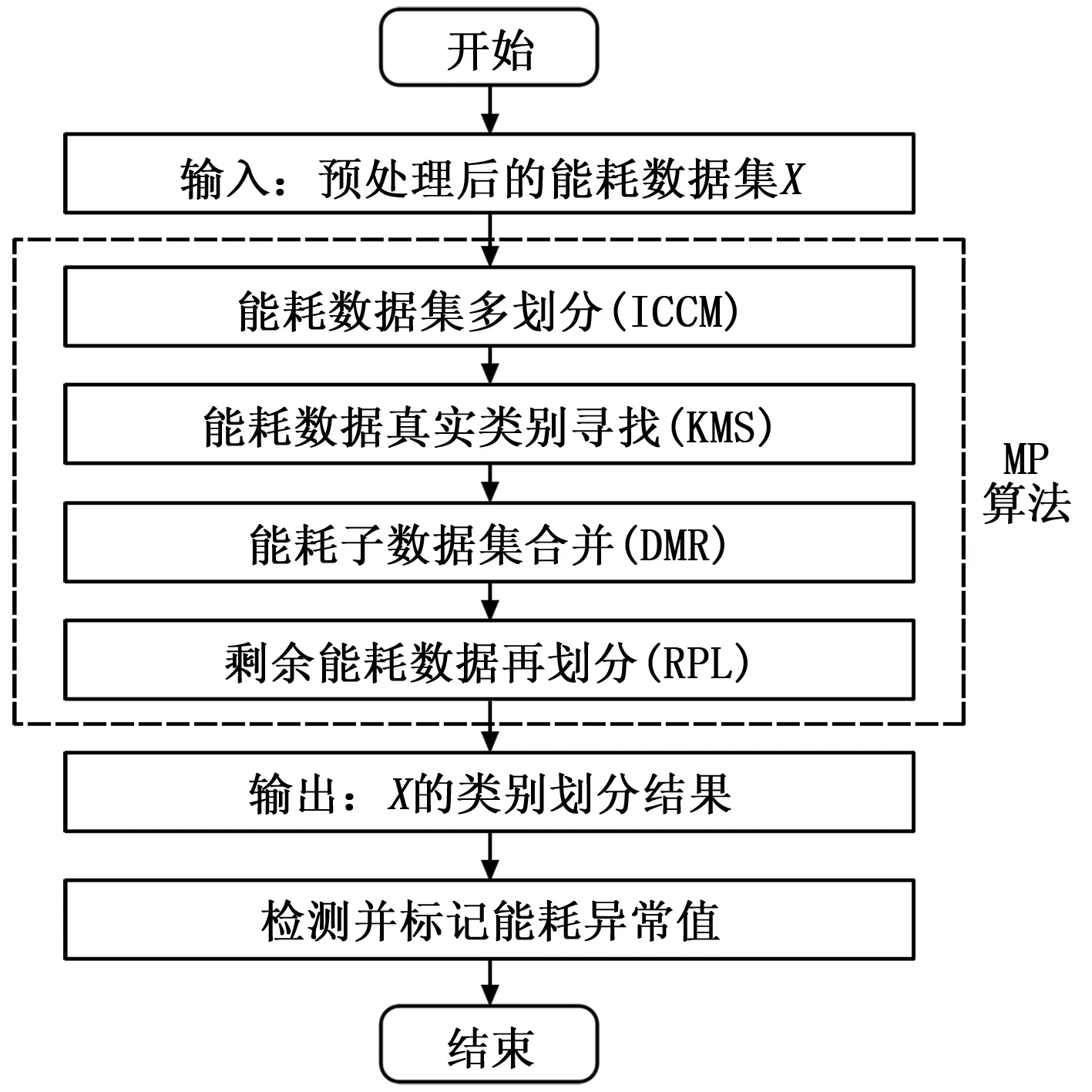
图2 MP算法能耗异常检测模型
4.2 能耗异常检测实验结果与分析
本文使用的能耗数据来源于对西安市某大型商场建筑的逐日分项用电监测,通过对该商场能耗监管系统进行调研,采集并记录了2018年3月5日至2019年2月28日的分项日用电能耗情况(共360组样本),包括空调、照明、动力、特殊设备用电量以及总用电量。选取该商场18年第二季度(6~8月,共计92天)日分项能耗(空调用电和照明用电)数据进行能耗数据异常检测实验,空调和照明用电能耗数据如图3所示。由于直接来源于现实生活中的数据经常会存在不完整、不一致等现象,这些对数据挖掘效果都会产生很大影响,因此在进行能耗异常检测实验前,需要对实验所用能耗数据进行预处理,确保数据的完整性和一致性。MP算法中的两个阈值分别设置为ε=0.2,χ=0.2。为了与MP算法得到的结果进行比较,实验还采用FCM和GK算法对相同用电能耗数据进行处理,得到了相应的聚类结果。

图3 西安某大型商场建筑18年第二季度(6~8月)空调与照明用电能耗数据
利用MP算法对上述用电能耗数据进行聚类,实验取N=8(即对该能耗数据集多划分得到的子数据集个数为8),图4 (a)和(b)分别展示了第二季度原始用电能耗数据以及MP算法对空调和照明用电能耗数据聚类得到的结果。

图4 MP算法建筑能耗异常检测实验结果
在实验过程中可得到能耗数据的真实类别个数c=3,从图4 (b)可以看出,MP算法将该季度用电能耗数据最终被划分为三类:ω1、ω2和ω3(等于能耗数据集真实类别个数),其中类别ω1从样本数量上看属于多数类,能够判断其属于正常能耗类别,其中的能耗数据在范围上相对比较稳定(即空调用电和照明用电量都在一定范围内);而类别ω2和类别ω3中所含能耗样本的数量很少(属于少数类),且分布上明显偏离类别ω1,故将这两个类别所包含的能耗数据认定为异常能耗数据,其中类别ω2中的能耗数据在空调用电量上表现出异常(远超出正常空调用电量水平),类别ω3中的能耗数据在空调用电和照明用电上均表现出异常(均远小于正常用电量水平)。从最终的聚类结果来看,能耗数据集除了被划分为以上三个类别外,还得到了两个复合类(ω1,2和ω1,3),它们所包含的能耗样本虽然不能认定为异常能耗数据,但介于正常与异常能耗之间,需要对这种不确定能耗数据采取更加谨慎的态度,以免导致数据误判的风险。图5为根据MP算法异常检测结果对异常能耗数据标记之后得到的用电能耗数据折线图(其中三角形和菱形标记分别表示检测出的空调用电异常能耗数据和不确定数据,圆形和正方形标记分别表示检测出的照明用电异常能耗数据和不确定数据),通过MP算法能耗异常检测模型,能够有效检测得到建筑能耗数据中的异常值,为建筑能耗监管系统的管理和运行提供必要的帮助,有利于管理人员及时发现并解决建筑中可能存在的问题与故障。
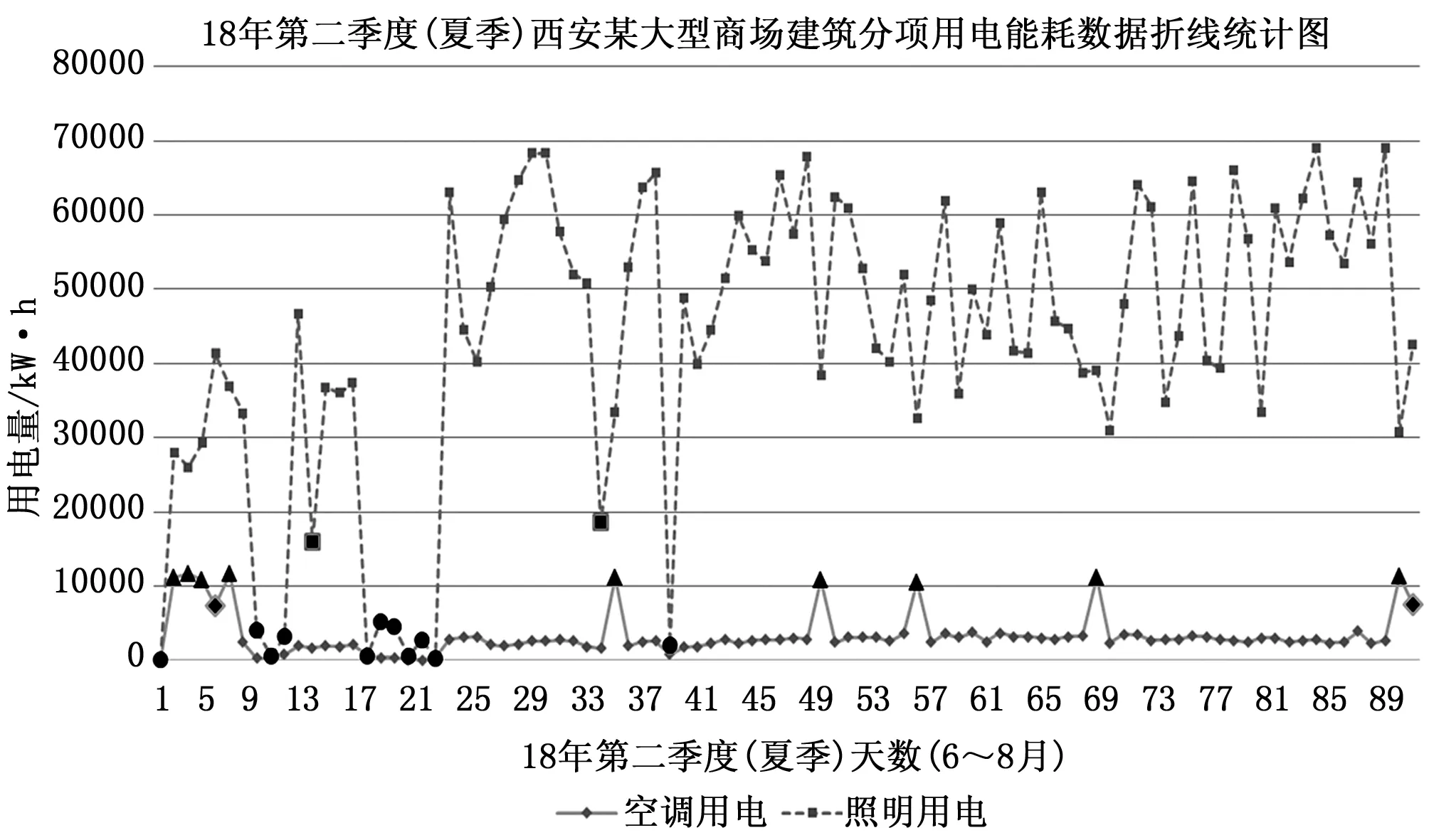
图5 空调/照明用电能耗异常检测数据图
为了与MP算法进行对比,采用FCM和GK两种算法对相同的能耗数据进行处理,图6 (a)和(b)分别为FCM和GK算法对用电能耗数据聚类的结果。由图6 (a)可看出,FCM将用电能耗数据划分为三类,但因其初始聚类时并没有类别先验信息,故在对数据进行聚类时首先需要获得数据的真实类别;从结果来看,FCM将MP算法中划分到复合类中的不确定数据强行划分到异常数据类别中,这样可能会增加数据误判为异常值的风险。从图6 (b)可以看到,GK将用电能耗数据划分为三类,但同样需要在聚类前对能耗数据的真实类别个数进行判断,最终的聚类结果显示,GK将原本属于正常能耗类别ω1中的部分数据错误划分到能耗异常类别ω2中,导致了部分正常能耗数据被误判为异常能耗,与MP聚类算法对比错误率明显增加。

图6 FCM和GK算法对第二季度用电能耗数据的聚类结果
5 结束语
由于异常能耗值在能耗数据中仅占很小的部分,能耗异常检测可以看作对不平衡数据的聚类,为了对不平衡数据进行有效聚类,避免样本“均匀效应”,本文提出了一种基于D-S证据理论的不平衡数据多划分(MP)聚类算法,并将其应用到建筑能耗异常检测中,构建了MP算法能耗异常检测模型对建筑能耗中的异常值进行检测。首先对预处理后的能耗数据集进行多划分,得到N个能耗子数据集和若干复合类;确定该能耗数据集的真实类别个数;然后对多划分得到的能耗子数据集和部分复合类进行合并;最后对未合并复合类中的剩余能耗数据进行再划分,得到能耗数据集的类别划分结果,即最终的异常检测结果。经UCI数据集验证,MP算法具有良好的聚类效果,通过对某商场建筑用电能耗数据进行能耗异常检测,验证了MP算法能耗异常检测模型的有效性。由能耗异常检测实验的结果可以看出,MP算法对于处在正常和异常能耗数据之间的不确定数据没有强行划分,但同时给算法带来了一定的不精确率,如何谨慎地对这些数据进行划分,从而确定这些能耗数据是否为异常值,是下一步需要深入研究的问题。

