深水安装缆轴向振动共振频率研究

佘振兴，罗晓兰，张 洁，刘军鹏，黄 枚

(1.中国石油大学(北京)机械与储运工程学院，北京 102249；2.中国石油大学(北京)海洋工程研究院，北京 102249； 3.惠生工程(中国)有限工程公司，上海 201210)①

水下生产系统是深海油气田开发工程中至关重要的一部分[1]。但在水下生产系统设施的下放安装过程中会出现安装缆绳断裂失效，导致水下设施安装失败，造成巨大的经济损失。因此，承受动态外界激励的安装缆绳轴向振动特性研究对深海安装系统的整体分析和工程设计十分必要。

Zhu[2]在缆绳三维动力响应方程中引入平均切向矢量法，采用外界激励为波高5 m、周期4 s情况下对缆绳进行了动力学仿真，研究成果对避免系统共振和延长缆绳寿命具有重要意义；Lueck R G等[3]利用傅里叶逆变换方法和小波法对垂向吊放系统频域模型进行求解，得出缆绳应力分布和缆绳末端的位移，将外界激励和船舶位移激励进行分析，可以对典型系统的瞬时应力和位移进行预测；Dantas C M S等[4-6]通过三角函数的逆变换，将简单边界下的物理模型确定的偏微分方程简化，使用等效替代方法将连续杆下端连接的重物等效为相同质量的附加杆，消除了复杂边界条件，有利于数值方法中计算的稳定性；张炜[7]在断开模式条件下，对深水钻井中立管的动态特性进行了研究，考虑了附加质量，建立了复杂边界条件的轴向振动连续杆模型，结合实例，利用试算的方法，求出共振前5阶固有频率和动态载荷；Wang等[8]研究了海洋钻井隔水管在安装时受到的轴向振动特性，建立了一个连续系统上端受到外界激励下端连接重物整体受到洋流阻尼力的物理模型，通过使用分离变量法求解相应的振动控制方程，得出相应的隔水管各个位置的动态振动响应。刘永林、朱克强等[9-10]对深海水下装备吊放系统缆索进行了研究，探索一种可描述缆索系统垂向吊放动力学行为的解析模型，给出它的自封闭方程、固有频率和简谐运动表达式；唐驾时[11]研究了一端带有集中质量，另一端连接弹簧情况下杆的轴向振动问题，用摄动法求具有非线性边界条件的非线性偏微分方程的近似解析解；M Shatalova[12]考虑在简单边界条件下经受纵向振动的经典粘弹性杆的长度是可随时间而变化的，推导出杆的动力学的新偏微分方程；Cveticanin L[13]提出了一种用于强非线性粘着杆的轴向振动频率和周期的计算方法，利用变量分离的方法，建立了特殊初始条件下的方程解，将偏微分方程分为两个非线性强非线性二阶微分方程。

1 理论模型

在深海下放安装作业过程中，安装缆绳具有连续分布的质量与弹性，且在任意截面形变量微小，满足连续条件。假设安装缆绳各个截面受力均匀并且各向同性，它可以被看成是一个连续系统的轴向振动问题，通过求导出控制运动偏微分方程。结合边界条件求解，可以解出连续系统的轴向振动响应特性[14]。

缆绳的轴向振动特性符合连续杆轴向振动系统的条件，因此安装缆绳下放安装管汇的实际物理模型如图1所示，安装缆绳上端承受的升沉运动作为一个外界激励FH作用在缆绳上端，缆绳承受的海水阻尼力简化为弹簧FC，下端连接重物承受的拖曳力简化为弹簧力FD，缆绳长为L，缆绳质量为m，下放物体湿重为M，缆绳轴向刚度为EA，固有频率为ω0，共振频率为ωn。对于这种承受复杂边界条件、外界激励以及非线性阻尼力的连续杆系统的轴向振动响应特性研究，首先需要求解出简化系统的固有频率，然后考虑承受外界激励以及海水阻尼力，求解系统的共振频率，如图1所示。

图1 安装缆绳轴向振动分解示意

2.1 安装缆绳轴向振动固有频率

缆绳下放安装系统的自由振动特性需要考虑到缆绳的质量、密度、弹性模量、长度及下放物体带来的复杂边界条件的影响。建立缆绳下放安装系统自由振动的物理模型如图2a，其中u是轴向形变位移，du/dx是轴向应变。

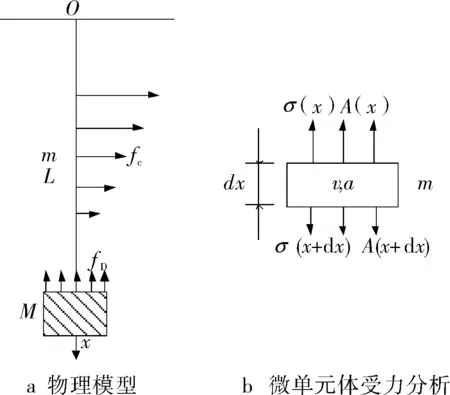
图2 自由振动物理模型受力分析

取缆绳上质量为m的任意微单元体dx进行轴向受力分析，如图2b所示。微单元体上端轴向力为：

(1)

忽略高阶分量的影响，微单元体下端轴向力为：

(2)

式中：E为缆绳材料的弹性模量，Pa；A(x)为缆绳在x处的横截面积，m2。

对微单元体进行受力分析，可得缆绳轴向无阻尼自由振动微分方程为：

(3)

式(3)可以简化为波动方程。

(4)

(5)

结合缆绳受力情况分析，初始条件和整体的边界条件方程为：

(6)

式中：L为缆绳长度，m；M为下放物体湿重，t。

对于波动方程(5)使用分离变量法求解[15]，可得：

(7)

式中：A，B，C，D为参数；ω为频率。

由边界条件方程(6)与式(7)，可得：

(8)

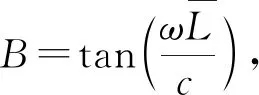
(9)

将式(9)代入式(7)得：

(10)

轴向力表达式为：

(11)

缆绳顶部(x=0)处动态应力为：

(12)

(13)

对应固有周期T为：

(14)

2.2 安装缆绳轴向振动共振频率

建立安装缆绳阻尼受迫振动模型及缆绳中一个微单元体dx的受力分析，如图3。其中f(x，t)表示微单元体dx上作用的外力。

图3 阻尼受迫振动模型受力分析

根据达朗贝尔原理，缆绳轴向受迫振动微分控制方程为：

(15)

式中：H为单位长度的线性阻尼系数，kg/(m/s)；ρ(x)为缆绳在x处的密度，kg/m3。

假设缆绳各向同性且横截面积保持一致，式(15)可简化为安装缆绳的阻尼轴向受迫振动微分控制方程。

(16)

设H/m=2h，而m=ρA，则：

(17)

缆绳的上端固定在安装船的绞车上，跟随安装船做升沉运动。缆绳的下端连接着设备，可以看成是连接着集中质量、拖曳力。阻尼轴向受迫振动微分控制方程的边界条件为：

(18)

式中：ρs为海水的密度，kg/m3；CDZ为下放物体的垂直拖曳力系数；AP为下放物体在垂直方向有效受力面积，m2；ηL为缆绳运动幅值，m。

缆绳带阻尼振动微分方程的解为：

(19)

式中：φi(x)为缆绳轴向阻尼振动的振动模态函数。

φi(x)振动模态函数满足下列条件。

(20)

由式(17)、式(19)，可以得到一个微分方程：

(21)

由于振动模态的正交性，式(21)可表示为：

(22)

对式(22)常系数微分方程进行求解。

安装轴向振动特性函数为：

(23)

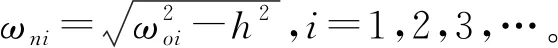
2.3 案例分析

以一个实际深海管汇下放安装作业为例，水深为1 500 m，缆绳直径100 mm，钢缆的弹性模量0.85×1011N/m2，海水密度取1 025 kg/m3，下放设施湿重为190 t，阻尼系数取0.02，且下放物体在竖直方向投影面积为10 m2，外界激励振幅和周期分别是1 m和8 s。

缆绳直径为100 mm钢丝缆绳单位长度干重为469.03 N/m，单位长度湿重为390.14 N/m，破坏强度为6 333.58 kN。计算可得安装缆绳参数如表1。

表1 安装缆绳参数

从表1中可知，在该安装工况下，阻尼系数为0.4 kg/(m/s)，第1阶固有频率和共振频率分别是4.238 8 Hz和4.219 8 Hz，降低了0.4%，影响很小。工程应用中，在小阻尼的结构系统的振动问题，通常可以用固有频率代替共振频率。

3 敏感性分析

为了考虑实际安装工况中，不同安装水深、缆绳直径及水下生产系统设施湿重对安装缆绳共振频率的影响，以深海管汇下放安装作业实例为基础，研究了不同水深、缆绳直径和下放重物质量对安装缆绳前4阶共振频率的影响，并对3种影响因素进行敏感性分析。

3.1 水深对共振频率的影响

在下放深度为500、1 000、1 500、2 000、2 500 m 5种情况下，保持其他参数不变，安装缆绳共振频率的变化趋势如图4所示。

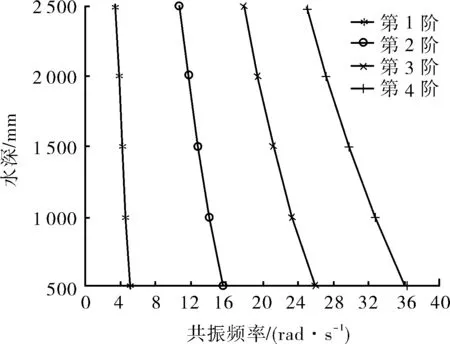
图4 不同水深下安装缆绳前4阶共振频率

由图4可知，安装缆绳的前4阶共振频率随着下放水深的增加而逐渐减少。其中，第4阶共振频率的变化斜率从最大36.309 4 rad/s(水深500 m)减少到25.085 2 rad/s(水深2 500 m)；最重要的第1阶共振频率从5.185 7 rad/s(水深500 m)减少到3.581 7 rad/s(水深2 500 m)，因为基频引起的振幅更大、更容易使缆绳断裂失效，在实际安装工程获得更多的关注。因此，在不同的安装水深下，当外界激励频率为3.5 ～ 5.0 rad/s时，需要对安装缆顶端采取保护措施，或者考虑中止安装作业，避免缆绳断裂。

3.2 缆绳直径对共振频率的影响

在缆绳直径为80、90、100、110、120 mm 5种情况下，保持其他参数不变，安装缆绳的共振频率如图5。

由图5可知，安装缆绳的前4阶共振频率随着缆绳直径的增加而逐渐增加。其中，第4阶共振频率的变化斜率从最大26.336 9 rad/s(直径80 mm)增加31.772 0 rad/s(直径120 mm)；最重要的第一阶共振频率从3.759 6 rad/s(直径80 mm)增加到4.537 8 rad/s(直径120 mm)，变化不大。因此，安装缆绳的直径变化对共振频率的影响不大；当外界激励频率为3.75～4.55 rad/s时，需要注意共振现象的发生。

图5 不同缆绳直径下安装缆绳前4阶共振频率

3.3 下放设施湿重对共振频率的影响

在下放设施湿重为90、140、190、240、290 t 5种情况下，保持其他参数不变，安装缆绳的共振频率如图6。

图6 不同下放设施湿重下安装缆绳前4阶共振频率

由图6可知，安装缆绳的前4阶共振频率随着下放设施湿重的增加而急剧减小。其中第4阶共振频率的变化斜率从最大48.010 9 rad/s(90 t)减小到21.469 9 rad/s(290 t)；最重要的第1阶共振频率从6.857 7 rad/s增加到3.064 9 rad/s，变化明显。因此，下放设施湿重对安装缆绳的共振频率影响很大，在实际安装工况中，下放不同的物体质量时需要对安装缆绳的共振频率和外界激励频率做出更多的关注。为了避免共振现象的发生，在安装大质量设施时，应选取更粗的缆绳，以提高共振频率值。

3.4 敏感性分析

选取水深1 500 m，缆绳直径100 mm，下放设施湿重190 t为标准组，结合3种因素对共振频率影响，绘制不同因素的敏感性分析曲线如图7。

图7 不同因素的敏感性分析曲线

由图7可以看出，下放设施湿重曲线的斜率最大，缆绳直径曲线的斜率次之，水深曲线的斜率最小。说明安装缆绳的共振频率受下放物体质量的影响更大，根本原因在于下放设施的湿重大于缆绳的质量，对缆绳下放系统的共振频率影响很大。所以，在使用缆绳下放安装时，需要根据下放位置海况，对下放物体质量进行调配，避免波浪频率接近安装缆绳共振频率。

4 结论

1) 通过安装缆绳的受力分析，运用特殊的函数变换，结合海水弱阻尼性质，求解出安装缆绳共振频率跟固有频率的关系；对弱阻尼系统下安装缆绳轴向振动的共振频率和固有频率进行比较，得出在弱阻尼情况下共振频率可以用固有频率表示。

2) 对下放水深、缆绳直径和下放设施质量3个因素进行敏感性分析，得出对安装缆绳轴向振动共振频率影响最大的是下放设施湿重，影响最小的下放水深。