南海某油田防沉板极限承载力研究

李书兆，贾 鹏，尹 丰，张 宁，石 磊，刘 璞，庞 楠

(1.中海油研究总院有限责任公司，北京 100028； 2.哈尔滨工程大学 机电工程学院，哈尔滨 150001；3.海洋石油工程股份有限公司，天津 300451)①

随着海上油气资源的开发逐渐转向深水，水下生产系统以其建设周期短、成本低和抵抗自然灾害能力强的优势逐渐成为深水油气资源开发的主流模式[1]。水下生产系统基础结构的研究，是水下生产系统各方面研究中最基本的部分，对水下生产系统各设备的结构设计、安装方式以及稳定性有着重要影响。

常见的水下生产系统的基础形式有防沉板、桩基础以及吸力桩3种[2]。防沉板基础以其结构简单、造价低廉、性能可靠和安装方便的特点，被广泛用作水下生产系统各设备的基础结构。使用防沉板作为其基础结构的水下设备有水下管汇、管道终端、管汇终端、水下脐带缆分配单元等，同时，一些临时的水下维修设备也常采用防沉板基础。

早期研究防沉板的极限承载力时，主要借鉴了Prandtl、Meyerhof、Hansen等人对陆上浅基础极限承载力计算的半经验、半理论方法，美国石油协会结合这些理论发布了API RP 2A和API RP 2GEO等行业设计规范。Randolph等[3]采用破坏包络线的方法，研究了复合加载情况下带裙边条形基础和圆形基础的承载特性，发现两种基础在复合载荷下其承载特性随基础形状和土体抗剪强度变化而变化。刘润等[4]针对饱和软黏土中不同形状的防沉板，采用数值模拟方法确定了V、H、M、T联合作用下的地基承载力包络线，得到了各种载荷占据主导位置时的防沉板形状最优方案。徐蒙[5]运用Abaqus软件，通过CEL方法研究了不同结构防沉板下部结构贯入土体的过程，研究结果显示地基土的隆起严重影响了防沉板的贯入过程。上述研究多集中于不同构型复合加载下的承载特性，研究结果局限性较强，应用于南海某油田实际工况时的计算结果误差大。本文考虑该油田实际工况条件，结合规范计算方法和有限元仿真技术，研究了防沉板的极限承载力。

a 矩形基础

b 圆形基础

1 防沉板极限承载力标准计算方法

防沉板基础埋置深度一般小于其横向最小尺寸，通常被认为是一种浅基础。在防沉板的设计工作中，必须保证下部土体能够承受防沉板及上部结构整体的结构载荷而不发生剪切破坏。

在防沉板的稳定性评估中，必须考虑连接管道对其作用力、拖网力、安装海域的环境条件(例如波、浪、流)、土壤设计数据和结构自身的重力等[6]。对于指定水下设备，防沉板的尺寸主要取决于海洋工程地质调查中土的强度指标。防沉板的稳定性评估中应考虑：①稳定性。包括极限承载力、抗滑移能力等；②沉降值。要求防沉板基础及上部结构安装在海床后，不能有太大的沉降，以免对其它连接部件造成附加应力。

极限承载力计算公式是根据极限平衡的基本原理推导出来的。影响防沉板基础极限承载力的因素有很多，除了土体的性质以外，还与防沉板的形状、尺寸和所受载荷等。根据实际安装环境土壤的具体情况及API规范[7]，对防沉板极限承载力的计算主要考虑3种情况。

1) 不排水承载能力——抗剪强度不随深度增加时。

如果基础下部深度至少在基础宽度2/3的范围内，土壤的不排水抗剪强度近似恒定时，可将基础下部的土壤的不排水抗剪强度看作为恒定值。这种情况下，防沉板基础的极限承载力为：

Qd=(suNcKc)A′

(1)

式中：Qd为基础破坏时的最大竖向载荷；su为土的不排水抗剪强度；Nc为无量纲常数，取值5.14；A′为取决于载荷偏心度的基础有效面积；Kc为考虑载荷倾斜度、基础形状、埋置深度、基底倾斜度和泥面倾斜度的修正系数。

2) 不排水承载能力——抗剪强度随深度线性增加时。

海底沉积物可以自然地显示出随深度增加的不排水抗剪强度。不排水条件下，如果抗剪强度随深度线性增加，则防沉板基础极限承载力为：

(2)

式中：F为与κB′/suo有关的修正系数；κ为不排水抗剪强度线性增长梯度；suo为基础底面土的不排水抗剪强度，B′为基础最小有效横向尺寸。

3) 排水承载能力

排水条件下，防沉板基础极限承载力为：

(3)

其中:

Nr=1.5(Nq-1)tanφ′。

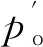
图1 推荐的承载能力系数

根据对目标油田的环境调查，土壤抗剪强度在泥线以下基础宽度范围内近似恒定，因此在计算极限承载力时，选用不排水条件下土壤抗剪强度恒定的情况。

2 参数选取及极限承载力计算

2.1 有效面积

载荷偏心减小了基础能承受的极限垂直载荷，需予以考虑[8]。图2为具有偏心载荷的基础，偏心e是从基础中心到合力作用点的距离，按平行于土壤-基础接触面来度量。合力作用点是折减后面积的形心，偏心距e=M/Q，M是倾覆力矩，Q是垂直载荷[9]。

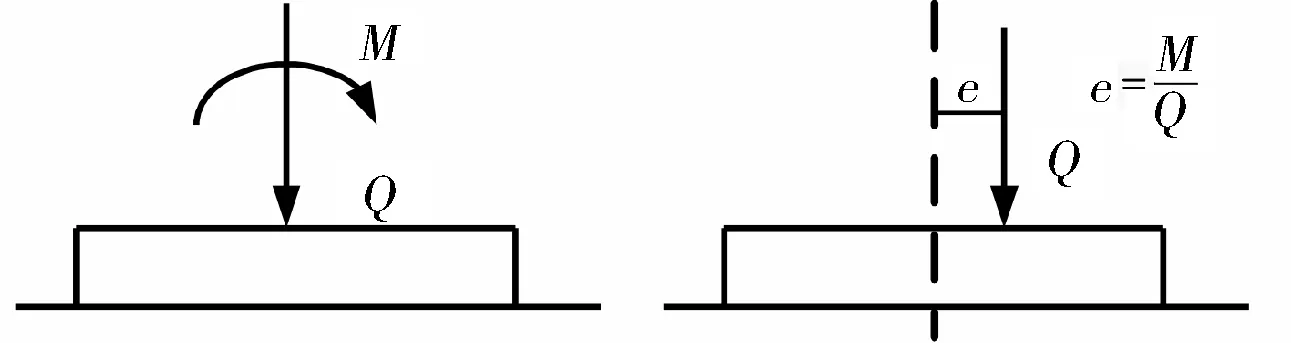
图2 偏心载荷基础的等效载荷

对于矩形基础，偏心可以相对于基础的任一轴出现(如图3)。基础减少的尺寸为：

L′=L-2e1

B′=B-2e2

(4)

A′=B′L′

式中：e1为沿长度方向的偏心距；e2为沿宽度方向的偏心距；L′为防沉板的有效长度；B′为防沉板的有效宽度。

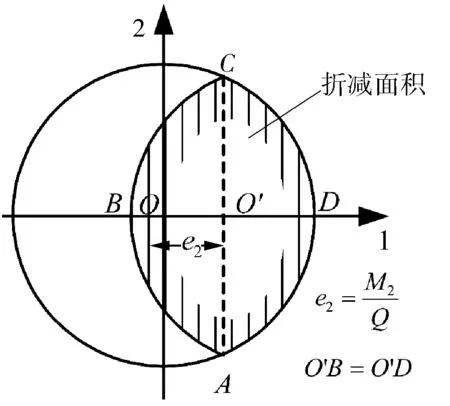
对于半径为R的圆形基础，有效面积的形心是将基础中心移动一个距离e2得到的。因而有效面积被认为是扇形ADC的面积的2倍。另外，其有效尺度也被认为是长宽比等于直线长度AC与BD比的矩形。其有效尺寸为：

(5)

其中：

(6)

2.2 修正系数Kc

系数Kc是考虑在安装环境时，对各部分载荷的修正系数[7]。对于系数Kc，不排水条件下，当土体的抗剪强度不随深度变化时，按式(7)计算。

Kc=1+sc+dc-ic-bc-gc

(7)

其中：

sc=0.18(1-2ic)(B′/L′)

dc=0.3arctan(D/B′)

(8)

bc=2v/(π+2)≈0.4v

gc=2β/(π+2)≈0.4β

式中：sc、dc、ic、bc和gc分别为与基础形状，埋置深度，载荷倾斜，基础倾斜和海床表面倾斜有关的修正系数。

基础和海床表面倾斜角度如图4所示。

图4 防沉板基础位置参数

2.3 极限承载力计算

我国南海某油田水深430 m，采用管汇+丛式井的水下生产系统。水下生产系统主要由管汇、采油树、水下分配单元、水下电力分配单元等组成。

某设备的基础形式采用防沉板结构，如图5所示。防沉板设计有吊点和各设备的固定点，设备一般采用对称布置，使其重心位置靠近防沉板形心位置[10]。其在水下安装时通过装置进行调平，无埋深。因此，认为其有效面积等于其正常面积，并且修正系数Kc等于1。

图5 南海某油田防沉板结构示意

根据油田实际土壤环境，防沉板采用带裙板的形式，其目的为防止海流的冲刷影响[11]，此防沉板设计时不考虑裙板对极限承载能力的影响。为了便于回收，防沉板采用开孔形式。防沉板结构尺寸为21 m×7.5 m，裙板高0.3 m，厚度为10 mm。

根据工作海域土壤调查结果，土壤参数如表1所示。

表1 工作海域土壤参数

将各参数代入式(1)，得:

Qd=(suNcKc)A′=8.1×106N

由计算结果可知，防沉板的极限承载力为8.1×106N。

3 防沉板极限承载力有限元仿真

3.1 建立有限元模型

裙板设置的目的为抵抗海流冲刷，同时增加抗滑移能力，在设计过程中可忽视其对极限承载力的影响。在基于Abaqus对防沉板的承载能力进行分析的过程中，忽略次要特征，将防沉板简化为平板模型。

由于极限承载力为本次分析的重点，故海洋土的本构关系采用Mohr-Coulomb模型[12]。在数值模型中，防沉板和土体均采用8节点6面体缩减积分单元(C3D8R)。在防沉板底部中心位置设置参考点，并将其与防沉板的所有外表面进行运动耦合(Coupling-Kinematic)。为了尽量消除仿真过程中边界效应的影响，土体模型尺寸设为105 m×37.5 m×22.5 m。防沉板底部与土体的切向接触设置为粗糙接触(Rough)，法向接触为硬接触(Hard)，并选择接触后不允许分离。防沉板和土体的模型如图6所示。

图6 防沉板-土体有限元模型

3.2 采用位移控制法求极限承载力

在模拟防沉板与土体的相互作用之前，对土地进行地应力平衡[13]。设置“地应力平衡”分析步，并在此分析步中将防沉板模型设置为未激活状态。计算完成后，土体的Mises应力分布和位移分布如图7～8所示。

图7 地应力平衡-Mises应力分布

图8 地应力平衡-位移分布

根据地应力平衡结果，土体的应力与位移沿竖直方向均匀分布，这是与实际情况是相符的，在此基础上分析防沉板的极限承载力。

采用位移控制法，对防沉板底面施加一个向下的竖向位移，并且限定水平位移为0[14]。Abaqus软件计算结果的等效塑性应变(PEEQ)和Mises应力分布视图显示了基础底部土体破坏的过程，如图9～10所示。

从图9～10可以看出，在采用位移控制法过程中，对防沉板施加竖向位移时，其端部土体首先形成塑性区域，形成局部剪切破坏，随之塑性区域逐渐扩大。当竖向位移继续增加时，塑性区域完全贯通，此时对应的载荷为极限载荷。此后，土体的变形趋势突然增加，地表在防沉板四周呈隆起状态，基础底部土体已完全破坏。

图9 防沉板底部土体破坏过程

通过提取防沉板基础底部参考点的位移和约束反力，并将其拟合为一条曲线，此曲线即为位移控制法下获得的防沉板载荷-位移曲线，如图11所示。通过载荷-位移曲线可以看出，防沉板在竖向位移0.15 m时达到拐点，此时对应的载荷即为极限载荷，约为8.0×106N。与采用标准公式计算出的极限承载力8.1×106N相比，有限元分析得到的极限承载力小1.23%，说明通过规范计算和通过有限元仿真求出的极限承载力是基本相符的。

图10 竖向位移下土体Mises应力分布

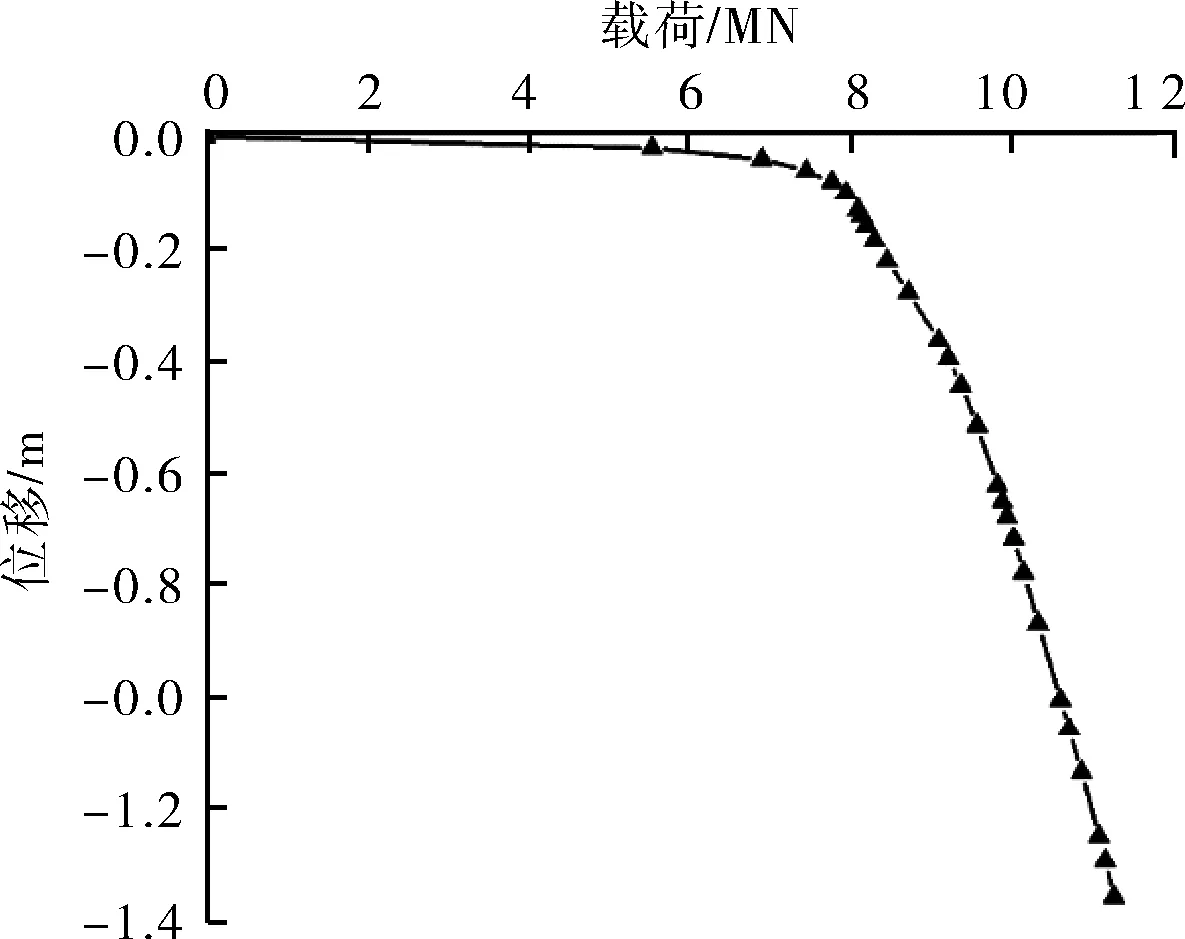
图11 防沉板载荷-位移曲线

4 结论

1) 研究了3种不同安装环境下防沉板极限承载力的计算式及参数的选取。计算得到南海某油田防沉板实际工况条件下的极限承载力为8.1×106N。

2) 使用Abaqus软件建立了防沉板与土体的有限元模型，结合实际环境参数，得到了防沉板的位移-载荷曲线，采用有限元仿真求得南海某油田防沉板极限承载力为8.0×106N。2种结果对比相差1.23%。

3) 有限元仿真结果显示，防沉板下部土体在上部载荷作用下，首先在端部形成塑性区域，随之塑性区域逐渐扩大并形成贯通趋势，达到极限载荷，此后土体变形突然加大，并形成隆起状态。