基于鲁棒滑模策略的伺服电机改进内模控制

陈凯镔，徐 俊，陶沙沙，王从明，余 冬

(1.成都工业职业技术学院 汽车工程学院,成都 610000；2.西安交通大学 机械工程学院，西安 710038；3.成都石化工业学校，成都 610000)

0 引 言

伺服电机因其高效、高性能、低噪声、高功率和大转矩等优点在工业、航空航天、汽车等领域中得到了广泛的应用[1-2]。学者不断地探索着更先进的控制理论，以期实现伺服系统的高精度控制，但是其恶劣的工作环境以及机械结构建模的不确定性使得伺服电机的高精度控制一直存在问题[3-4]。

内模控制(Internal Model Control,IMC)为分析和设计控制系统提供了一个有效、直观、简单的框架,因此在电机控制中应用广泛[5]。文献[6]针对永磁同步电动机调速系统，提出了一种模糊自适应内模控制策略；文献[7]中提出了一种基于神经网络逆系统结合内模控制器的新型控制方案；文献[8]在2自由度内模控制(2 Degree of Freedom,2DOF-IMC)策略中引入了一种免疫算法来实现异步电机的运动控制等，但是上述文章设计的控制器性能依赖于参数与先验知识，使得控制性能具有一定保守性，此外，还有一些参数需要在线调整，为了保证自适应律的收敛性还需更多的处理，这增加了其工程应用的难度。

滑模变结构控制(Sliding Mode Control,SMC)利用边界条件可以获得较好的鲁棒性，从而获得较高的跟踪精度[9]。这种控制方法已广泛应用于实际工程中，如伺服电机控制[10]、电液控制[11]、机器人控制[12]等。然而，要得到更好的跟踪性能，必须抑制抖振。但是由于实际的系统中存在着有限的切换频率和未建模动态，若通过边界层解减弱其抖振，这可能会导致存在恒定干扰时产生稳态误差，使得控制精度下降。

综合上文所提到的控制策略缺点，通过借鉴了内模控制原理和滑模控制理论，提出了一种基于鲁棒滑模控制律的2自由度增强型内模控制器，用于伺服电机在模型不确定性和外界干扰下的的高性能运动控制。不同于之前所提到的将内模控制主要用于预测的策略，该控制策略是通过SMC结构对基于IMC的控制器的控制性能进行分析，并利用基于SMC方法的鲁棒控制律处理基于IMC控制器的鲁棒性问题。为了解决稳态误差问题，在新型控制架构中引入了基于2DOF-IMC结构的增强型IMC策略，来进一步提高其控制性能。

1 系统建模

伺服系统主要包括交流伺服电机和直接驱动惯性负载的伺服驱动器。该系统惯性荷载的动力方程为

(1)

式中,θ为系统输出的角位移，J为惯性负载，B为粘滞摩擦系数，u为控制输入转矩、D(t)为未建模干扰，如外部干扰和未建模动态。将式(1)转换为状态空间模型为

(2)

式中,x1和x2为系统状态变量，分别表示角位移和速度，φ=[φ1,φ2]T=[1/J,B/J]T为系数向量，d(t)=D(t)/J为扰动。根据文献[13]做出以下假设：

假设1.参数不确定性的边界已知，即：

φ∈Ωφ,{φ:φmin≤φ≤φmax}

(3)

假设2.未知干扰d(t)的边界为

‖d(t)‖≤dmax<+∞

(4)

其中,dmax已知。

2 控制器设计

2.1 基于IMC的标准控制器设计

由式(1)可得伺服系统的传递函数为

(5)

式中，Jn和Bn分别为参数J和B的标称值，Gn(s)为过程的标称模型。本文选取的IMC滤波器为

f(s)=1/(λs+1)

(6)

IMC滤波器f(s)用于实现特定跟踪。其中λ为IMC滤波器的时间常数。基于标准IMC的PD控制器可以表示为[14]

(7)

其中,kp=Bn/λ和kD=Jn/Bn分别为比例系数和微分系数。相应的输出可以表示为

(8)

其中,R为参考轨迹。考虑到R(s)=0，D=0的调节器情况，假设G(s)=Gn(s)，则输出可表示为

(9)

由式(9)可知，在输入扰动为常数时，跟踪响应存在稳态误差，不能保证系统控制要求。

2.2 基于SMC的鲁棒SIMC-PD控制器设计

鲁棒滑模控制结合标准内模控制(Standard Internal Model Controller,SIMC)的控制结构如图1所示，该控制器可表示为

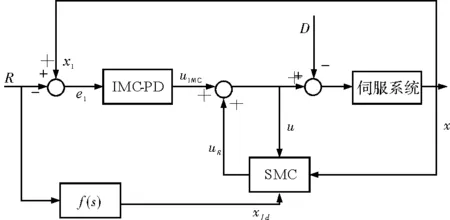
图1 SMC-SIMC-PD控制器的结构

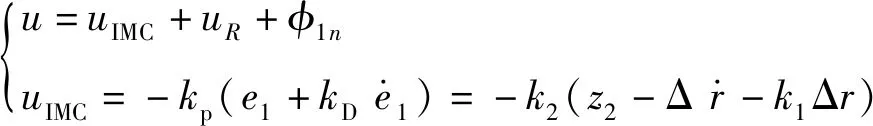
(10)

其中,uIMC为从SIMC-PD控制器式(7)中推导出来的线性反馈控制律，k1=Bn/Jn和k2=Jn/λ为反馈增益，uR为鲁棒控制律，用于减小模型误差或外部干扰的影响。

选择uR作为滑模面切换函数，即uR=-α×sign(z2)。然而，这种不连续的控制规律会导致抖振，从而导致跟踪性能不够理想。为了减小抖振，提出了一种连续鲁棒反馈线性化控制器。考虑到假设1和假设2，存在满足以下条件的uR：

z2uR≤0

(11)

(12)

(13)

满足约束(11)和约束(12)的uR的设计方法可以参考文献[14-15]。例如令g为任何符合的平滑函数

g≥‖φM‖‖φ‖+dmax

(14)

其中，φM=φmax+φmin。然后，给出了一个满足式(11)和式(12)的平滑例子：

uR=-g2z2/(4ε)

(15)

当存在不确定性和扰动时，所提出的SIMC-PD-SMC策略能够实现预设的输出跟踪性能，并保证较好的跟踪精度。但是由于在控制策略中考虑了不确定界限，此时鲁棒控制器(15)相当于一种高增益反馈控制律，过小的 值意味着控制器高的带宽，这可能会导致不稳定。为了避免这个问题，必须对ε值进行限定，然而这样只能保证原点附近的稳定性。

2.3 基于SMC方法的2DOF-IMC的控制器设计

为了进一步提高鲁棒性和稳定范围，提出了一种结合鲁棒滑模控制律的2自由度增强型IMC控制器。在2DOF-IMC策略中，IMC滤波器可以表达为[16]

fD(s)=(1+2λs)/(λs+1)2

(16)

为了保证系统在输入扰动恒定的情况下达到零稳态误差，必须满足以下条件

(17)

令基于2DOF-IMC的控制器为

(18)

为保证系统能达到相同的指定跟踪性能，采用定点滤波器F(s)，如下所示：

(19)

然后，设置滤波参考轨迹RF为

RF(s)=F(s)R(s)

(20)

定义控制输入误差E1=x1-RF，则有：

E1=z1-ΔR;ΔR=RF-x1d

(21)

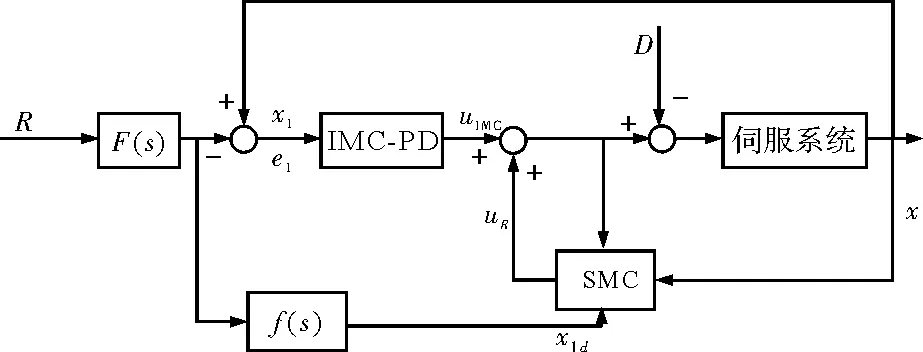
图2 2DOF-IMC-SMC控制器的结构

基于滑模理论的2自由度增强型内模控制器结构如图2所示，相应的控制律为

(22)

式中，ka、kb、kc为正反馈增益，可从2DOF-IMC-PID控制器(18)中获得：

(23)

定义另一个跟踪误差函数为

(24)

从p2到z1的传递函数可以表示为

(25)

由于Gp(s)是渐进稳定的，所以p2收敛到零意味着使z1也收敛到零。

联立式(24)以及式(21)～式(23)，可以得到p2的动力学表达式为

(26)

考虑到假设1和假设2，同样存在满足以下条件的uR：

p2uR≤0

(27)

(28)

定理1：假设期望轨迹是二阶连续可微分的，而且所提出的控制律(22)能够保证伺服系统有界。此时，李亚普诺夫函数Vt可以表示为

(29)

上式满足：

(30)

证明：

联立式(6)、式(9)、式(19)、式(20)可得：

(31)

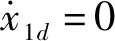
(32)

对式(32)积分，可得：

(33)

当kb=1/(2λ)时，则有：

(34)

当ka=φ2n时，则有

(35)

把式(35)代入式(36)可得：

(36)

由式(29)和式(36)得到Vt的导数：

(37)

注意到条件(28)，则有：

(38)

这就是式(31)的推导过程。因此，函数Vt是有界的，很容易保证控制输入u是有界的。

定理1的结果表明，跟踪误差函数p2对z2具有相同的稳定性。这说明在同样的条件下，即相同的有限的ε值，滤波器时间常数和不确定性，z2和p2可能获得相同的解。但是，它们与跟踪误差z1的关系是不同的，可以用传递函数Gz(s)和GP(s)来说明解释。注意k1=ka，则存在：

Gp(s)=Gz(s)Gh(s);Gh(s)=s/(s+kb)

(39)

式中，Gz(s)为一个低通滤波器，而Gh(s)为一个高通滤波器，因此，Gp(s)可以同时减弱高频动态和低频动态。已知‖Gh(s)‖<1，会使得‖Gp(s)‖<‖Gz(s)‖。对于一个有限小的ε，不能确保z2和p2的渐近收敛，因此在不确定性存在的情况下，只能保证误差在某一范围内。因此，2DOF-IMC-SMC策略下的跟踪误差z1明显要小于SIMC-SMC策略。

3 仿真结果

3.1 阶跃扰动下的阶跃响应

首先进行仿真验证，给定伺服系统的标称模型为

(40)

令所需轨迹的滤波时间常数为λ=0.01。对以下4个控制器进行比较。

(1)SIMC-PD：表示基于内模控制的标准控制器，其相应的控制器参数很容易得到，即kp=0.1，kD=0.1。

(2)SIMC-SMC：这是基于标准内模控制策略和滑模控制方法所提出的鲁棒PD控制器(10)。PD控制器参数与SIMC-PD相同。参数变化范围为φ1min=[2500,1]T，φ2max=[2000,100]T。输入扰动的上限为Dmax=1 Nm。

(3)2DOF-IMC-PID：这是式(18)中提到的基于2DOF-IMC原理设计的PID控制器。PID控制器参数为ka=6.25，kb=50，kc=0.032。定点滤波器设计为F(s)=(0.01s+1)/(0.02s+1)。

(4)2DOF-IMC-SMC：这是一种基于2DOF-IMC和SMC的鲁棒PID控制器式(22)。为了能够公平进行比较，PID控制器和定值滤波器的参数与2DOF-IMC-PID相同，边界条件与SIMC-SMC相同。

首先，在阶跃扰动的条件下对四种控制器的阶跃响应进行仿真比较。参考轨迹为阶跃值R(t)=1 rad，阶跃扰动为0.2 Nm。目标模型是标称模型，即G(s)=Gn(s)。图3为4种控制器的仿真结果。易知所有的控制器都达到了预设的定点跟踪性能。然而，在存在阶跃扰动的情况下，虽然SIMC-SMC控制器能明显降低稳态误差，但是无论是SIMC-PD控制器还是SIMC-SMC控制器均不能实现零稳态跟踪误差。相反，2DOF-IMC-PID控制器和2DOF-IMC-SMC控制器的跟踪误差收敛至零。2DOF-IMC- PID控制器的峰值跟踪误差为0.1 rad，而2DOF-IMC-SMC控制器的峰值跟踪误差为0.04 rad。说明在2DOF-IMC-PID控制器中引入鲁棒滑模控制律，可以进一步减小跟踪误差。仿真结果表明，无论是SIMC-PD或者2DOF-IMC-PID，在其中引入鲁棒滑模控制律均能有效抑制干扰，进一步提高跟踪精度。理想情况下，跟踪误差可以通过改变参数ε的值而任意小。

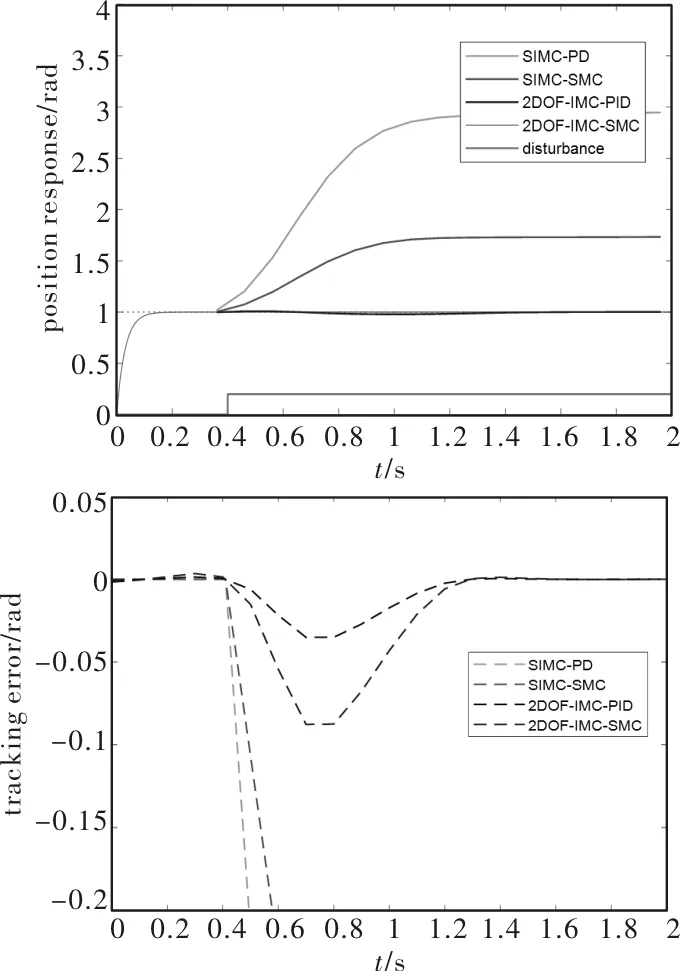
图3 在阶跃扰动下的位置阶跃响应

根据定理1可知，对于一个有限小的ε值，在恒定干扰的条件下，z2和p2中存在着稳态误差。由图4可知，当频率接近于零时，Gz(s)接近于一个常数，Gp(s)接近于零。这也是2DOF-IMC-SMC控制器可以实现零稳态误差，而SIMC-SMC控制器不能的原因。此外，在所有频率下，Gp(s)的大小都小于Gz(s)。因此，与SIMC-SMC控制器相比，2DOF-IMC-SMC控制器具有更好的瞬态跟踪性能和稳态跟踪精度。但是当频率足够大时，SIMC-SMC控制器和2DOF-IMC-SMC控制器的跟踪精度基本相同。

图4 波德图

3.2 参数不确定性时的阶跃响应

为验证该控制器的鲁棒性，测试了4种参数不确定条件下的仿真情况(J=2Jn,J=0.5Jn,B=10Bn和B=0.1Bn)。利用绝对跟踪误差最大值(Max|z1|)和绝对误差积分(IAE)这两个性能指标，对四种控制器的跟踪性能进行对比。

如图5到图8所示，分别为J=2Jn,J=0.5Jn,B=10Bn和B=0.1Bn的阶跃响应的对比仿真结果。表1总结了在4种控制器中，4种测试条件的性能指标(Max|z1|和IAE)，易知SIMC-SMC控制器和2DOF-IMC-PID控制器比SIMC-PD控制器具有更好的瞬态和稳态响应。将鲁棒滑模控制律引入到2DOF-IMC-PID控制器中，得到了2DOF-IMC-SMC控制器，跟踪性能(Max|z1|和IAE)得到进一步改善。通过滑模控制策略设计的鲁棒控制律，减小了参数变化对控制系统性能的影响，从而提高了跟踪精度。

图5 J=2Jn,B=2Bn时的阶跃响应

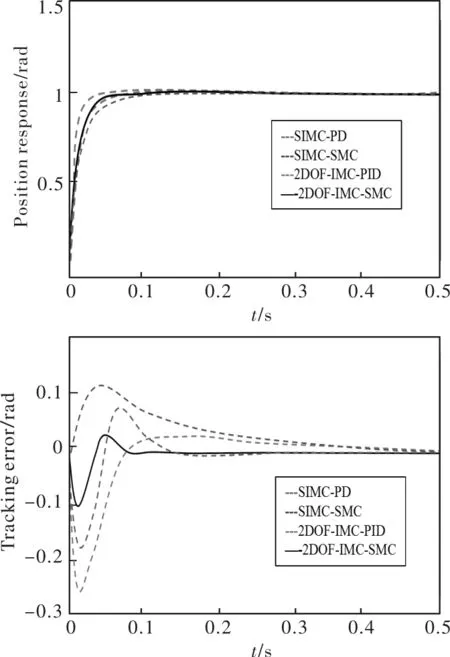
图6 J=0.5Jn,B=Bn时的阶跃响应

表1 跟踪响应的Max|z1|和IAE

同样，在不确定性的条件下，在具有有限小 的SIMC-SMC策略中会存在某一范围的跟踪误差。通过对SIMC-SMC和2DOF-IMC-SMC仿真结果的比较，不难看出，当一种鲁棒性较强的增强型IMC控制器应用于这种新型控制结构时，可以进一步提高控制系统的跟踪性能。

因此，不管是存在外部干扰还是存在参数不确定的情况，所提出的2DOF-IMC-SMC控制器相比于其他控制器均是最优的。

4 实验验证

4.1 实验设置

图9所示的实验平台由一个运动系统，包括交流伺服电机，20位增量编码器MSMJ042G01，交流伺服驱动MBDHT2510A1和惯性载荷的轴接头，电源，Beckhoff工控机C6930和包括CANopen和EtherCAT的控制测量系统所组成。系统软件包括监控软件(Twincat 3.0 Scope View)和实时控制软件(Twincat 3.0 eXtended Automation Engineering)。利用C/ C++代码的模块执行控制算法，采样间隔为0.25ms。利用C/ C++代码的模块编写不同控制器的控制代码，通过实时控制软件对扰动以及相应的不确定性进行模拟。实验原理为：工控机实现模型、控制器的设置以及相关参数的计算，CAN总线实现数据的传输，交流伺服电机则为相应的控制对象，通过测量伺服电机的状态变量，在工控机中形成偏差。经过相应控制器的计算给出控制量，实现伺服电机的控制。

图9 伺服系统的实验平台

在该伺服系统中，转动惯量为Jn=1.6×10-4kg·m2，粘滞摩擦系数为Bn=0.001 Nm/(rad/s)。伺服驱动器在转矩控制模式下运行。位置由20位旋转编码器测量。速度通过位置信号的后向差分获得。由于SIMC-PD控制器的抗干扰性能较差，因此只比较了3种控制器(SIMC-SMC、2DOF-IMC-PID和2DOF-IMC-SMC)。控制器参数和边界条件与仿真试验结果基本一致。

4.2 扰动条件下的位置跟踪

由于伺服系统不可避免地会受到参数偏差、非线性摩擦和被忽视的高频动态的影响，无法实现理想的定点跟踪和阶跃扰动响应。本实验采用广泛应用于各种定位控制系统的点对点参考运动轨迹，测试了三种控制器在不同输入干扰下的控制性能。最大速度为vmax=40 rad/s，最大加速度为amax=200 rad/s2。在u中加入两种输入扰动，测试伺服系统的抗干扰性能。一个是阶跃扰动，幅值0.2Nm。另一个是正弦扰动，为0.2(1-cos(12.56t))Nm。阶跃扰动下的实验结果如图10所示。三种控制器的性能指标(Maz|z1|和IAE)如表2所示。可以看出，在阶跃扰动存在的情况下，SIMC-SMC控制器存在稳态误差，这是由于滑模控制的边界层解和SIMC-PD的抑制扰动能力差造成的。2DOF-IMC-PID控制器是一种基于IMC方法的改进控制器，它在稳态跟踪误差方面比SIMC-SMC控制器要好，有着更好的跟踪性能。将基于滑模控制技术的鲁棒控制律加入到2DOF-IMC-PID中，跟踪系统的性能指标Max|z1|和IAE都会得到进一步的改善。实验结果如图10所示，与仿真结果如图4所示一致。在正弦扰动下的实验结果如图11所示。可以看出，在所有控制器中，2DOF-IMC-SMC再一次成为跟踪精度最高的控制器。实验结果如图10和图11所示，验证了所提出的控制器在加强抑制扰动能力方面的有效性。

图10 阶跃扰动下的位置跟踪误差

图11 正弦扰动下的位置跟踪误差

表2 阶跃扰动下跟踪Max|z1|和IAE

4.3 不确定条件下的位置跟踪

正弦状参考轨迹为R(t)=10(1-e-t)(1-cos(12.56t))rad，如图12所示，对3种控制器(SIMC-SMC、2DOF-IMC-PID和2DOF-IMC-SMC)的鲁棒性进行了测试。

图12 正弦型参考轨迹

(1)情况A：在此情况下，将0.5u应用于伺服系统，其中u可以通过各种控制策略进行计算。根据式(2)，此情况相当于把参数φ1改变为为0.5φ1，可以用来测试控制器的鲁棒性。

(2)情况B：这种条件是将u-0.01x2作为控制输入。同样地，这种情况下参数φ2会发生很大的变化，φ2变为0.01φ1+φ2，可以用来测试控制器的鲁棒性。

已知φ1=1/J以及φ2=B/J，其中1.6×10-4kg·m2，B=0.001 Nm/(rad/s)，所以得到了上述两种类型的不确定性的边界大小。

图13和图14分别为A和B两种情况下的实验结果，3种控制器的性能指标(Max|z1|和IAE)如表3所示。很容易看出，在存在不确定φ1和φ2的情况下，2DOF-IMC-SMC控制器比SIMC-SMC控制器和2DOF-IMC-PID控制器具有更好的跟踪精度。验证了该控制策略对提高控制系统鲁棒性的有效性。由于基于滑模控制技术的鲁棒控制律能够减弱不确定性的影响，因此2DOF-IMC-SMC比2DOF-IMC-PID具有更好的跟踪精度。此外，与SIMC-PD控制器相比，2DOF-IMC-PID控制器可以更好地提高闭环系统的鲁棒性，从而可以更好地减少由于滑模控制方法边界层解而产生的跟踪误差。由于结合了加强内模控制与鲁棒滑模控制，在3种控制器中，2DOF-IMC-SMC控制器鲁棒性最佳。

图13 情况A下的位置跟踪误差

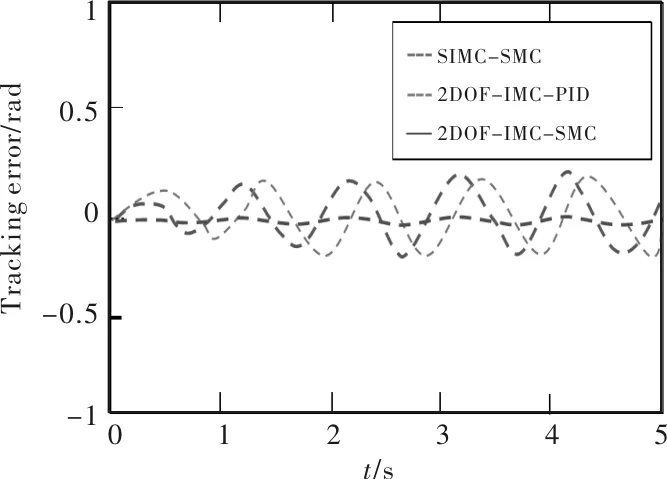
图14 情况B下的位置跟踪误差

表3 正弦跟踪下的Max|z1|和IAE

5 结 论

文章针对伺服电机在不确定性和扰动情况下的运动控制，设计了一种基于鲁棒滑模策略的双自由度增强型内模控制器。通过仿真与实验结果得到如下结论：

(1)鲁棒滑模控制律的引入能有效抑制干扰和不确定性，提高控制器的跟踪精度。

(2)在频率较小条件下，双自由度增强型内模控制相比于传统内模控制能更好地降低参数变化的敏感性，减小未知扰动的影响，具有更好的瞬态跟踪性能和更高的稳态跟踪精度。

(3)结合鲁棒滑模策略的双自由度增强型内模控制能够保证跟踪渐进稳定，且无论对于外界扰动或者不确定性均展示了较好的鲁棒性，跟踪精度较高。