反演导热系数的计算方法在热处理工艺的应用
张继涛,赵丽民,巩笑源
(1.精功(绍兴)复合材料有限公司,浙江 绍兴 312000;2.精功(绍兴)技术研发有限公司,浙江 绍兴 312000)
1 引言
目前国内外致力于齿轮材料研究和热处理工艺的优化,而热处理模拟技术点的关键在于理论模型的建立、实验数据的准确提取、模拟设备和验证技术的完善。早期,Davenpore 和Bain 在文章中研究TTT 曲线,也就是等温转变情况,组织转变量和温度、时间之间的关系,利用TTT 曲线预测组织转变情况。但是实际生产当中,得到连续冷却条件下的实际组织转变和理论模型计算差别太大,TTT 曲线无法与实际生产相联系[1]。70 年代初,Inoue 开始提出组织转变数值模拟的概念[2],利用Grange 和Kiefer 提出组织转变曲线(CCT 曲线),将其作为组织转变模拟的依据,CCT 曲线是描述不等温冷却过程的曲线,反映了各种组织转变起始点对应的温度以及转变过程组织转变量[3]。80 年代之后,理论上逐步完善相变模型,针对温度场的非线性求解,人们引入有限元技术,这使得淬火模拟技术发展更进一步[4-6]。
反向热传导问题广泛的应用于研究。由于实际工程问题的复杂性,求解热传导反问题所涉及的计算量也非常大,因而比求解正问题困难得多,如何求解该类问题吸引了众多研究者的关注。反向热传导的特点:首先由于边界热流和换热状况是待预测的,故其数学定解问题是不适定的,因而严格来说是无定解的,或者是很难求解的[7]。然而在Deform-3d 软件中却很容易完成,在Deform-3d 中的最优化算法是采用的共轭梯度法,而共轭梯度法在反向热传导最优化算法的精确性是被前人所验证的。所以基于Deform-3d 分析的反向热传导问题程序简单节省时间并且结果可靠[8]。本文针对齿轮制变形大、表面完整性低、精度稳定性低等问题,开展18CrNiMo7-6 齿轮材料残余应力和热处理变形演变机理研究,首先利用Deform 反传热模型首先假定表面换热系数初值,通过导热微分方程推算内部温度值,然后根据推算值与实验测定值的差值不断修正设定值,最终使推算值逼近测定值,求得表面换热系数,用于热处理数值计算中作为边界条件,之后根据混合相的计算规则,基于优化的硬度模拟模型,对渗碳淬火过程的硬度预测进行了研究,突破齿轮热处理变形控制等关键技术,分析齿轮在不同热处理工艺条件下组织与几何尺寸变化规律。
2 热处理理论基础
渗碳-淬火过程的模拟可以看作是金属-热-机械耦合计算,整个模型包括四个部分:1)组织转变分析,其中包含用于硬度预测的所有硬度计算方程式;2)渗碳过程分析,用于分析渗碳过程中碳的扩散;3)温度场分析,主要用于分析整个过程中的热传导;4)相变动力学分析,研究渗碳淬火过程中的金相组织转变规律。
2.1 热传导模型
在热传导过程中,假设材料各向同性,由于齿轮每个位置与空气、冷却液的对流换热作用不一样,导致齿轮温度场的差异,采用传导方程由公式(1)求解,其考虑材料相变释放的潜热[9]。

式中:ρ—材料密度;kt—热传导系数;Cp—热容:ΔH—潜热。
在加热和渗碳过程中,齿轮表面热传递满足边界条件[10],由公式(2)所示:

式中:h—对流换热系数;Te—齿轮加热和渗碳过程的轮齿温度;Ts—环境温度。
2.2 相变模型
在进行热处理前,斜齿轮的组织初相为铁素体和珠光体,经过奥氏体化阶段,铁素体和珠光体开始转变为奥氏体[11],这一过程是扩散相变过程,在此阶段齿轮表面的碳含量均一化,相变动力参数呈现为与温度相关,简化扩散公式为:

式中:βA—奥氏体体积分数;A、D—材料常数(分别取-4 和2);Ae1、Ae3—分别是根据CCT 图得到的组织转变的上、下临界温度;T—齿轮渗碳过程中的轮齿温度。
奥氏体化后,奥氏体经过冷却转变为铁素体、珠光体、贝氏体、马氏体,运用Jmatpro 软件,计算组织转变温度点如表1 所示。

表1 组织开始转变临界温度点
在淬火之前模拟渗碳工艺,导致齿轮各部位碳浓度的非均质分布,在冷却和淬火过程中,奥氏体转变为子相,对应组织转变是等温相变,非扩散型相变服从麦基方程[13],即式(4):

式中:X—马氏体转变体积分数;Ms—马氏体相变温度;T—绝对温度。
2.3 应力应变模型
热-弹-塑性分析是热处理仿真的计算的主要组成部分,热处理残余应力是工件经过热处理后最终残存下来的应力,对工件的形状尺寸和性能都有极为重要的影响,工件在加热和冷却的过程中,由于温度差在热胀冷缩的作用下产生热应力,工件变形和位移是热应力作用的结果,其计算由公式(5)所示:
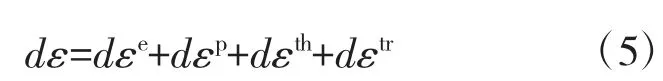
式中:dεth—热应变增量;dεe—弹性应变增量;dεp—塑性应变增量;dεtr—相变应变增量;dε—应变增量。
从材料的塑形性能考虑,其流动应力表达式为:

式中:T—齿轮温度;Y—屈服强度;C—碳含量;H—硬化模量;—等效应变。
3 表面换热系数的计算
图为表面换热系数的计算流程。Deform 反传热模型首先假定表面换热系数初值,通过导热微分方程推算内部温度值,然后根据推算值与实验测定值的差值不断修正设定值,最终使推算值逼近测定值,对于计算所得表面换热系数的精度,可通过应用其所获得的温度预测值与实测值的对比判定。
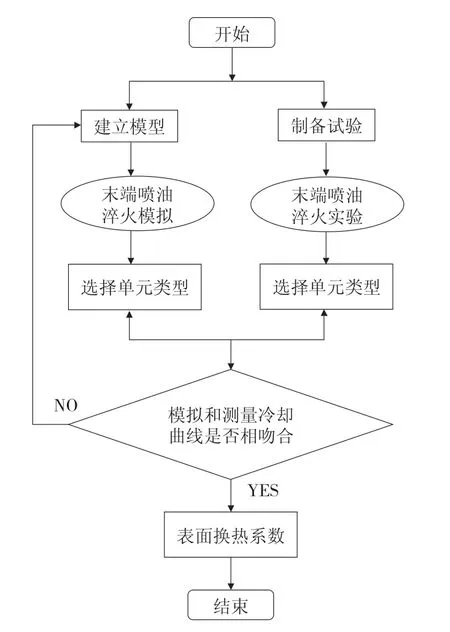
图1 表面换热系数的计算流程
3.1 试验方案及冷却曲线
试验设备采用自制末端喷油淬火试验机。选用端淬试样为带台阶的圆柱体,在试样的凸台部位中心向里面用电火花打孔,中部和底部放置热电偶。试样尺寸和放热电偶位置如图2 所示。采用长2 m,直径1 m 的镍铬-镍硅热电偶,经标准热电偶校验,在0 ℃~1 000 ℃间该热电偶的测量误差为±2 ℃,动态响应时间为0.05 s,符合试验精度要求。

图2 喷油末端淬火试样图示
采用Deform 软件的反传热模型求解表面换热系数,并通过改变控制参数,分析其对温度预测精度的影响。图3 为反传热的冷却曲线图。在反传热问题中,将表面对流换热系数作为优化变量,测点温度计算值与测量值之间的残差作为优化目标函数,通过极小化目标函数进行仿真,模型计算所用的实测温度数据取自文献[11]。
3.2 反传热模型的建立及求解
本文拟求解表面换热系数关于温度的函数,采用Linear 线性插值。对于非线性数值问题,Deform反传热模型采用BFGS 优化算法控制,提高换热系数的计算效率。采用Deform-3D 有限元分析软件Inverse Heat Transfer 反传热模型,18CrNiMo7-6 圆柱体几何模型通过x_t 格式导入Deform-3D,材料属性通JMatPro、热处理手册及相关文献确定。已知18CrNiMo7-6 圆柱体的淬火温度860 ℃,淬火介质温度20 ℃.将实验测得的圆柱体中心测温点的温度数据导入反传热模型。由于淬火过程中温度变化剧烈,为提高计算效率,模型求解采用变时间步长0.001 s~10 s,每个时间步长的最大温度变化为1 ℃.

图3 反传热的冷却曲线图
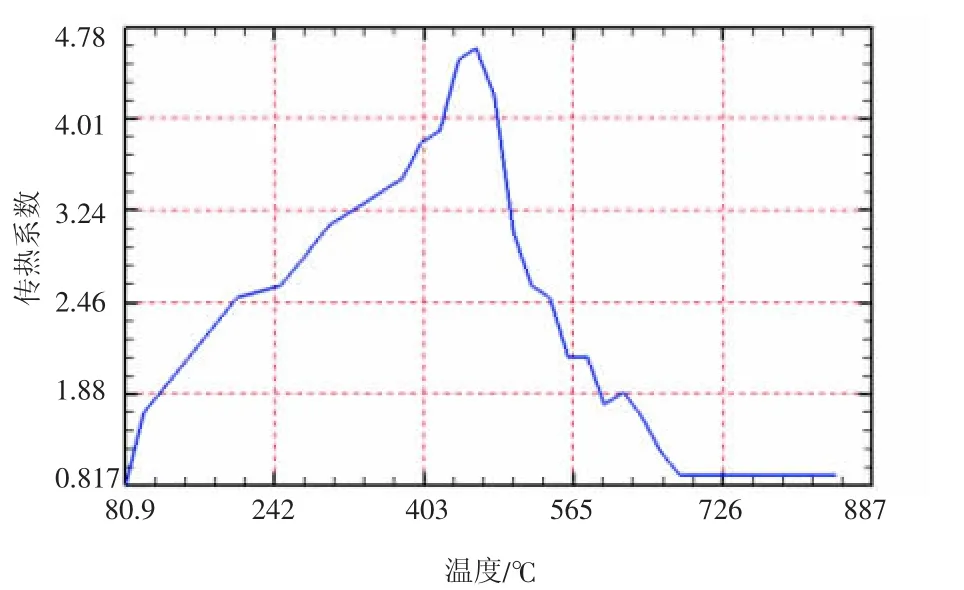
图4 表面换热系数
4 齿轮渗碳淬火过程的数值模拟
4.1 渗碳淬火模型的建立
表面改性技术与工艺作为改善齿轮表面完整性的关键措施,是提高材料和齿轮使用性能的核心和关键,渗碳淬火是常用的表面改性技术,可以提高齿轮表面硬度,具有良好的综合力学性能,可满足齿轮的较多技术要求,而表面淬火可以提高疲劳强度和耐磨性并保持芯部韧性。图5 为料齿轮热处理工艺流程图。齿轮热处理选择优质的生产工艺材料,可以保证齿轮获得优良热处理质量、防止产生热处理缺陷。

图5 斜齿轮热处理工艺流程图
4.2 材料属性和相关参数
对钢铁材料齿轮进行适当热处理,其目的是为了能够提高钢铁的使用寿命、充分发挥材料的优良性能,同时也能够提高齿轮表面质量,改善钢材的加工性能。18CrNiMo7-6 作为一种广泛使用的结构钢,本文将其作为齿轮材料,分析齿轮在渗碳淬火工艺组织性能与几何尺寸变化规律,其化学成分见表2.

表2 18CrNiMo7-6 低碳合金钢的化学成分(质量分数,%)
热物性参数有:热导率、密度和定压比热。一般来说这些参数并不是常数,是随材料的组织状态和温度而变化的,因此也是随时间的变化而变化。在计算浓度分布时需要材料的扩散系数。定压比热容和热导率随温度变化曲线分别如图6、图7 所示。

图6 比热容随温度变化曲线
4.3 边界条件的设定
根据试样的端部淬火,本文选用反演的表面换热系数作为温度场模拟的边界条件。
5 齿轮热处理数值模拟结果分析
DEFORM 是在一个集成环境内综合建模、成形、热传导和成形特性进行模拟仿真分析。本文使用热处理仿真软件DEFORM 模拟斜齿轮渗碳淬火工艺,计算流程如图8 所示。
5.1 表面力分析
表面扩张力、表面区域是表面力分析的主要环节,见图9.分析图9 a),表面扩张力指表面的承载能力,针对齿轮容易形成裂纹,由于热胀冷缩的原因,致使齿轮在不同工艺过程的向外扩张的能力是不同的,轮齿最薄处表面扩张力最大。分析图9b),表面区域是指单齿在加热和冷却的过程中,其表面受力不相同的区域。

图8 渗碳淬火计算流程

图9 表面力分析

图10 碳元素分布云图
5.2 碳元素分布
渗碳齿轮可以得到高的表面硬度和韧性的芯部,具有良好的综合力学性能,烧透还原、强渗过程和降温扩散是齿轮渗碳的三个过程[12]。图10 为渗碳处理后碳元素分布图。
由图10 可知,渗碳过程的每个阶段结束后的碳含量分布是不一样的,经过烧透还原、强渗碳和降温扩散后,渗碳后碳元素含量满足齿顶>齿面>齿根的规律,齿轮均匀渗碳,为之后的工艺制定提供良好的基础。

图11 碳淬火流程中碳元素的含量
图11 反映了整个渗碳淬火工艺过程中碳含量分布,随时间变化碳元素分布因位置不同而不同,图11b)表示不同深度的碳含量,齿顶的碳含量是最高的,高于其他部位,齿面与齿轮底面碳元素分布一样,齿根由于特殊的几何形状,碳原素扩散速率较低,导致齿根的碳含量最低。

图12 齿轮渗碳淬火温度云图

图13 齿轮渗碳淬火温度分布
5.3 温度场分布
图12a)、b)分别为淬火10 s 和100 s 时斜齿轮温度场。分析可知,齿面由于冷却速率快而温度下降快,齿轮底面与齿面温度下降速率相当。
图13 为斜齿轮不同部位温度随时间变化曲线图,由于齿面、齿顶的冷却速率快,所以齿顶温度下降速度最快;而冷却介质无法直接到达齿轮芯部齿轮,齿根和轮齿芯部由于冷却速率的特性,齿轮的温度下降趋势变缓慢。
5.4 组织场分布
在淬火之前模拟渗碳工艺,导致齿轮各部位碳浓度的非均质分布,在冷却和淬火过程中,奥氏体转变为子相,对应组织转变是等温相变。由表2 可知,马氏体的形成主要由轮齿含碳量和冷却速率影响,而马氏体的含量决定齿轮硬度,分析渗碳淬火后轮齿的性能,见图14.
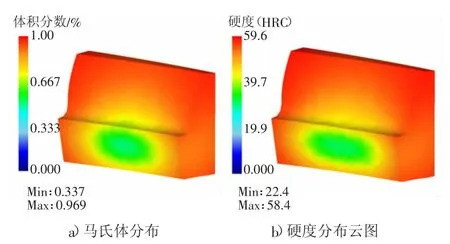
图14 斜齿轮组织分布
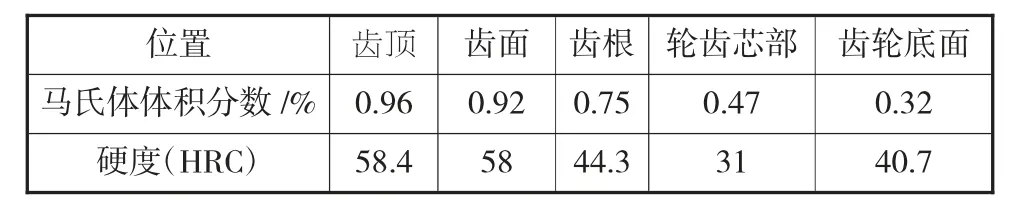
表3 齿轮整体的马氏体与硬度数值
由图14 可知,由于冷却速率的特性,齿轮表面冷却速率快,马氏体在齿轮转变积累多,因而含量相对较高;而芯部通过热传导散热冷却速率低,淬火形成的马氏体少,最终形成齿轮表面硬度高而芯部保持人性。渗碳淬火结束时,齿轮整体的马氏体与硬度数值布如表3 所示。
5.5 应力与应变
热处理残余应力是工件经过热处理后最终残存下来的应力,对工件的形状尺寸和性能都有极为重要的影响,工件在加热和冷却的过程中,由于温度差在热胀冷缩的作用下产生热应力,工件变形和位移是热应力作用的结果,图15 为斜齿轮切应力曲线图。

图15 斜齿轮切应力曲线图
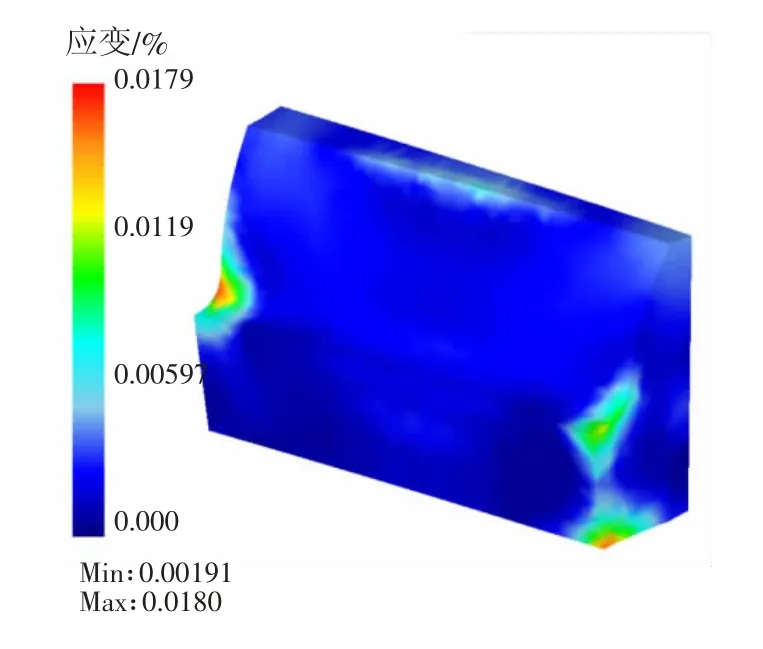
图16 斜齿轮热畸变图
在淬火前期时,轮齿表面呈现拉应力状态,芯部呈现压应力状态。这是因为表面降温速率远高于芯部,齿轮表层冷却较快,齿面因收缩产生拉应力,芯部温度较高,阻碍表层组织收缩,而呈现压应力状态。在此之后温度的快速下降,在100 s 左右达到稳态,齿顶、齿面呈现压应力,大小分别为380 MPa、240 MPa,轮齿芯部呈现拉应力为180 MPa.
图16 为斜齿轮热畸变图。由图16 可知,在轮齿根部和中部齿顶处明显存在较大的热畸变。齿顶产生鼓形变形,这是因为齿轮中部相对散热慢,在热应力的作用下呈现中部凸起。
6 结论
本文基于反向热传导问题,利用Deform 反传热模型首先假定表面换热系数初值,通过导热微分方程推算内部温度值,然后根据推算值与实验测定值的差值不断修正设定值,最终使推算值逼近测定值,求得表面换热系数,在热处理数值计算中作为边界条件,使用专业模拟软件Jmatpro 预测低碳钢18CrNiMo7-6 的材料性能,然后导入Deform 软件对斜齿轮渗碳淬火热处理,仿真结束得到齿轮碳元素分布云图、温度场、组织场、应力场和齿面对应位置硬度,得到以下结论:
1)渗碳后碳元素含量满足齿顶、齿面、齿根依次下降的规律,渗碳后进行淬火工艺,由于碳含量的分布情况,表面硬度和残余应力也符合相应的规律。
2)齿轮渗碳淬火后得到表面碳含量高、芯部含量低,达到了表面硬化、芯部保持韧性,从而达到提高疲劳强度和耐磨性,并且保持芯部韧性的优良综合性能。
3)由于金相组织变化和热应力的综合叠加结果,在淬火前期时,轮齿表面呈现拉应力状态,芯部呈现压应力状态。在此之后温度快速下降,在100 s左右达到稳态,齿顶、齿面呈现为380 MPa、240 MPa压应力,轮齿芯部呈现拉应力为180 MPa.
结果表明,Deform 软件可以反演具有函数形式的导热系数,由此证明,本文提出的基于Deform 反演系数随温度变化的导热系数的预测模型具有较高的精度,并且方法简单,易于实现,可广泛应用于各类材料的导热系数的预测,对材料研究以及用于加工零件的材料性能的后续研究具有良好的借鉴意义。由于物理实验条件匮乏,本文只进行了仿真虚拟实验,实际上,为了更准确的预测材料的导热系数,理论模型和仿真模型都应更贴合实际,有条件还应进行物理实验验证。其次,文中忽略了环境温度的变化对测点温度的测量值的影响,这些都有待今后的进一步研究。

