火卫一周期准卫星轨道及入轨分析
吴晓杰,王悦,
(北京航空航天大学 宇航学院,北京102206)
中国的火星探测计划已于2016年立项实施,与火星相关的轨道设计工作相继展开[1],其中火卫一和火卫二的探测工作是计划中的重要部分。火星有2颗天然卫星:火卫一Phobos和火卫二Deimos。随着人类空间探索研究的不断进展,火卫一在空间探索中的作用越来越重要:在行星科学方面,火卫一是人类研究太阳系及其行星系统起源的重要样本;在航天工程方面,火卫一因其较小的逃逸速度,成为了人类空间探索中转站的理想天体[2]。
在火卫一的探测任务设计中,设计稳定的环绕轨道,尤其是周期环绕轨道,是关键步骤。然而,由于火卫一的质量和轨道半长轴都很小,在火星强大的第三体引力摄动下,它的Hill球半径只比星体表面高出几公里。在这种情况下,利用经典的受摄Kepler轨道实现火卫一环绕任务几乎是不可能的。因此,在解决其环绕轨道的问题时,必须考虑引入多体问题进行求解。基于前人的研究成果,准卫星轨道(Quasi-Satellite Orbits,QSOs)已经被证明可以在一定的条件下稳定存在于火卫一的邻近区域内[2]。日本宇宙航空研究开发机构(JAXA)、欧洲航天局(ESA)和法国国家太空研究中心(CNES),都在计划中的MMX(Mars Moon eXplorer)任务中规划了对火卫一的准卫星轨道环绕任务[3-4]。
对于三体问题模型下火卫一准卫星轨道的研究工作,最早由W iesel及其研究团队进行的[5-6]。W iesel[6]将限制性三体问题模型应用于火星-火卫一-飞行器系统,探究了影响火卫一准卫星轨道稳定性的各种因素。其学生Jansson[5]首次使用庞加莱截面的方法,以圆型限制性三体问题(CRTBP)为模型分析了火卫一和火卫二邻近区域准卫星轨道的稳定性。Tuchin[7]在研究火卫一准卫星轨道时使用考虑火卫一偏心率的Hill模型,并在该模型下提供了一种轨道设计方法,以满足给定的覆盖、时间和距离约束。Gil和Schwartz[2]做了大量关于准卫星轨道数值分析方面的尝试,对火星火卫一系统进行了相空间数值搜索,证明了稳定准卫星轨道的存在性,并分析得到了三维稳定准卫星轨道的一系列特性。Cabral[8]从解析与数值的角度对椭圆型限制性三体问题(ERTBP)模型下的火卫一准卫星轨道稳定性进行了探究,给出了准卫星轨道在特定时间范围内的数值稳定解。Wallace等[9]采用考虑摄动的圆型限制性三体问题模型对火星系统的多种类型轨道进行了研究,其中包括准卫星轨道和平动点轨道,并设计了这两种轨道之间的转移策略,以适应火卫一探测任务的需要。Zamaro和Biggs[10-13]通过引入球谐引力势的方法进一步提高了模型的精度,并进行了一系列研究工作,揭示火卫一附近的准卫星轨道和平动点轨道等非Kepler轨道的特性,以及它们之间的低能转移轨道。随着相关研究的开展,更高精度的模型被应用到火卫一的轨道设计中。基于火星探测飞行器在与火卫一的近距离飞掠中得到的影像数据,火卫一多面体几何模型与引力场受到许多学者的关注与研究[14-18]。Scheeres等[19-20]建立了基于多面体模型的限制性三体问题动力学方程,并使用了多面体模型系统分析了火卫一邻近区域的平动点轨道和准卫星轨道,这是到当时为止描述火星火卫一系统最精确的模型。
本文的研究主要集中于火卫一附近的周期准卫星轨道以及从环火星轨道到准卫星轨道的转移轨道。准卫星轨道一般距离次级天体较远,是一种高度远高于拉格朗日点L1和L2的逆行轨道。因此,本文将火卫一看作质点,忽略其非球形引力场,并假设火卫一围绕火星做圆运动,即采用圆型限制性三体问题模型。
基于这些假设,本文首先使用Jansson的方法[5],利用庞加莱截面与KAM 理论研究火卫一邻近区域的准卫星轨道的稳定性,给出不同能量条件下准卫星轨道的稳定区域,将它绘制在相应的庞加莱映射中。然后,提出一种KAM 环迭代方法,利用庞加莱截面法得到的稳定区域进行迭代,从而得到稳定区域内的周期准卫星轨道解。最后,提出一种准卫星轨道的入轨设计方法:假设周期轨道经过一个速度脉冲实现入轨,反推出飞行器由转移轨道到达入轨点的速度,再做反向积分,直到离开火卫一邻近区域,从而生成一条从火星环绕轨道转移到火卫一周期准卫星轨道的转移轨道。
1 动力学
1.1 坐标系
圆型限制性三体问题的运动方程是建立在质心旋转坐标系中的:原点位于火星(如图1中m1所示)与火卫一(如图1中m2所示)的质心处,坐标系x轴由火星指向火卫一,z轴与火卫一轨道角动量方向一致,如图1所示。由于火星与火卫一固定于x轴,因此整个坐标系以火卫一公转角速度为角速度绕z轴旋转。图1中坐标系XOY代表原点在火星与火卫一质心的惯性坐标系,系统中的某质点P在2个坐标系之间的转换关系与两坐标系间的夹角t相关。
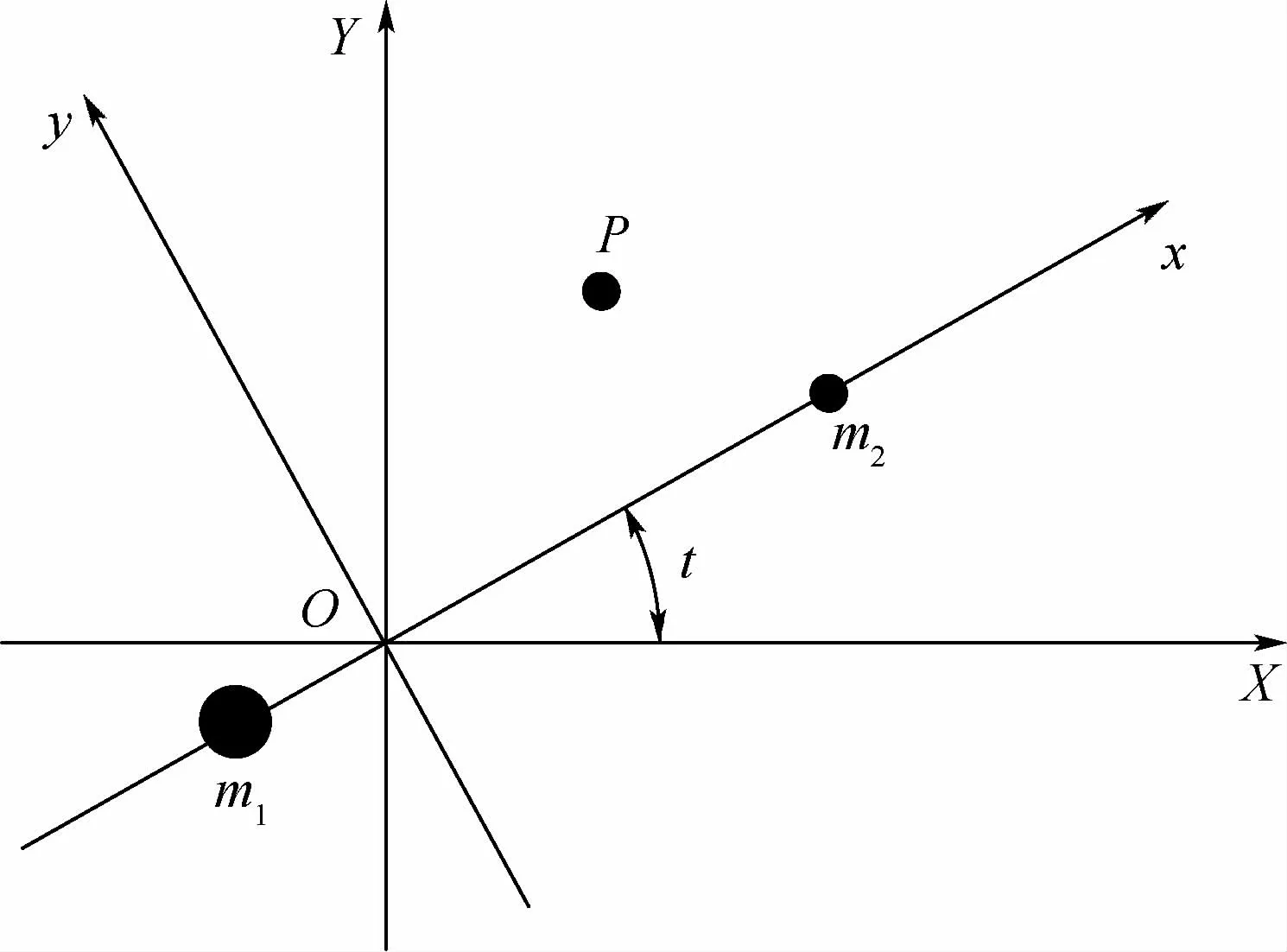
图1 原点位于火星火卫一系统质心的旋转坐标系Fig.1 Synodic coordinate system with origin at the barycenter of Mars and Phobos
1.2 圆型限制性三体问题
可以将火星、火卫一与飞行器看作一个三体系统,考虑到火星与火卫一的质量远大于飞行器质量,描述该三体系统的动力学模型是一个限制性三体问题模型。火卫一围绕火星的轨道是一个小偏心率椭圆,本文近似假设火卫一的轨道为圆轨道。这时,整个系统模型简化为一个圆型限制性三体问题。Cabral给出了圆型限制性三体问题的动力学方程为[8]


本文主要研究飞行器在火卫一轨道平面内的运动。因此,考虑平面情况下的圆型限制性三体问题,即运动参数中的z≡0,˙z≡0。在计算中,飞行器与火卫一的距离比其相对于系统质心的距离更有实际意义。因此,本文参考Cabral[8]的坐标变换方法,将系统坐标系做平移变换,使得火卫一成为坐标系的原点。系统的运动方程变为

1.3 Jacobi积分
由式(4)、式(5)可以看出,运动方程是时间无关的,存在首次积分,反映飞行器的能量,常选为Jacobi积分,即

式中:E为飞行器的总机械能。
1.4 庞加莱截面与KAM 环
庞加莱截面是分析多变量自治系统的一种有效方法。假设相空间中存在一个超平面(即飞行器运动变量的一个等量关系),飞行器的运动若与该平面相交,则会在相平面上留下一个轨迹点。庞加莱截面上的轨迹点可以反映飞行器运动的稳定特性:如果截面上是一个或是几个离散的点,运动是周期的;如果截面上是杂乱无章的散点,则运动是混沌的;如果截面上形成一些连续的环,则运动是拟周期的,这些连续的环被称为KAM环。
本文的庞加莱截面选取如下:经过火星与火卫一,垂直于火卫一轨道平面,并处于火卫一轨道外侧的半平面,如图2所示。

图2 庞加莱截面Fig.2 Poincaré’s surface of section
2 周期准卫星轨道及入轨分析
2.1 准卫星轨道庞加莱映射
在平面圆型限制性三体问题中,飞行器的运动状态由2个位置参数和2个速度参数决定,具有一个四维的相空间。当给定Jacobi常数时,飞行器的4个状态参量须满足给定的能量指标,因此系统维数降低为三维。如果考查1.4节中给出的庞加莱截面上轨迹点情况,则系统运动状态可以由2个状态参数确定。系统的庞加莱映射会随着系统Jacobi常数的变化而发生变化,因此可以根据Jacobi常数来区分不同能级的准卫星轨道,特别是周期准卫星轨道。不同Jacobi常数下的准卫星轨道庞加莱映射如图3所示。
从图3中可以看出,庞加莱映射可以反映特定的Jacobi常数下准卫星轨道的敛散性。当轨道初始条件选取合适时,准卫星轨道表现出良好的稳定性,做拟周期运动,并在庞加莱映射中表现为环形,即KAM 环。这些KAM 环围成的区域,称为稳定岛。而在KAM 环状区域以外,轨道是混沌的,运动状态处在这一区域的飞行器很难保证可以长期稳定于火卫一的邻近区域。
将不同的Jacobi常数对应的庞加莱映射中稳定岛的边界绘制在同一张图上,可以得到稳定岛大小与分布随Jacobi常数的变化情况,如图4所示。由图4可以看出,随着Jacobi常数增大,稳定岛的位置逐渐靠近原点,其面积也逐渐减小,故较小的Jacobi常数意味着存在更大范围的稳定轨道。因此在进行火卫一准卫星轨道设计时,需要根据任务约束选择合适的Jacobi常数。
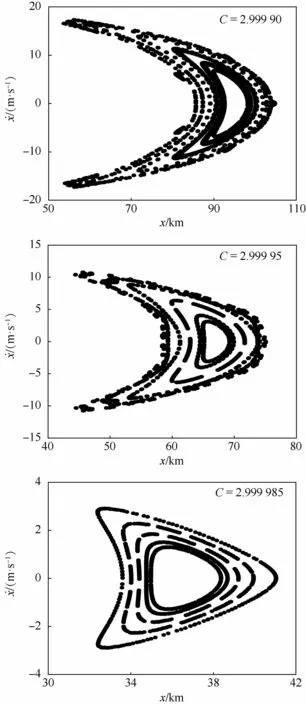
图3 不同Jacobi常数下的庞加莱映射Fig.3 Poincaré’s maps with different Jacobi constants
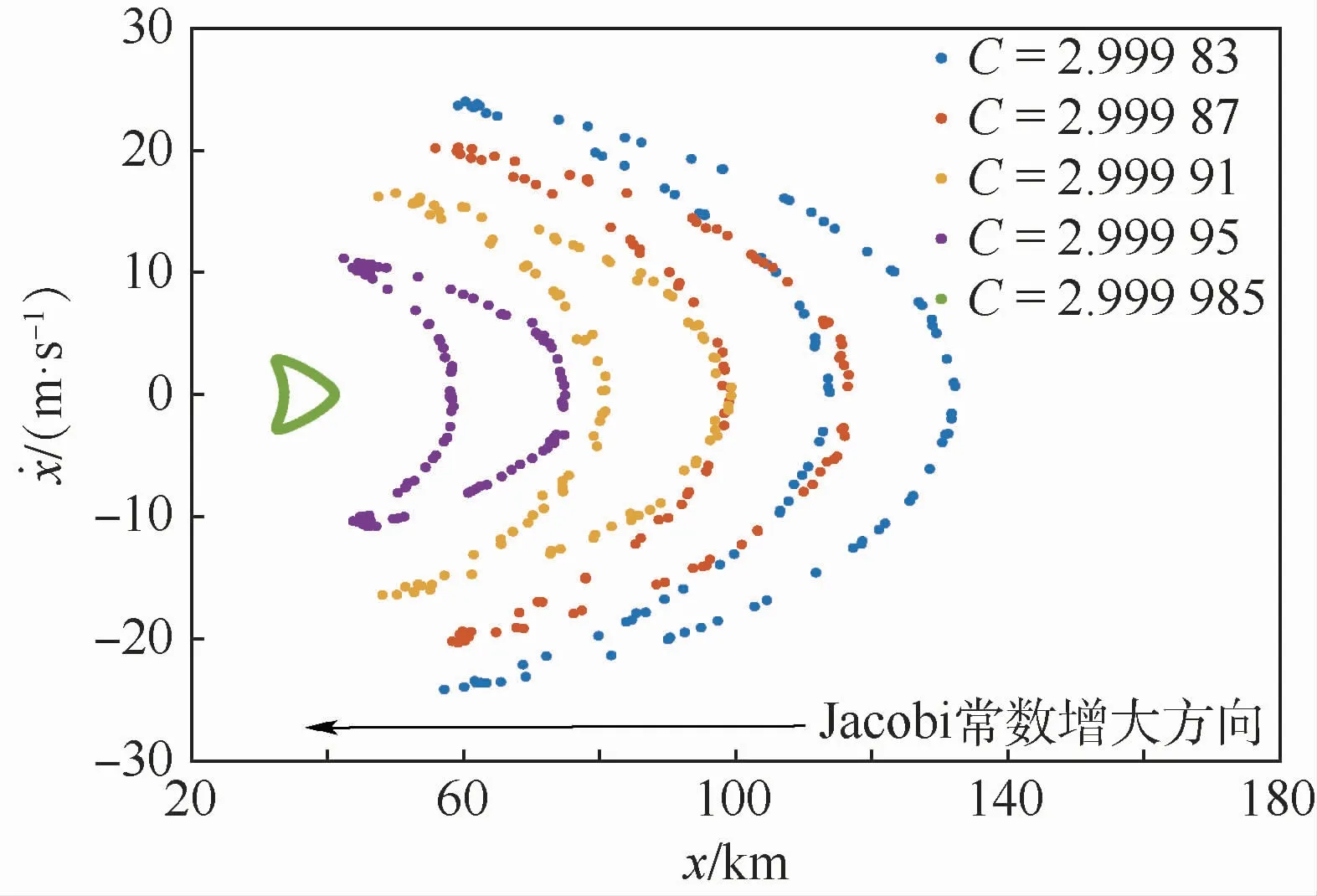
图4 不同Jacobi常数下的庞加莱映射边界Fig.4 Poincaré’s maps’borders with different Jacobi constants
2.2 周期准卫星轨道
给定飞行器合适的初始运动状态,其相空间轨迹将在庞加莱截面上形成一个环面,即KAM环,且不同初始条件下的KAM 环是互不相交的。如果在这个环的内部确定一个点,作为下一条准卫星轨道的初始条件,则新的KAM 环就处于原KAM环的内部,而且该环所围成的面积小于原KAM环。重复这个过程,轨道在截面上形成的KAM环尺寸会越来越小,直到小于对轨道周期性的精度要求,从而得到一条符合Jacobi常数条件的周期准卫星轨道。这种迭代求解周期准卫星轨道的方法就是KAM 环迭代法。迭代过程如图5所示。
应用这一方法,可以得到环绕火卫一的周期准卫星轨道族,如图6所示,其初始条件如表1所示。
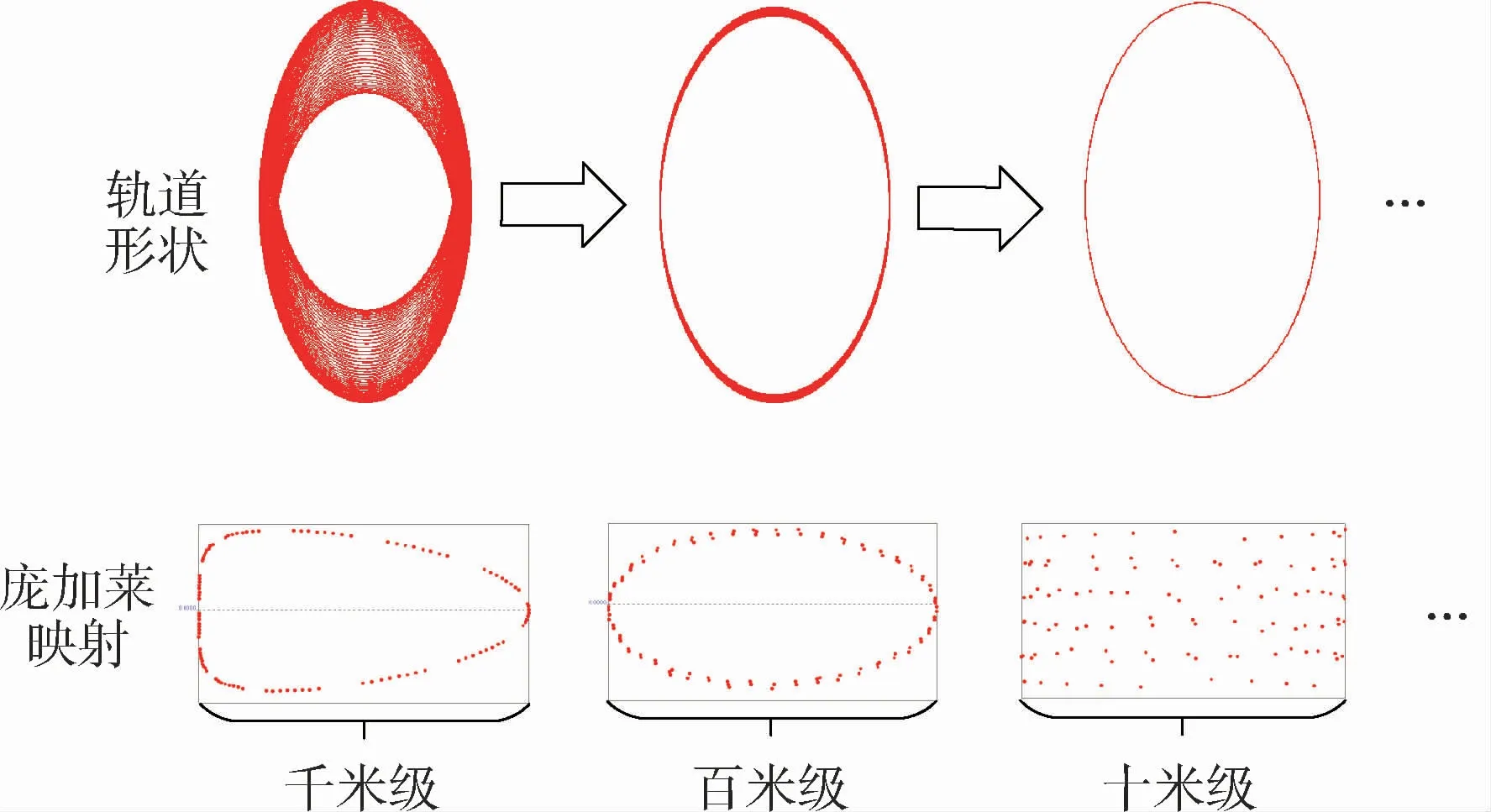
图5 一个典型的KAM环迭代过程Fig.5 A typical KAM tori iteration process

图6 周期准卫星轨道族Fig.6 Periodic QSO family
2.3 周期准卫星轨道入轨分析
在实际的火卫一探测任务中,飞行器往往是首先被火星捕获,进入火星的环绕轨道,再由火星环绕轨道进行转移,最终进入准卫星轨道。因此,需要设计从火星环绕轨道到火卫一准卫星轨道的转移轨道。
本文设计的轨道转移方法,是将周期准卫星轨道与庞加莱截面的交点作为入轨点,当飞行器在火星与火卫一的共同作用下到达入轨点时,施加一个速度脉冲进入准卫星轨道。由表1可知,在确定的Jacobi常数下,周期准卫星轨道具有一个确定的初始速度Vp。假设飞行器在转移轨道上也垂直穿越庞加莱截面,并在其速度方向上施加一个速度脉冲ΔV,以实现周期准卫星轨道入轨,其到达截面时的速度就可以通过周期准卫星轨道的截面速度与速度脉冲之差得到,进而反向积分就可得到飞行器到达入轨点之前的运行轨迹,该轨迹在本文中被称为回溯轨道。ΔV的正负由本文定义坐标系确定,即,当ΔV为正时,速度脉冲方向沿y轴正向。周期准卫星轨道在本文给定庞加莱截面上速度均为负值,因此,当ΔV为正时,施加在飞行器上的是减速脉冲。飞行器变轨至该轨道,经过一段时间的飞行就会进入火卫一的引力影响球,并在火星与火卫一的共同作用下抵达庞加莱截面。此时对飞行器施加前述的速度脉冲ΔV,就可以进入周期准卫星轨道。图7给出了C=2.999 890时的转移过程。
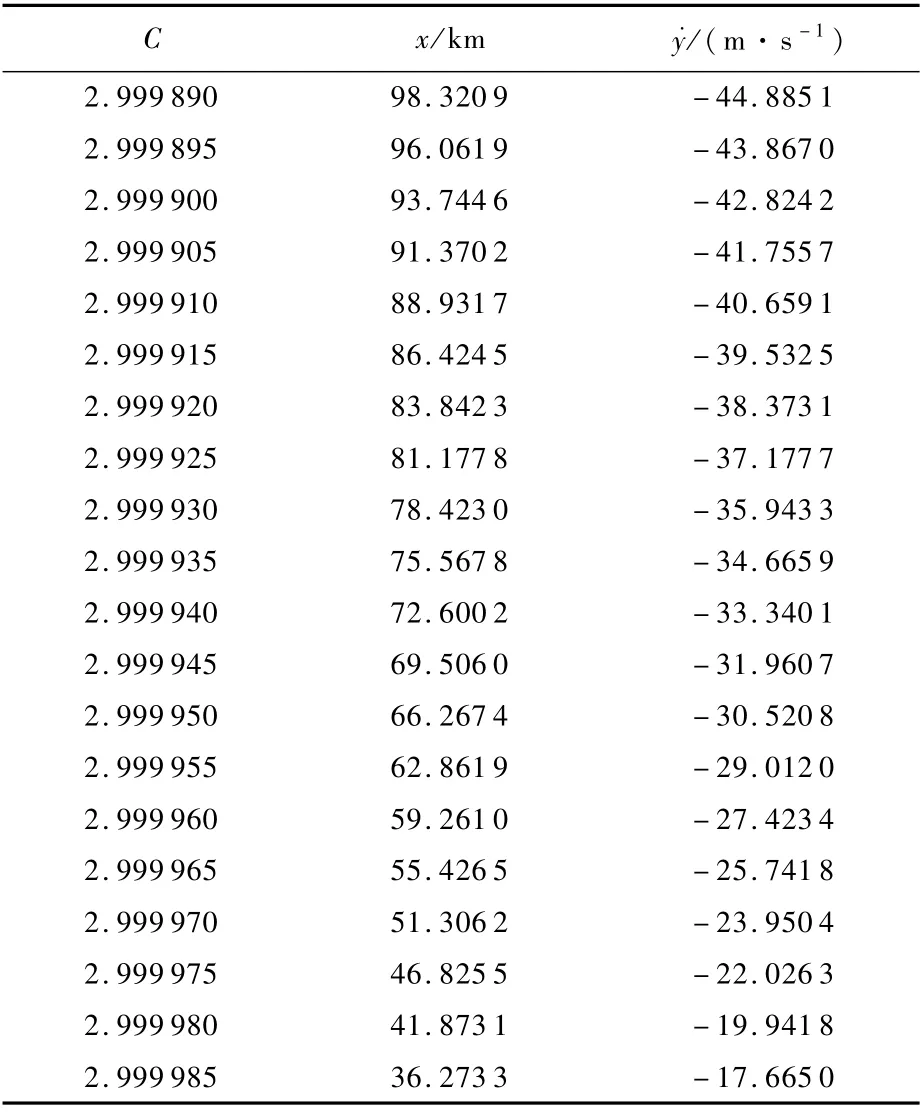
表1 不同Jacobi常数下周期准卫星轨道初始条件Table 1 Initial conditions of periodic QSOs w ith different Jacobi constants
图7中拼接边界以火卫一为圆心,以其Hill球半径的100倍为半径的圆,这个圆就是飞行器轨道的拼接临界面。图中的拼接边界内,飞行器轨迹是在以火卫一为质心的旋转系下绘制的,而在拼接边界外,轨迹是在惯性系下绘制的。当飞行器在拼接边界以外时,其距离火卫一引力影响球已经很远,火卫一引力作用可以忽略不计,飞行器的轨迹可以近似看作是一条环绕火星的Kepler轨道。反之,在拼接边界以内,则需要考虑火星与火卫一2个天体的引力。
当C=2.999 890,即入轨点距离火卫一质心98.320 9 km处时,取不同的ΔV,按本节所述方法对轨道进行反向仿真,可以得到施加不同速度脉冲时飞行器回溯轨道能够离开火卫一的最远距离,如图8所示。
在图8的关系曲线中取P1、P2、P3、P4、P55点,画出飞行器的回溯轨道如图9所示。
从图8中可以看出,回溯轨道离开火卫一的最远距离随速度脉冲的变化而发生跃变,且该跃变特性关于ΔV=0对称。定义回溯轨道依然稳定于火卫一附近的情况为稳定区(S),回溯轨道与火卫一距离过近或撞击火卫一的情况为表面起飞区(L),回溯轨道可以离开火卫一邻近区域的情况为入轨区(T)。定义各区之间的分界速度如图8所示:S区与L区分界VSL,L区与T区的分界速度为VLT和VTL。
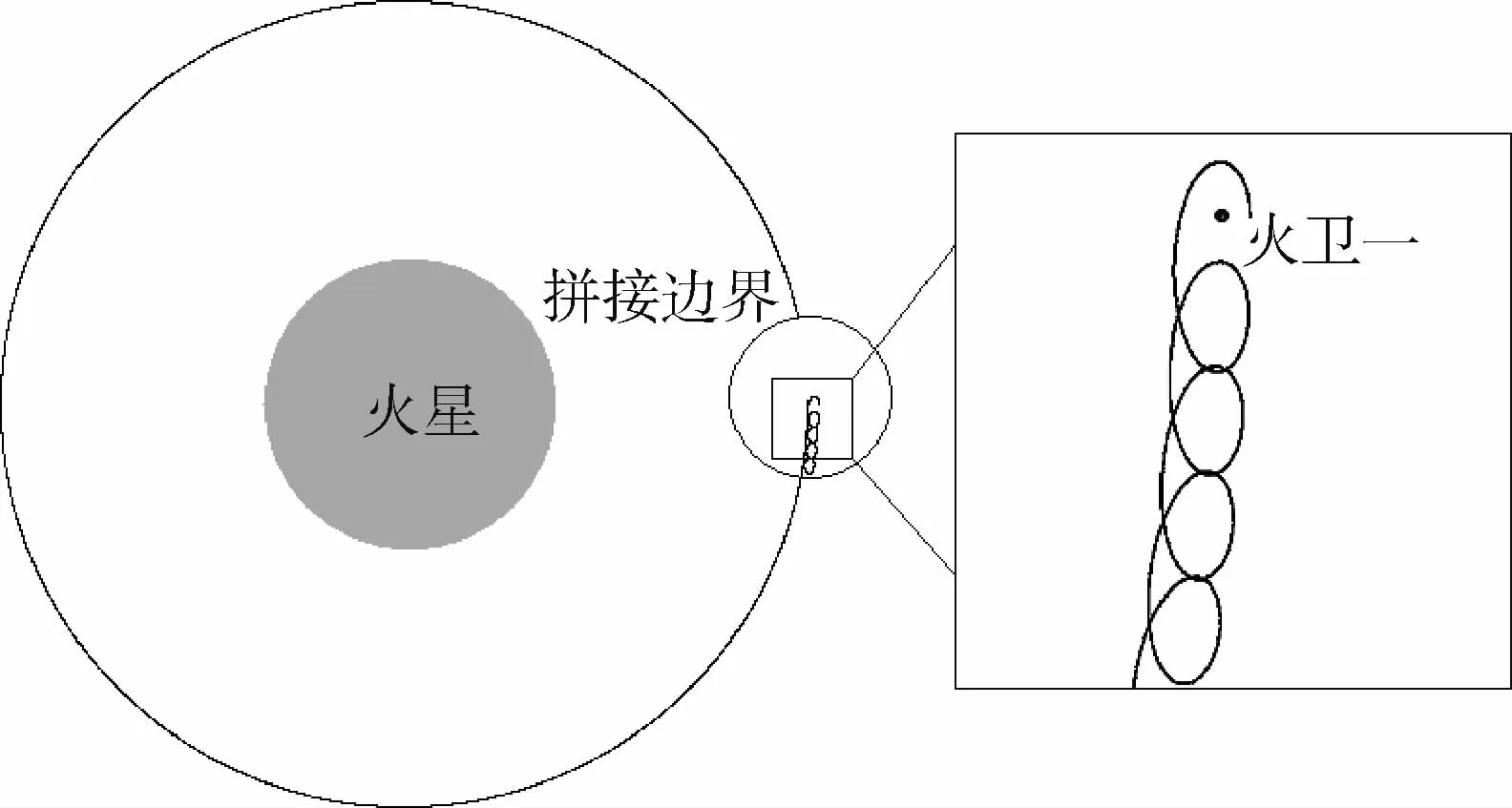
图7 火卫一周期准卫星轨道入轨Fig.7 Injection to a periodic QSO of the Phobos
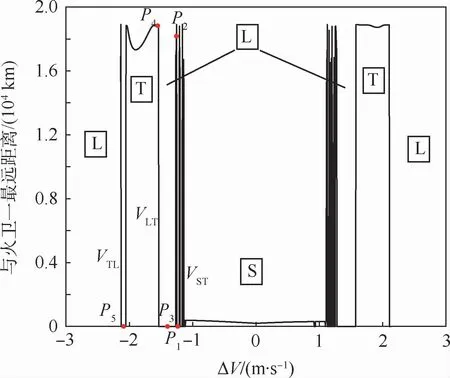
图8 不同速度脉冲ΔV时回溯轨道与火卫一的最远距离(C=2.999 890,x=98.320 9 km)Fig.8 Maximum distance from backward orbits to the Phobos with different impulsive velocity ΔV(C=2.999 890,x=98.320 9 km)

图9 P1、P2、P3、P4、P5 各点的回溯轨道Fig.9 Backward orbits on point P1,P2,P3,P4,P5
如图9所示,回溯轨道在远离火卫一过程中在y轴方向不断漂移,可能会撞击火卫一表面,如图9(a)、(c)和(e)所示。在撞击轨道之间,如图9(c)和(e)之间,存在可以避免撞击而成功远离火卫一的回溯轨道,如图9(d)所示。而在ΔV较小时,即图9(a)和(b)所在的区域,撞击与否对ΔV非常敏感,形成了一段尖峰区域,该区域撞击风险较大,在轨道设计中不应采用。如果对飞行器所施加的速度脉冲不加限制,可以给出足够大的速度机动,使飞行器有充足的动力反向逃离火卫一邻近区域,但是这种做法燃料消耗严重,很不经济。因此,在回溯轨道中剔除撞击火卫一之后的转移轨道,是可行且燃料消耗较小的选择。
飞行器在入轨前的运动状态,随着速度脉冲ΔV的变化如下:
1)当ΔV<VSL时,回溯轨道为环绕火卫一的拟周期准卫星轨道。
2)当VSL≤ΔV≤VLT或ΔV≥VTL时,回溯轨道与火卫一表面相交。
3)当VLT<ΔV<VTL时,回溯轨道可到达远离火卫一的区域。
飞行器的速度脉冲处于入轨区时,反向积分飞行器会离开火卫一,与火卫一的最远距离会达到19000 km左右,这个距离大约是火卫一轨道半长轴的2倍。这一点可以从准卫星轨道的特性得到解释:准卫星轨道从惯性空间上讲,是一条与火卫一半长轴相近的火星环绕轨道,受火卫一引力影响而可以稳定于火卫一的邻近空间。一旦飞行器离开火卫一邻近区域,弱化火卫一的引力影响,就会运行在一条与火卫一半长轴相近却不等的圆锥曲线轨道上。由于周期相近所以难以达到共振,经过一定时间的运动,飞行器与火卫一相对火星的相位差可达到180°,相互之间的距离也会达到火卫一半长轴的2倍左右。
由此,拼接边界的选择不会影响入轨速度脉冲与不同类型回溯轨道的对应关系,在选取时只要保证与火卫一距离足够远,且半径小于火卫一半长轴即可,本文取火卫一Hill球半径的100倍作为拼接边界。为了能够使用较少的燃料实现轨道转移,可以在入轨区(T区)速度脉冲中,结合任务的其他约束,酌情选择转移轨道。
选取入轨区P4点作为算例,反向积分入轨轨道,可以得到飞行器进行周期准卫星轨道入轨停泊轨道相对于火星的轨道要素如表2所示。
T区窗口的边界ΔV随Jacobi常数变化的情况如图10所示。图11给出了不同Jacobi常数下,由拼接边界进入相应周期准卫星轨道,选择T区的速度脉冲时,施加不同的ΔV所需要的转移时间,其中没有数值的部分表示回溯轨道稳定于火卫一附近或者回溯轨道与火卫一表面相交,无法完成轨道转移任务。

表2 入轨区P4 点入轨停泊轨道要素(相对火星)Table 2 Orbital elements of parking orbit for injection point P4(with respect to the Mars)
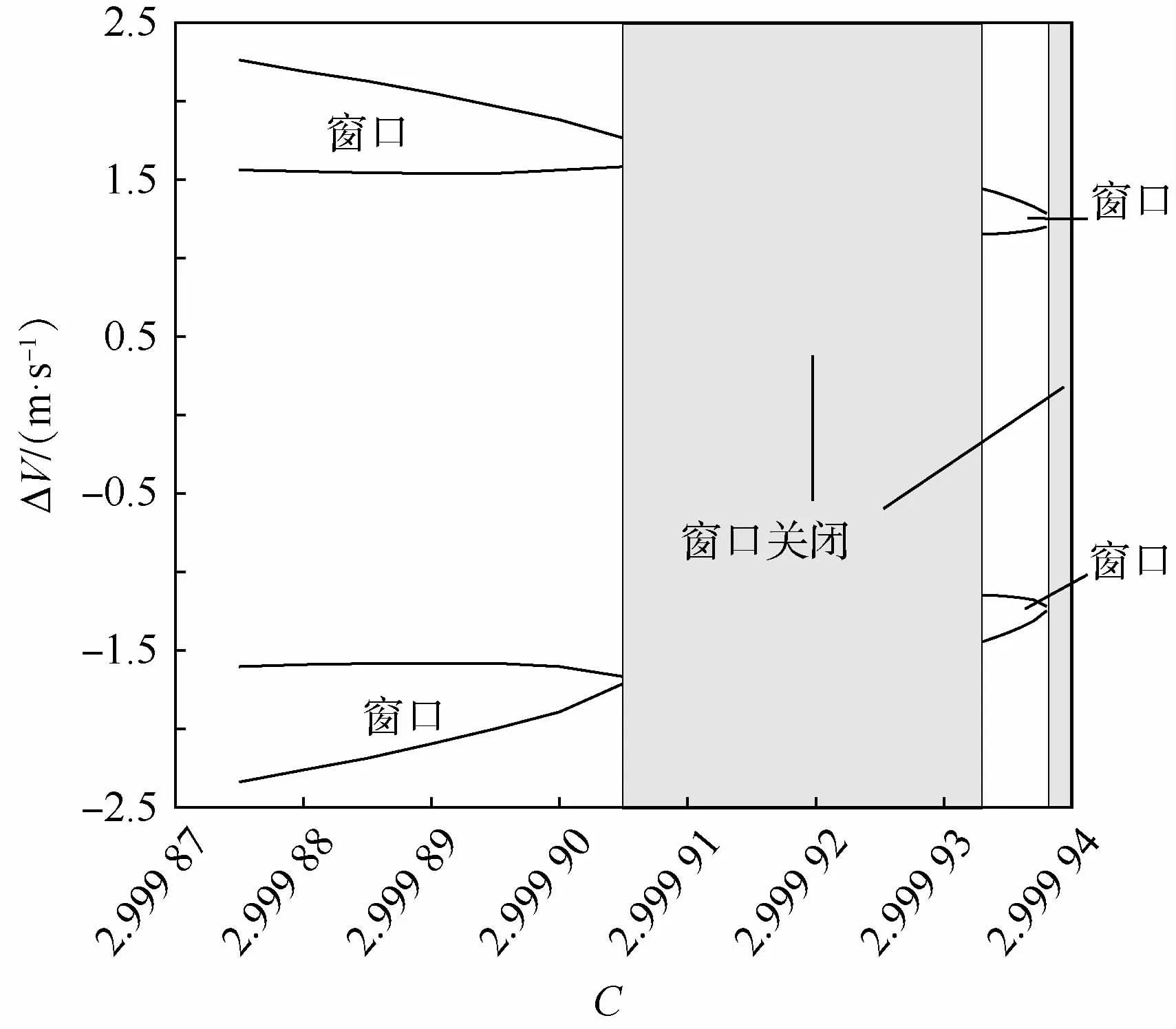
图10 不同Jacobi常数下的T区窗口分布Fig.10 T window distribution with different Jacobi constants
由图10可以看出,随着Jacobi常数增大,T区的转移窗口逐渐变小,直到2.999 905附近时完全关闭。在Jacobi常数介于2.999 905~2.999 933时,采取本文提出的转移方式撞毁的风险很大,因此认为此时T区关闭。在Jacobi常数增大到2.999 933时,T区窗口重新打开,直到Jacobi常数为2.999 938时,T区窗口再次关闭。随着Jacobi常数继续增大,飞行器进入了十分接近火卫一的区域,实现QSOs绕飞的难度和转移撞击到火卫一上的风险都大大增加,因此T区窗口保持关闭的状态。由此,为实现本文提出的转移策略,应当根据任务需要选择Jacobi常数小于2.999 905的周期准卫星轨道,或者选择Jacobi常数介于2.999 933~2.999938的周期准卫星轨道。
图11的结果显示,当给定周期轨道时,不同的Jacobi常数下,轨道转移时间随着脉冲速度的增加均呈现先增大后减小的趋势。因此,在设计特定周期轨道的转移时,需要根据任务的约束和可以实现脉冲的精度,在保证转移可以实现的前提下,在可选窗口中尽可能取较小值。
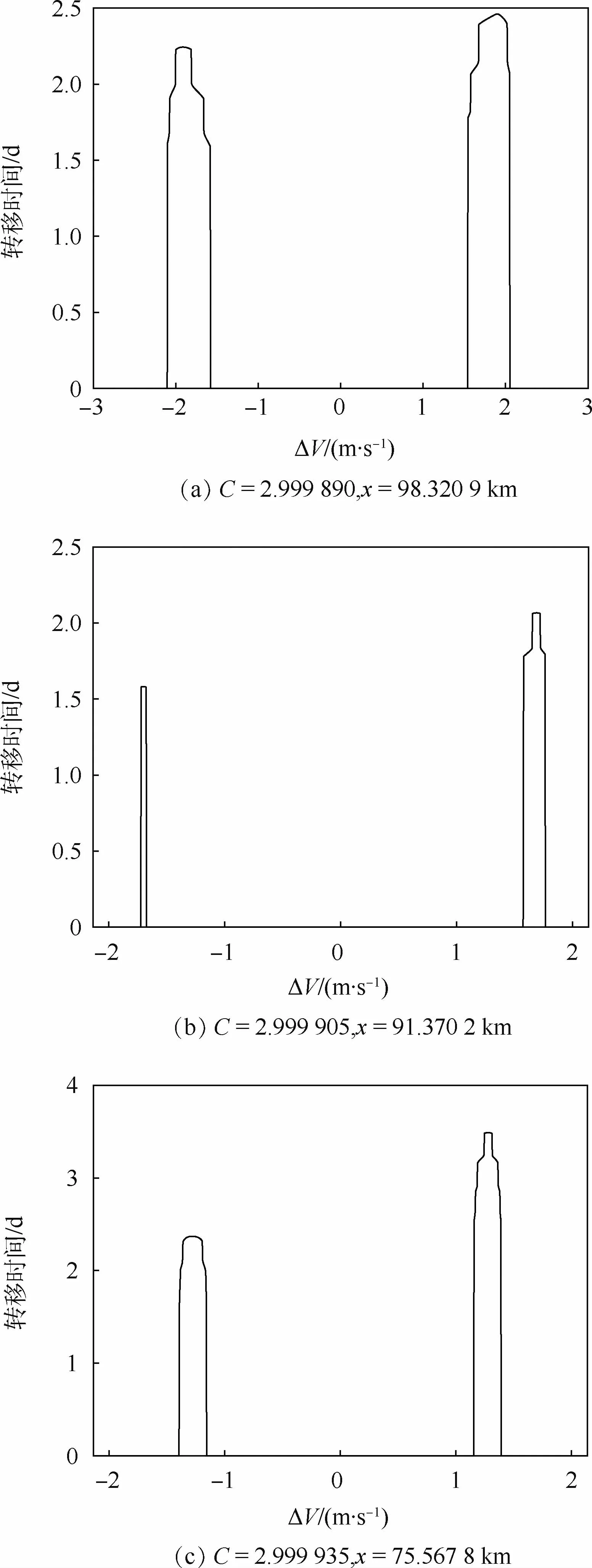
图11 不同Jacobi常数下,轨道转移时间与T区速度脉冲ΔV的关系Fig.11 Relationship between orbit transfer time and impulsive velocity ΔV with different Jacobi constants
基于上述分析可知,在本文设定的轨道转移方式下,对应特定的周期准卫星轨道,实现火星环绕轨道向火卫一周期准卫星轨道的转移,并可对燃料消耗和转移时间做出一定调整。
3 结 论
1)本文利用庞加莱截面方法分析火卫一邻近区域的准卫星轨道,发现准卫星轨道在庞加莱截面相空间上的稳定范围随Jacobi常数的减小而增大。对于控制精度有限的飞行器,应该选择Jacobi常数较小,距离火卫一较远的准卫星轨道作为任务轨道。
2)本文提出KAM环迭代法实现对周期准卫星轨道的数值求解,给出火卫一邻近区域的周期准卫星轨道族及其初始条件。
3)本文还提出一种从火星环绕轨道向火卫一周期准卫星轨道的转移轨道设计方法。分析这种轨道转移策略的时间和燃料消耗,发现周期准卫星轨道转移所需的速度脉冲可能存在特定的区间(T区),实现快速低能转移。T区的大小在一定范围内随周期轨道Jacobi常数增大而减小,随着Jacobi常数的增大,T区还会出现关闭的现象,但在Jacobi常数更高的区间内,当Jacobi常数处于特定的区间时,T区还会重新打开,形成新的窗口。应用本文中提出的方法,可以根据实际任务需要,设计合适的周期准卫星轨道,并找到燃料消耗较少,转移速度较快的转移轨道。
在进行转移轨道设计时,本文假设飞行器在庞加莱截面处进行轨道机动。实际上,轨道入轨点的选择会影响到轨道转移的能源与时间消耗。另外,飞行器在入轨点处入轨前的速度不一定相切于目标周期准卫星轨道,入轨机动的方向也可能被作为优化参数,用于降低整个转移过程的时间和能量消耗。在未来的研究工作中,笔者将从这些方面对转移轨道设计进行进一步的优化。

