基于HFSS的电源机箱屏蔽效能的仿真分析

张郑，冯成德

基于HFSS的电源机箱屏蔽效能的仿真分析

张郑，冯成德

（四川大学 机械工程学院，四川 成都 610065）

为减小电子仪器设备中电源模块之间电磁互扰，会给各个电源模块加上屏蔽机箱。而在实际中，箱体上通常会开设孔缝以便于散热和电子设备之间的连接，从而会产生电磁泄漏，导致屏蔽效能减小。因此，为了更好研究带孔缝电源机箱的屏蔽效能影响因素。在简单介绍了屏蔽效能的几种计算方法的基础上，通过与传输线法的对比，采用基于有限元法（FEM）的仿真软件HFSS对孔缝箱体进行建模仿真分析，探究孔缝的相关参数对屏蔽效能的影响规律，并据此对箱体的设计提出改进性建议。

屏蔽机箱；屏蔽效能；孔缝；HFSS；仿真分析

现代电子仪器设备的工作运行需要很多电源模块的支持，要集成各个电源模块就必须考虑电磁兼容（Electro Magnetic Compatibility，EMC）问题[1-2]，因此会给各个电源加上金属屏蔽机箱，进行电磁屏蔽，同时也能起到保护电源模块的作用。在电磁兼容的设计中，电磁屏蔽技术作为主要手段，近年来国内外对于箱体的电磁屏蔽特性做了一系列研究，但主要集中在箱体屏蔽材料的研发、屏蔽效能计算方法的优化、箱体对电磁波的耦合效应的研究等[3]。对孔缝的各类参数对箱体屏蔽效能的影响规律的探究还比较少。由于散热、电源信号线的传输、设备之间的连接等的需要，会不可避免地在屏蔽机箱开设各种孔缝，从而辐射的电磁波会通过孔缝耦合（后门耦合）[4]进入腔体内部，耦合到印刷电路板（PCB，Printed Circuit Board）上，对电路系统产生干扰，影响电源输出精度，直接影响整个电子设备的工作性能。因此研究带有孔缝的屏蔽腔体的电磁屏蔽效能对电子仪器设备具有重要的理论意义和应用价值。

1 屏蔽效能及其计算方法

屏蔽效能（SE，Shielding Effectiveness），单位为dB，用来定量评价机箱的屏蔽效果，定义为同一时间、地点，在空间上的某一点不加屏蔽体的场强0（0）与加入屏蔽体时的场强1（1）的比值，它表征了屏蔽体对电磁波的衰减程度[5]。表达式为：

机箱屏蔽效能的影响因素有：机箱材料特性、尺寸大小，机壳上的孔缝大小、数量、形状等，机箱内部的印刷电路板以及干扰电磁波的辐射频率、入射角度、极化方向等[6-7]。对于屏蔽效能的计算方法主要有数值法和解析法。常用数值法包括时域有限差分法（FDTD，Finite Difference Time Domain）、传输线矩阵法（TLM，Transmission-Line Matrix）、矩量法（MOM，Method of Moments）及有限元法（FEM，Finite Element Method）[9]。解析算法主要是基于平面波理论的传输线法[10]。数值法可用于计算不同形状、结构的物体，借助计算机可获取更高的求解精度[11-12]。所以这里采用基于有限元法的电磁场仿真软件Ansoft HFSS来分析孔缝的主要参数对机箱屏蔽效能的影响。

1.1 传输线法理论分析

Robinson M.P等[12]在TLM方法上进行拓展，建立了传输线理论模型，应用于屏蔽效能的求解。对于平面波垂直入射矩形腔体的情形，其实物模型及等效电路模型如图1、图2。

总体思路是将矩形腔体等效为一端短路的波导，并将开孔等效为左右两端短路的共面带状传输线。在图1中，显示电场垂直极化的平面波从空载腔体的开孔面垂直入射，结构体的各个参数在图中已给出，距离孔缝面的位置为腔体电压测试点。在图2中，以电压源0表示辐射源，其自由空间波阻抗为0，其值约为377 Ω，以等效电路中的点位置的电压来表示距离孔缝处的电场屏蔽效能。根据传输线理论，将矩形腔体等效为一端短路的波导结构，其阻抗为Z，传播常数为K。腔体前壁上的孔缝等效为左右两端短路的共面带状传输线，其等效阻抗为Z。

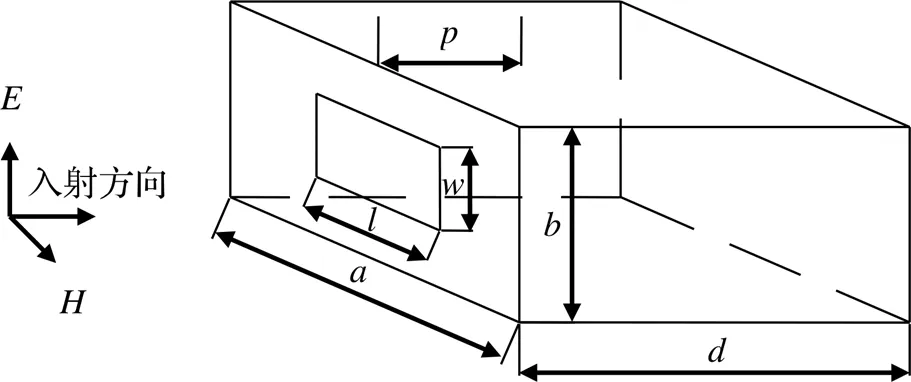
E、H为电场和磁场，一种垂直极化的电磁波；l、w为矩形孔的长宽；a、b、d为矩形腔体的长高宽

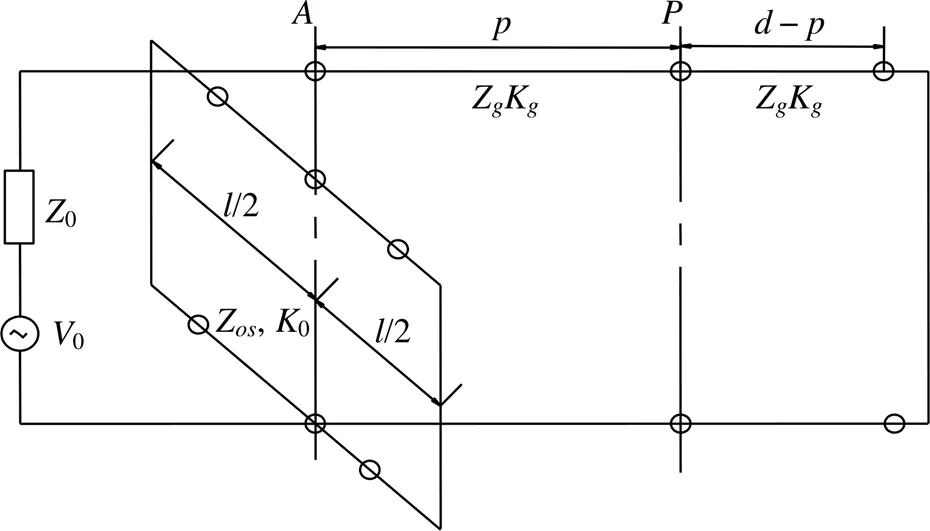
图2 等效传输线电路模型

根据Gupta[13]的理论，孔缝的特征阻抗可以表示为：

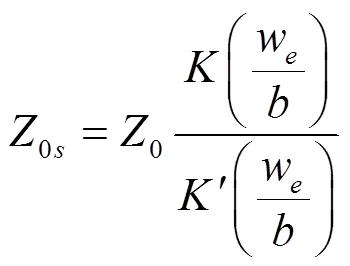
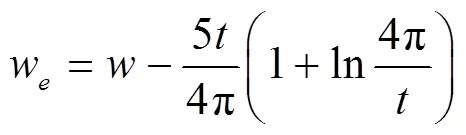
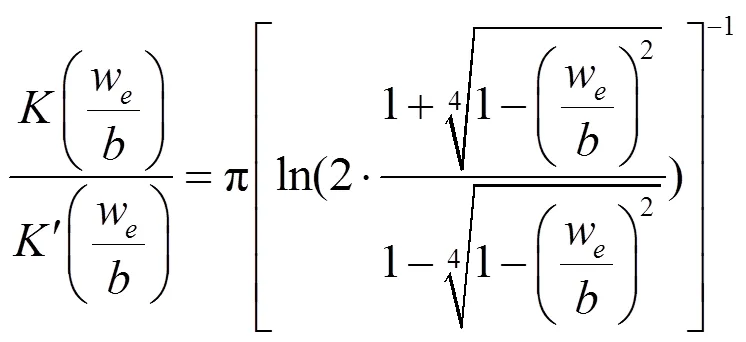
由式（1）～式（3）可得：

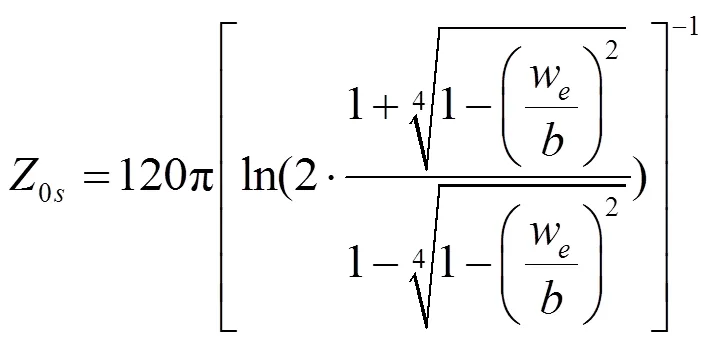
为了便于计算孔缝的等效阻抗Z，将两端短路的孔缝向中心处（点）做等效。此外，以/作为孔缝与屏蔽机壳之间的耦合因子，则可得孔缝的等效阻抗为：

在图2中，由0、0、Z形成并联的等效电路，由戴维南定理可得点的等效电压和等效阻抗为：

对于机箱上的孔缝，一般都是对称布置，所以电磁在矩形腔体中的主模为10，对于该种传输模式，波导的特征阻抗为：

传播常数为：

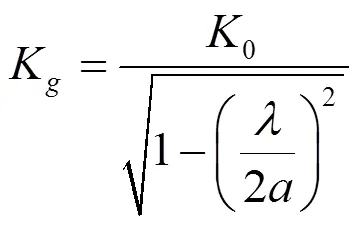
则可计算点的等效戴维南电压和阻抗为：

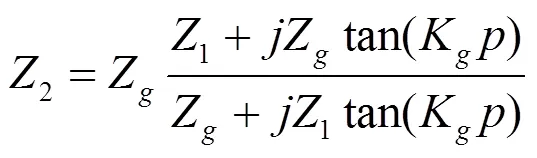
点的等效负载阻抗为：

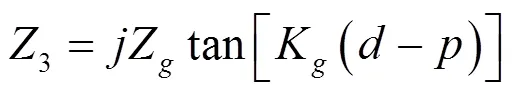
则测试点的等效电压和等效电流为：

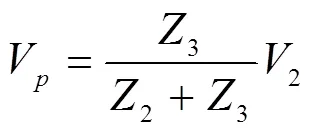
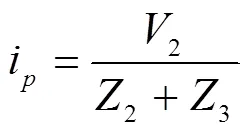
当没有矩形屏蔽机箱时，点的负载阻抗可近似为0，则其等效电压和等效电流分别为：

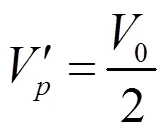
在传输线理论中，可用测试点电压、电流来表示屏蔽效能，则距离孔缝处的电磁场屏蔽效能可表示为：

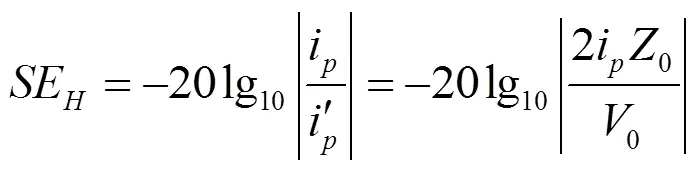
除此之外，需说明，以上公式推导是针对开矩形孔缝的屏蔽箱体。现在屏蔽机箱的开孔常见的还有圆形，对于圆形孔缝，根据Turner等提出的理论[14]，在面积相等的情况下，矩形孔缝和圆形孔缝屏蔽效能相同，则可以把公式中的孔缝的长宽改写为：

式中：d为圆形孔的直径。

等效确定孔缝长宽后就可代入后续公式，计算屏蔽效能。另外，如果是面上开有孔阵，则可将孔阵总阻抗视为单个孔阻抗的叠加。

1.2 两种方法对比

为了对比等效传输线法和基于有限元法的HFSS软件仿真两种方式计算屏蔽效能的结果，现进行HFSS建模仿真。机箱材料设置为铝，其尺寸选定为300 mm×120 mm×220 mm，箱体壁厚为1.5 mm。面上开有3×3的圆形孔阵，其半径为5 mm，如图3所示。

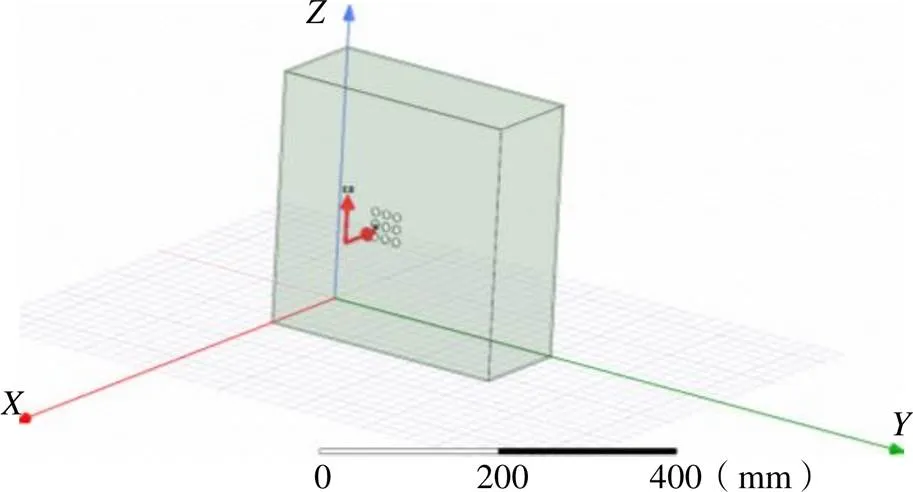
图3 仿真模型

激励源采用1 V/m的平面波0，采用电场垂直极化，从开孔面前方正中心40 mm处沿轴负半轴方向垂直入射，在HFSS的求解设置中，将平面波干扰源的扫频频率设置为0.1～1 GHz，步长为0.02 GHz，采用离散扫频类型。此外，需在箱体外围设置一空气盒子，边界条件设置为辐射边界，以此来模拟自由开放的辐射空间。屏蔽效能测试点为腔体中心。

另外，根据传输线法理论，运用MATLAB编程计算该箱体的屏蔽效能。两种方法的屏蔽效能如图4所示。

图4 两种方法计算结果对比

由图4可知，除个别频点，等效传输线法跟运用HFSS软件仿真计算箱体的屏蔽效能结果，基本一致，因此借助HFSS软件可便捷且较准确地计算不同开孔情况机箱的屏蔽效能。

2 含孔阵箱体屏蔽效能的探究

2.1 孔阵数量

HFSS中的箱体仿真模型尺寸和基本参数设定与前述一致，在开孔面上开设总面积为900 mm2的正方形孔阵，孔阵数量分别为1×1、3×3、5×5。孔间距为5 mm，如图5所示。

图5 孔阵数量示意图

分别仿真计算这三种模型的屏蔽效能，如图6所示。可以看出，在相同开孔面积的情况下，通过减小单个孔的尺寸大小、增加孔阵数量对屏蔽效能有明显提高。因此在实际的电子设备机箱中，散热孔都是开设成孔阵形式。但随着孔阵数量的增加，箱体的屏蔽效能增加幅度在减小，所以可以推测孔阵增加到一定数量后，其屏蔽效能会基本保持不变。

图6 不同数量孔阵屏蔽效能

2.2 孔阵间隔

为探究孔阵间隔大小对箱体屏蔽效能的影响，采用上述900 mm2的3×3方形孔阵，如图7所示。

dh.水平间隔 dv.垂直间隔

孔阵均匀分布，分别取d＝d＝10 mm、15 mm、20 mm，计算屏蔽效能，如图8所示，可看出，随着孔阵间隔的增大，除了在谐振点处，箱体的屏蔽效能只有小幅度提高。整体来说，屏蔽效能改善不大。所以在箱体表面设计散热孔阵时，在保证散热要求的情况下，可适当增加孔间距来减小相邻孔之间的互耦，改善屏蔽效能。但由于孔间距不可能远大于孔缝的最大线性尺寸，所以屏蔽效能的改善也比较有限。

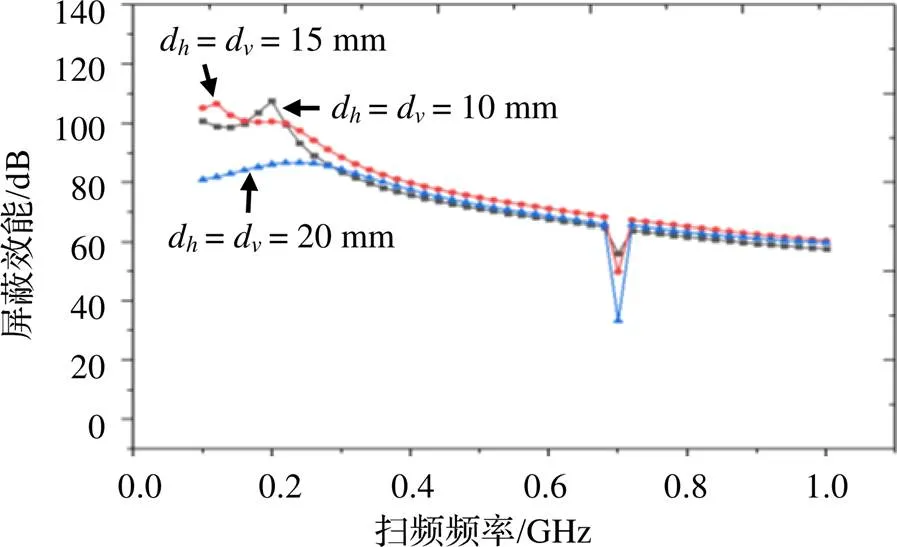
图8 孔阵不同间隔屏蔽效能

2.3 开孔尺寸

现通过改变矩形孔阵的长宽比来探究开孔尺寸对屏蔽效能的影响，如图9所示，开孔面积保持900 mm2不变。

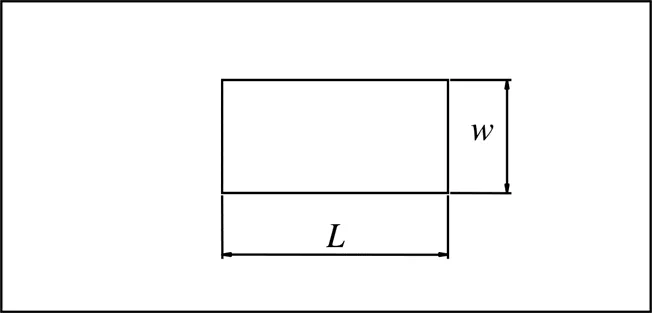
L.长边 W.短边

现取长宽比/分别为2、1.5、1计算其屏蔽效能。结果如图10所示。可以看出，在不同长宽比的开孔下，箱体的屏蔽效能随着激励源频率的改变其变化趋势大致相同。随着长宽比的增加，屏蔽效能逐渐减小。这说明，在开孔面积不变的情况下，开孔越狭长，电磁泄漏越严重，导致屏蔽效能越低。

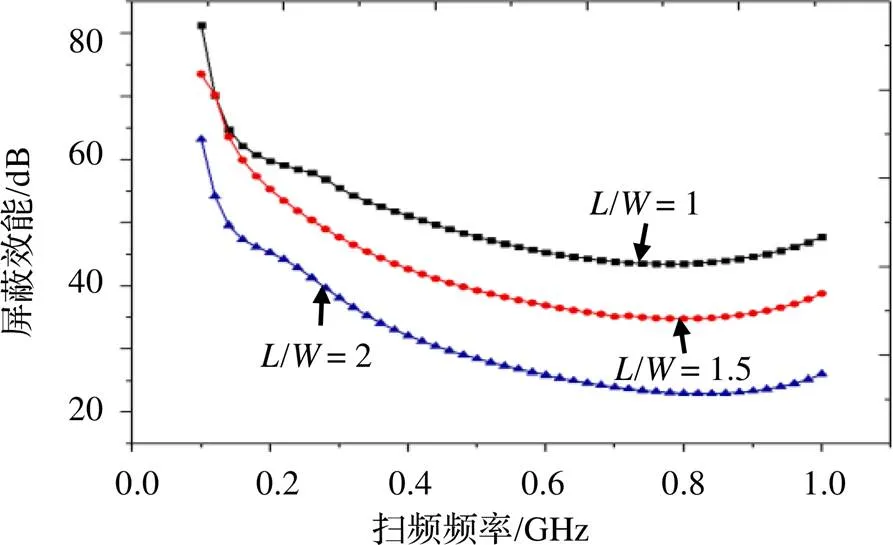
图10 开孔不同长宽比屏蔽效能

3 缝隙对屏蔽效能影响的探究

在实际的电子设备机箱中，由于不同部分的连接会存在一些缝隙，就势必影响箱体的导电连续性，造成电磁泄漏，影响其屏蔽效能。因此，有必要探究箱体缝隙的各个参数对屏蔽效能的影响。

3.1 缝隙长度

在距离箱体底部2 mm处开设一条长细缝，其长度分别为50 mm、100 mm、150 mm，宽度设为1 mm。如图11所示。

图11 缝隙长度示意图

对这三种长度的缝隙分别计算屏蔽效能，如图12所示。可看出，随着缝隙长度的增加，箱体的屏蔽效能逐渐降低。降低幅度逐渐变小。100 mm的缝隙比50 mm的缝隙屏蔽效能低约20 dB左右，150 mm缝隙比100 mm缝隙屏蔽效能低约10 dB左右。所以可以推测，当缝隙长度增加到一定数值时，屏蔽效能的减小趋于稳定。此外，缝隙长度没有改变腔体的谐振点。

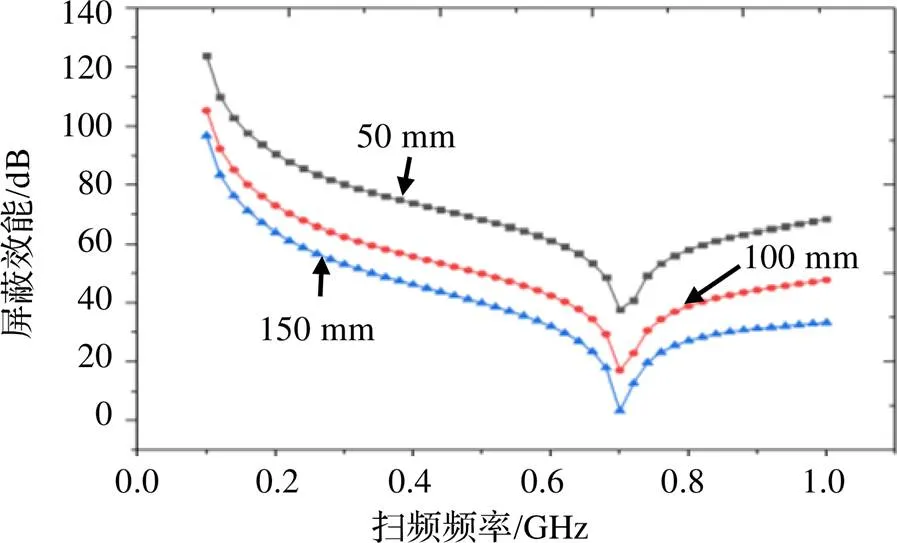
图12 不同缝隙长度屏蔽效能

3.2 缝隙数量

可分两种情况探究缝隙数量对屏蔽效能的影响。一是每段缝隙长度相等，均设为100 mm，数量不同，分别设置数量为1、2、3。宽度均设为1 mm，间隔设为2 mm，如图13所示。

图13 等长缝隙不同数量示意图

分别计算单缝、双缝、三缝的屏蔽效能，如图14所示。可看出，当长缝隙数量增加时，屏蔽效能有所下降，但幅度不是很大。最大下降幅度在10 dB左右，且下降幅度呈递减趋势。因此在设计屏蔽机箱时，可以根据设计需要增加或减少缝隙数量。

图14 等长缝隙不同数量屏蔽效能

第二种讨论的情况是，将同一长度的缝隙等分为多段。取总长为210 mm、宽度为1 mm的缝隙，将其等分为1、2、3段。其规格参数为210 mm×1、105 mm×2、70 mm×3，缝隙间隔设为2 mm。如图15所示。

图15 同一长度缝隙等分不同数量示意图

对图15三种开设方式的缝隙进行仿真计算其屏蔽效能，如图16所示。

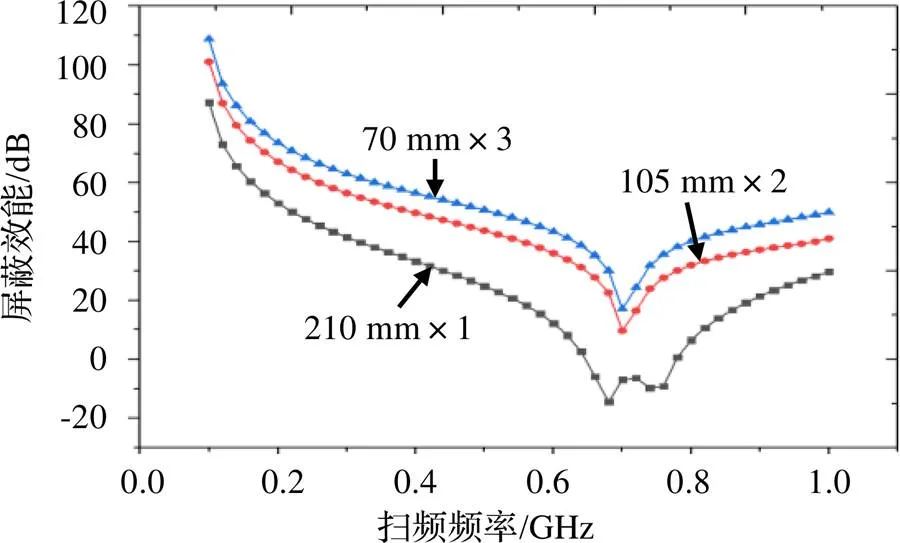
图16 等分不同数量屏蔽效能

从图16可以看出，在缝隙总长一定的情况下，单条缝隙布置的屏蔽效能最低，在谐振点附近其屏蔽效能甚至达到负值。而将缝隙等分布置可以提高箱体的屏蔽效能。其中，在缝隙二等分之后，箱体的屏蔽效能提升了约20 dB，三等分之后又提升了10 dB左右。因此，在设计屏蔽机箱时，在满足结构设计要求的前提下，可以将箱体上开设的缝隙等分为多段布置，可以有效地提高其屏蔽效能。

3.3 缝隙间隔

为探究缝隙间隔对箱体屏蔽效能的影响，在仿真箱体模型的面上开设双缝，缝隙长度为100 mm，宽度为1 mm。双缝之间的分别设置不同的间隔，如图17所示。

分别对图17所示的三种缝隙位置进行仿真计算，如图18所示。可以看出，三种位置间隔的屏蔽效能差异比较明显，其中位置1和位置2缝隙开设的间隔虽然差别较大，但除了个别频点，两种间隔屏蔽效能大致相同。位置3的缝隙对称分布在开设面的两侧，其屏蔽效能比前两种位置大很多。因此可以推断在设计屏蔽机箱时，若需要增大缝隙间隔来提高屏蔽效能，就要考虑缝隙在开设面上布置的对称性。

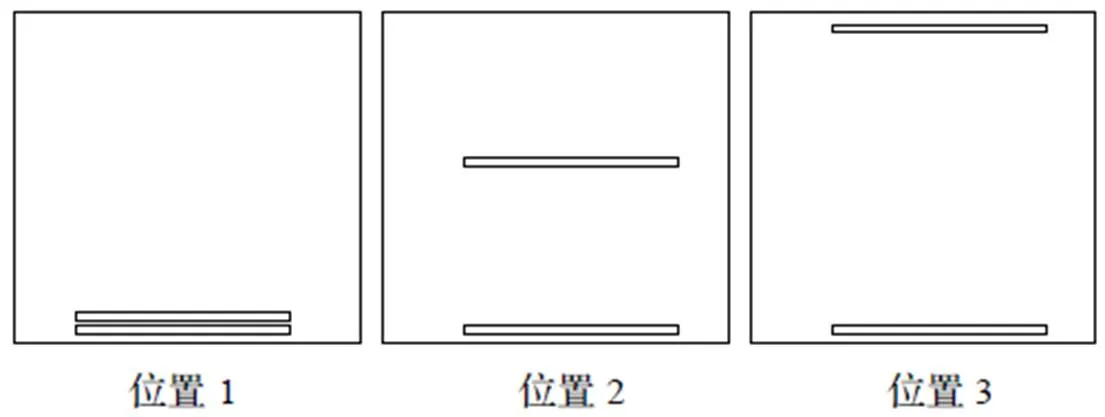
图17 缝隙不同间隔位置示意图

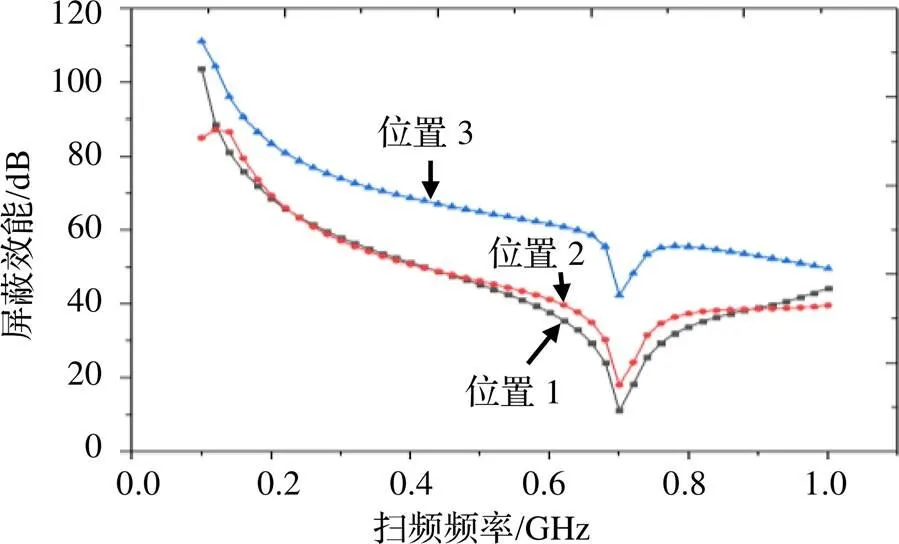
图18 缝隙不同间隔位置屏蔽效能

4 结束语

本文对电源屏蔽机箱的屏蔽效能做了一定探究。提出的传输线法和HFSS仿真的结果基本吻合，因此采用HFSS软件对孔缝箱体的屏蔽效能计算分析，得出以下结论：

（1）在开孔面积相同的情况下，孔阵数量越多，屏蔽效能越高。所以在设计机箱时在保证散热的情况下，可以减小单个孔的面积，增加孔阵数量来提高屏蔽效能；孔阵间隔大小对屏蔽效能影响并不显著；对于矩形孔，开孔长宽比越小，屏蔽效能越高。

（2）对于箱体上开设有狭长缝隙的情况，缝隙长度越长，数量越多，屏蔽效能越低；同一长度的缝隙，等分布置数量越多，屏蔽效能越高；缝隙间隔对屏蔽效能影响并不大，但缝隙在开设面上的对称性会影响屏蔽效能。

利用HFSS软件可以快捷且准确对箱体屏蔽效能的影响参数进行仿真分析，从而对电源屏蔽机箱的设计具有指导作用。

[1]周泽伦. 带孔缝箱体电磁屏蔽效能的研究[J]. 西安科技大学学报，2016，36（1）：122-126.

[2]郭超. 基于HFSS在有孔矩形金属腔体中电磁屏蔽效能的应用[J]. 科技视界，2015（18）：84-85.

[3]陈新平，杨显清. 基于HFSS的有孔屏蔽体的屏蔽效能分析[J].信息技术，2012，36（10）：140-143.

[4]何林涛. 基于HFSS的孔阵机壳近场屏蔽效能分析[J]. 工程设计学报，2011，18（4）：255-259，292.

[5]范丽思，周星，潘晓东. 基于箱体法材料电磁脉冲场屏蔽效能测试研究[J]. 微波学报，2017，33（3）：22-27.

[6]周金山，刘国治，王建国. 矩形孔缝耦合特性实验研究[J]. 强激光与粒子束，2003，15（12）：1228-1232.

[7]赵蒙，达新宇，张亚普. 任意方向平面波入射下有孔箱体屏蔽效能的估算[J]. 微波学报，2015，31（4）：72-77.

[8]David A. Hill，Mark T. Ma，Arthur R. Ondrejka，et al. Aperture Excitation of Electrically Large, Lossy Cavities[J]. IEEE Transactions on Electromagnetic Compatibility，1994，36（3）：169-178.

[9]张强. 金属屏蔽腔体的孔缝微波耦合特性研究[D].西安：西安电子科技大学，2014.

[10]崔杨. 矩形金属腔体屏蔽效能分析[D]. 西安：西安电子科技大学，2011.

[11]吴贤. 电子设备机箱的电磁屏蔽特性研究[D]. 成都：电子科技大学，2011.

[12]Robinson M P，Turner J D，Thomas D W P，et al. Shielding effectiveness of a rectangular enclosure with a rectangular aperture[J]. Electronics letters，1996，32（17）：1559-1560.

[13]单锦辉，王戟，齐治昌，等. Gupta方法的改进[J]. 计算机学报，2002（12）：1378-1386.

[14]J. D. Turner，T. M. Benson，C. Christopoulos，D. W. P. Thomas，M. P.Robinson，J. F. Dawson，M. D. Ganley，A. C. Marvin，and S. J. Porter. Characterization of the shielding effectiveness of equipment cabinets containing apertures[J]. inInt. Symp. EMC, Rome，Italy，Sept. 1996：574-578.

Simulation Analysis of Shielding Effectiveness of Power Supply Case Based on HFSS

ZHANG Zheng，FENG Chengde

(School of Mechanical Engineering, Sichuan University, Chengdu 610065, China )

In order to reduce electromagnetic interference generated between power supply modules in electronic equipment, a shielding case is used for each power supply module. Shielding effectiveness of the case will directly affect the performance of the electronic device. The case usually has holes in it for heat dissipation and for the connection between electronic equipment, which will cause electromagnetic leakage and reduce shielding effectiveness. In order to study the shielding effectiveness of power supply case with slot, this paper briefly introduce several calculation methods of shielding effectiveness. By comparison with transmission line method, the finite element method (FEM) -based simulation software HFSS is used to model and analyze the case. The influence of the related parameters of the slot on the shielding effectiveness is studied and suggestions are made to improve case design.

shielding case；shielding effectiveness；slot；HFSS；simulation analysis

TN98

A

10.3969/j.issn.1006-0316.2020.07.006

1006－0316 (2020) 07－0035－07

2020－01－02

四川省科技计划项目（重点研发项目）（2020YFN0010）

张郑（1994－），男，重庆人，硕士研究生，主要研究方向为电磁兼容设计，E-mail：1121977916@qq.com；

冯成德（1962－），男，江苏启东人，硕士，副教授，主要研究方向为机电工程、机器视觉、数字图像处理。