整体壁板压弯成形的形状控制

张敏，田锡天，李波

西北工业大学 机电学院，西安 710072

随着航空航天工业数字化设计及制造技术的快速发展，对现代飞行器的性能要求不断提高，飞机设计结构发生了变化，开始大量采用整体结构设计，如整体框、梁、壁板等零件[1]。以铝合金材料为主导的大型整体壁板是构成飞机气动外形的重要组成部分，同时也是机翼、机身等的主要承力构件，因具有减重效果明显、总体和局部刚度好、强度高等优点[2-3]，在航空航天等领域获得了广泛的应用。

作为飞机最大的承载部件，现代大型飞机机翼翼盒的结构设计也采取了整体壁板的结构形式。此类壁板将机翼蒙皮与长桁、肋、对接接头以及其他可附带的结构件(如注油口框等)集合为一体[4]，大大减少了结构零件的项目和数量。但是由于此类壁板结构复杂，尺寸变化较大，外形精度要求高，如何成形是整机研制过程中必须解决的关键技术之一。

压弯成形(指增量压弯成形)是由专用压力机驱动压头在整体壁板表面按一定的路径分段逐点进行局部三点弯曲变形，最后使整个壁板表面弯曲为所需型面的成形工艺，其基本原理是靠逐次的变形累积产生整体的变形[5]，如图1所示，具有设备工装简单、变形力大、生产周期短和对外形曲率适应性强等特点，是带筋整体壁板的局部弯曲成形，或带有加厚横向凸台和口盖周围的加强区及高筋条整体壁板的一种重要成形手段[6]。机翼整体壁板中厚度尺寸较大的对接接头部分的成形就采用压弯成形方法。但压弯成形是一个十分复杂的弹塑性变形过程，卸载后伴随着不同程度的回弹，导致压弯成形质量难以保证和控制[7]，如对于复杂的铝合金壁板，需要6个多月进行回弹误差校正[8]。通过对飞机制造企业现场的调研证实：由于整体壁板压弯成形方面缺少必要的科学理论和技术指导，工程实际中只能依靠操作者的经验和技术水平，采用“试探法”“变压边量”“局部校形”等手段获得理想外形，导致现有压弯成形精度低，严重影响飞机的装配质量和效率。

图1 压弯成形原理Fig.1 Press bend forming principle

目前，对压弯成形形状控制的研究主要有工艺控制和模面补偿两种方法[9]。工艺控制是通过调整凸模下压量[10]、增加成形步骤[11-12]、提高成形温度[13]等方式控制成形形状，能够在一定程度上减小回弹，但无法彻底消除。模面补偿中应用较为成熟的是节点位移调整(Displacement Adjustment, DA)[14-17]方法，DA法是基于有限元模拟技术的闭环迭代法，通过修正模具型面进行回弹补偿，获得理想的零件成形精度，具有收敛性好、速度快和通用性强等优点，主要适用于采用模具成形的零件。

对于分段逐点三点弯曲成形的形状控制研究，岳峰丽等[18]通过大量实验建立了增量压弯成形中压下量和弧高值的一元线性回归模型，实现了实际加工时工艺参数的初选，然后在压弯过程中通过实时检测理论弧高值和实测弧高值的误差调整特征方程，保证成形精度。付泽民等[19]通过采用Abaqus有限元方法调整板材料多道次渐进折弯成形中各道次的模拟工艺参数，实现大尺度U形工件的精确成形。上述方法依然是依据经验进行参数调整或者基于仿真进行参数调整。Yan等[20]建立了各压点处下压量与成形误差的神经网络模型，通过采用遗传算法优化BP神经网络的方法，获得各压点处最优的下压量。但该方法仅适用于成形特定的曲率半径，当曲率半径发生变化时，需要重新建立神经网络模型。

在上述研究的基础上，基于弹塑性变形理论和几何分析建立了压弯成形局部变形下压量预测模型，基于有限元法建立了压弯成形整体变形有限元仿真预测模型；综合考虑压弯成形局部-整体变形精度，利用模具型面迭代思想(DA法)和逐步逼近思想，构建了压弯成形轮廓曲线迭代模型。以Abaqus为平台，对压弯成形形状控制方法进行验证，为整体壁板压弯精确成形提供理论指导。

1 整体壁板压弯成形形状控制方法

1.1 压弯成形整体变形控制原理

通过文献[21]可知，对于压弯成形过程，即使有很精确的预测模型，也需要一定的反馈获得目标成形形状。因而，仍需通过迭代补偿获得目标成形曲线及其对应的下压量大小。压弯成形整体变形控制迭代原理如图2所示。将弯曲线上相应节点处的位移作为调节变量，每个点的调节变量是一个二维矢量。当用来作为形状补偿的节点越多时，补偿精度越高，但过多的节点会造成计算量过大。

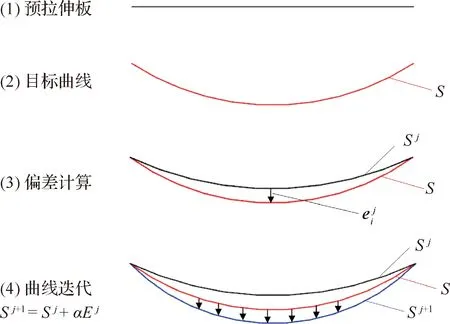
图2 迭代原理Fig.2 Iteration principle

1≤i≤m, 1≤j≤m

(1)

压弯成形时，首先计算控制节点与目标形状之间的偏差，压弯成形后对偏差进行补偿。如对第j次成形后壁板形状Sj进行补偿，则第j+1次成形后壁板外形形状为Sj+1，即

Sj+1=Sj+αEj1≤j≤m

(2)

式中：m为节点数量；α为补偿因子，用以减小偏差补偿量防止过弯，通常取0.7～0.9[17]。当成形后形状偏差在允许误差范围内时，迭代补偿结束。

1.2 压弯成形整体变形控制过程

为了对压弯件的成形精度进行评价，需要对压弯件的成形精度进行定量计算。由于压弯件外形轮廓为曲线，因此采用实际成形曲线与目标曲线之间的偏差作为成形精度，即按照一定距离提取成形曲线上的若干节点，所有节点与目标曲线节点之间距离的均方根作为整体偏差评价指标，用于控制整体变形，节点之间最大距离作为局部偏差评价指标，用于控制局部变形。当整体偏差和局部偏差均小于给定误差值，则精度满足要求。具体描述为

(3)

式中：Δli为节点与成形件目标曲线之间的距离；ξ、ζ为允许误差。

根据压弯成形形状控制原理，提出压弯成形形状控制过程如图3所示，主要分为两步：第1步将压弯成形局部变形解析预测得到的下压量作为有限元分析的初始边界条件，然后进行有限元计算；第2步以评价指标作为目标函数，结合补偿因子更新参数值并将更新后的值返回到Abaqus中，直到精度满足要求，停止迭代获得最优下压位移量。

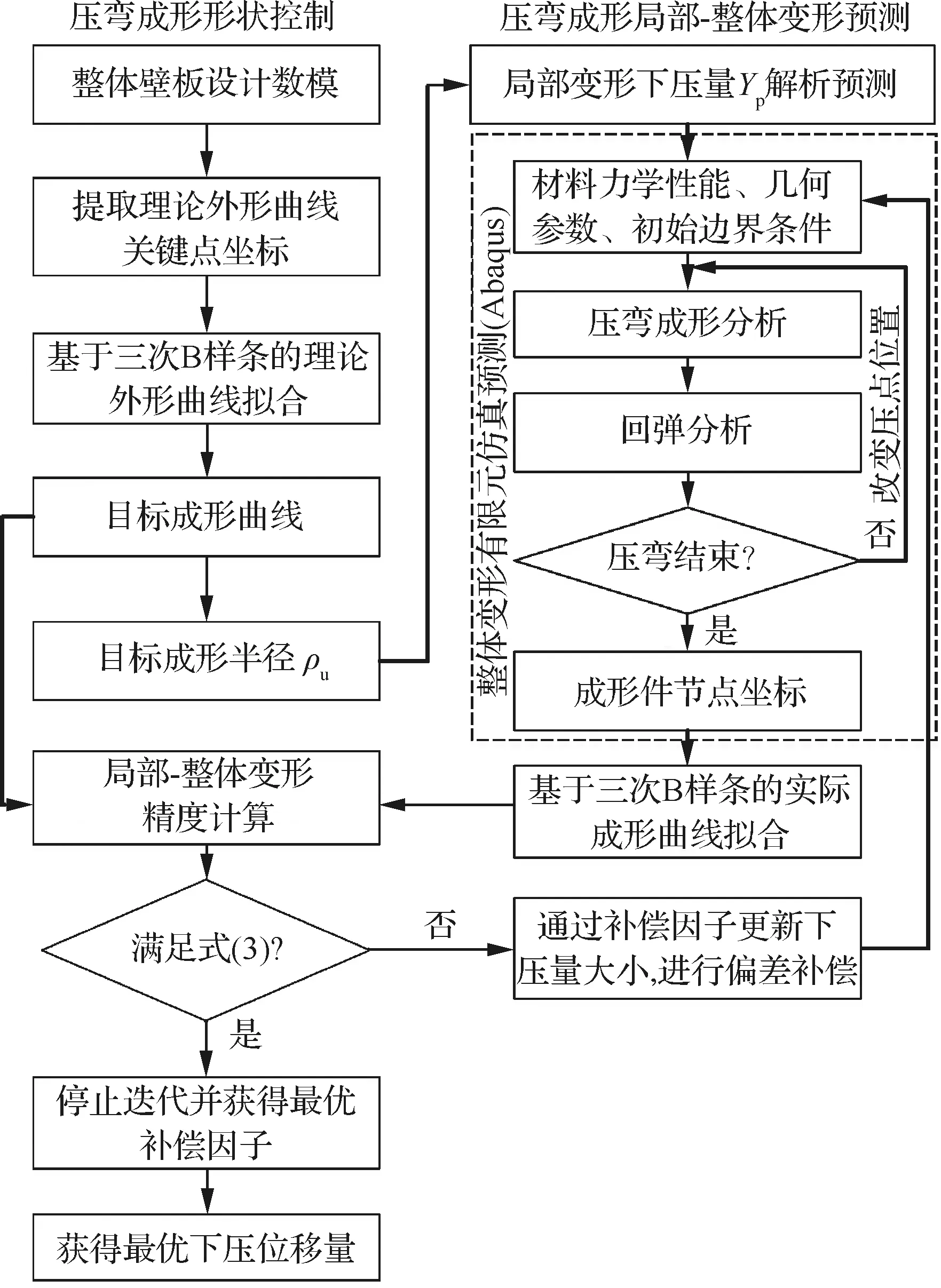
图3 压弯成形形状控制过程Fig.3 Shape control process of press bend forming

2 整体壁板压弯成形局部-整体变形预测

2.1 整体壁板试件设计

为方便在实验室进行实验，需设计整体壁板缩比试件模型。结合几何相似性并根据实际机翼整体壁板，如图4(a)所示，设计整体壁板缩比试件模型，如图4(b)所示，整体壁板试件由对接接头(即图中所示的压弯成形区域)和筋板两部分组成，试件几何尺寸为200 mm×60 mm×7.5 mm。

图4 整体壁板试件Fig.4 Specimen of integral panel

2.2 材料模型

航空广泛使用的7050-T7451铝合金材料属于高强度热处理铝合金，具有极高的强度和良好的耐磨性，主要用于制造飞机结构件，如飞机上、下翼面壁板、桁条等。单拉实验是测定材料力学性能的基本实验。根据国家标准GB/T228—2002《金属材料 室温拉伸实验方法》设计拉伸实验样件，在CSS-44100电子万能实验机以1.5 mm/min 的速度进行单拉实验，如图5(a)所示。通过求取三组实验的平均值，获得材料工程应力-应变曲线，考虑变形过程中试件截面面积的改变，将工程应力-应变曲线转换为真实应力-应变曲线，如图5(b)所示。材料力学性能如表1所示。

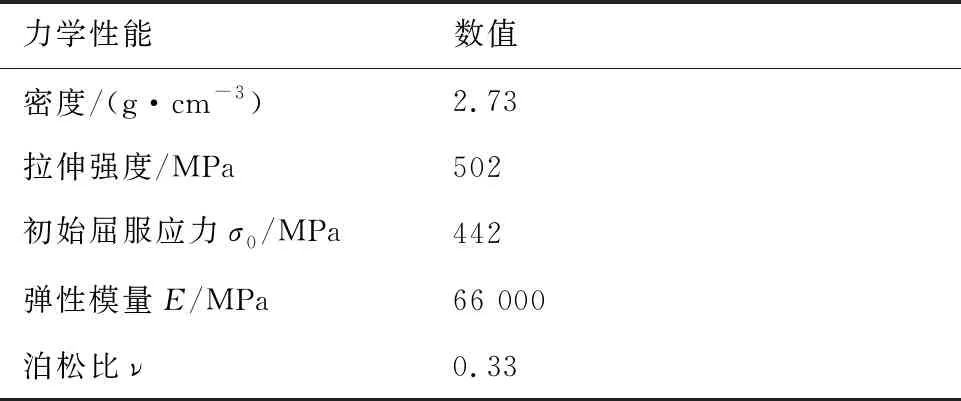
表1 7050-T7451力学性能Table 1 Mechanical properties of 7050-T7451

表2 硬化参数Table 2 Hardening parameters

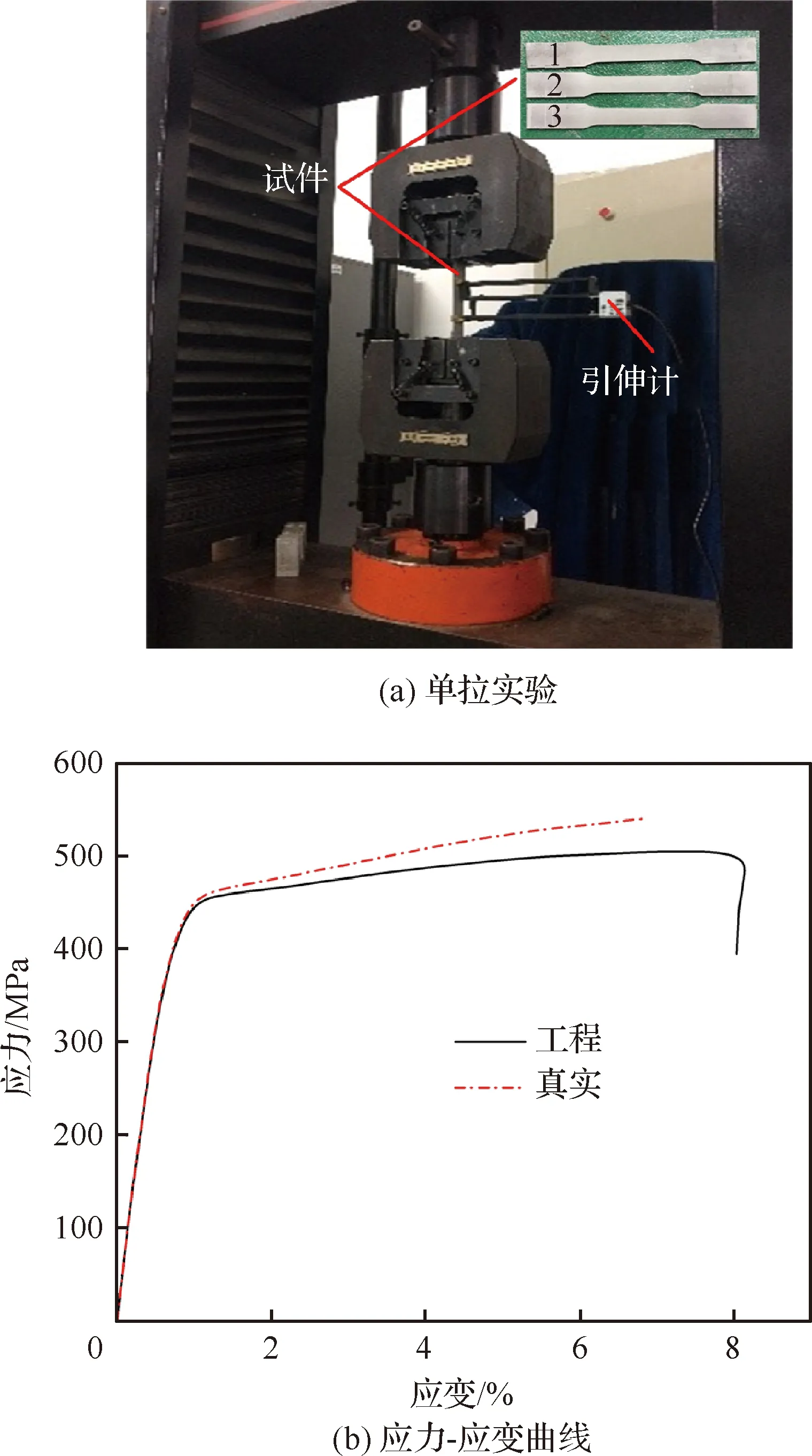
图5 7050-T7451铝合金应力-应变曲线Fig.5 Stress-strain curves of 7050-T7451 aluminum alloy

将不同硬化模型拟合得到的单拉应力-应变曲线与实验数据进行对比，如图6所示。从图中可以看到，Ludwik硬化模型和H-S硬化模型的拟合效果相近，但Swift硬化模型拟合结果更接近于单拉实验应力-应变曲线。因此，选择采用Swift硬化模型。

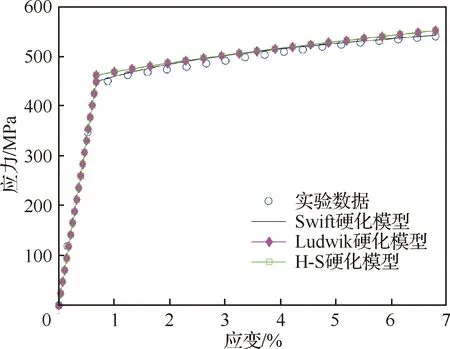
图6 实验和不同硬化模型得到的单拉应力-应变曲线Fig.6 Uniaxial tensile stress-strain curves obtained from experiments and different hardening models

2.3 整体壁板压弯成形局部变形下压量解析预测

根据压弯成形原理，从局部变形和整体变形的角度对压弯成形过程进行研究。理论解析法适用于分析局部三点弯曲变形这类简单约束条件下的弯曲成形问题。因此，为了对整体壁板局部变形下压量进行解析预测，将筋板部分简化，以接头部分截面作为受力截面。当下压量为Yp时，压弯成形局部变形如图7所示。

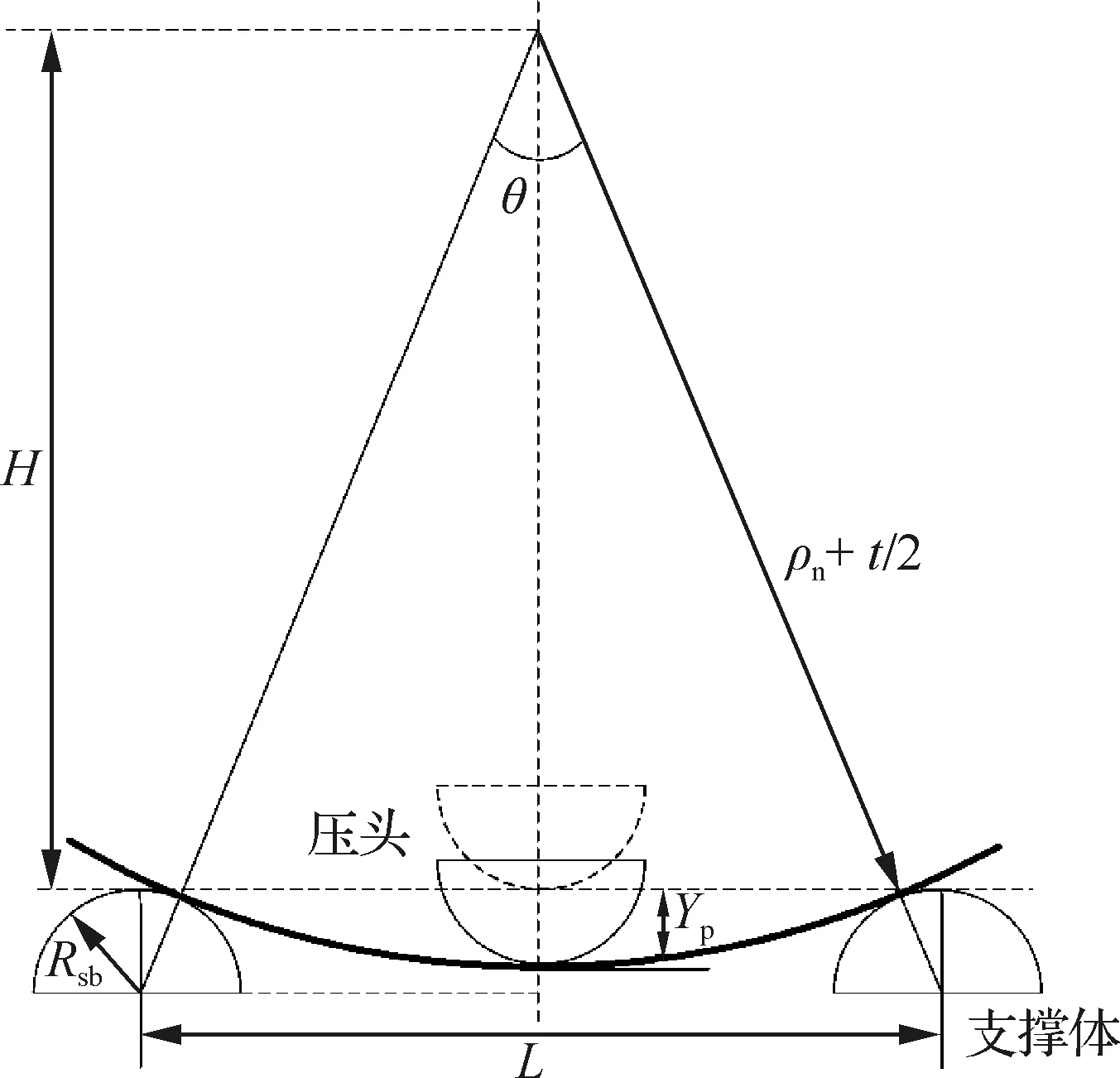
图7 下压量与成形半径Fig.7 Punch displacement and forming radius

通过几何分析，可得：

(4)

式中：θ为卸载前的弯曲角；L为支撑体之间的跨距；ρn为卸载前中性层成形半径；t为板料厚度；Rsb为支撑体半径。

对式(4)采用三角函数平方关系进行变换，求得图7中H的表达式为

(5)

下压量Yp与成形半径ρn之间的几何关系为

Yp=ρn+t/2-H

(6)

将式(4)代入式(5)，联合式(6)，得到下压量的表达式为

(7)

基于经典回弹理论，弹塑性曲率变化等于弯矩引起的弹性曲率的变化，即回弹弯矩与加载弯矩在数值上相等，方向相反。因此，回弹后曲率变化为[22]

(8)

式中：ρu为卸载后中性层曲率半径；M为压弯成形局部变形时压头下方截面内弯矩；I为截面惯性矩，计算公式为I=ωt3/12(ω为截面宽度)。

由式(8)获得ρu与ρn的关系为

(9)

式中：ρn为获得目标成形半径所需要的卸载前局部成形半径；ρu可以理解为目标成形半径。

将式(9)代入式(7)，可以得到目标成形半径ρu与下压量Yp之间的关系为

(10)

式中：弯矩M可以通过式(11)积分获得，

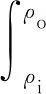
(11)

式中：ρo和ρi分别为弯板最外侧和最内侧的曲率半径；ρ为截面上一点的曲率半径；σθ为切向应力，随着采用的材料应力-应变关系的不同而具有不同的表达式。基于Swift硬化模型推导压弯成形弹塑性区域切应力表达式为[23]

1) 弹性区域(ρn-ye<ρ<ρn+ye)：

(12)

2) 弯板内侧塑性区域(ρi≤ρ≤ρn-ye)：

(13)

3) 弯板外侧塑性区域(ρn+ye≤ρ≤ρo)：

(14)

式中：ye为弹塑性分界面到中性层的距离。

由式(10)～式(14)，下压量Yp与目标成形半径ρu、板料厚度t、支撑体半径Rsb、跨距L及材料参数ν、E、K、n相关。在材料、板料厚度t、支撑体半径Rsb和跨距L一定时，下压量Yp只与目标成形半径相关。通过数值迭代法计算获得目标成形半径所需要的下压量大小的计算流程如图8所示。先给定成形半径的初始值，通过迭代计算直到获得的成形半径满足目标成形半径的误差要求，即可计算得到获得目标成形半径的下压量大小。

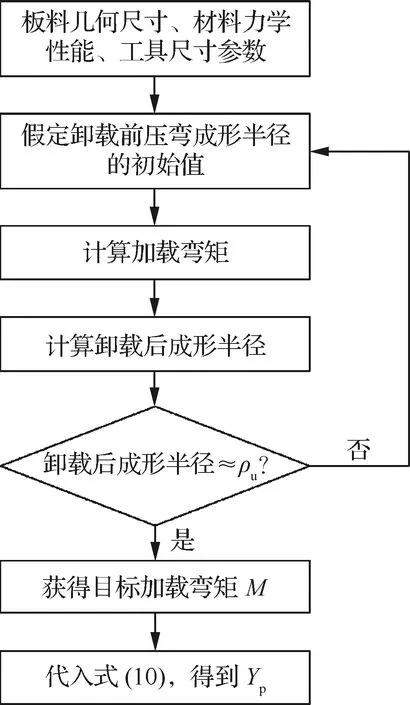
图8 局部变形下压量计算流程Fig.8 Flowchart of punch displacement calculation of local deformation

2.4 整体壁板压弯成形整体变形有限元仿真预测

实际生产中生产人员更为关注的是压弯结束后成形件的整体变形情况是否满足精度要求，而整体变形精度由压弯件的曲线形状保证[24]。增量压弯成形变形过程复杂，采用理论解析方法难以直接预测下一压弯过程的弯曲力学行为，进而获得增量压弯成形卸载前后的外形轮廓曲线。有限元仿真是分析金属塑性成形过程的有效手段。考虑到整体壁板压弯成形时压点之间相互影响以及筋板部分对压弯成形的影响，为获得准确的压弯成形整体变形曲线，建立整体壁板试件压弯成形整体变形三维有限元仿真预测模型。

采用有限元分析软件Abaqus，建立压弯成形限元模型。压头和支撑体的直径分别为10 mm和15 mm，支撑跨距为50 mm。假设试件材料为各向同性[25]并服从Mises屈服准则，压头和支撑体为刚体，试件是可变形体；按照图5和表1中单拉实验获得的材料参数赋予试件材料力学性能。试件网格划分采用C3D8R网格，压头和支撑体采用刚体离散单元R3D4，网格尺寸均为1 mm×1 mm；压头和壁板以及支撑体和壁板的接触面定义为面-面接触，其中压头和支撑体设为主面，为了计算更易于收敛，接触面之间设置有0.1 mm的间隙；实际压弯过程中，压头、支撑体与试件之间的摩擦为干摩擦，在有限元模拟时根据文献[26]，设置压头、支撑体和试件之间的摩擦系数为0.1；压弯过程中支撑体的自由度完全约束，压头通过参考点在Y向施加位移载荷。建立的有限元仿真模型如图9所示。为了保证收敛性和计算效率，采用Abaqus/Explicit对压弯成形过程进行分析；载荷施加结束后，通过更改约束条件并去除压头和支撑体建立回弹模型，将载荷施加结束后的仿真结果作为试件的初始状态，采用Abaqus/Standard对卸载回弹过程进行分析。

图9 有限元仿真模型Fig.9 Finite element simulation model

在CSS-44100电子万能实验机上对压弯成形有限元仿真预测模型进行实验验证。加载过程如图10(a)所示，左右压点位置的下压量为3 mm，中间压点位置的下压量为3.5 mm，压弯成形后的试件如图10(b)所示，通过便携式三维照相测量仪获取成形试件的外形轮廓数据。

图10 压弯成形实验Fig.10 Bending forming experiments

压弯过程中弯曲力的准确性直接影响到有限元模拟的可靠性。因此通过实验获得的力-位移关系曲线验证有限元模拟结果的有效性，同时对压弯件的几何形状也进行对比。采用应用最为广泛的三次B样条曲线对成形后试件的外形曲线进行拟合，将压弯过程中力-位移曲线和压弯成形结束后获得的成形试件外形轮廓曲线与压弯实验结果进行对比，如图11所示。下压量分别为3 mm 和3.5 mm时，压弯过程中力-位移曲线实验值与有限元模拟值之间的最大偏差分别为8.84% 和7.6%；压弯结束后试件外形轮廓曲线实验值与有限元模拟值之间的最大偏差为13.46%，所建立有限元模型精度满足工程要求，可以用于压弯成形精度控制研究。

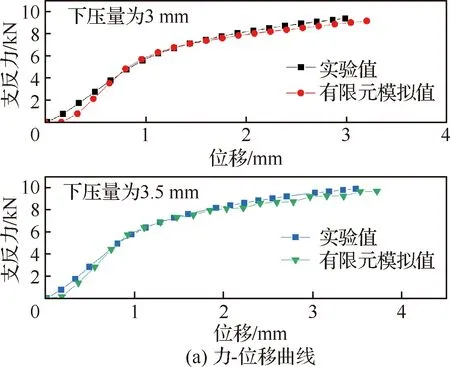
图11 有限元模拟与压弯实验对比Fig.11 Comparison between finite element simulation and bending experiment

3 结果分析

构造目标曲线为半径R=1 430 mm的圆弧[27]，如图12(a)所示，压点位置如图12(b)所示，根据几何关系，3个压点处的初始下压量为0.9 mm。

图12 目标形状Fig.12 Target shape

压弯成形局部变形下压量预测及局部-整体变形精度计算均在MATLAB中进行。根据式(10)，通过数值迭代法计算获得目标成形曲线所需的下压量为1.025 mm，将下压量作为压弯成形的初始边界条件，按照图3所提方法获得目标成形曲线的迭代过程如图13所示。由图13(a)，补偿前压弯曲线与目标曲线最大形状偏差为1.363 mm，整体变形误差为0.298 mm。取补偿因子为0.7，计算第1次下压补偿量为0.21 mm，补偿后压弯曲线与目标曲线之间的形状最大偏差减小到0.021 mm，整体变形误差为0.004 7 mm，如图13(b) 所示。经过一次迭代成形后，压弯成形形状整体变形精度提高了98.4%。

图13 基于本文方法的成形曲线迭代过程Fig.13 Iterative process of contour curves based on the proposed method

以图12中目标成形曲线几何下压量作为初始值采用试错法进行整体壁板压弯成形形状控制，曲线迭代补偿过程如图14所示。图14(a)为补偿前压弯成形后曲线，补偿前压弯曲线与目标曲线最大形状偏差为2.133 mm，整体变形误差为0.466 mm。选择压点位置作为控制点，计算控制点处与目标曲线的偏差，取补偿因子为0.8，计算得到第1次迭代成形下压补偿量为0.26 mm，由图14(b)，经过第1次补偿后，压弯曲线与目标曲线之间的形状最大偏差减小到0.56 mm，整体变形误差为0.122 mm。取补偿因子为0.8，计算第2次迭代成形下压补偿量为0.1 mm，由图14(c)，压弯曲线与目标曲线之间的形状最大偏差减小到0.139 mm，整体变形误差为0.029 mm。经过两次迭代成形后，压弯成形形状整体变形精度提高了93.5%。本文所提方法与试错法获得的压弯成形整体变形误差随着迭代的变化过程对比如图15所示。

图14 基于试错法的成形曲线迭代过程Fig.14 Iterative process of contour curves based on trial and error method

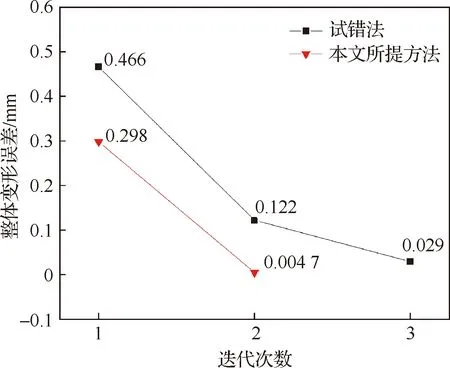
图15 整体变形误差随迭代的变化Fig.15 Evolution of global deformation error with iterations

4 结 论

1) 采用理论解析和有限元模拟相结合的方法，对整体壁板压弯成形局部-整体变形进行预测；利用迭代补偿机制与逐步逼近思想，提出了整体壁板压弯成形的形状控制方法。

2) 以设计的机翼整体壁板实验样件为例，对所提方法进行了验证。经过一次迭代后，变形件整体变形误差由0.298 mm降低至0.004 7 mm，压弯成形形状整体变形精度提高了98.4%。

3) 通过与传统的试错法进行对比，本文所提方法能够以更高的精度、更快的收敛速度有效控制压弯件的成形形状。