基于后缘襟翼偏转的大型客机变弯度技术减阻收益

何萌，杨体浩，白俊强，杨一雄

1. 西北工业大学 航空学院，西安 710072 2. 西北工业大学 无人系统技术研究院，西安 710072

随着人们对绿色生活环境关注度的增加以及燃油价格的不断上涨，未来民航客机的经济性和环保性越来越重要[1]。机翼后缘变弯度的设计增强了机翼适应各种飞行条件的能力,使工程师能在各工况下设计机翼不同的后缘偏角以改善其气动性能,而不是一系列飞行条件下的气动性能之间的折衷，是一种有效的减小燃油消耗的技术。

Boeing和NASA共同开展了“可变弯度后缘襟翼”(Variable Camber Continuous Trailing Edge Flap，VCCTEF)项目研究[2-3]，探索了变弯度技术用于未来质量更轻、机翼柔性更大的飞行器的性能优势，比如提高巡航效率、扩宽抖振边界、增加机动性等。Boeing757的原型机GTM(Generic Transport Model)构型上使用此项技术，有效减小了其巡航阻力[4-5]。Boeing787也采用了机翼后缘变弯度设计，所减少的巡航阻力相当于节省340～450 kg(750～1 000 lb)的重量[6]。

变弯度的结构设计[7-9]目前具有较高的技术储备，比如FlexSys FlexFoil装置[10-11]改变襟翼偏角时，控制表面仍能呈现出平滑和连续的过度。国内外学者对机翼后缘变弯度技术在气动设计中的收益也已经开展了广泛的研究。Molinari等[12-13]和Lee等[14]使用低精度气动模型研究了后缘连续变弯的优点；Lyu和Martins[15-16]使用高精度的伴随求解器对CRM机翼后缘连续变弯度技术的收益进行研究，对407个可能的飞行状态进行后缘变弯度的优化，生成一个优化构型的数据库，分析了后缘变弯度技术对燃油消耗的减小量，但是没有考虑到配平阻力对减阻收益的影响。Burdette等[17-18]使用气动结构求解器对后缘变弯度的收益进行了研究，结果表明，可变弯的机翼有1.02%的燃油收益，考虑结构变形的影响，燃油可减小1.72%。梁煜[19]和陈钱[20]等以翼型为例，研究了翼型后缘变弯度对气动性能与压力分布的影响。郭同彪等[21-22]研究了后缘连续变弯度对跨声速翼型气动特性的影响，以及针对民用客机机翼-机身-平尾构型开展了后缘连续变弯度机翼气动优化设计。

之前的工作主要针对二维翼型以及机翼全翼展连续变弯对气动特性的影响研究，全翼展连续变弯是机翼成型各控制剖面后缘均可变弯，设计变量较多，且对机翼变形材料要求较高，在规律研究上具有指导意义。但是针对大型客机，连续变弯技术的技术成熟度和可靠性有待进一步提高，目前尚无法在工程实际中得到应用。波音公司为787飞机测试和开发了一种后缘可变弯度(TEVC)系统，在巡航时通过操纵后缘内外襟翼以0.5°为增量进行偏转[6]。本文考虑了工程实际约束的影响，只对内外襟翼进行变弯偏转(具有两个设计变量)，对宽体客机进行了减阻收益评估。在考虑配平阻力的影响下探究了变弯度技术对阻力发散和抖振边界设计要求的拓展能力，以及变弯度技术在非设计点的减阻收益；内外襟翼偏角不同可能会使气动性能的改善效果更好，但会导致机翼后缘变弯机构更加复杂，因此对比了襟翼同偏和差偏在气动上的减阻收益；分析了在不同非设计点机翼后缘变弯度技术的压力分布变化规律、载荷分布变化规律，并进一步采用远场阻力分解方法探究了变弯度技术的减阻机理。

1 三维机翼后缘变弯度建模

变弯度时使用如图1 所示的襟翼平面形状，具有两个设计变量，分别为内襟翼偏角和外襟翼偏角。采用定轴偏转的方式偏转襟翼，偏转前后的效果对比如图2 所示，可以看到，变弯度后的翼面依然保持着连续、光滑的特征。同时由于机构的行程和精度限制，要求襟翼以0.5°的卡位运行，且最大偏角不超过2°，规定襟翼下偏为正，上偏为负。平尾也作为一个额外的自由度参与考虑，即通过平尾安定面的偏转来配平俯仰力矩,使变弯度构型的俯仰力矩与基础构型一致。

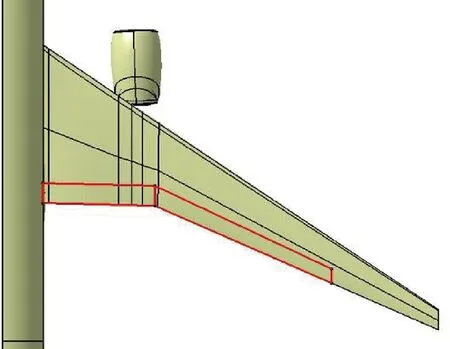
图1 襟翼平面形状Fig.1 Flap plane shape

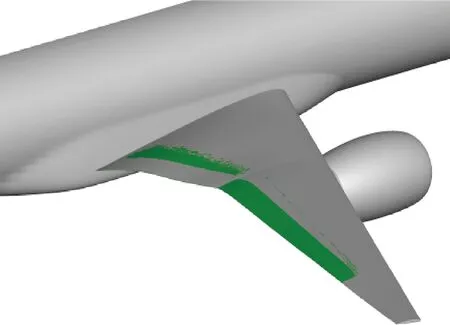
图2 变弯度偏转效果Fig.2 Variable camber deflection effect

由于挂架只对局部的流场产生影响，对整体气动特性影响不大[23-24]，且为了减小网格量和减小流场的复杂性，建模时没有考虑挂架的影响[25]。

2 数值求解方法

本文使用雷诺-平均Navier-Stokes (RANS)方程求解器进行定常求解。全湍流计算，使用的湍流模型为剪切应力输运(SST)湍流模型。选取CRM翼身组合体构型[26]对求解器精度进行校验，网格量为1 725万，计算状态为:马赫数Ma=0.85, 雷诺数Re=5×106, 升力系数CL=0.519。

4个控制剖面的压力系数Cp分布计算结果与试验数据的对比如图3 所示，求解器计算得到的压力分布形态与试验值吻合良好，尤其是下表面贴合较好。对比结果表明，本文采用的求解器具有可满足工程应用需求的计算精度和可靠性。宽体构型计算时采用多块结构网格，网格拓扑如图4 所示。

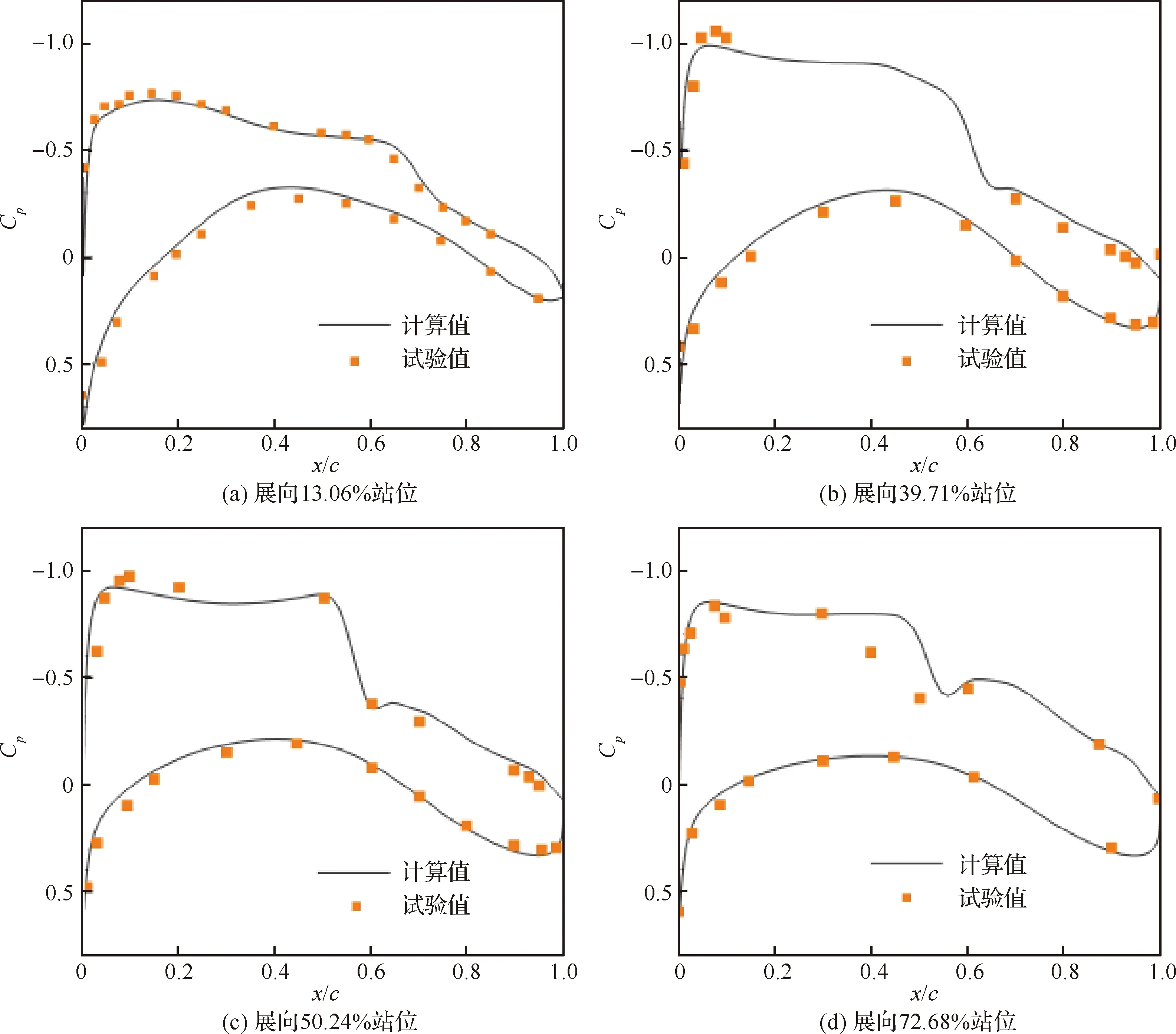
图3 CRM构型计算结果与试验数据对比Fig.3 Comparison of CRM configuration calculation results with experimental data

图4 计算网格拓扑Fig.4 Grid topology

为了明确网格量对计算结果的影响，本文计算了2 000万、3 000万和4 300万网格量下阻力系数的数值，计算结果如表1 所示。使用2 000万网格计算时，相较于3 000万的网格量，计算出来的阻力值增加7.5 counts(1 count=0.000 1)，使用4 300万的网格相较于3 000万的网格，阻力值只增加了约2 counts。从工程应用研究角度，可认为3 000万网格与4 300万网格具有相当的计算精度水平。考虑到本文计算量大，为了兼顾计算时间和计算精度，最终采用3 000万的网格量用于变弯度技术减阻收益的评估。

表1 基础构型不同网格量计算结果

3 基础构型气动性能

表2给出了未考虑襟翼变弯的基础构型气动特性，设计马赫数Ma=0.85，设计升力系数CL=0.48，雷诺数Re=4.7×107。巡航设计点力矩基本配平，巡航攻角为2.48°，阻力系数为230.98 counts，升阻比为20.78。马赫数0.87与马赫数0.85的阻力差量为17.53 counts，阻力发散特性较好。图5 为马赫数0.85机翼表面压力分布及流线图。

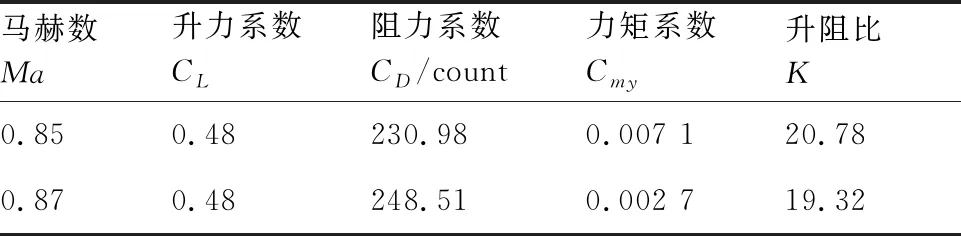
表2 基础构型气动性能Table 2 Aerodynamic performance of original configuration

图5 马赫数0.85机翼表面压力系数分布及流线图Fig.5 Pressure coefficient distribution and surface streamline of wing (Ma =0.85)

4 采用变弯度技术的状态选取

变弯度技术能够在巡航过程中通过改变后缘偏角，在非设计点状态下获得减阻收益，从而降低整个巡航段的平均阻力。因此，本文选取的变弯度技术减阻收益评估状态包括以下3类：

1) 随着飞行过程中燃油不断消耗，飞机的升力系数也会随时间发生变化[17,27]。故选取了升力系数变化10%和20%的非设计点，即小升力系数点(CL=0.432和CL=0.384)和大升力系数点(CL=0.528和CL=0.576)。在此基础上，进一步分析整个升力系数变化范围内的减阻规律。

2) 受航空管制以及变高度巡航策略等因素的影响，民用客机难以在整个巡航阶段内都以一个固定的设计马赫数进行巡航，其巡航马赫数往往会在设计马赫数附近小幅变化[17]。故选取了马赫数偏小点(Ma=0.83，CL=0.48)和阻力发散点(Ma=0.87，CL=0.48)进行变弯度技术的减阻收益研究。

3) 研究变弯度技术对升力系数增加所引起的高速抖振特性的影响。对于大型民用客机，设计规范要求其具有1.3 g的抖振裕量，故重点研究了变弯度技术对抖振点(Ma=0.85，CL=0.624)气动特性的改善作用。

最终，选取的计算状态的分布如图6 所示。

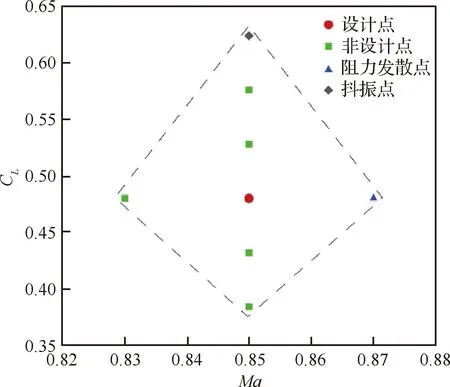
图6 变弯度设计的计算状态分布Fig.6 Calculation condition distribution of variable camber design

5 变升力系数状态后缘变弯技术减阻收益

5.1 小升力系数下的减阻收益

对内外襟翼的可能偏角进行遍历计算，表3给出了CL=0.384状态下基础构型、不考虑力矩配平阻力的最佳襟翼偏角构型、考虑配平阻力的最佳襟翼同偏构型和最佳襟翼差动偏转构型结果。襟翼同偏表示内、外襟翼的偏角一致，差动偏转表示内、外襟翼的偏角不一致。

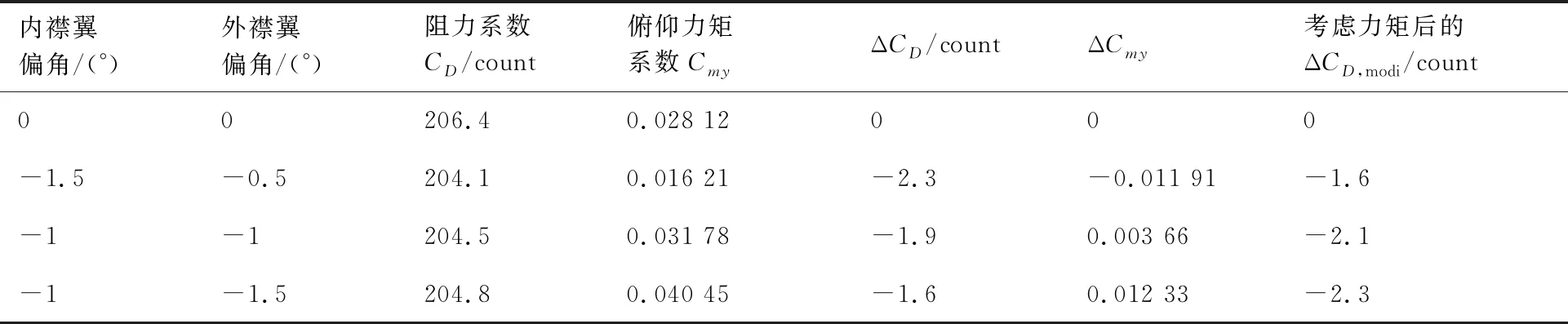
表3 基础构型与最优襟翼偏角构型气动力系数(CL=0.384)Table 3 Aerodynamic coefficients of original configuration and optimal flap declination configuration (CL=0.384)

图7给出了CL=0.384时的计算结果，Inner表示内襟翼偏角，Outer表示外襟翼偏角，可以看到小升力系数时襟翼上偏有助于阻力减小，内襟翼上偏，外襟翼下偏，造成低头力矩增加，而襟翼同偏对力矩系数的影响不大。不考虑力矩配平阻力的最优襟翼偏角为内襟翼-1.5°，外襟翼-0.5°，减阻2.3 counts；考虑配平阻力后仅减阻1.6 counts；考虑配平阻力下最佳同偏襟翼偏角为-1°，减阻2.1 counts，最佳差动偏转襟翼偏角为内襟翼-1°，外襟翼-1.5°，减阻2.3 counts。

表4和图8给出了CL=0.432的计算结果，不考虑力矩配平阻力的最佳襟翼偏角为内襟翼-1.0°，外襟翼-0.5°，减阻1.4 counts;考虑配平阻力后仅减阻1.2 counts；考虑配平阻力下最佳襟翼偏角为内襟翼-0.5°，外襟翼-0.5°，减阻1.4 counts。可见，是否考虑力矩配平对最佳襟翼偏角和减阻量有较大影响，在进行变弯度减阻收益研究时有必要考虑配平阻力的影响。

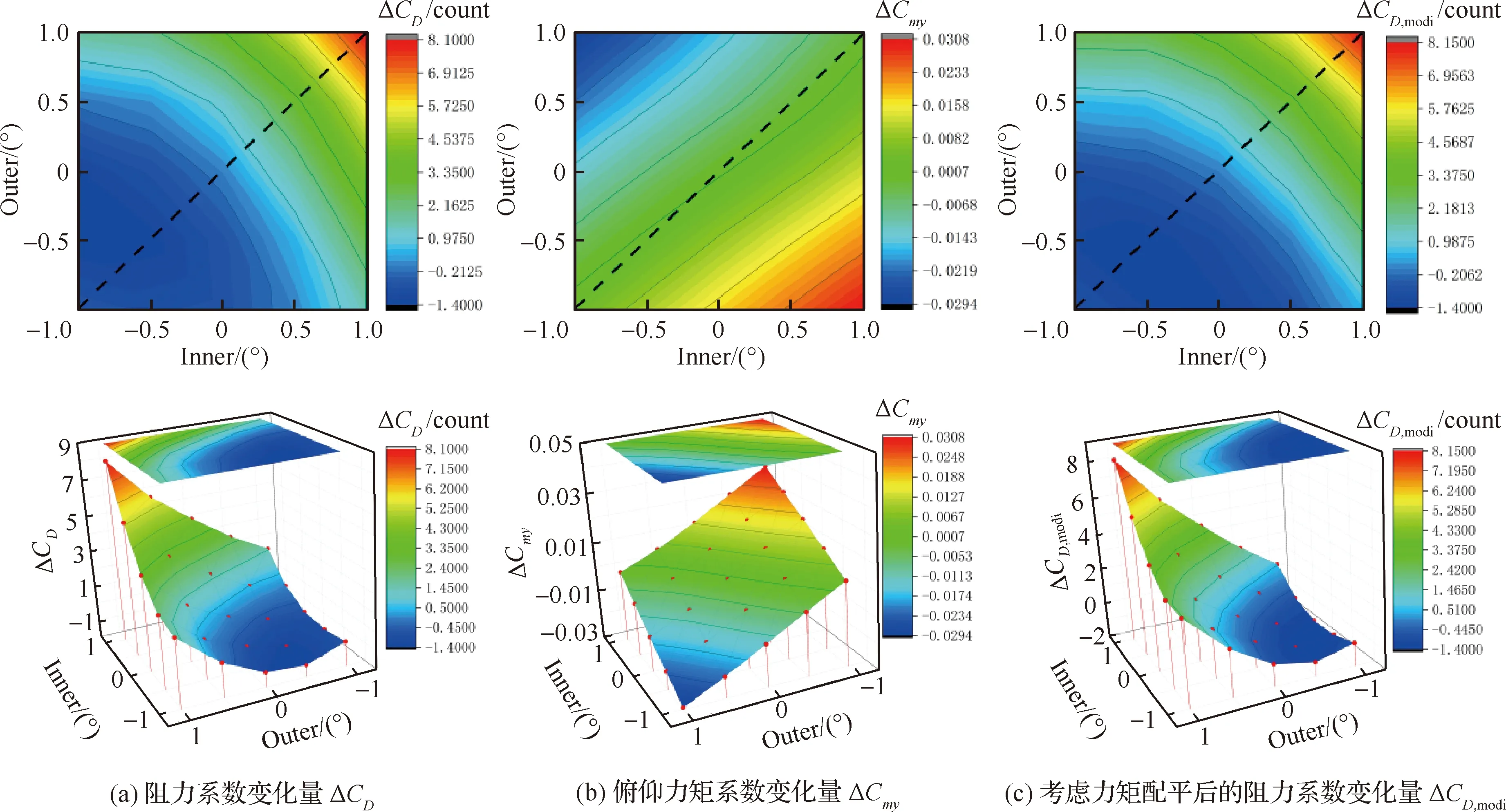
图8 不同内外襟翼偏角下的气动阻力以及俯仰力矩系数变化云图(CL=0.432)Fig.8 Contour of aerodynamic drag and pitching moment coefficient at different inner and outer flaps (CL=0.432)

表4 基础构型与最优襟翼偏角构型气动力系数(CL=0.432)Table 4 Aerodynamic coefficients of original configuration and optimal flap declination configuration (CL=0.432)

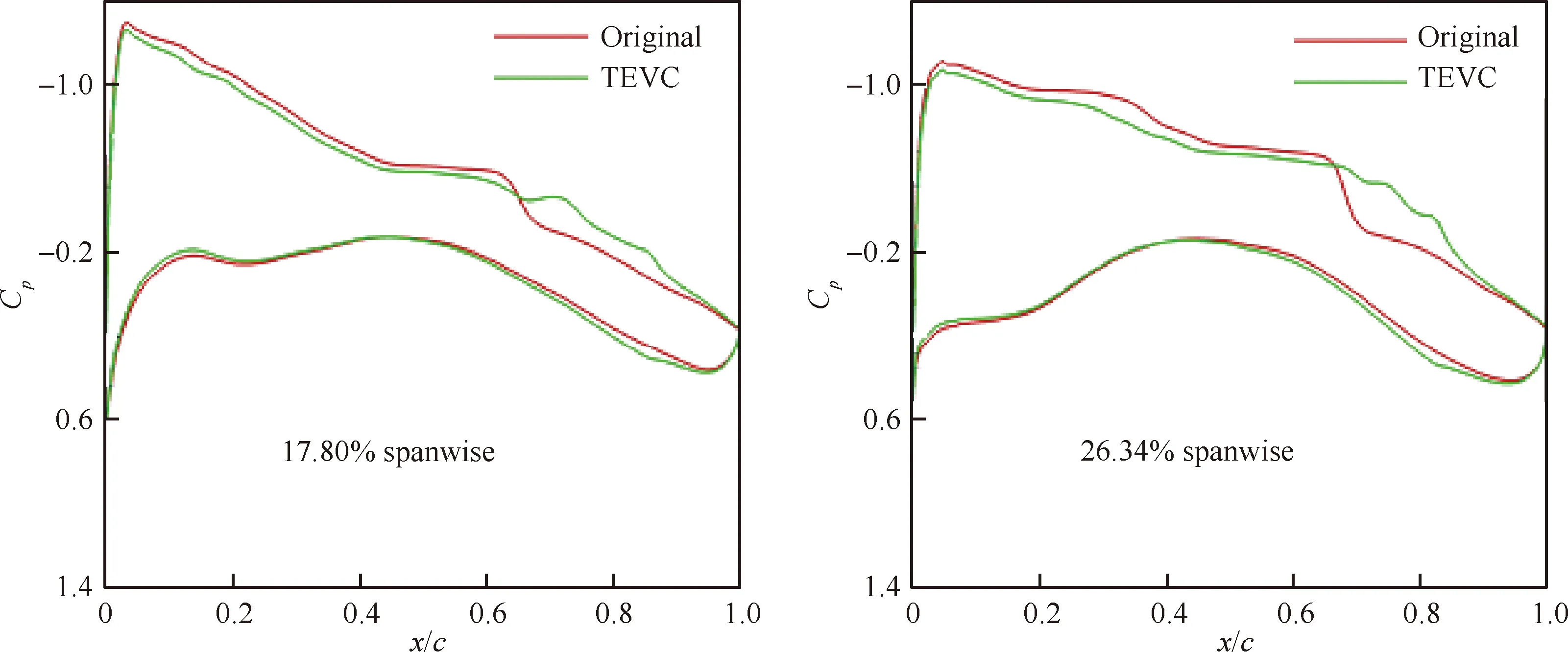
图9、图10 给出了变弯前后机翼上激波强度对比、环量分布对比及剖面压力系数Cp对比，Original 表示基础构型，TEVC表示变弯构型(襟翼同偏最优结果)。对于小升力系数的计算工况，内外襟翼均上偏使得机翼后缘卸载，巡航攻角增大，引起激波位置后移，载荷前移。机翼载荷前移导致抬头力矩增加。同时机翼中后缘部分载荷减小，使压力恢复平缓，激波强度减小。通过机翼展向环量分布对比可以看出，机翼襟翼的同时上偏使载荷外移，更加贴近椭圆形环量分布。

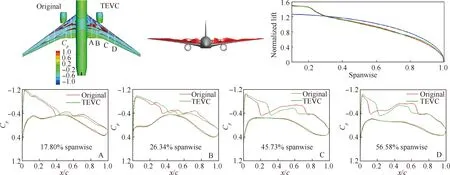
图9 变弯前后对比(内襟翼-1°，外襟翼-1°，CL=0.384)Fig.9 Comparison of initial and flap deflection configurations (inner flap -1°, outer flap -1°, CL=0.384)

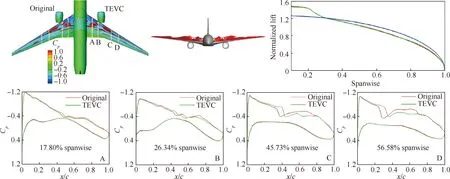
图10 变弯前后对比(内襟翼-0.5°，外襟翼-0.5°，CL=0.432)Fig.10 Comparison of initial and flap deflection configurations (Inner flap -0.5°, Outer flap -0.5°, CL=0.432)

5.2 大升力系数下减阻收益

表5和图11 给出了CL=0.528的计算结果，从图11 可以看出，大升力系数下，襟翼下偏有助于阻力减小，襟翼偏角变化对力矩系数的影响与小升力系数时基本一致。不考虑力矩配平阻力的最佳襟翼偏角为内襟翼0.5°，外襟翼1.0°，减阻5.5 counts;考虑配平阻力后仅减阻4.2 counts；考虑配平阻力的最佳同偏襟翼偏角为1°，减阻5.0 counts，最佳差动偏转襟翼偏角为内襟翼1.5°，外襟翼0.5°，减阻5.7 counts。

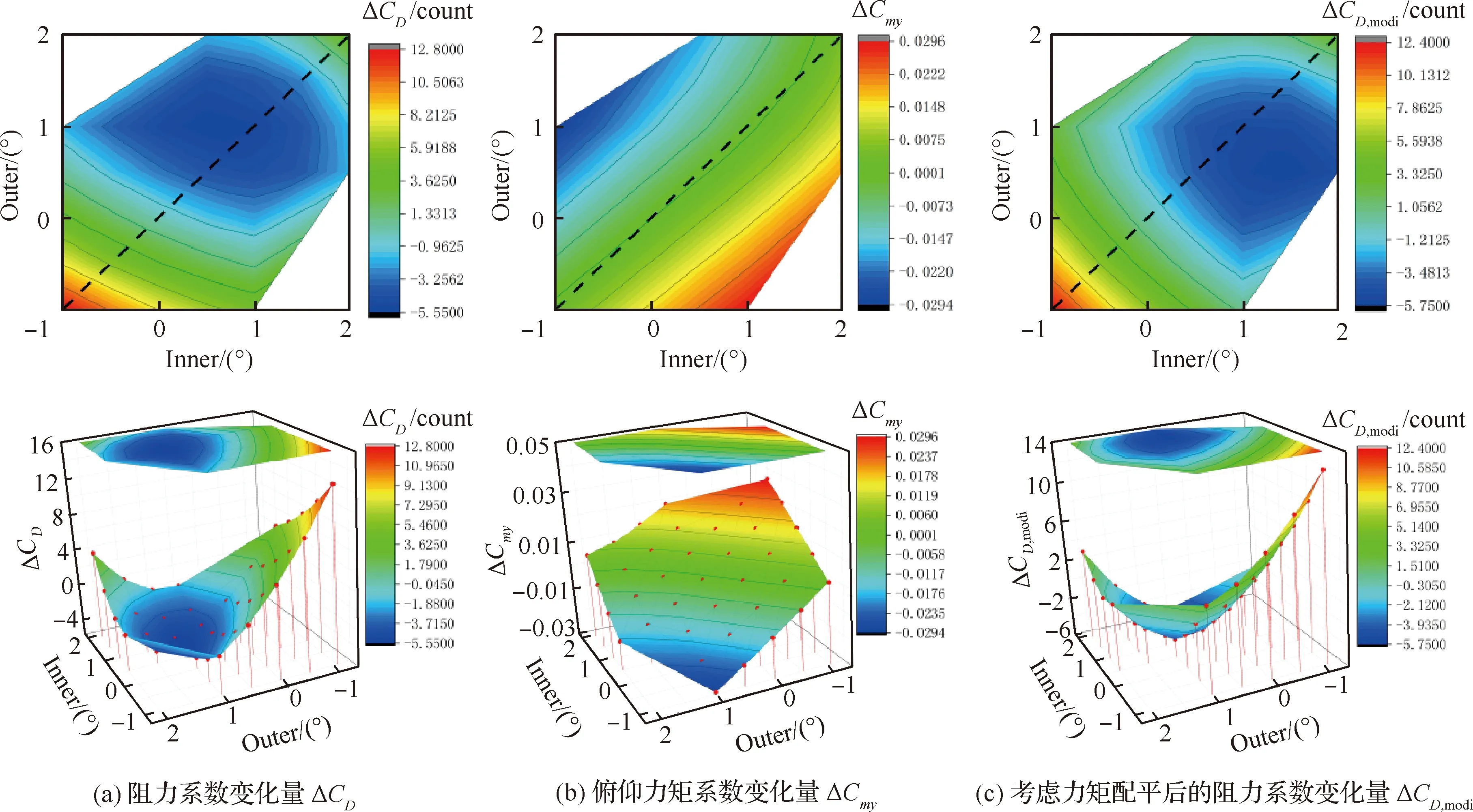
图11 不同内外襟翼偏角下的气动阻力以及俯仰力矩系数变化云图(CL=0.528)Fig.11 Contour of aerodynamic drag and pitching moment coefficient at different inner and outer flaps (CL=0.528)

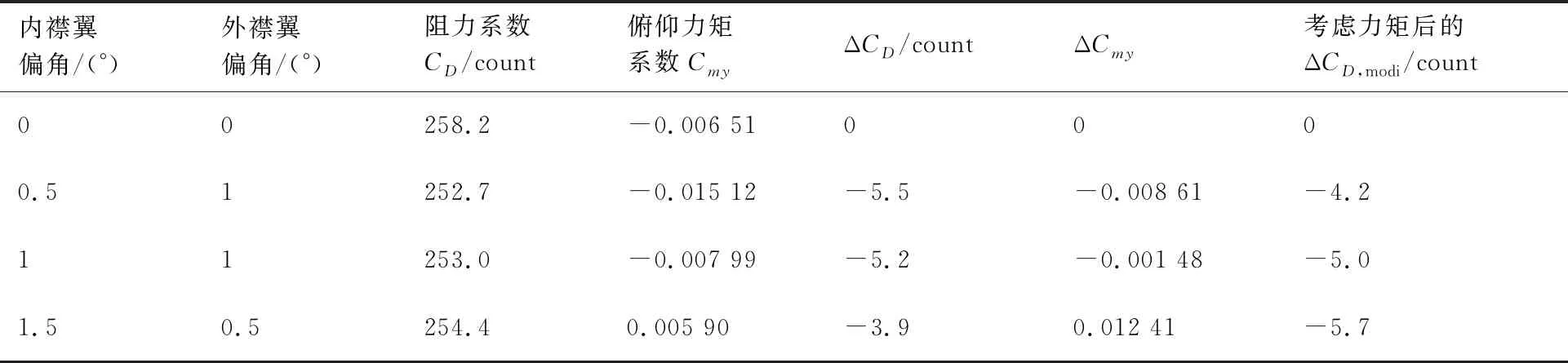
表5 基础构型与最优襟翼偏角构型气动力系数(CL=0.528)Table 5 Aerodynamic coefficients of original configuration and optimal flap declination configuration (CL=0.528)

表6和图12 给出了CL=0.576的计算结果，不考虑力矩配平阻力的最佳襟翼偏角为内襟翼1.0°，外襟翼1.5°，减阻14.0 counts；考虑配平阻力后仅减阻12.2 counts；考虑配平阻力的最佳同偏襟翼偏角为1.5°，减阻12.9 counts，最佳差动偏转襟翼偏角为内襟翼2.0°，外襟翼1.0°，减阻13.5 counts。大升力系数下，变弯度技术具有较为明显的气动性能的改善。配平阻力依然对结果有较大影响，在进行变弯度减阻收益研究时有必要考虑配平阻力的影响。

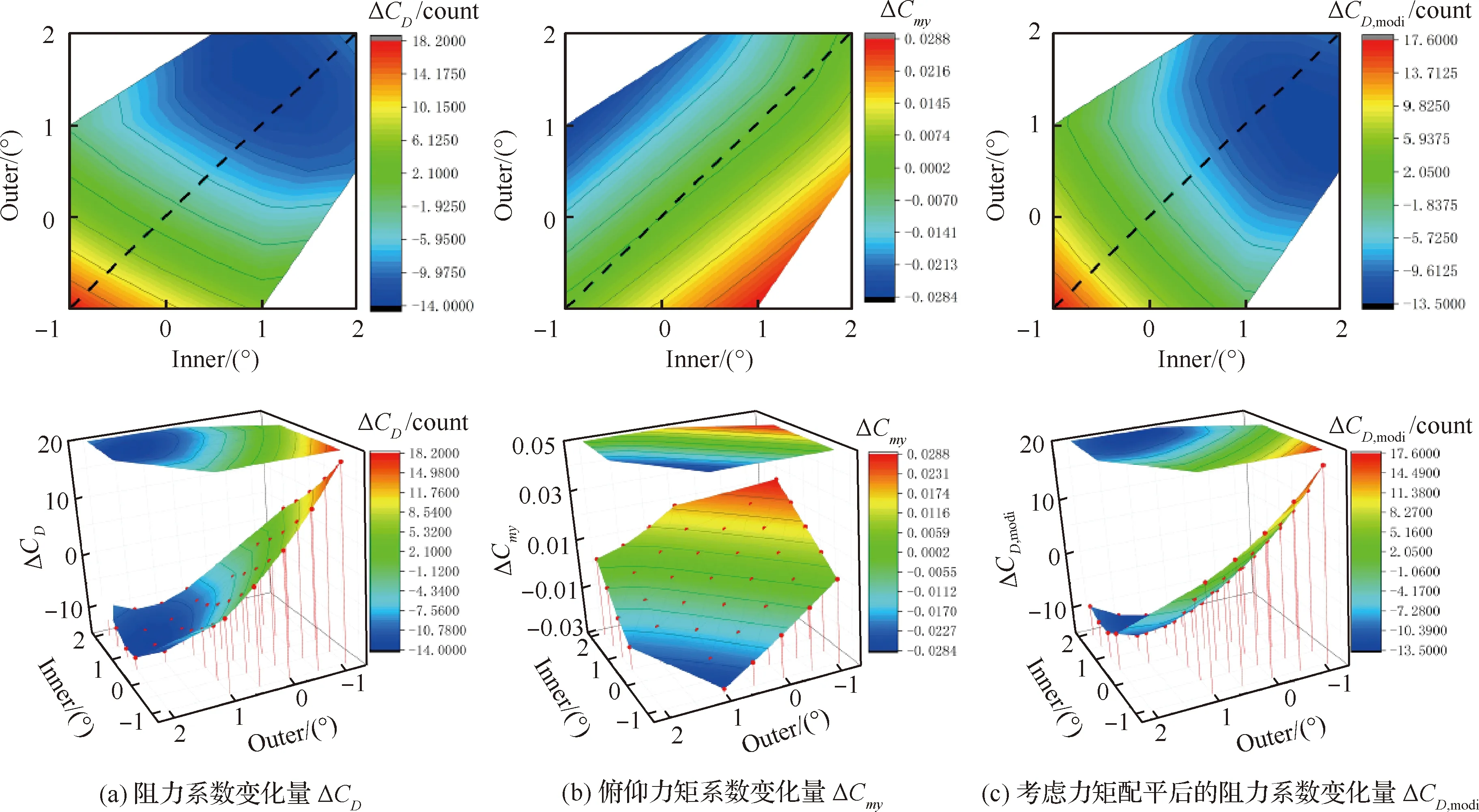
图12 不同内外襟翼偏角下的气动阻力以及俯仰力矩系数变化云图(CL=0.576)Fig.12 Contour of aerodynamic drag and pitching moment coefficient at different inner and outer flaps (CL=0.576)

表6 基础构型与最优襟翼偏角构型气动力系数(CL=0.576)Table 6 Aerodynamic coefficients of original configuration and optimal flap declination configuration (CL=0.576)

图13和图14 给出了变弯前后机翼上激波强度对比、环量分布对比及剖面压力系数Cp对比。大升力系数下，内外襟翼均下偏使得机翼后缘加载，上翼面的压力分布会变得饱满，压力恢复平缓，激波强度降低，波阻减小。通过机翼展向环量分布对比可以看出，机翼襟翼的同时下偏使载荷内移，环量分布更加偏离椭圆形环量分布。

6 变马赫数状态减阻收益

6.1 马赫数偏小(Ma=0.83)时的减阻收益

从表7 和图15可看出在不考虑力矩配平阻力的影响下，内襟翼偏转-1°，外襟翼偏转0.5°，减阻0.5 counts，但此偏转条件下，低头力矩增加，考虑配平阻力后，阻力增加0.5 counts。

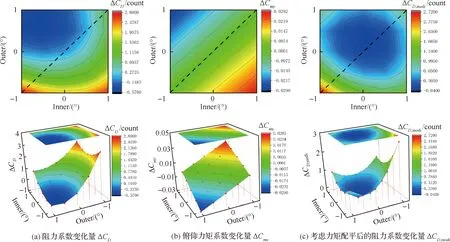
图15 不同内外襟翼偏角下的气动阻力以及俯仰力矩系数变化云图(Ma=0.83)Fig.15 Contour of aerodynamic drag and pitching moment coefficient at different inner and outer flaps (Ma=0.83)

表7 基础构型与最优襟翼偏角构型气动力系数(Ma=0.83)Table 7 Aerodynamic coefficients of original configuration and optimal flap declination configuration (Ma=0.83)

对于马赫数偏小的非设计点，首先由于激波位置在变弯区域之前且距离太远，变弯控制的效果较弱,没有较为明显的减阻效果。其次最优偏角为内襟翼上偏，外襟翼下偏，导致机翼载荷外移，低头力矩增加，造成配平阻力增加。因此考虑力矩配平的影响之后，变弯度技术对马赫数偏小的非设计点没有带来气动特性的改善。

6.2 阻力发散点(Ma=0.87)的减阻收益

从表8 和图16可看出在不考虑力矩配平阻力的影响下，内襟翼偏转-1°，外襟翼偏转0.5°，减阻1.4 counts，但此偏转条件下，低头力矩增加，考虑配平阻力后，阻力增加2.4 counts。

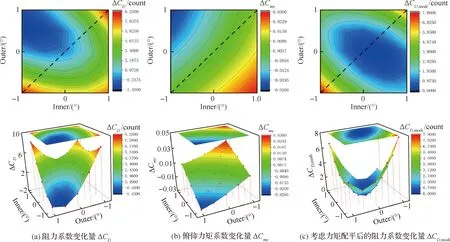
图16 不同内外襟翼偏角下的气动阻力以及俯仰力矩系数变化云图(Ma=0.87)Fig.16 Contour of aerodynamic drag and pitching moment coefficient at different inner and outer flaps (Ma=0.87)

对于阻力发散点，首先由于激波位置靠后，以至于在变弯度过渡区之后，变弯控制的效果也很弱。其次考虑力矩的影响之后，配平阻力的增加使变弯度技术对阻力发散点也没有带来气动特性的改善。

在不同的马赫数下，不论是马赫数增大还是减小，内襟翼上偏、外襟翼下偏导致机翼载荷外移，低头力矩增加，考虑力矩系数后，变弯度的减阻收益均为0。

7 变弯度技术对抖振特性的改善作用

表9和图17 给出了CL=0.624抖振点的计算结果，考虑力矩配平阻力时，最佳同偏襟翼偏角为1.5°，减阻18.8 counts，最佳差动偏转襟翼偏角为内襟翼2.0°，外襟翼1.0°，减阻21.2 counts。

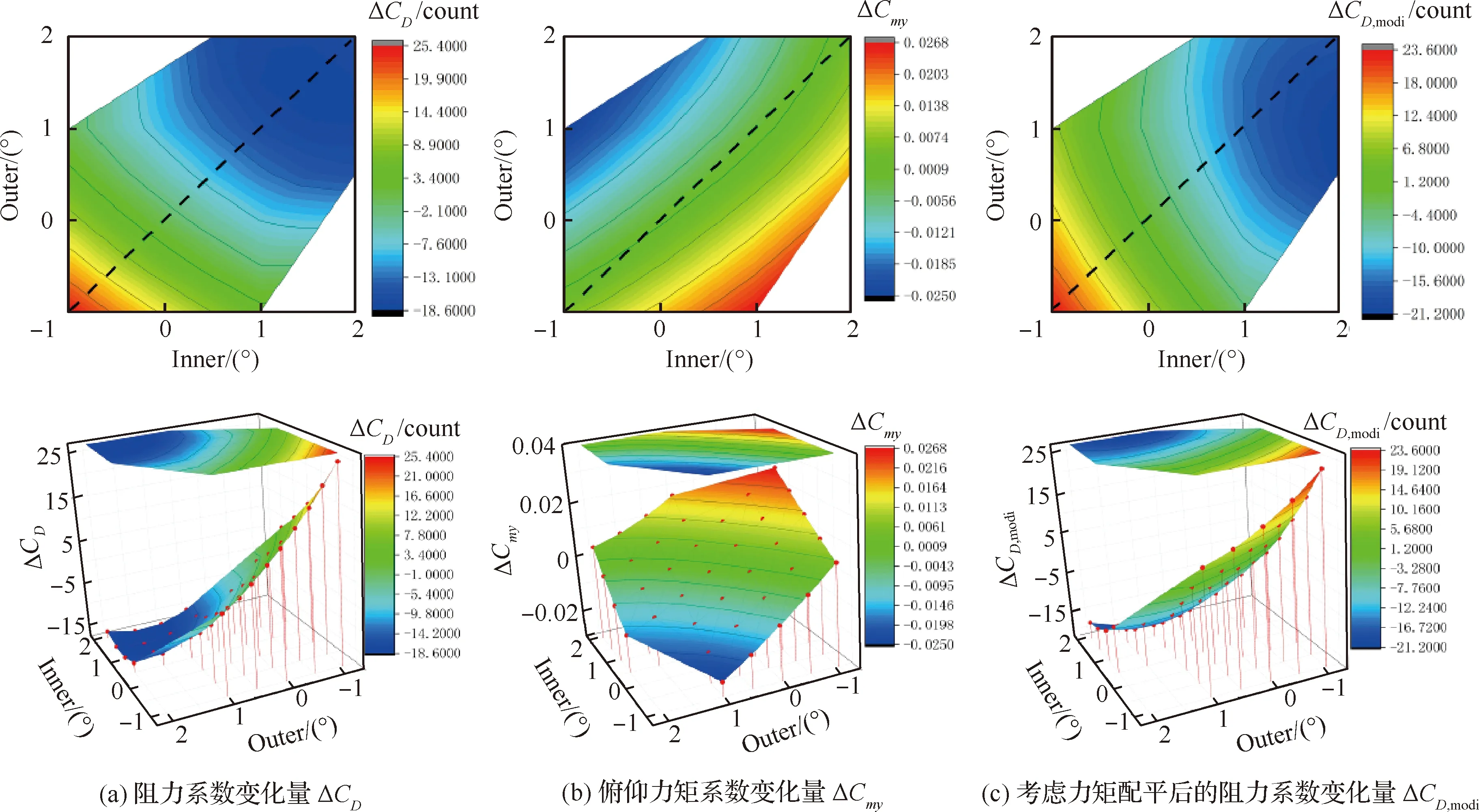
图17 不同内外襟翼偏角下的气动阻力以及俯仰力矩系数变化云图(CL=0.624)Fig.17 Contour of aerodynamic drag and pitching moment coefficient at different inner and outer flaps (CL=0.624)

表9 基础构型与最优襟翼偏角构型气动力系数(CL=0.624)Table 9 Aerodynamic coefficients of original configuration and optimal flap declination configuration (CL=0.624)

图18给出了抖振点襟翼同偏变弯前后机翼剖面压力系数Cp对比。内外襟翼下偏，机翼后缘载荷增加。内翼段通过襟翼下偏，压力恢复平缓，呈无激波形态，中外翼段通过外襟翼下偏，激波位置后移，激波强度减小。

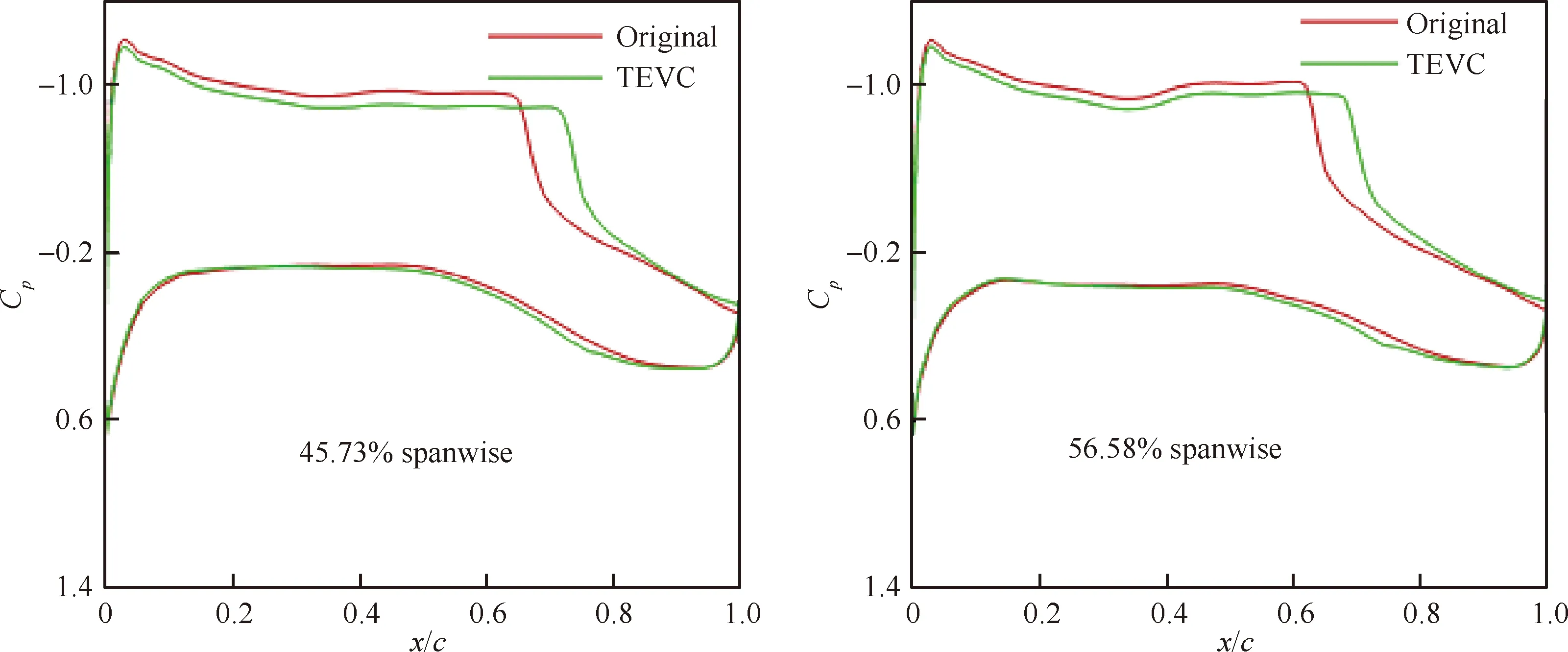
图18 襟翼同偏变弯前后机翼剖面压力系数对比(内襟翼1.5°，外襟翼1.5°，CL=0.624)Fig.18 Comparison of wing section pressure coefficient of original and flap deflection configurations (Inner flap 1.5°, Outer flap 1.5°, CL=0.624)

抖振是激波附面层干扰引起分离流产生的非定常气动力引起的振动现象[28]。图19 为变弯前和变弯后的抖振特性对比，给出了一系列升力系数下的机翼上表面压力云图与极限流线。变弯前构型在CL=0.594和CL=0.604下的分离区大小分别接近于变弯后构型在CL=0.624和CL=0.634下的分离区大小，结果表明变弯度可改善抖振特性。变弯度通过调整载荷分布，明显降低中外翼激波强度，减缓了激波诱导分离的趋势。

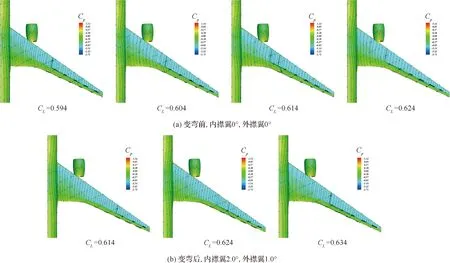
图19 变弯前和变弯后抖振特性对比Fig.19 Comparison of buffeting characteristics before and after flap deflection

8 变弯度技术非设计点减阻机理分析

图20给出了不同升力系数下变弯度的减阻情况(考虑力矩系数配平后),其中蓝线和绿线分别给出了同偏与差动偏转下的结果。可以看到，偏离设计点升力系数越远，变弯度获得的减阻收益越大，且大升力系数时的收益要大于小升力系数时的收益。对比同偏和差动偏转，两者减阻量随升力系数变化的变化趋势基本一致，差动偏转的收益略高于同偏的收益。

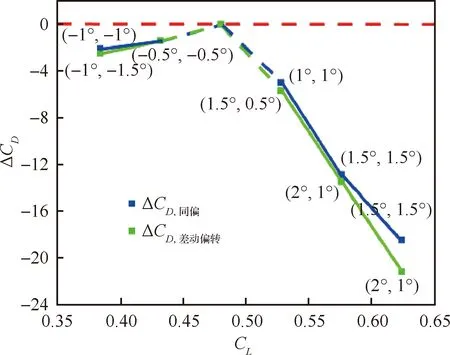
图20 不同升力系数下变弯度的减阻量(考虑力矩系数配平后)Fig.20 Drag reduction of variable camber under different lift coefficients (considering trimming moment coefficient)

进一步采用远场阻力分解方法[29-30]探究了变弯度技术的减阻来源，远场阻力分解方法是基于线性动量定理关系进行阻力计算，将阻力按照产生的机制分为黏性阻力、激波阻力、诱导阻力和伪阻力。

图21给出了不同升力系数下变弯前后激波阻力值对比，小升力系数状态下波阻减小量不足1 count。大升力系数状态下，波阻有明显的减小。波阻的减小主要是因为后缘襟翼变弯度技术会调整载荷分布，改变激波位置和强度。

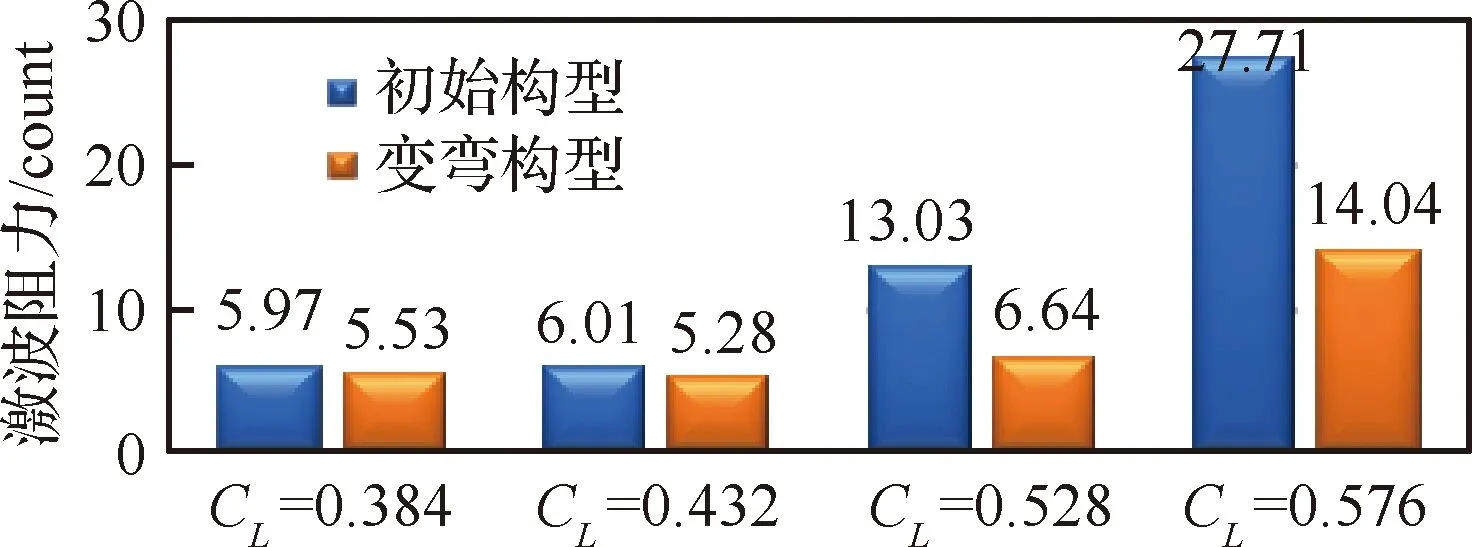
图21 变弯前后激波阻力对比Fig.21 Comparison of shock drag of original and flap deflection configurations

图22给出了不同升力系数下变弯前后诱导阻力值对比。在不同升力系数下，诱导阻力值没有明显改善。从之前的环量分布对比可以看出，在大升力系数时，载荷内移，更加偏离椭圆形环量分布，导致诱导阻力略微增加。

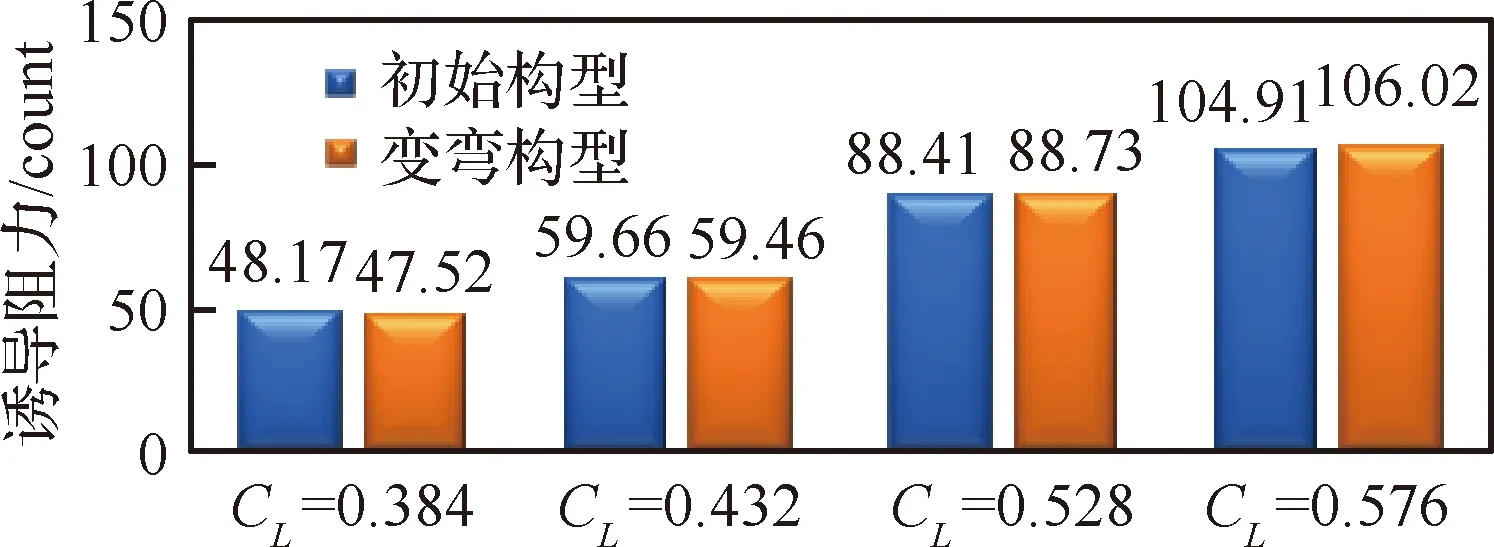
图22 变弯前后诱导阻力对比Fig.22 Comparison of induced drag of original and flap deflection configurations

9 结 论

1) 变弯度引起全机俯仰力矩变化带来的配平阻力，对变弯度减阻收益影响明显，考虑配平阻力损失是进行变弯度机翼设计的关键。

2) 在整个巡航升力系数范围内的非设计点，变弯度均能取得一定减阻收益，大巡航升力系数下减阻收益更大。不同巡航升力系数下变弯度减阻机理存在明显差异。小巡航升力系数下诱导阻力以及激波阻力都得到不同程度的减小。大巡航升力系数下以适当增大诱导阻力的方式，显著削弱激波阻力。

3) 变弯度通过将机翼载荷内移，削弱激波强度，减小激波诱导的附面层分离，拓展抖振边界裕度。

4) 变弯度无法改善阻力发散点和阻力蠕增特性。

5) 对比差动偏转和同偏，两者的减阻收益随升力系数的变化趋势一致，但在某些情况下，差动偏转减阻收益更明显。