数学让环形公交更畅通

王 莉

1 问题提出

泰安因五岳之首泰山闻名于世，近几年每年接待游客约5000 万人次，为满足游客需求和方便居民出行，泰安市公交公司开辟了K39 路环形公交路线。该路线连接着泰安市中心与东部新区，由泰山火车站出发，途径岱庙、天外村、红门、方特欢乐世界等旅游景点，以及泰安一中、山东服装职业学院、泰山职业技术学院三所学校，共计43 站。

存在问题：由于路线较长，站点较多，市区交通阻塞，等车时间时长时短，到站速度也是时快时慢，高峰时段车辆超载率高，乘客舒适度较差，反映强烈。

K39 是单车场环形运行，是不是调度上存在不合理因素？如何既能保证公交公司的经济利益，又能增加乘客的满意度呢？

2 问题分析

本问题要求设计一个环形公交车调度表，要同时考虑到完善城市交通环境、改进乘客出行状况、提高公交公司的经济和社会效益等诸多因素。如果仅考虑提高公交公司的经济效益，则只要提高公交车的满载率，如果仅考虑方便乘客出行，只要增加车辆的次数。显然这两种方案是对立的。所以需要在这几个因素中找出一个合理的匹配关系，使得双方的满意度达到最高。

3 问题调查

首先要对K39 路车客流情况进行调查，收集数据。基础数据有：线路总长：42×500 ≈21000 米，对 环 形 路 线，运 行 时 间 即 周 转 时 间：21000÷333 ≈64 分钟（时速按20KM/H），首末站停车时间：平峰期间首末站平均停站时间t=0.21tn(10 ≤tn≤100)min。则有：t=0.21×64 ≈14min。调查方法采用票据法和随车调查相结合。调查情况见附件。

4 提出假设

（1）交通情况、路面状况良好，无交通堵塞和车辆损坏等意外情况。

（2）全程为单一票价。

（3）线路上的公交车为同一型号,核定载客量为50 人。

（4）单位时间内的上下客车人数服从均匀分布。

（5）始末车站乘客数不重复计算。

（6）为了便于叙述，本文把公交车运营时间6：00 ～18：00 分为12 个时间段，分别为1，2，...，12。

5 模型建立与解决

根据问题分析，环形运行方式为单车场的单车型运行问题的多目标优化模型。我们在设计调度表时，应该考虑此表带给公交公司和乘客两方的利益，即公交公司和乘客对应的日平均满意度mg 和mc，各时段的满意度mgj和mcj，我们对影响各自满意度的因素做分析。

1）各时段的最大客容量，建立模型如下。

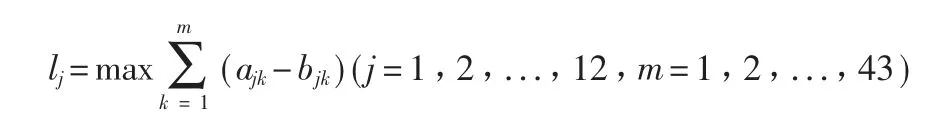
其中，ajk为第j 时间段第k 站的上车人数，bjk为第j时间段第k 站的下车人数。

运用模型和调查统计的上下乘客数，算出各个时间段内最大客容量。

2） 各个时段的发车次：由于公交车每辆标准载客50 人，车辆满载率在60%～120%之间，当zj 接近60 人，由模型。

可以计算出各时间段的发车次数cj，公交公司要满足最迟不超过15 分钟发一趟车，于是发车车次依次如下：7，9，8，6，6，7，6，7，5，5，9，8。

3）发车时间间隔：取每个时段60 除以车次数，得到该时段的平均发车时间间隔：sj=60/cj分钟，依次如下。

8.6，6.7，7.5，10，10，8.6，10，8.6，10，10，6.7，7.5。

为满足公交车载完每一段的乘客，综合1-3 的计算，得出了该工作日内的公交车应按如下方案调度。

4） 公交公司满意度：公交公司的满意度取决于公交车的平均载客量，公交车平均载客量越多，公交公司发车车次就少，对公交公司利益就大。在乘客源一定的情况下，影响mgj的主要因素是车上的乘客数即载客量zj，其中，一般情况下30 ≤zj≤60 。我们取各个时段的平均载客量zj的满意度

5）乘客满意度：对于乘客，影响mcj的主要因素是乘客的等车时间tj与车上的平均载客量zj。设mctj，mczj分别是各时段乘客因tj与zj的影响而产生的满意度，则mcj即 可 以 表 示 为：mcj=(mctj，mczj)A 其 中，A 是 关 于因素tj与zj的权重集。

考虑到，对于乘客，mctj，mczj对mcj的影响不是相等的，车辆的满载率达120%时，超载的20%由于缺少座位，注重舒适度的影响大于等待时间的影响；当满载率小于100%时，乘客因为有座，无需过分考虑舒适，更多的是考虑等车时间的影响。

表1 各个时间段内最大客容量

表2 该工作日内公交车的调度方案

由每时段的乘客满意度mcj，每时段的乘客最大客容量lj，一天最大客容量人数为可以算出乘客平均日满意度为各时段的满意度的加权平均值。

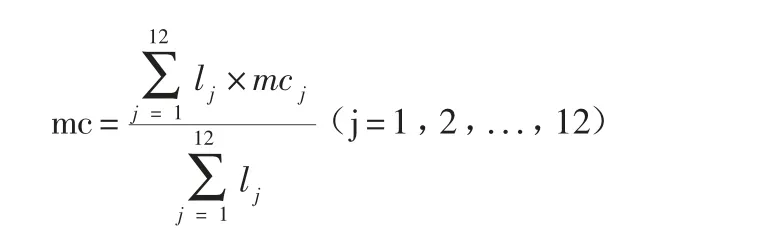
（6）合理调度情况分析。

对于公交公司，当满载60 人时公交公司最满意，人数越少，满意度越来越低。对于乘客，可知当等车时间不超过5 分钟，车辆满载率不超过100%时，乘客满意度为1，随着等待时间增加和车载率的上升，乘客满意度会逐渐下降。我们取当公交车平均载客人数分别为60 人，50 人，30 人时作分析。

（1） 当 zj→60 人， 则 乘 客 日 均 满 意 度 mg1=乘客的满意度mc1=0.7103。

（2）当zj→50 人时，公交公司满意度mg1=0.8326,乘客的满意度为mcj=0.9278。

（3） 当zj→30 人时 ，此时公交公司的利益达到最小，相应的乘客满意度会变大，公交公司满意度mg1=0.3907, 乘客满意度mc1=0.9813。

a、根据公交公司的满意度和乘客的满意度的对应关 系，(0.9811，7103)(0.8326，0.9278)(0.39207，0.9813)，可以利用二次拟合得出公交公司和乘客的函数f(mg1)。

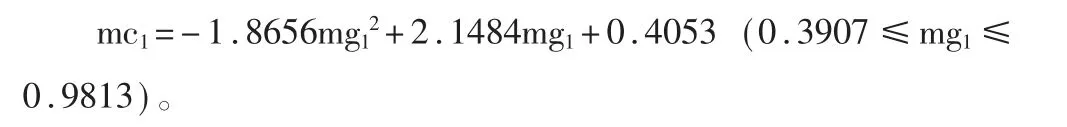
本题要求我们最大照顾到乘客和公交公司双方的利益，这就要求R=mc1+mg1能尽可能取大，即满足双方的利益最大化；同时我们也要使得双方满意度的差不能太大，即W=|mc1-mg1|尽可能取小。于是我们建立目标函数max=R-W=mc1+mg1-|mc1-mg1|，寻找出满足双方的满意度之和最大同时满足之差最小的最优满意度。联系函数分析，求的乘客和公交公司双方的匹配问题的最优满意度为mc1=0.8576，mg1=0.85676。

根据4-6 的计算，由最优满意度设计K39 路环形公交调度方案。

6 分析总结

该模型从实际问题出发，用常规方法做出的结果与实际情况较为统一。模型中涉及公交公司的满意度和乘客的满意度的拟合，为进一步合理设计新的调度方案提供依据。

存在不足：统计天数少，致使调查数据缺乏代表性。另外，乘客数量因天气、节假日等变动较大，如下雨下雪天，乘客人数增加，周末职业学院学生出行较集中，节假日游客增多也会使得乘车人数增加等等。这些情况，需要公交公司要适时调整调度表。

表3 最优满意度的K39 路环形公交调度方案