一种基于RTK的遥测设备方位零位标定方法*

庞岳峰，霍文杰，张彬艳，马占顺

一种基于RTK的遥测设备方位零位标定方法*

庞岳峰，霍文杰，张彬艳，马占顺

（酒泉卫星发射中心 酒泉 732750）

针对现有遥测设备方位零位标定方法不满足机动测控需求的问题，提出一种基于旋翼无人机及实时动态RTK载波相位差分技术的遥测设备方位零位标定方法，推导测向关键算法，完成方位零位标定系统设计。通过采用数据同步匹配、异常值剔除及随机误差平滑等算法提高标定精度。测试及分析结果表明，采用该方法的方位零位标定精度可满足当前S频段和Ka频段遥测设备要求。

方位零位；旋翼无人机；RTK；遥测设备

引 言

实时动态RTK（Real-Time Kinematic）载波相位差分技术是基于载波相位观测值的实时动态定位技术，能够实时得到厘米级的定位精度[1,2]。其优势是在消除卫星轨道､钟差等残余误差[3,4]的同时可以实时估计电离层参数或采用高精度电离层改正数来削弱其影响[5]。

为了实现目标捕获与跟踪，车载遥测设备到达布站位置后，要标定天线方位零位偏差。当前，部分车载遥测设备无寻北功能，在外场执行任务时，现有的方位零位偏差标定方法不能兼顾标定精度和对机动测控设备快速标校的需求。针对该问题，研究了采用小型旋翼无人机及RTK载波相位差分技术来实现方位零位偏差修正的方法，完成了低成本、高精度遥测设备方位零位标定系统设计。

1 遥测设备方位零位偏差

2 基于RTK技术的方位零位标定系统设计

随着我国北斗系统全面建成，多系统多频信号RTK测向的优势更加明显，多频多模观测信号将大大减弱环境限制对RTK技术的影响，提高定位测向的精度和可用性[6-8]。单个GNSS接收机可确定位置，两个以上GNSS接收机可测向，据此原理设计基于RTK测向技术的遥测设备方位零位标定系统。

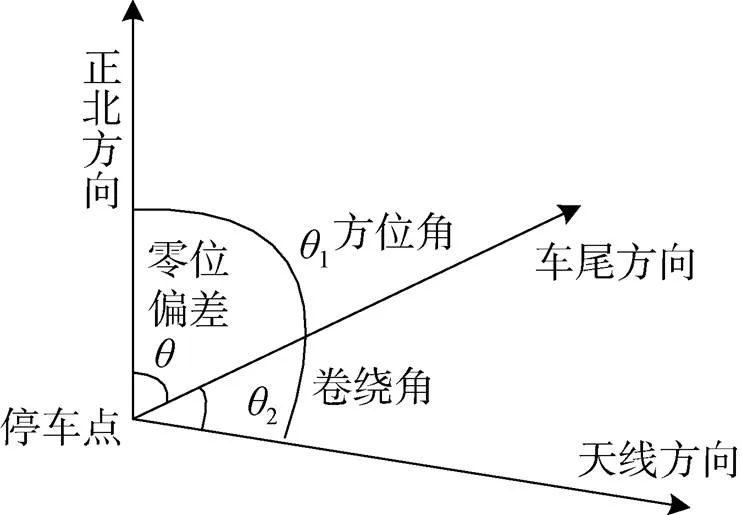
图1 方位零位偏差定义

2.1 方位零位标定系统组成

方位零位标定系统由旋翼无人机、RTK移动端、RTK基准站及数据处理终端组成。RTK基准站接基准天线和测向天线，可作为独立的测向单元使用。在遥测设备机械零位已校准的前提下，采用基准、测向天线测量出的设备车尾方位即方位零位偏差，由于这种测量方式基线较短，方位零位偏差测量精度在0.1°左右。

在需要进一步提高方位零位偏差测量精度时，采用无人机搭载RTK移动端的模式，RTK基准站基准、测向天线与RTK移动端位置信息进行联合解算完成。测量时将基准端天线安放在设备车体上，无人机搭载RTK移动端悬停，无人机动力及所搭载设备供电统一由无人机电源模块提供。采用数传电台把基准站的观测信息连续传给移动端，移动端通过电台接收观测数据，解算后实时得到三维坐标、基线长度和方位信息并向地面数据处理终端发送，同时数据处理终端通过电台发送无人机控制信息和信标设置命令。这种动态测量模式一般要求基准站和移动站同时接收到5颗以上的卫星，遥测设备方位零位标定系统组成如图2所示。

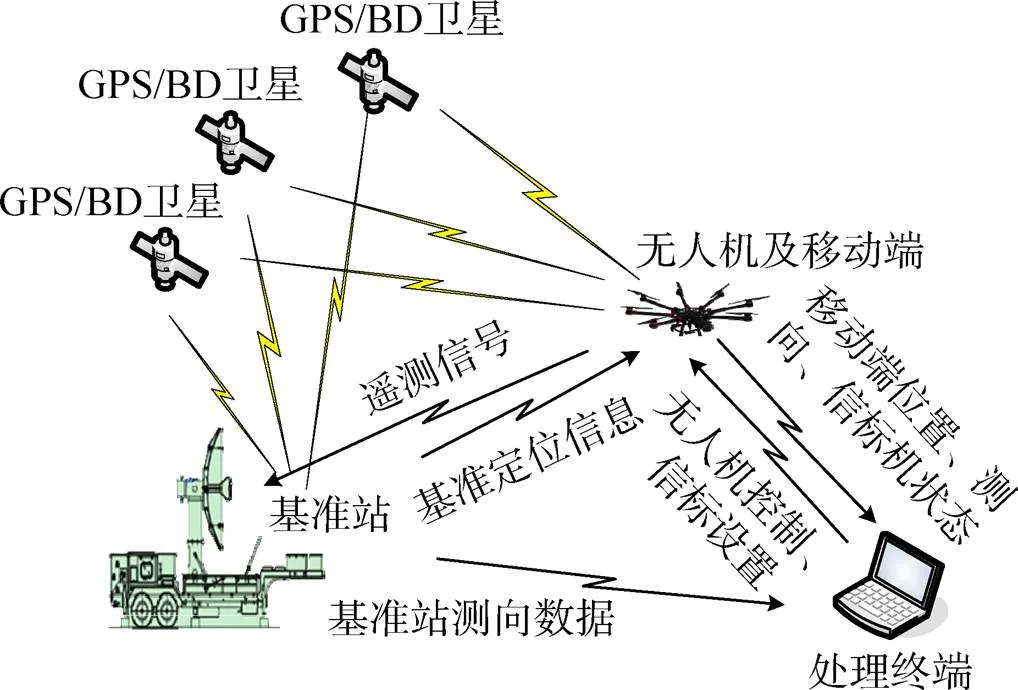
图2 方位零位标定系统示意图

基准站由主机、电源模块和电台组成。RTK板卡接收卫星信号，并接收所有卫星的RTK改正数据，然后按照RTCM的标准格式通过串口发送给数传电台，数传电台将改正数据发送给RTK移动端，供其进行实时载波相位差分。RTK基准站组成见图3、板卡实物见图5。

图3 RTK基准站组成示意图

无人机及RTK移动端由旋翼无人机、数传电台和RTK移动端组成。RTK移动端与RTK基准站主要有两方面区别:一是为减小移动端体积，延长电池使用时间，采用小型化设计；二是为方便野外作业，RTK移动端可选择采用无人机电源供电或外接电池供电。移动端接收卫星信号，并接收基准站发送的改正数据，进行实时载波相位差分，从而获得高精度基线测向。基准站和移动端的RTK板卡采用2018年上市的ZED-F9P芯片；数传电台采用XBee模块XPB9B，其传输实测距离大于1200m；Ingenic X1000微处理器完成相关运算和通信参数设置。无人机及RTK移动端组成关系如图4所示。

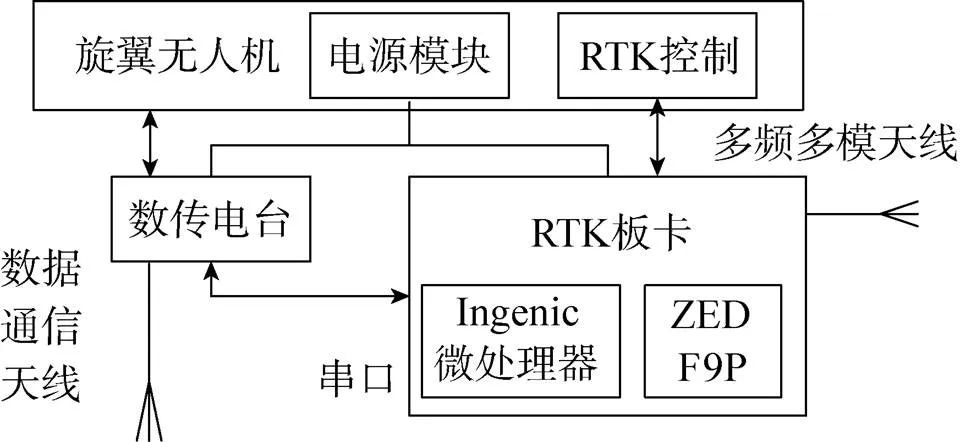
图4 RTK移动端组成示意图

图5 RTK基准站板卡实物图

2.2 测向解算流程设计

方位零位标定的前提是求解基线向量。计算的流程是首先利用三差求出近似的基线长度，再利用浮动双差法求出相位模糊度和基线矢量，将求得的相位模糊度凑整后，进行固定双差的解算，最后求解出精密基线向量[9-11]。移动端电台将接收到的改正数据通过串口送达开发板，移动端同时进行卫星观测、解算卫星位置，在选星及周跳探测后建立双差观测方程，然后通过确定单个天线的载波相位整周模糊度，进而确定双天线的载波相位整周模糊度单差，完成基线解算及精度计算后输出结果，处理结果发送模块将测向值通过串口发送给电台。基于载波相位的差分测向解算流程如图6所示。

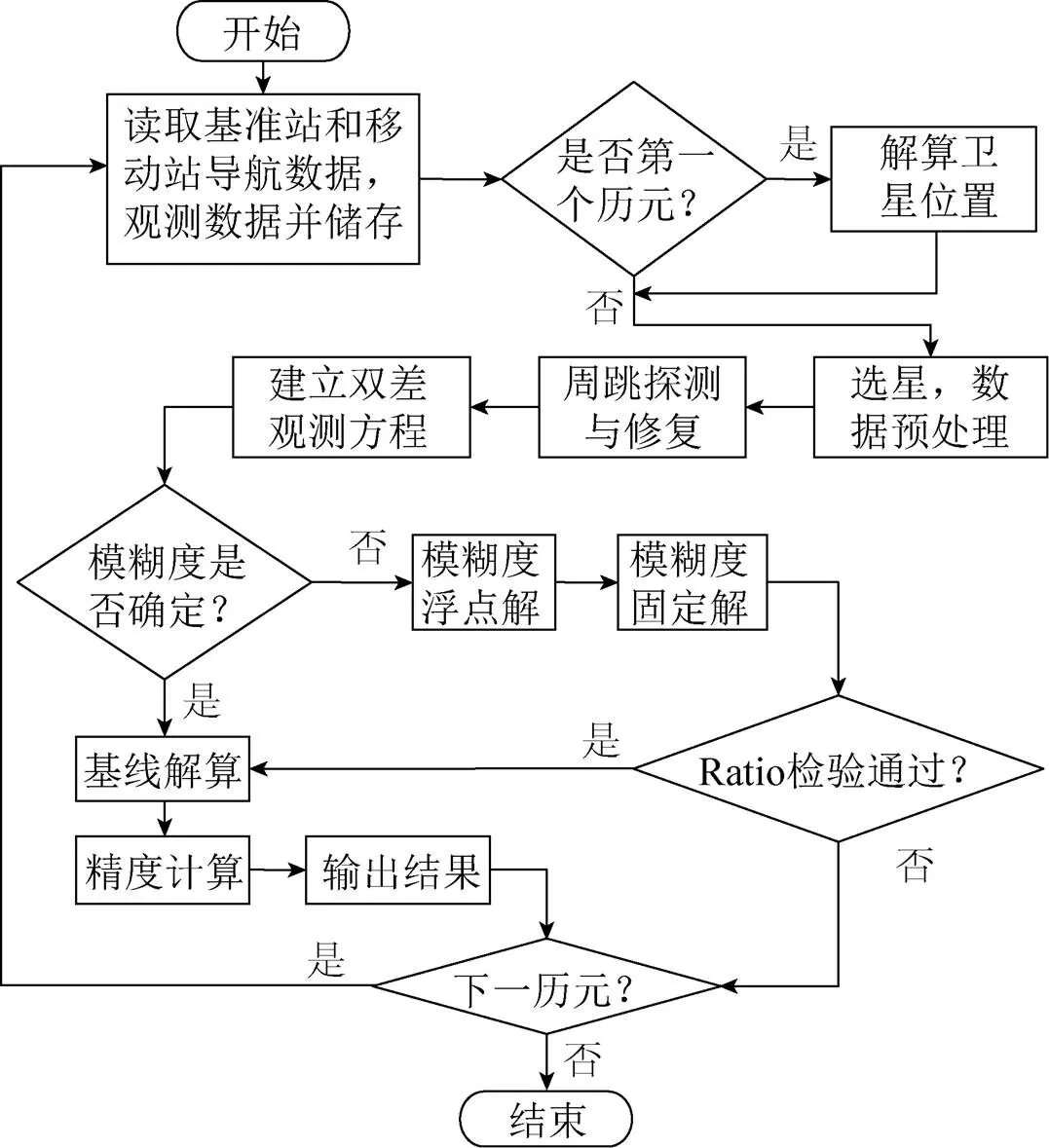
图6 基于载波相位差分的测向流程图

2.3 方位位标定方法

为提高测量精度，标定时需获得遥测天线站址中心相对于RTK基准天线的坐标，该参数可用几何学原理求得。方位零位标定时，基准端接基准天线和测向天线，两天线放置于遥测天线站址中心同一水平面内，与站址中心构成一个形状固定的三角形。基准和测向天线的位置通过测量得到，通过坐标转换以及三角形余弦定理，计算出遥测天线的相对站址坐标。无人机搭载RTK移动端和信标机在车体外一定距离悬停（图7），具体步骤如下：

图7 RTK测量标定方位零位示意图

①为遥测天线站址中心，事先已测定0、1长度和∠12角度。

②在天线载车1处放置RTK基准端基准天线，2处放置基准端测向天线，无人机搭载RTK移动端悬停，为无人机悬停点在12投影面上的投影点，载波相位差分测定1、2、1、2，依据1、2及0可解算出角度∠21（余弦定理）。

③三角形1中，已知两边一夹角（1、1、∠O1），计算出∠1。

④计算出天线相对于正北的方位角=∠1+∠1。

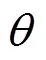
⑥控制无人机改变悬停位置，重复步骤②至步骤⑤，同样方法进行三次标定，取均值作为正式值。

3 方位零位标定系统关键算法

考虑无人机悬停精度易受外界条件影响，地面处理终端通过实时接收处理遥测设备伺服跟踪数据和RTK数据得出方位零位偏差，通过对遥测设备伺服跟踪数据和RTK数据的时间对齐、插值、野值剔除、平滑等算法提高测量精度。

3.1 RTK测向结果计算

RTK测向计算过程在数据处理终端实现，基准站及移动端定位信息通过电台发送至数据处理终端后由终端计算基线方向。由于遥测设备采用的是站心坐标系，需要进行坐标转换，具体步骤如下。

步骤1：坐标转换根据基准站记录的位置信息（经度c、纬度c、高程c），将它转换成地心固连系位置参数。具体公式如下：

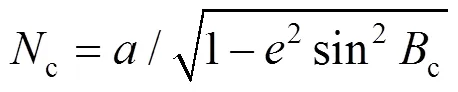
步骤2：将移动端由大地直角坐标系转换为移动端相对于基准站的东北天坐标(,,)公式如下：

步骤3：按照下式计算方位角、俯仰角和距离：

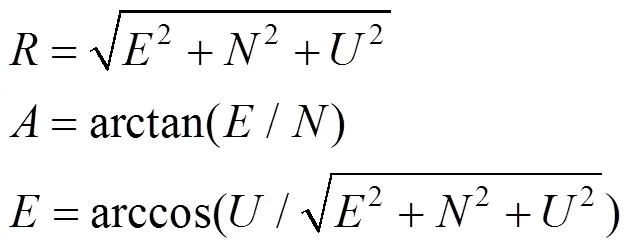
其中、具有方向性，的不同符号与方位角计算关系见表1，方位角度转换完成后，可以得到移动站相对于基准站的距离、方位和俯仰。

表1 方位角符号与计算关系

3.2 数据同步及匹配

由于RTK测量数据和遥测设备测角数据的传输频率不同，因此需进行数据同步和匹配。数据同步主要是为保证两数据时间的对齐，在此以移动端收星时间作为同步基准。遥测测角的采样率和RTK定位信息的采样率不同，并且在测量数据记录的过程中，可能会有某个点的数据没有被记录到，所以在时间对齐后还需要进行采样率匹配，以实现数据同步。

遥测测角的采样率为每秒20次，RTK测量数据传输为每秒5次，工程中还需要进行插值。RTK测量数据插值选择Neville算法，发挥其模型简单、计算量小的优势。具体插值方法可参考文献[12]，此处不再赘述。

3.3 测量数据随机误差平滑

平滑计算的目的是减小随机误差。遥测设备测量数据和RTK测量数据常带有随机误差，需要对测量数据进行平滑处理，以提高求解精度，本文采取多项式平滑方法。

设一组测量数据{i，i}（=1，2···，），（i为采样时间，i为测量数据），设多项式为

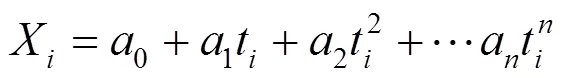
通过最小二乘法原理使偏差最小，即

根据求极值方法，将式（4）代入式（5），并求偏导数得出：

3.4 异常值的检测与剔除

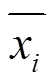
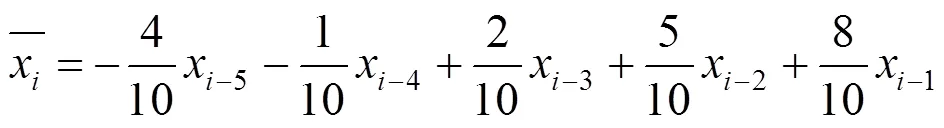
4 标定精度测试与分析

4.1 RTK测向精度

利用经过大地精确测量的点位，分别对96.2m、422.5m和807.7m基线下RTK测向精度进行了测试。96.2m基线精度为0.015°，422.5m基线精度为0.004°，807.7m基线精度为0.002°。结果表明测向精度与基线长度具有很大的相关性，基线越长计算的精度越高。为保证方位角计算的精确度，在有效距离内应尽量增加基线长度。

4.2 无人机悬停精度

对无人机搭载移动端悬停进行精度测试，无人机型号为大疆M600 pro，选择基线距离为800m左右的5个不同悬停位置进行测试，每次悬停时间180s，每秒记录5组数据。统计悬停时段的方位最大差及均方差，测试结果反映无人机悬停的水平方向均方差在0.026°~0.029°之间，见表2。

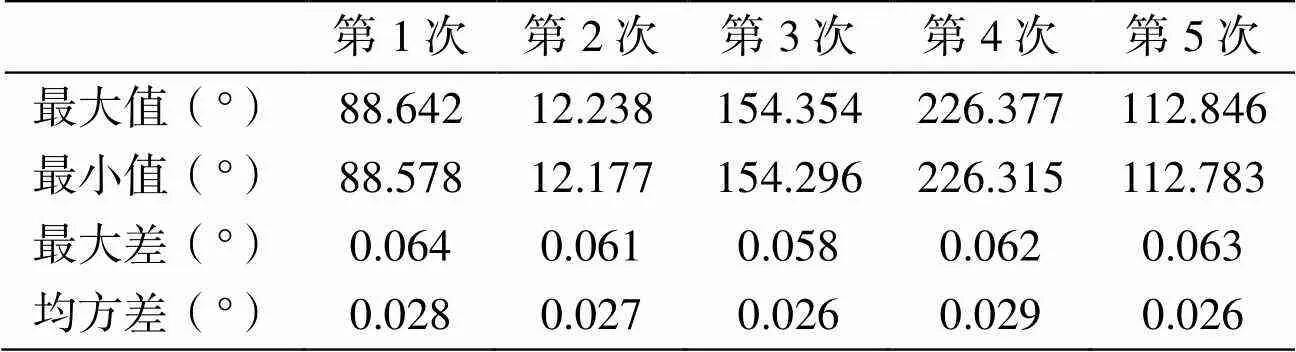
表2 无人机悬停精度（方位）

4.3 方位零位标定精度

在某S频段5.2m天线口径车载遥测设备上进行方位零位标定精度测试，测试前采用方位标对设备方位零位偏差进行校准，以此校准值为方位零位偏差真值，然后采用无人机搭载RTK移动端标定方法进行重新标定。选用两套设备进行精度测试，每套设备进行3次标定。3次标定时无人机悬停方位不同，但无人机与待标定设备距离均保持在800m左右，标定结果如表3。

表3 方位零位标定精度

进一步对图7中参与推导方位零位的各项误差进行分析，影响方位零位标定精度的变量为1及2误差、0及1测量误差、标校电视测量误差、无人机悬停水平精度和RTK移动端测量精度。已测得方位零位标定精度小于0.049°，满足现有S频段车载遥测设备的标定要求。大疆M600 pro悬停引入误差为0.029°，属于主要误差源。所以采用具有RTK差分功能的无人机后，方位零位标定精度还会明显提高。

5 结束语

移动端还设计了一个小型信标机。该信标机在方位零位标定功能中并未用到，但它是实现定向灵敏度标定和光电轴校准的必要器件，为后续功能拓展提供支持。本文精度测试所采用的大疆M600 pro无人机水平悬停精度为1.5m，如果采用具备RTK差分功能的无人机，其水平悬停精度可提高一个数量级，再通过改用高精度标校望远镜、加长基线距离、提高基准站天线安装精度等措施后，该标定系统方位零位标定精度可满足Ka频段遥测系统不大于0.01°的方位零位标定精度要求。

[1] 张宝成. GNSS非差非组合精密单点定位的理论方法与应用研究[J]. 测绘学报, 2014, 43(10): 1099. ZHANG Baocheng. Study on the oretical methodology and applications of precise point positioning using un-differenced and uncombined GNSS data[J]. Acta Geodaetica et Cartographica Sinica, 2014, 43(10): 1099.

[2] 王世进, 秘金钟, 李得海, 等. GPS/BDS的RTK定位算法研究[J]. 武汉大学学报信息科学版, 2014, 39(5): 621–625. WANG Shijin, MI Jinzhong, LI Dehai, et al. Real-time kinematic positioning algorithm of GPS/BDS[J]. Geomatics and Information Science of Wuhan University, 2014, 39(5): 621–625.

[3] 邹璇, 唐卫明, 葛茂荣, 等. 基于非差观测的网络实时动态定位方法及其在连续运行基准站跨网服务中的应用[J]. 测绘学报, 2011, 40(s1): 1–5. ZOU Xuan, TANG Weiming, GE Maorong, et al. Method of network RTK based on un-differenced observation corrections and its functional realization in cross CORS service[J]. Acta Geodaetica et Cartographica Sinica, 2011, 40(s1): 1–5.

[4] 鄢子平, 丁乐乐, 黄恩兴, 等. 网络RTK参考站间模糊度固定新方法[J]. 武汉大学学报信息科学版, 2013, 38(3): 295–298. YAN Ziping, DING Lele, HUANG Enxing, et al. A new method of ambiguity resolution in network RTK between reference stations[J]. Geomatics and Information Science of Wuhan University, 2013, 38(3): 295–298.

[5] LI Xingxing, GE Maorong, ZHANG Hongping, et al. The GFZ real-time GNSS precise positioning service system and its adaption for COMPASS[J]. Advances in Space Research, 2013, 51(6): 1008–1018.

[6] 姚宜斌, 胡明贤, 许超钤. 基于DREAMNET的GPS/BDS/GLONASS多系统网络RTK定位性能分析[J]. 测绘学报, 2016, 45(9): 1009–1018. YAO Yibin, HU Mingxian, XU Chaoqian. Algorithm and positioning accuracy analysis of GPS/BDS/GLONASSF network RTK nased on DREAMNET[J]. Acta Geodaetica et Cartographica Sinica, 2016, 45(9): 1009–1018.

[7] 何俊, 袁小玲, 曾琪, 等. GPS/BDS/GLONASS组合单点定位研究[J]. 测绘科学, 2014, 39(8): 124–128, 170. HE Jun, YUAN Xiaoling, ZENG Qi, et al. Study of GPS/BDS/GLONASS combined single point localization[J]. Science of Surveying and Mapping, 2014, 39(8): 124–128, 170.

[8] 李豹, 许江宁, 曹可劲, 等. 改进LAMBDA算法实现单频GPS整周模糊度快速解算[J]. 中国惯性技术学报, 2013, 21(3): 365–368. LI Bao, XU Jiangning, CAO Kejing, et al. A fast resolution of single frequency GPS integer ambiguity realized by improved LAMBDA algorithm[J]. Journal of Chinese Inertial Technology, 2013, 21(3): 365–368.

[9] WILLI D, ROTHACHER M. GNSS attitude determination with non-synchronized receivers and short baselines on board a spacecraft[J]. GNSS Solutions, 2017, 21(4): 1605–1617.

[10] 席志红, 耿更飞, 付存利. 一种基于双天线的北斗定位系统设计与实现[J]. 电子科技, 2014, 27(8): 101–104. XI Zhihong, GEN Gengfei, FU Cunli. Design and implement of Beidou positioning system based on double antenna[J]. Electronic Science and Technology, 2014, 27(8): 101–104.

[11] 吴玉平, 王建华, 杨钊. 基于双天线的高精度GPS定位测向系统及其在无人水面艇上的应用[J]. 计算机测量与控制, 2015, 23(4): 1330–1332. WU Yuping, WANG Jianhua, YANG Zhao. High precision GPS system based on double antennas and its application in unmanned surface vessel[J]. Computer Measurement & Control, 2015, 23(4): 1330–1332.

[12] 庞岳峰, 吴小东, 牛攀峰. 测控设备引导跟踪数据插值方法[J]. 电子科技, 2016, 29(11): 118–121. PANG Yuefeng, WU Xiaodong, NIU Panfeng. Measurement and control equipment tracking data interpolation method[J]. Electronic Science and Technology, 2016, 29(11): 118–121.

Azimuth zero position calibration method of telemetry equipment based on RTK surveying technology

PANG Yuefeng, HUO Wenjie, ZHANG Binyan, MA Zhanshun

（Jiuquan Satellite Launch Center, Jiuquan 732750, China）

In order to solve the problem that the azimuth zero position calibration method of current telemetry equipment doesn't meet the requirements of mobile measurement and control, this paper proposes an azimuth zero position calibration method based on rotor UAV and RTK surveying technology. The key algorithm of direction finding is deduced and the design of azimuth zero calibration system is completed. The calibration accuracy is improved by using the algorithms of data synchronization matching, outlier elimination and random error smoothing. The test result shows that the calibration accuracy of this method can meet the requirements of current telemetry equipment in S and Ka frequency bands.

Azimuth zero position; Rotor UAV; RTK; Telemetry equipment

V556.1

A

CN11-1780(2020)02-0068-07

酒泉卫星发射中心科研基金（2018ZKZ003）

2020-03-17

Email:ycyk704@163.com

TEL:010-68382327 010-68382557

庞岳峰 1980年生，硕士，工程师，主要研究方向为无线电测控技术。

霍文杰 1988年生，硕士，助理工程师，主要研究方向为航天工程。

张彬艳 1979年生，硕士，工程师，主要研究方向为信号与信息处理。

马占顺 1994年生，本科，助理工程师，主要研究方向为无线电测控技术。