一种便携式高精度超声流量仪

程 明，冯红亮，肖定国，韩德龙

一种便携式高精度超声流量仪

程 明1，冯红亮2，肖定国1，韩德龙2

（1 北京理工大学机械与车辆学院 北京 100081 2 北京遥测技术研究所 北京 100094）

研究一种超声波传播方向平行于液体流动方向的流量管和以此为基础的超声流量仪。针对流量系统的新型流量管结构推导两种流量算法并进行误差分析，其中一种算法可以减小由声速变化引起的误差，从而提高系统的测量稳定性，也为流量管的改进方向提供了思路。使用测显比曲线修正管道中流体流速分布不均匀的影响以提升测量准确性，试验证明，在测量范围内，系统测量的平均示值误差不超过0.2%。

超声流量计；流量算法；管道流体；流量计校准

引 言

超声波流量计作为一种流量测量仪表不仅应用于工业流体计量，在医疗、河流、海洋监测等计量领域也有广泛的应用[1]。超声波流量计可用于多种介质的流量测量，尤其对具有腐蚀性、高粘度、非导电等特性的流体流量测量有显著的优势[2]。

当超声波在流体中传播时，由于超声波速与流体流速在速度场上的叠加，导致超声波束在相同的距离内顺着流体流动方向传播与逆着流体流动方向传播所用的时间不一样，顺流时所需时间短，逆流时所需时间长[3]。时差法超声流量测量正是通过测量超声波在顺流与逆流中的时间差来计算流体的流动速度。为了降低顺逆流时间的测量误差，时差法需要超声波有较长的超声传播路程，才能在较大流速下也可以获得较高的测量精度[4]。目前，成熟的时差法和多普勒超声流量计多采用外夹式，时差法超声流量计在标定后测量精确度可以达到0.33%~0.5%[5]，多普勒超声流量计测量精确度能达到0.4%左右[6]。但是，外夹式超声流量计会遇到超声波经历多次界面反射和透射导致的相对信号较弱的问题以及管道状态较为复杂（管道厚度、腐蚀等情况各不相同）导致的应用均一性很难得到保障的问题。另外，实际使用的管道直径普遍较小，超声波传播路程很短，这些都会导致外夹式超声流量计测量误差较大，测量精度较低。

对于超声流量测量来说，准确获得流体流动速度是关键，但是管道流体的流速分布并不均匀，需要使用修正或者标定的方法获得不同速度下的截面平均流速，才能准确地得到流体的体积流量[7]。流量管中液体的流速分布与液体的流动状态有关，关于管道流体的截面流速分布也有不少实验、理论研究和仿真研究[8-10]，甚至根据经验公式给出了截面平均流速与最大流速之比随雷诺数变化的计算公式[11]。目前，关于截面平均流速的公式大多只能针对特定流动状态，且本身存在较大的误差，当流速变化范围大、跨越多种流动状态时，利用理论模型，根据测出的流速推算管截面流体的平均流速误差较大。

本文提出了一种基于超声波平行于液体流动方向的流量管（以下简称声束平行流量管）的超声流量仪，推导了该流量管结构下的两种流速流量计算方法。对比分析了两种算法的误差，并提出改进的方向，实现了测量时流体外部环境的统一和超声波在流体中传播时间的大幅提升，这有利于提高测量精度。使用标定曲线拟合公式的方式修正管道内径测量误差等系统误差和管道流体流速分布不均匀的影响，实现了较高的测量精度。

1 超声流量仪的系统组成

本文研究的超声波流量仪的特点是采用超声波平行于液体流动方向的流量管进行测量，测量系统的构成如图1所示。超声波探头A和探头B分别安装在流量管两端，两探头的声束轴与流体的流动方向平行。在流量管长度已知的情况下，探头A发射的超声波被探头B接收，可以计算获得超声波顺流传播时间；探头B发射的超声波被探头A接收，可以计算获得超声波逆流传播时间，得到的超声波的顺逆流传播时间可以用于计算液体流速流量值。

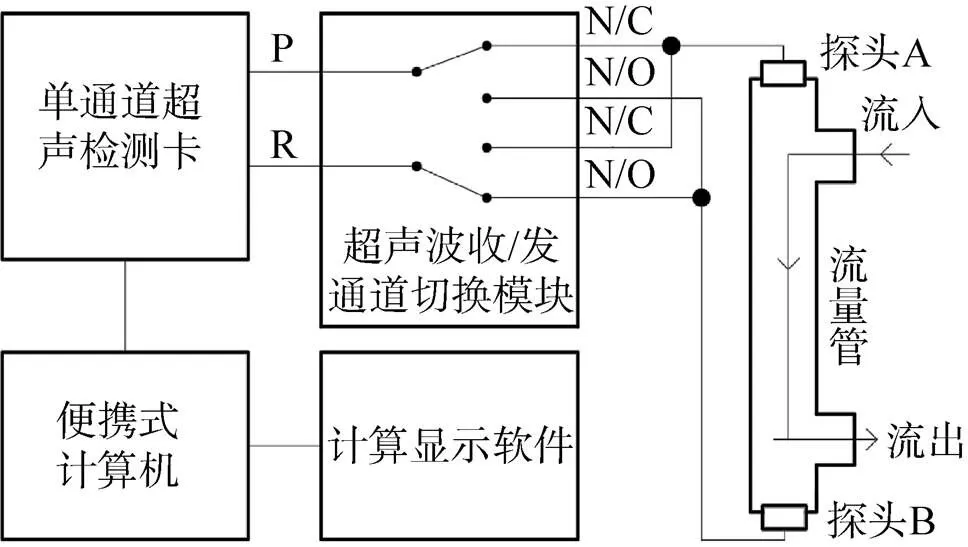
图1 超声流量仪的模块

超声流量仪主要组成部分包括：超声波探头（探头A、探头B）、超声波收/发通道切换模块、单通道超声检测卡、便携式计算机、流量管及相应的计算显示软件等。进行流量测量时，首先是探头A与超声检测卡的脉冲发射端接通，探头B与超声检测卡的脉冲接收端接通，探头A发射的超声波通过流量管中的流体被探头B接收。接收端口接收到超声波信号后，由集成在超声检测卡中的相应模块对接收到的脉冲信号进行处理（包括放大、滤波等）、A/D转换、以及数据采集等操作，计算出该方向超声波的传播时间。经过一次脉冲发射与接收后，通道切换模块在计算机和超声检测卡的控制下自动切换发射/接收通道，更改为探头B发射、探头A接收，重复进行上述动作进行第二次数据采集和计算。计算机通过以太网与超声检测卡进行通讯，对顺逆流条件下超声检测卡两次采集存储的数据进行运算处理得出流量值并显示，使用包括拉格朗日插值和互相关算法提高超声波传播时间的测量精度。该系统支持根据选用流量管型号和被测液体参数进行参数配置。

基于此超声流量测量系统进行了流速流量相关算法的研究和实验。该系统的工控系统部分进行了便携式集成设计，工控系统的仪器机箱尺寸为360mm×276mm×103mm，重量小于10kg，具有体积小、便携性操控性好、精度高的特点；流量管进行了模块化设计，两端安装超声探头的基座部分可以重复使用，流量管道部分可以选用预制的不同管径和长度的直管模块以满足不同的测量测试需求。

本文超声流量测量系统使用直管型号为DN20的流量管，直管长度为400mm。超声波探头选用了奥林巴斯公司的C540-SM型水浸探头，中心频率为1MHz。经过实验验证，对于水介质流体，在常温下、声程为800mm时，无论流量管中流体处于顺流还是逆流状态，超声流量测量系统依然可以获得稳定性良好、强度满足要求的超声信号。

2 流量管结构及流量计算原理

2.1 声束平行流量管结构

声束平行流量管的两端是对称结构，左端的结构如图2所示。该流量管的结构能够避免流体径向流速对测量的干扰，同时可以通过增大超声波传播距离来提高超声波顺逆流传播时差测量精度。流量管的整体长度随中间直管的长度不同而不同，本文使用的管道内径为20mm，直管长度可以在400mm~600mm范围内变化。

相较于外夹式“Z”型超声探头布置结构，新型流量管由于使用了平行于流动方向的超声探头布置方式，能在较小管径的直管中使用，同时也获得了较大的声程，因此在小管径小流量的测量应用中优势明显。

1-中间直管，2-连接器，4-45°三通，5-连接螺钉，6-超声探头，9-探头座，10-连接件，3,7,8-密封件

这两种流量管在具有相同的管道直径、静流声速、流速、只有布置结构不相同的理想情况下，二者关键参数的计算对比结果如表1所示。

由表1可知，在相同管径下，新型结构具有较大的声程，同时新流量管可以通过加长中间直流管的方式持续增大声程，进而增大顺逆流声时差，减小流量测量误差。

表1 同等条件下两种结构理论声时差计算

2.2 声束平行流量管的流量测量模型

声束平行流量管流速测量原理如图3所示。根据流量管的结构和探头安装方式，推导流量计算公式如下。

设在测量开始时流体充满整个流量管，流体从靠近探头A的进水口流入，经过流量管从靠近探头B的出水口流出。

图3 新型流量管流速测量示意图

先对测量直管段内的流体流动做简化处理：在靠近A、B探头两端的Aa段和bB段，近似认为流体处于静止状态；测量流体在直管ab段从左向右的轴线流动速度（进出水管道的轴心线与测量直管的轴心线相交与a、b两点）。基于以上简化处理，探头A发射的超声波被探头B接收时，得到顺流超声波传播时间为

式中，表示轴向流动距离ab，1表示两端流体近似静止段长度，c表示静流中声波传播速度，m表示流体的流速。

探头B发射、探头A接收时，得到逆流传播时间为

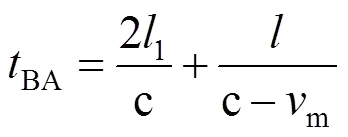
联立式（1）和式（2）得

由于流量管内流体的流速分布并不均匀，在不同流动速度下其流速沿管截面径向是变化的，因此，由式（4）计算得到的m在一般情况下不等于平均流速，而体积流量计算需要使用管截面内的平均流速，因此还需要对所测的流速m进行修正，才能较准确的计算出管道流量。管道的体积流量可由下式计算：

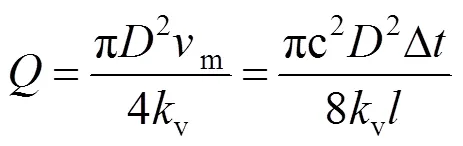
式中，为管道体积流量，为管道内径，v为修正系数。

静流声速c可利用流量管在静流条件下根据声传播时间和传播距离现场测出，测量计算得到静流声速为

式中，0为静流条件下超声波从探头A到探头B的或从探头B到探头A的传播时间。

此外，液体流速和流量还可用另一种改进的算式计算：

联立式（7）和式（8）得

2.3 误差分析

分析流量的计算式（5）可知，管道内径的测量误差和流速m的测量误差都会造成流量值的误差。管道内径的测量误差为固定值，可以使用标定的方法包含到修正系数v中；液体流动速度m的测量误差是流量测量的主要误差来源，因此主要分析速度m的测量误差。

对式（4）进行不确定度分析，可得相对不确定为

式中，为测得流速的不确定度，c为声速的不确定度，σAB和σBA分别为测得顺逆流声传播时间的不确定度。

管内液体流速为1m/s左右时声时差大约为300ns，系统对时间的分辨力为1ns，假定实验中流体温度为25℃，实验中温度升高5℃，将会导致声速增大12.4m/s，此时流速m的相对误差大约为1.2%。不考虑系统对时间的分辨力，只考虑温度变化时m的相对误差大约为0.8%。

由此可见，按式（4）计算流速时，由温度变化引起的静流声速c的变化对流速测量准确性的影响较大。

对式（9）进行不确定度分析，可得

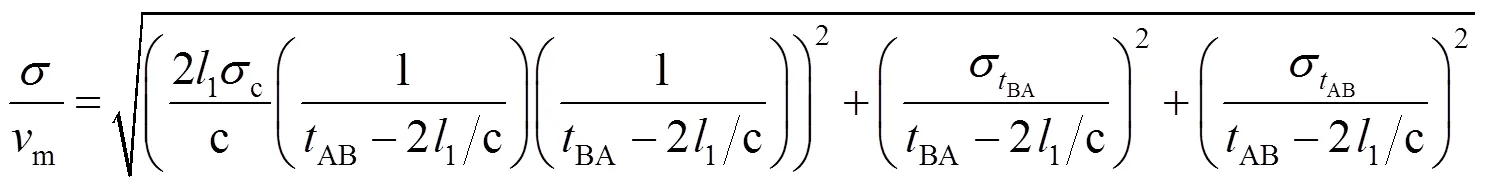
由式（12）可知，当1趋近于0时，由温度变化引起的静流声速c的变化对流速测量准确性的影响很弱，式（12）转化为

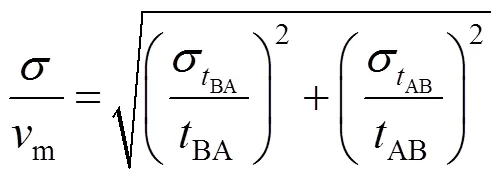
分析式（11）、式（12）和式（13）可知，在1足够小的情况下，式（12）表示的相对误差明显小于式（11），说明用式（9）计算流速比用式（4）计算流速更加稳定准确，更有利于消除由温度变化引起的静流声速c的变化对流速测量准确性的影响。本文系统采用式（10）计算流量。

3 试验和校准

3.1 系统标定

如上文所述，为了获得准确的平均流速，本文没有使用精度不高且有局限的仿真模型和经验公式，而是采用了标准流量装置标定的方法来确定修正系数v。

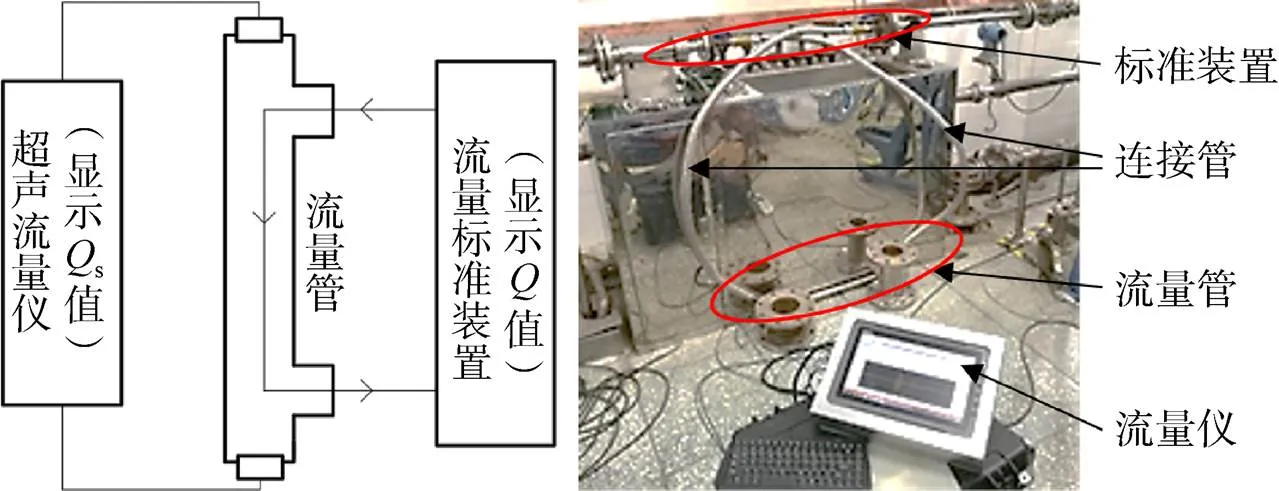
图4 标定系统模块和校准现场

标定的方法如图4所示，超声流量仪的流量管通过连接管接入流量标准装置的回路中，通过对比流量标准装置的流量和超声流量仪的显示流量来标定超声流量仪。用于标定的标准流量系统是采用计时称重法的流量测量系统。标定时使用的液体为纯水，温度为室温。由于计时称重法流量测量值准确性高，视为真实值。标定时记录不同流速下超声流量仪显示的流量值s和计时称重法测得的流量值，单位均为g/s计算它们的比值，该比值即为修正系数v，将v的倒数记为。对不同流量下标定得到的值与超声流量仪显示值s进行5次多项式拟合，并将拟合的方程用于修正测量结果，计算对应所测流量准确值。

标定得到的s曲线如图5所示。由于流量管直径的测量误差是固定值，所以该曲线的变化趋势也反映了流量管中截面等效平均流速a和最大流速m的关系。因此，超声流量仪配合高精度流量标准装置还可以进行流速分布的相关研究。

3.2 系统校准

为了评价超声流量仪测量液体流量的准确性，使用了中国计量科学研究院的0.01m3/h~200m3/h水流量基准装置进行评价，该装置的证书编号为国基证[2017]第015号，测量不确定度为0.05%，采用计时称重法计算流量。实验采用的液体为25.5℃的水，校准时的系统连接的表前直管长度大于40倍直径，呈V型安装，连接形式与标定时相同。

图5 Qs-k曲线

校准数据如表2所示，计时称重流量标准装置测得的流量值称为流量标准值，超声流量仪显示的流量值称为流量示值，示值误差为流量示值与流量标准值的差值和流量标准值的比值百分数。对覆盖测量范围的3个不同流量的测量准确性进行了评价，每个流量测量3次，记录每次的示值误差，3次示值误差的平均值为该流量测量准确性的评价结果。从表中可以看出，在整个测量范围内，3个流量测点的最大平均示值误差为0.17%，表明该超声流量仪在测量范围内有不高于0.2%的平均测量误差。

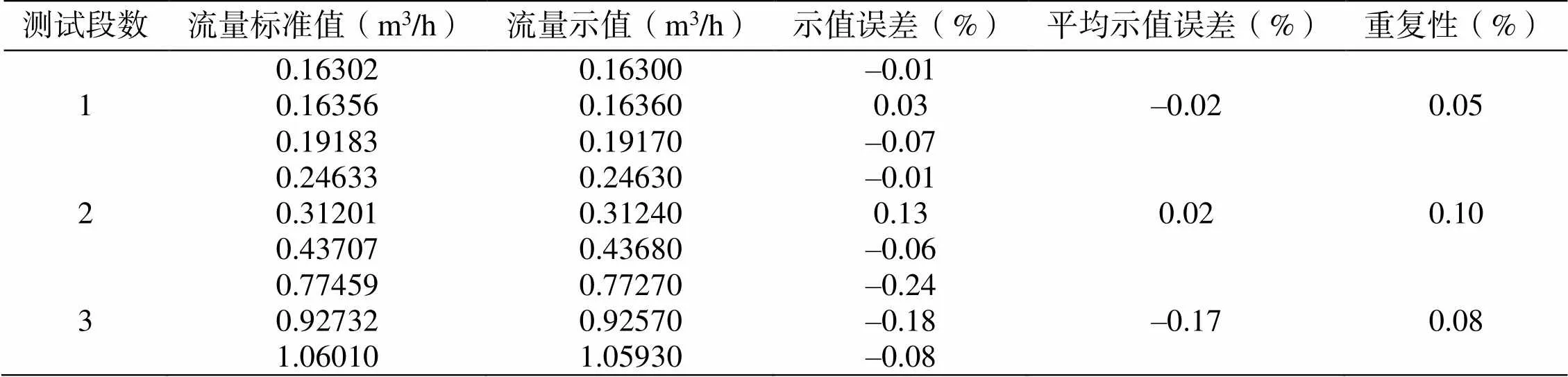
表2 校准评价数据

4 结 论

本文提出了基于声束平行流量管的超声流量仪，研究了在该流量管结构下流体流速的计算方法和流量计算修正方法，并使用高精度计时称重流量测量标准装置进行了校准和评价，得到结论如下：

①声束平行流量管超声探头平行液体流动方向的布置方式经过简化计算，能在较小管径上获得更长的声程和更大的声时差。这降低了测量误差，本文所述系统测量平均示值误差不高于0.2%。

②根据声束平行流量管的结构推导了时差法流量测量的流速计算方法，改进了流速计算算式，削弱了由温度变化引起的静流声速c的变化对流速测量准确性的影响，降低了测量误差。

③提出了标定得到s曲线，拟合s关系方程修正流速分布误差的方法，并分析指出该曲线不仅可以修正管道流体径向截面流速分布不均而造成的流速测量误差，还可用于管道内流体流速分布的反演。

[1] 薛蕾, 彭亮, 张超. 超声流量计在液体实流标定中的难点分析与解决方案[J]. 科技经济导刊, 2019, 27(10): 179. XUE Lei, PENG Liang, ZHANG Chao. Analysis and solution of difficulties in ultrasonic flowmeter calibration of liquid real flow[J]. Technology and Economic Guide, 2019, 27(10): 179.

[2] 李定川. 超声波流量计工程应用概述[J]. 智慧工厂, 2016(6): 84–88. LI Dingchuan. The composition and basic principle of ultrasonic flow meter and its application in production[J]. Smart factory, 2016(6): 84–88.

[3] SVILAINIS L. The time-of-flight estimation accuracy versus digitization parameters[J]. Ultragarsas, 2016, 63(1): 12–17.

[4] ORVATINIA M. Improvement of accuracy in multi-path ultrasonic flow meters[J]. Sensors & Transducers, 2019, 231(3): 1–9.

[5] 熊光德. 新型天然气超声波流量计量技术[J]. 天然气与石油, 2002(2): 57–61. XIONG Guangde. New technology of natural gas ultrasonic flow rate measurement[J]. Natural Gas and Oil, 2002(2): 57–61

[6] 王兴国, 张路鑫, 尧亮富, 等. 管道内流体流量的超声多普勒测量[J]. 电子测量与仪器学报, 2019, 33(10): 96–103. WANG Xingguo, ZHANG Luxin, YAO Liangfu, et al. Measurement of pipeline flow using ultrasonic Doppler method[J]. Journal of Electronic Measurement and Instrumentation, 2019, 33(10): 96–103.

[7] AGOLOM M O, LUCAS G, WEBILOR R O. Measurement of velocity profiles in transient single and multiphase flows using inductive flow tomography[J]. Flow Measurement and Instrumentation, 2018, 62: 246–254.

[8] 刘敦利, 胡鹤鸣. 圆形管道截面的流速分布实验与分析[J]. 仪器仪表标准化与计量, 2019(6): 43–45. LIU Dunli, HU Heming. Experiment and analysis on velocity distribution of circular pipeline cross-section[J]. Instrument Standardization & Metrology, 2019(6): 43–45.

[9] 宋振华. 超声流量计流场分析及导波流量检测方法研究[D]. 北京: 北京工业大学, 2017. SONG Zhenhua. Study on flow field analysis of ultrasonic flowmeter and flow measurement based on guided waves[D]. Beijing: Beijing University of Technology, 2017.

[10] ESCUE A, CUI J. Comparison of turbulence models in simulating swirling pipe flows[J]. Applied Mathematical Modelling, 2010, 34(10): 2840–2849.

[11] 何龙德. 管道截面的流速分布参数及其在涡街流量计标定中的应用[J]. 气动实验与测量控制, 1995(2): 67–73. HE Longde. Flow velocity parameters of pipeline section and its application in vortex flowmeter calibration[J]. Journal of Experiments in Fluid Mechanics, 1995(2): 67–73.

Portable high-precision ultrasonic flow measurement system

CHENG Ming1, FENG Hongliang2, XIAO Dingguo1, HAN Delong2

（1. School of Mechanical Engineering, Beijing Institute of Technology, Beijing, 100081, China; 2. Beijing Research Institute of Telemetry, Beijing 100094, China）

This paper presents a portable ultrasonic flow measurement system based on a new flow tube with the ultrasonic sensor parallel to the direction of liquid flow. Based on the new flow tube structure of the flow measurement system, two flow calculating algorithms are deduced and error analysis is performed. It is found that one of the algorithms can reduce the error caused by the change in sound velocity, which improves the measurement stability of the system and can also suggest ideas for improvement. This system uses the Qs-k ratio curve to correct the influence of uneven flow velocity distribution of the moving fluid. Within the measurement range, experiment shows that the error of the measured value of the system does not exceed 0.2%.

Ultrasonic flowmeter; Flow algorithm; Pipeline fluid; Flow meter calibration

TH814

A

CN11-1780(2020)02-0020-07

2020-03-20

Email:ycyk704@163.com

TEL:010-68382327 010-68382557

程 明 1994年生，硕士研究生，主要研究方向为超声流量测量和超声显微相关技术。

冯红亮 1976年生，高级工程师，研究方向为传感器及测试技术。

肖定国 1959年生，副教授，硕士生导师，主要研究方向为超声扫查检测与材料特性测试、超声显微检测与测量技术、超声检测仪器与换能器校准技术。

韩德龙 1994年生，硕士研究生，主要研究方向为测量及传感技术。