非线性刚度对微机械陀螺动态性能的影响*

佟向鹏，王 玺

非线性刚度对微机械陀螺动态性能的影响*

佟向鹏，王 玺

（海装驻北京地区第一军事代表室 北京 100076）

为了提高微机械陀螺的稳定性，研究自由振动状态下活动基座上L-L型双质量微机械陀螺的动态性能，建立微机械陀螺的数学模型，得到以幅值-相位为变量的运动微分方程的解，并给出这种解与轨道元素的联系。研究框架质量和弹性件非线性刚度对陀螺漂移量的影响，并给出数值例子。对所得到的解析关系式与曲线进行分析，作出关于系统性能的相应结论。

微机械陀螺；弹性件非线性刚度；自由振动；陀螺漂移

引 言

微机械陀螺技术是未来科学技术发展的方向之一，目前市场上基于MEMS（Micro Electro Mechanical System）技术研制的微机械陀螺已经占据了主导地位[1]，其主要优点是体积小、能耗少、产品造价低，而缺点是稳定性差[2-4]。因此，提高这类仪表的可靠性和技术指标是当前迫切需要解决的问题。

为了提高微机械陀螺检测输出信号灵敏度的稳定性，文献[5]首先求解了线性刚度下系统的稳态响应，进而采用多尺度法推导出非线性动力学方程的近似周期解。此外，文献[6]也研究了系统非线性刚度对陀螺性能的影响，并基于拉格朗日方程建立了系统的动力学方程，利用平均法进行求解，进一步分析了角度偏差对系统零偏、机械灵敏度和非线性度的影响。根据现有文献可知[7-10]，提高微机械陀螺精度指标的有效方法之一是研制多质量装置，例如国外的Bosch公司已经开始从事这类陀螺的研制工作，并且发现两个惯性质量的结构具有较好的技术指标稳定程度，但是，非线性动态效应对L-L型双质量微机械陀螺的动态性能具有明显的影响。因此，本文主要研究如图1所示的微机械陀螺动态模型[7-13]。

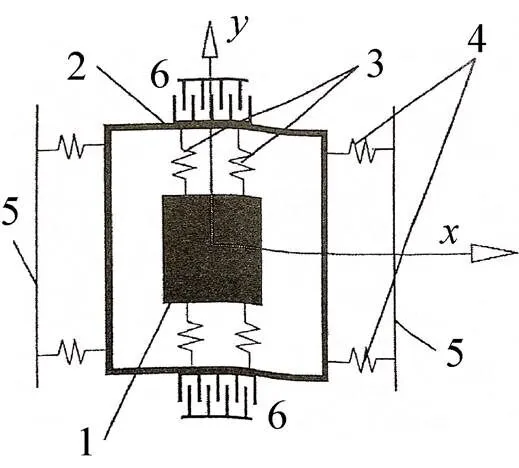
图1 微机械陀螺的动态模型

如图1所示，利用弹性内部支撑3（扭力杆）把敏感元件1固联到框架2上，这样的结构保证了敏感元件沿轴的一个自由度；利用扭杆4（外部）使框架2与基座5联结，这保证敏感元件沿轴的一个自由度。

扭杆的特殊形状保证了敏感元件主要工作在弯曲状态，但实际上该状态是观测不到的。利用电容系统激起敏感元件的振动框架2，并与基座5上的梳板一起构成了平板式电容器6。当框架振动时，梳板触点之间的间隙会发生变化，这就导致了电容的变化。本文的目的是分析自由振动状态下弹性元件非线性刚度对L-L型双质量微机械陀螺敏感元件性能的影响。

1 运动方程的建立

安装在基座上的“敏感元件-框架”系统，以常值角速度绕轴旋转，其动能表达式可以写为

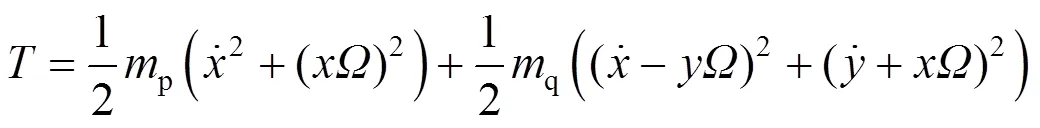
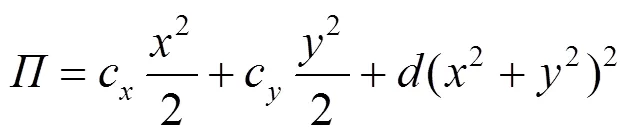
式中，c、c分别为扭杆在和轴上的刚度；为描述系统非线性形变的参数。

在这种情况下，系统的拉格郎日函数如下：

在基座角速度为常值的情况下，基于拉格郎日公式可以得到下面的方程组：

为了改善陀螺的共振特性，应该合理选择扭杆的弹性特性，使得针对广义坐标的共振频率相同。因此，假设系数c和c满足下面的关系式

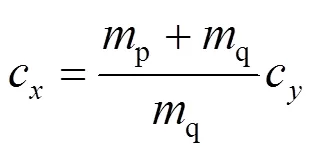
式中，为平板电容触点梳板之间间隙的大小。

因此，可以得到如下结果：

式中，

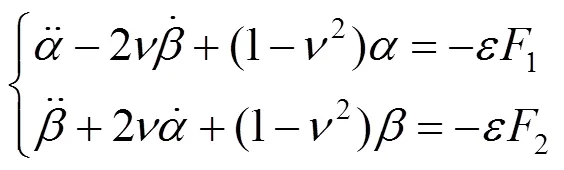
式中，

2 敏感元件动态性能分析

为了求解式（4），这里采用克雷洛夫-博戈留玻夫法，将式中变量转换为幅值-相位，因此，得到如下表达式

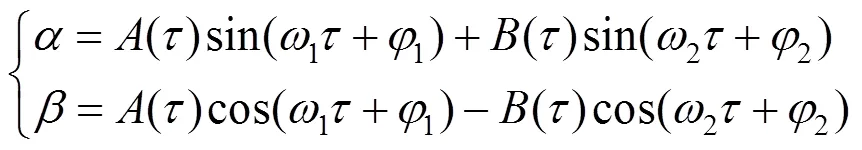
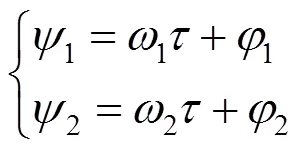
因此，基于式（11）可以进一步推导得到

基于式（11）和式（13），利用兼容性条件可以得到如下表达式：

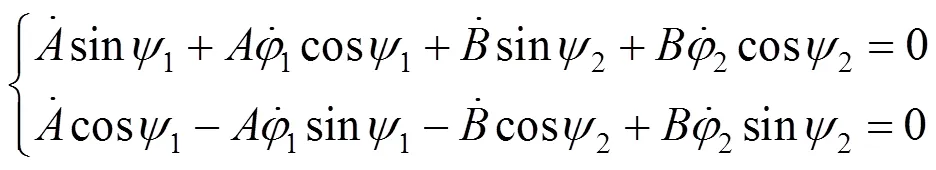
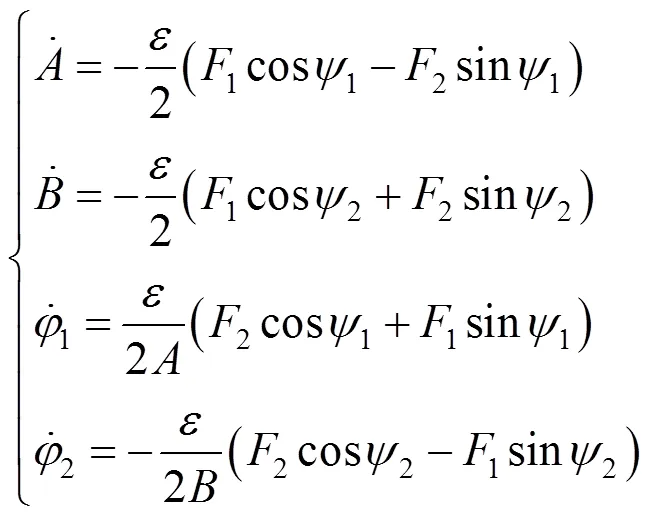
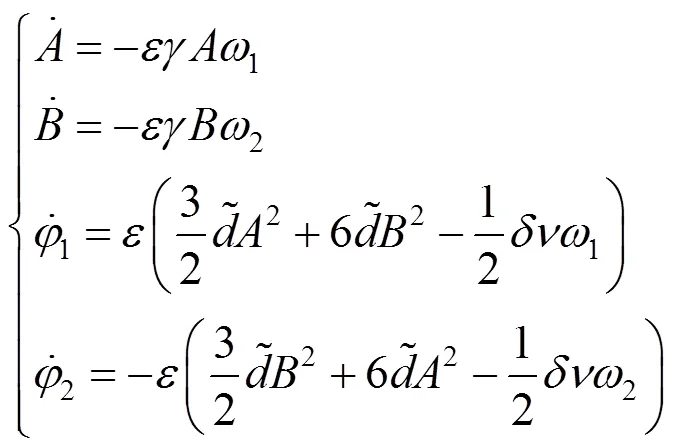
因此，基于式（17）可以得到解的形式为

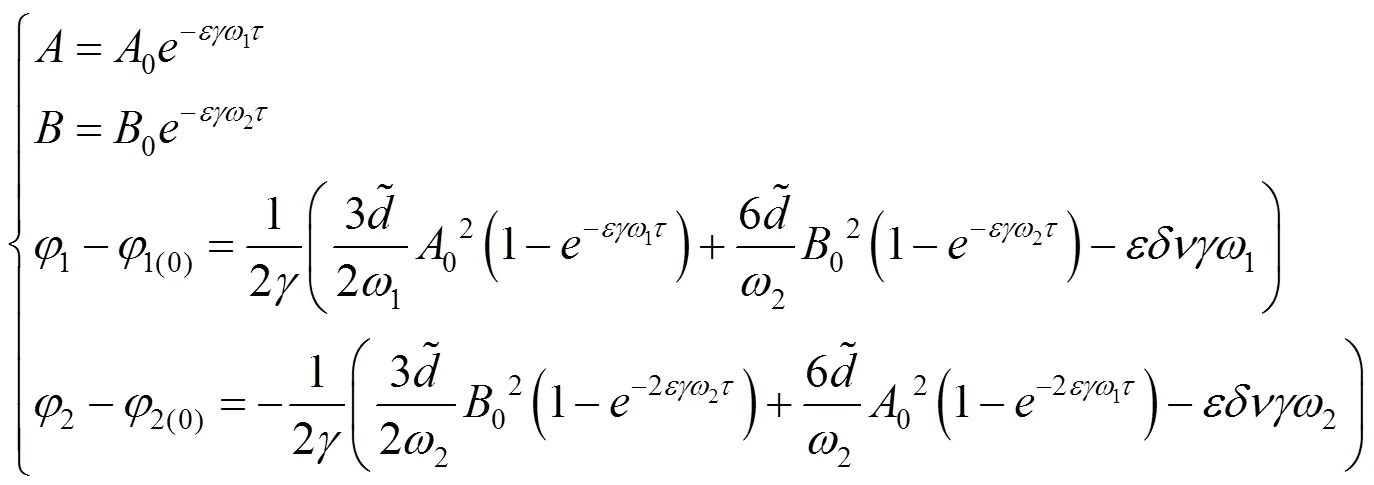
式中，为波图的定向角；，决定波图中仪表漂移大小的附加缓慢进动；为相位，描述振动频率变化，并给出点在开始时刻的位置；r、k为振动的基波和二次波的标准化振幅，即椭圆的半主轴，如图2所示。

3 数值例子

图3 数值仿真结果

4 结束语

本文主要研究了L-L型双质量微机械陀螺的数学模型，并且在模型中考虑了系统的黏性摩擦、基座角速度和自由振动状态下弹性件的非线性刚度。通过一个数值例子表明，非线性刚度和框架质量的存在会对确定进动角的精度以及振动相位的变化产生明显影响。

[1] 杜宜璋, 常洪龙, 苑伟政, 等. 多环谐振微机械陀螺的研究现状及发展趋势[J]. 导航与控制, 2019, (4): 1–10. DU Yizhang, CHANG Honglong, YUAN Weizheng, et al. Research status and development trend of multi-ring resonant micromechanical gyroscope[J]. Navigation and Control, 2019, (4): 1–10.

[2] NESTERENKO T G, VTORUSHIN S E, BARBIN E S, et al. Effect of the anisotropy of monocrystalline silicon mechanical properties on the dynamic characteristics of a micromechanical gyroscope [J]. IOP Conference Series: Materials Science and Engineering, 2015, 81: 012096.

[3] 文永蓬, 尚慧琳. 微陀螺动力学建模与非线性分析[J]. 振动与冲击, 2015, 34(4): 69–73. WEN Yongpeng, SHANG Huilin. Dynamical modeling and nonlinear analysis of microgyroscope[J]. Journal of Vibration and Shock, 2015, 34(4): 69–73.

[4] 温姣. 一种新型微机械陀螺仪的结构与检测系统研究[D]. 成都: 电子科技大学, 2011. WEN Jiao. Research on the structure and detection system of a new micromechanical gyroscope[D]. Chengdu: University of Electronic Science and Technology of China, 2011.

[5] 郝淑英, 李伟雄, 李会杰, 等. 驱动刚度非线性对双检测微陀螺性能的影响[J]. 振动与冲击, 2019, 38(14): 131–137. HAO Shuying, LI Weixiong, LI Huijie, et al. Effect of driving stiffness nonlinearity on the performance of a double sense-mode micro gyroscope[J]. Journal of Vibration and Shock, 2019, 38(14): 131–137.

[6] 张利娟, 李欣业, 张华彪. 角度偏移对微机械陀螺系统响应特性的影响[J]. 振动与冲击, 2019, 38(7): 65–70. ZHANG Lijuan, LI Xinye, ZHANG Huabiao. Influences of angular deviation on response characteristic of a MEMS gyroscope system[J]. Journal of Vibration and Shock, 2019, 38(7): 65–70.

[7] 殷勇, 王寿荣, 王存超, 等. 一种双质量硅微陀螺仪[J]. 中国惯性技术学报, 2008, 16(6): 703–711. YIN Yong, WANG Shourong, WANG Cunchao, et al. Dual-mass silicon micro-gyroscope[J]. Journal of Chinese Inertial Technology, 2008, 16(6): 703–711.

[8] 殷勇, 王寿荣, 王存超, 等. 结构解耦的双质量微陀螺仪结构方案设计与仿真[J]. 东南大学学报(自然科学版), 2008(05): 182–186. YIN Yong, WANG Shourong, WANG Cunchao, et al. Structural scheme design and simulation of structure-decoupled dual-mass MEMS gyroscope[J]. Journal of Southeast University (Natural Science Edition), 2008(5): 182–186.

[9] 屈玉丰. 双级解耦微机械陀螺的结构设计及特性研究[D]. 合肥: 合肥工业大学, 2008. QU Yufeng. A study of the doubly decoupled micromachined gyroscope design and its characteristics[D]. Hefei: Hefei University of Technology, 2008.

[10] 李凌宇, 卢翌, 陈兴, 等. 微机械陀螺仪设计与研究[J]. 电子科技, 2013, 26(9): 172–176. LI Lingyu, LU Yi, CHEN Xing, et al. Design of and research on MEMS gyroscope[J]. Electronic Science and Technology, 2013,26(9): 172–176.

[11] 郝燕玲, 刘博, 史宏洋. 新型反相位驱动双解耦微机械陀螺设计[J]. 哈尔滨工业大学学报, 2014, 46(9): 105–110. HAO Yanling, LIU Bo, SHI Hongyang. The novel design of anti-phase double-decoupled micromachined gyroscope[J]. Journal of Harbin Institute of Technology, 2014, 46(9): 105–110.

[12] 曹慧亮, 李宏生, 申冲, 等. 双质量硅微机械陀螺仪带宽拓展系统设计[J]. 中国惯性技术学报, 2016, 24(2): 218–223. CAO Huiliang, LI Hongsheng, SHEN Chong, et al. Bandwidth expanding system design of dual-mass silicon MEMS gyroscope[J]. Journal of Chinese Inertial Technology, 2016, 24(2): 218–223.

[13] 李锦明, 郭慧芳, 刘俊. 一种三框架电容式硅微机械陀螺结构设计与仿真[J]. 传感技术学报, 2008(2): 68–70. LI Jinming, GUO Huifang, LIU Jun. Design and simulation of a three-frame capacitive micromechanical gyroscope[J]. Chinese Journal of Sensors and Actuators, 2008(2): 68–70.

Effect of nonlinear stiffness on dynamic performance of the micromechanical gyroscope

TONGXiangpeng, WANG Xi

（First Military Representative Office of the Naval Equipment Department in Beijing, Beijing 100076, China）

In order to improve the stability of the micromechanical gyroscope, the dynamic performance of the L-L type two-mass micromechanical gyroscope on the movable base in free vibration state is studied, and the mathematical model of the micromechanical gyroscope is established to obtain the solution of the motion differential equation with amplitude-phase as the variable, and the relation between the solution and the orbital elements is given. In addition, the effects of the frame mass and the nonlinear stiffness of elastic parts on the gyro drift are studied, and a numerical example is given.Finally, the obtained analytic relation and curveare analyzed, and the corresponding conclusions about the system performanceare drawn.

Micromechanical gyroscope; Nonlinear stiffness of elastic parts; Free vibration; Gyro drift

TH113

A

CN11-1780(2020)02-0010-05

军内科研项目

2020-03-20

Email:ycyk704@163.com

TEL:010-68382327 010-68382557

佟向鹏 1982年生，本科，高级工程师，主要研究方向为MEMS惯性器件和微机电系统研究。

王 玺 1994年生，硕士研究生，助理工程师，主要研究方向为微机电系统研究。