路基冻胀-融化-沉降循环作用下高速铁路板式无砟轨道伤损演化与变形分析

林士财

(陕西省铁道及地下交通工程重点实验室(中铁一院), 西安 710043)

1 概述

自哈(哈尔滨)大(大连)高速铁路通车以来，我国严寒地区高速铁路运营里程已超过3 000 km[1-3]。严寒地区铺设无砟轨道时，冬季气温的急剧降低导致路基内水分冻结成冰，路基形成冻胀，轨道结构抬升上拱；春季气温回暖，路基进入融化阶段，轨道结构下沉回落，且在列车动荷载作用下易形成路基不均匀沉降问题。路基冻胀-融化-沉降的周期性循环，易引起轨道板、底座板等混凝土结构开裂，并加速轨道和路基结构的破坏，导致轨道结构功能性和耐久性降低；易造成底座板与基床表层之间产生周期性的离缝甚至脱空，给高速列车运行舒适和安全带来直接隐患；导致轨道结构出现大变形，几何形位发生恶化，影响高速列车运行舒适性，甚至危及行车安全。

目前，国内外诸多学者对路基变形问题进行了大量研究。赵国堂[1]结合实测数据给出了路基冻胀基本波形曲线，基于冻胀计算模型分析了路基冻胀对轨道平顺性及轨道结构变形的影响，并提出了严寒地区路基冻胀管理标准的确定方法；蔡小培等[4]探讨了冻胀位置和不同冻胀条件下轨道结构变形及离缝特征，并基于内聚力模型分析了层间黏结强度及底座板刚度对层间离缝演化发展的影响；杨国涛等[5]探讨了不同冻胀变形下轨道变形传递规律，分析了路基冻胀对列车行车及轨道结构动力学特性的影响，并基于静动力分析提出了路基冻胀控制标准；赵国堂等[6]基于轨道检查大数据，结合数据处理方法对路基冻融前后轨道平顺性进行了分析；ZHANG等[7-12]对路基沉降或冻胀的发展机制、预测等进行了研究；肖威等[13-16]分析了路基不均匀沉降对轨道结构受力变形及平顺性的影响；徐庆元等[17-20]从不同角度出发建立了路基上无砟轨道结构动力模型，分析了轨道结构的动力学特性，并就不同的评价指标提出了相应的沉降控制标准。

可见，现有研究对路基冻胀或路基不均匀沉降问题进行了细致、深入的研究，但多从单方面角度出发，对路基连续性变形较少考虑；且现有文献多基于线弹性分析理论，难以准确反映路基变形过程中轨道结构的服役状态；不同加载位置对轨道结构的影响研究相对不足。为此，基于有限元分析和混凝土塑性损伤模型，建立路基上CRTS I型板式无砟轨道静力分析模型，研究路基冻胀-融化-沉降循环作用下，轨道结构受力和变形特征及伤损演化发展规律，以期为高速铁路板式无砟轨道的养护维修提供参考依据。

2 有限元模型建立

2.1 模型建立与说明

路基上CRTSⅠ型板式无砟轨道由钢轨、轨道板、砂浆层、底座板及凸型挡台等部件组成。钢轨类型选取为我国高速铁路采用的标准60 kg/m钢轨，以空间点支承梁单元进行模拟，弹性模量E=210 GPa；钢轨和轨道板之间通过连接器单元来模拟扣件的支承和约束作用，考虑其垂向、横向和纵向刚度，刚度取值分别为50，30 kN/mm和30 kN/mm，扣件间距为标准扣件间距，取值0.629 m；轨道板、砂浆层、底座板和路基等均采用实体单元模拟；底座板每隔3块轨道板设置1道横向伸缩缝，缝宽20 mm，考虑最不利情况，将伸缩缝处做断开处理。为避免边界条件的影响，模型长度取值100 m。所建立的有限元模型如图1所示。各结构层基本参数如表1所示。

图1 CRTSⅠ型板式无砟轨道-路基静力模型

表1 CRTSⅠ型板式无砟轨道基本参数

2.2 接触及边界条件设置

在定义接触关系时，轨道板和砂浆层与凸型挡台间、底座板与基床表层间均设置为可分离的摩擦接触，该约束可合理模拟层间离缝甚至脱空现象；轨道板与砂浆层、砂浆层与底座板间则采用绑定约束，不考虑层间相对位移及法向分离。

边界条件统一设置为：约束轨道各结构层端部的纵横向位移；而基床底部则采用全约束。

本文未考虑路基变形对其弹性模量等基本参数的影响，仅考虑一次循环荷载作用。对于实体路基，通过对基床表层施加强制位移边界条件模拟路基冻胀-融化-沉降作用，其变形曲线采用单波余弦曲线，各阶段表达式如下

(1)

式中：L为变形波长；z0为变形起始位置；z为变形发生位置；f为变形幅值。

冻胀-融化-沉降连续加载过程如图2所示。说明如下：本文以变形幅值作为输入条件来考虑路基的连续性变形，未考虑过程中波长的改变，每个分析步对应的幅值变化为2 mm，为便于表达，将横轴定义为分析步时间轴。

图2 冻胀-融化-沉降加载曲线

路基变形波长、峰值和发生位置对轨道结构服役状态均具有一定影响[1]。以峰值作用于伸缩缝位置为例，东北地区冻胀量主要集中在0～20 mm，约占所有冻胀量的90%[21]。因此，冻胀幅值设定为20 mm，为便于说明轨道板等部件的伤损演化情况，路基变形波长设定为5 m。

2.3 混凝土塑性损伤模型(CDP)

CDP模型是表征混凝土结构非弹性行为的一种连续的、基于塑性的损伤模型，可准确地表征混凝土结构在循环荷载作用下所产生的不可逆损伤行为[22]。轨道板和底座板的一般本构关系由文献[23]所建议的应力-应变关系确定，但为了输入适用于CDP模型的本构关系，需要对一般本构关系进行修正。

由于混凝土多为受拉开裂，采用以开裂时的割线模量为弹性阶段的无损伤弹性模量E0，如式(2)所示，而后反推受压弹性极限分界点的方法，确定修正后的混凝土应力-应变关系

(2)

式中ftk——混凝土抗拉强度标准值；

εtk——与ftk对应的混凝土峰值拉应变。

修正后的受拉本构关系如下

(3)

式中,x=ε/εtk，y=σ/ftk，αt为混凝土单轴受拉应力—应变曲线下降段的参数值。

修正后的受压本构关系

(4)

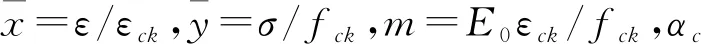
在CDP模型中，需要以离散点的方式输入“应力-非弹性应变/开裂应变-损伤因子”的对应关系，从而确定轨道板和底座板的混凝土塑性损伤本构关系，具体参数可由图解法确定[22]。

3 影响规律分析

3.1 伤损影响规律分析

图3罗列了部分幅值条件下底座板的最大主塑性应变云图。冻胀幅值、融化幅值和沉降幅值分别以D、R和C表示。

图3 底座板的最大主塑性应变云图

由图3可以得出如下结论。

(1)路基连续变形过程中，当幅值作用于伸缩缝时，轨道板未见塑性损伤。原因在于，路基冻胀过程中，轨道板上表面受压，底座板下表面受拉，压应力作用不足以导致轨道板萌生损伤；而路基沉降过程中，轨道板和底座板的应力状态与前述相反，轨道板上表面受拉，但考虑到轨道板在跟随性变形过程中变形能力有限，拉应力作用亦不足以导致其萌生损伤。

(2)路基冻胀过程中，底座板损伤萌生于伸缩缝两侧第1块轨道板板端接缝处，且初始损伤沿接缝横向分布并绕过凸型挡台，如图3(a)所示。原因在于此处轨道板与底座板间的挤压作用较强，拉应力较大所致。

(3)路基持续冻胀，底座板损伤逐渐扩展、加剧并蔓延至凸性挡台下方；此外，导致凸性挡台根部形成明显塑性区域，如图3(b)所示。

(4)路基融化回落及沉降过程中，底座板的塑性损伤状态相对稳定，损伤区域未见明显扩展。

3.2 轨道不平顺影响分析

路基变形后，轨道各结构层的垂向位移保持良好的同步性[1，16]，路基变形最终传递至钢轨，并形成轨道不平顺。图4为路基冻胀-融化-沉降循环作用下，轨道不平顺的波形曲线。图5为路基变形幅值对轨道不平顺幅值的影响规律。

图4 轨道不平顺的波形曲线

图5 轨道不平顺幅值随路基变形的变化规律

结论如下。

(1)路基冻胀-融化-沉降循环作用导致大范围的轨道不平顺，路基变形波长L为5 m时，底座板的非连续性导致轨道不平顺长度达10 m以上。

在冻胀和融化回落过程中，由于路基变形波长较小，且考虑到钢轨抗弯刚度的存在，轨道不平顺幅值略小于路基变形幅值，如D=8 mm时，轨道不平顺幅值为7.01 mm。

(2)路基冻胀过程中，轨道不平顺幅值随路基变形幅值的增加呈线性增加的变化趋势，线路平顺性逐渐恶化。根据过往研究经验，高速列车通过时，轮轨冲击作用将逐渐增大，轮轨力、脱轨系数和轮重减载率及车体的垂向振动加速度增加，行车安全性和舒适性逐渐降低[24]。

(3)春季气温回升，路基融化回落，钢轨在轨下结构的牵引下逐渐恢复至初始状态，轨道不平顺幅值呈线性回落的变化规律，线路平顺性得到逐步改善，行车安全性和舒适性逐渐恢复。

但值得注意的是，在路基回落至4 mm以下时，相对于冻胀过程同一幅值条件，二者的轨道不平顺波形曲线未完全重合，在冻胀峰值两侧，钢轨的回落滞后于基床表层，钢轨存在部分残余变形，如：D=4 mm和D=2 mm条件下，残余变形分别为0.37 mm和0.32 mm，当路基恢复至初始状态，钢轨残余变形为0.08 mm，其根本原因在于底座板的塑性变形。

(4)路基进入沉降阶段后，轨面不平顺波形由上凸形式变化为下凹形式，在端部上拱位置，由于塑性区的存在，轨道不平顺曲线出现异常性变化，打破了轨面波形的连续性。

随路基沉降幅值的增加，轨面波形曲线无明显差异，轨道不平顺幅值亦无明显变化，原因在于轨道结构的变形能力达到极限。但随着沉降幅值的增加，势必导致底座板与基床表层间形成大宽度的离缝甚至脱空，影响行车舒适性，乃至安全性。

3.3 离缝影响分析

图6为路基冻胀-融化-沉降循环作用下，底座板与基床表层之间的离缝纵向分布，Ln代表峰值位置左侧第n块轨道板，Rn代表峰值位置右侧第n块轨道板。可以得出如下结论。

图6 离缝纵向分布

(1)路基持续冻胀过程中，底座板与基床表层间的离缝分布表现为：由冻胀峰值向其两侧过渡，底座板与基床表层间的离缝宽度先增大后减小，冻胀位置远端离缝宽度为0；离缝主要分布于L1、L2和R1、R2底部，而最大离缝位于L1和R1底部，与路基变形起始位置具有一定的同步性，且离缝宽度随冻胀幅值的增加而增大。

由前述分析，不难判断，路基融化回落阶段，底座板与基床表层间的离缝纵向分布与冻胀过程分布无明显差异性。

(2)路基处于沉降阶段，底座板与基床表层间的离缝分布表现为：由沉降峰值向其两侧过渡，底座板与基床表层间的离缝宽度逐渐减小，至沉降远端离缝宽度为0；离缝主要分布于L1和R1底部，最大离缝位于沉降中心，且离缝宽度随冻胀幅值的增加而增大。

图7为路基冻胀-融化-沉降循环作用下，底座板与基床表层间的最大离缝宽度的连续变化曲线。图中F-L和F-R分别表示伸缩缝的左、右侧的最大离缝位置，对应具体位置详见图7。

图7 最大离缝宽度变化规律

路基在持续冻胀过程中，F-L和F-Z处的最大离缝宽度随冻胀幅值的增加而呈线性增加，离缝现象逐渐加剧。如D由2 mm增至6 mm，离缝宽度分别由0.50，0.92 mm增至2.54，2.52 mm，离缝宽度的非同步性增长系由底座板的非对称性所致。

路基融化回落阶段，离缝宽度逐渐减小、回落并最终闭合，离缝现象得到逐渐缓解。相比于冻胀过程中同一变形幅值条件，离缝宽度略大，如D=4 mm和R=4 mm，F-L处的离缝宽度分别为1.40 mm和1.75 mm。

路基进入沉降阶段后，F-L和F-Z处的离缝由闭合状态再次逐渐张开，但随沉降幅值的增加，最大离缝宽度增幅极小，增幅介于0.03～0.06 mm；而沉降峰值位置，离缝宽度随沉降幅值的增大呈线性增大趋势，且离缝宽度接近沉降幅值，如R=4 mm和R=12 mm，离缝宽度分别为3.82 mm和11.83 mm，主要考虑到上部轨道结构的变形能力趋于饱和所致。

4 不同路基变形波长的影响

4.1 变形波长对轨道不平顺的影响

图8为L=10 m和L=20 m条件下，轨道不平顺幅值随路基变形幅值变化的规律曲线。可以得出如下结论。

图8 不同波长条件-轨道不平顺幅值变化规律

(1)路基冻胀及融化回落阶段，轨道不平顺幅值与路基变形幅值具有明显的线性同步关系，且两种波长条件下，轨道不平顺幅值均大于路基变形幅值，与L=5 m时的情况存在明显的差异性。

如D=20 mm时，L=5 m、L=10 m和L=20 m条件下，轨道不平顺幅值分别为17.89，20.18 mm和21.31 mm，再如R=16 mm时，轨道不平顺幅值分别为14.26，16.26 mm和16.99 mm。即表明，同一冻胀或融化幅值条件下，路基变形波长L越大，轨道不平顺幅值越大。

(2)路基沉降阶段，路基变形波长对轨道不平顺幅值存在极大影响。当L=10 m时，轨道不平顺幅值先增大并很快趋于稳定，与L=5 m时的变化规律相似，而当L=20 m时，轨道不平顺幅值随沉降幅值的增大线性增加，表现出明显的差异性。主要是较小的沉降波长条件下，上部轨道结构的变形能力受到极大限制所致。

4.2 变形波长对离缝的影响

图9为L=5 m、L=10 m、L=20 m和L=30 m四种波长条件下，冻胀过程D=20 mm和沉降过程C=16 mm时，底座板与基床表层间的离缝纵向分布。可以得到如下结论。

图9 不同波长条件-离缝纵向分布

(1)路基变形波长L的改变对离缝纵向分布存在明显影响。离缝位置随L的增大向外侧延伸。

(2)冻胀过程中，当L=5 m时，于冻胀峰值处，底座板与基床表层间无离缝，当L≥10 m时，层间存在明显离缝。

(3)离缝宽度随波长L的增大而减小。如D=20 mm时，4种波长条件下的最大离缝宽度分别为10.11，3.81，2.40 mm和1.21 mm，再如，当C=16 mm时，最大离缝宽度分别为15.84，13.66，1.28 mm和0.24 mm。

由此可见，较小的路基变形波长对上部轨道结构与路基间的变形差异影响极大，路基变形波长L的增加，可以明显减小底座板与基床表层间离缝发生的概率。

5 结论

(1)初步揭示了路基冻胀-融化-沉降循环作用下，当路基变形幅值位于伸缩缝时，CRTS I型板式无砟轨道的伤损演化规律与变形特性。

(2)不同波长条件下，轨道板在路基连续性变形过程中均无损伤；底座板损伤萌生于冻胀峰值两侧第一块轨道板板端接缝处，但对应的路基变形波长L较小(L=5 m、L=10 m)；即路基变形波长L增大，轨道结构不易形成塑性损伤。

(3)路基冻胀-融化-沉降循环作用下，L≤10 m时，轨道不平顺幅值先增加后减小，而后反向增加并渐趋平稳；L≥20 m时，轨道不平顺幅值呈先增加后减小，而后反向增加的变化趋势。

(4)塑性损伤形成后，在路基融化回落过程中，钢轨存在部分残余变形，轨道不平顺未完全恢复。

(5)路基变形波长对离缝宽度及纵向分布有极大影响。路基持续变形过程中，底座板与基床表层之间离缝明显，最大离缝宽度随幅值增大而增大。