基于袋装回归树的高铁车体振动耦合因素分析及建模研究

徐 蔚,彭乐乐,钟倩文,郑树彬

(上海工程技术大学城市轨道交通学院, 上海 201620)

车体振动是反映高铁行车安全与乘坐舒适性的关键指标。车体在运行过程中会受轮轨作用力、车辆自身部件的振动、车速等多因素且不同程度的影响[1]。如何获取车体水平、垂直以及侧向振动耦合参数及构建数学模型，排除非相关数据，实现小样本数据的车体三自由度振动监测及分析是目前需要解决的一个难题。

近年来，许多学者针对影响列车车体振动的参数做了相关研究。刘扬[2]利用傅立叶变换，从时频域角度对轮载、轨道不平顺与车体振动加速度三者之间的相关性进行分析；李广军等[3]通过小波变换验证了轨道不平顺是引起列车横向振动的重要因素；李再帏等[4]利用希尔伯特黄变换发现了轨道高低不平顺与列车垂向振动加速度的本征函数存在对应关系。以上研究方法主要是从时、频域波形图定性地分析了轨道参数与列车振动之间的关系，而并未对轨道参数和车体振动的影响程度展开研究。

目前实现车体振动监测的方法主要通过构建动力学模型来获取车体振动加速度。国内外学者们在车辆动力学模型基础上考虑更多的因素，常见的有轨道-车辆耦合模型[5-8]，有考虑更多非线性因素的非线性车轨耦合模型[9]以及风-车-桥系统耦合振动模型[10-11]。但是在影响因素繁多的情况下，车辆动力学模型若考虑的耦合结构越多，会导致建立精确的动力学模型越困难。

同时部分学者展开了利用实测数据以及机器学习的方法实现车体振动监测的研究。耿松[12]利用神经网络建立了轨道不平顺激励下的车辆振动加速度预测模型。但是该方法只考虑了轨道不平顺参数，未考虑车载动力学检测项目[13]对车体振动的影响，导致模型精度较低。徐磊[14]将轨道不平顺时频域统计参数作为输入参数，利用支持向量机分类器实现对车体振动状态的预判。但是该方法未考虑更多的耦合因素，而且仅对车体振动状态进行等级归类，没有定量地实现对列车车体振动加速度的监测。

针对以上研究对耦合因素分析存在定性片面的分析以及车体振动监测模型精度低的问题，提出一种基于袋装回归树的高铁车体振动耦合因素分析及建模方法研究。首先根据GJ-5轨检车给出的检测参数，结合Pearson和Spearman两种相关性算法，定量地分析车体振动耦合因素，排除非相关参数，减少模型样本量。其次，利用得到小样本训练利用袋装集成算法和回归树算法构建的耦合关系模型。最后为验证通过耦合因素分析全面定量地筛选数据并建模的有效性，将模型的输出结果与所有检测参数作为样本集下的模型输出结果以及振动加速度实测值进行对比。

1 耦合因素分析及建模主要流程

图1为系统整体框架，首先结合两种相关性算法定量地提取影响车体振动的耦合因素，并将水平、垂直及侧向车体振动加速度与耦合因素组成3组模型样本集。利用袋装算法对训练样本进行随机抽样，抽取多组子样本来训练相同数量的回归树，将所有回归树模型输出值的平均值作为终值。其次，将拟合度(R-squared)、平均绝对误差(MAE)、均方误差(MSE)、均方根误差(RMSE)作为评价模型性能的指标，同时作为模型耦合参数调整的依据。最后，将得到的3个方向的耦合关系模型性能与所有检测参数训练下的3个耦合关系模型性能进行对比，验证了模型的有效性。

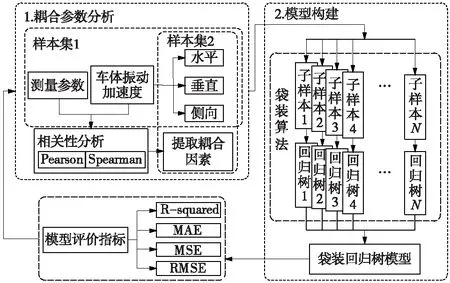
图1 方法流程

2 基于相关性算法的耦合参数分析

获取车体振动耦合参数是解决小样本数据分析的前提。针对参数与车体振动加速度间关联形式的不确定性，结合线性相关算法和非线性相关算法计算相关系数，提取相关性强的耦合参数，得到训练模型的样本集。Pearson线性相关算法[15]公式如下

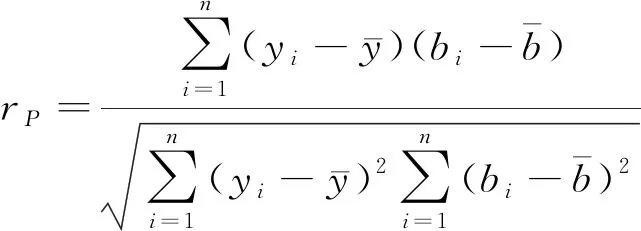
(1)

Spearman算法[16]作为一种非线性相关系数计算方法，计算公式如下

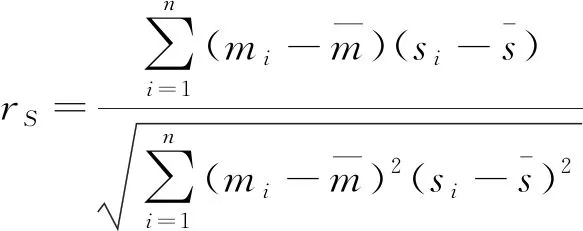
(2)

根据式(1)、式(2)计算出的rP和rS，分别赋予相应的权重p和q，计算出总关联系数。公式如下

rAB=p|rS|+q|rP|

(3)

模型耦合参数的筛选是通过给定总相关系数的阈值ξ实现的。

3 基于袋装回归树的车体振动模型

通过相关性分析剔除了部分非相关参数，将耦合因素与车体振动加速度作为模型训练样本，利用袋装算法将样本集划分成多组子样本集来训练回归树，得到与子样本数量相同的回归树模型，将所有回归树模型进行集成得到袋装回归树耦合关系模型。图2为袋装回归树模型的搭建过程。

图2 袋装回归树模型结构搭建

3.1 回归树数量的确定

袋装算法作为一种集成算法主要用于随机抽取相互独立的训练集，每轮训练并行提高了训练速度[17]。袋装算法的关键问题是训练了多少棵回归树使模型的性能最优，若数量过少则模型的性能就会降低，若过多则会导致计算量过大。因此，可以根据平均绝对误差(MAE)来选择回归树的数量。具体实现方式如图3所示。

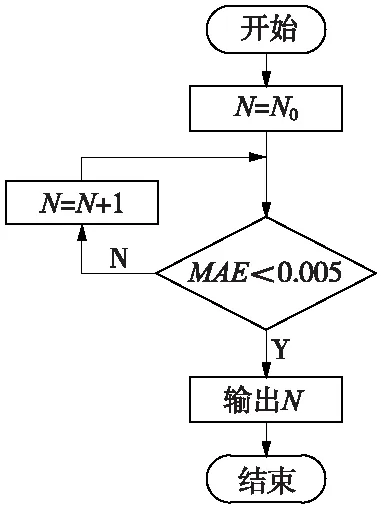
图3 回归树数量确定

设模型样本集为T=(xi，yi)，xi表示耦合因素构成的多维输入量。

(1)先定义回归树模型数量初值为N=N0。

(2)利用自助采样对原始样本进行N0轮抽取得到N0个子样本集，且每个子样本集包含63.2%左右的原始样本。

(3)将得到的子样本集分别训练回归树，重复N0次，得到一系列输出值h1，h2，…，hN。

(4)计算N0棵回归树的输出值均值和平均绝对误差(MAE)。

(5)若MAE>0.05，则N重新取值并按步骤(1)～步骤(4)重新计算结果。直到MAE<0.05时，输出回归树数量N和模型的最终结果。

回归树算法具有对于数据类型差别较大的数据能够准确进行特征选择的优点。回归树的构建主要分为两部分：树的生长和树的剪枝[18]。

3.2 回归树生长

假设将车体振动加速度与耦合因素组成的样本集T=(xi，yi)划分成L个单元，即α1，α2，…，αL。每个单元均有一个振动加速度输出值Cl，回归树模型表示为

(4)

式中，I为指示函数，当x∈αi时I=1，否则为0。

若输入空间已被划分，训练样本数据的预测误差表示为

(5)

当Cl为所有实际车体振动加速度yi的平均值时，平方误差最小。当平方误差最小化时，则可求解每一个单元上的最佳输出值。

回归树通过寻找最优切分变量j和最优切分点s实现输入空间的划分，即求解

(6)

利用选定的最小值对(j，s)划分出的区域和输出值表示为

α1(j，s)={x|x(j)≤s}，α2(j，s)={x|x(j)>s}

(7)

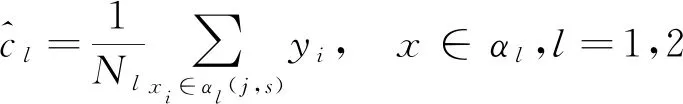
(8)

根据以上步骤可以对区域进行划分，直到节点达到纯度时停止。

3.3 回归树剪枝

原始回归树容易出现“过拟合”现象。为避免这种现象，需要对树进行剪枝。利用K折交叉验证法将子样本集划分为K组，其中K-1作为训练集。先通过训练集使回归树“充分生长”，剩下的一组作为验证集测试回归树的分支规则是否再现。若没有，则认为是过拟合而将该分支修剪。重复上述过程K，使得验证集遍历所有的训练集，平均K次的结果就可以得到单一估值[19]。

3.4 模型性能评价

为衡量模型性能，采用R-Squared、MSE、RMSE以及MAE[20-21]四个指标作为评价标准。公式如下

(9)

(10)

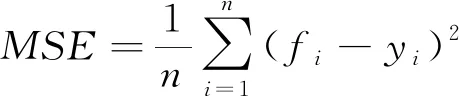
(11)

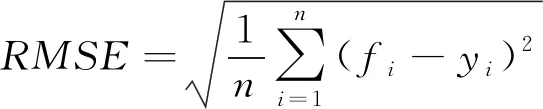
(12)

其中，fi为模型输出的振动加速度值。当R-squared越接近1，拟合程度就越高。当MAE、MSE和RMSE越小时，模型性能越优。

4 实验验证与结果分析

4.1 耦合因素选取

以GJ-5轨检车于2018年8月13日在广深Ⅱ线广州工务段采集的参数作为分析的数据来源。主要选择涉及轨道几何检测项目、车载动力学检测项目41个检测参数用于相关性分析，具体参数内容如表1所示。

表1 用于相关性分析的检测参数

根据给出的各项参数，利用Pearson和Spearman算法分别计算3个方向的车体振动加速度与41个检测参数的线性相关系数和非线性相关系数。根据式(3)取权重p为0.5，q为0.5计算总相关系数。由于列车在运行过程中较平稳，取阈值ξ为0.06，筛选出用于训练模型的耦合因素，结果如表2～表4所示。

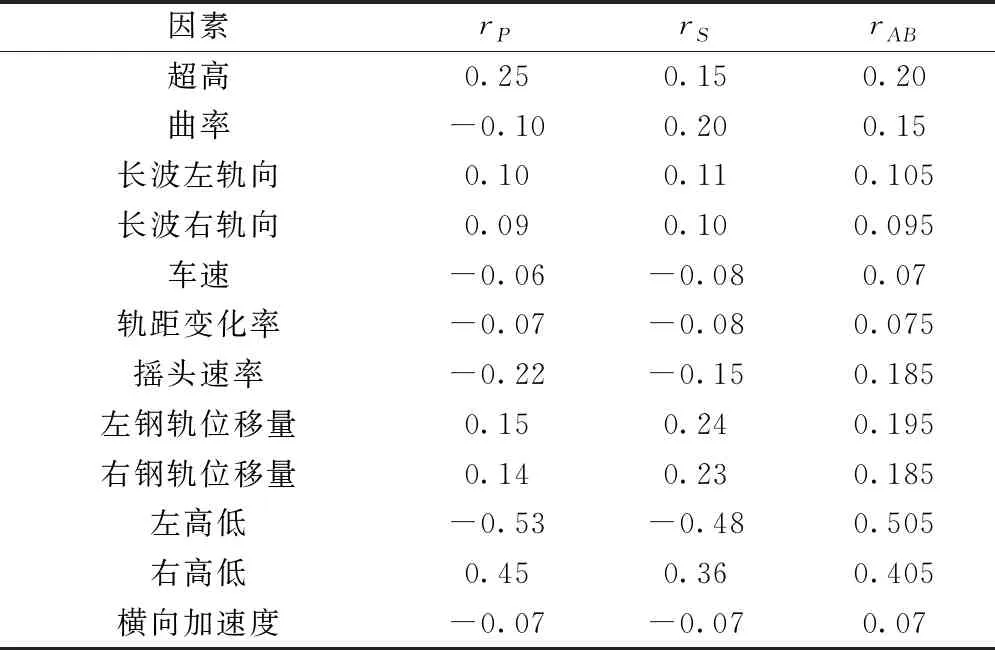
表2 筛选出的水平振动耦合因素

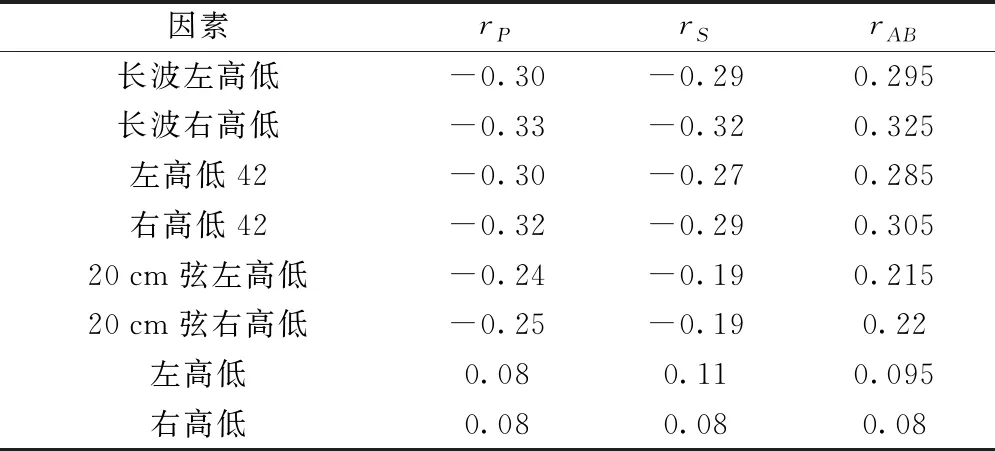
表3 筛选出的垂直振动耦合因素

表4 筛选出的侧向振动耦合因素

从表2～表4可以看出，影响车体水平和侧向振动的耦合因素分别涉及12个参数，影响车体垂直振动的因素有8个。轨道几何检测项目对车体振动的影响较大，轨道高低不平顺是引起车体垂直振动的主要原因。超高、曲率、车速、左右高低以及左右钢轨位移量同时对两种及以上的车体振动状态有影响。

4.2 模型性能分析

通过相关性分析得到模型样本集后，利用袋装集成算法给定回归树学习器数量的初始值N0=40。其次，采用10折交叉验证[22-23]进行树剪枝，以防止过拟合。当MAE<0.05时，水平、垂直以及侧向耦合关系模型中的回归树数量分别是50、60和55。图4～图6给出了车体振动加速度实际值与两种训练样本集下的袋装回归树模型振动加速度输出值的对比曲线。

图4 车体水平振动加速度对比曲线

图5 车体垂直振动加速度对比曲线

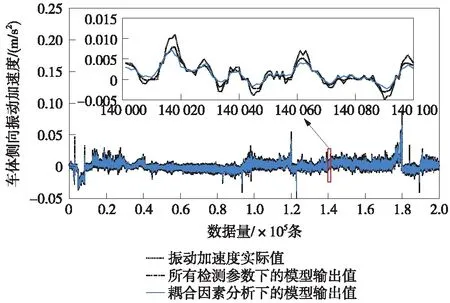
图6 车体侧向振动加速度对比曲线

从图4～图6可以看出两种样本集下建立的袋装回归树模型，其水平、垂直以及侧向振动加速度曲线变化趋势基本吻合，说明了利用相关性算法分析与筛选相关性强的耦合因素的手段是有效的。同时将实际振动加速度曲线与耦合因素分析下建立的袋装回归树模型输出曲线进行比较，可以看出3个方向的模型加速度曲线与实际加速度曲线的变化具有一致性，验证了利用袋装算法和回归树算法建立的耦合关系模型性能较优。

从表5可以看出,水平以及侧向耦合关系模型的R-squared分别是0.88和0.82，该值越接近于1，说明模型的性能越好。垂直方向的耦合关系模型拟合度为0.74，低于水平及侧向的拟合度值，分析原因在于回归树在分裂过程中对差异较大的数据类型能够准确地进行特征提取，而高铁车体垂直振动的耦合因素均是不同波长的超高，参数之间的特征较为相似，影响了回归树的分裂。从误差角度分析，垂直方向的MAE、MSE和RMSE的值均小于0.01，说明该模型能够准确获取车体的振动状态。

表5 耦合因素下的模型性能指标

对比表5和表6可以看出，在两种样本集下的水平、垂向及侧向耦合关系模型的R-squared、MAE、MSE和RMSE四项指标的最大差值为0.06。从误差角度分析，两个垂直方向耦合关系模型的MAE、MSE以及RMSE的最大差值为0.001。在模型精度相当的情况下，样本数据从原先的2460万减小为640万，实现了小样本数据的车体振动测量及分析。

5 结语

针对利用小样本数据准确获取车体振动参数，通过两种相关性算法计算的总相关系数有效地排除了车体振动非相关参数，并且利用袋装回归树算法建立了以车体振动加速度为输出的耦合关系模型。实验表明：在样本量减少74%的情况下模型的精度相当，说明了耦合关系模型可以作为列车车体振动加速度测量模型，用于在小样本下准确地获取车体的三自由度振动加速度，同时减少样本量，提高了模型的训练速度。