逆断层错动作用下地铁隧道结构损伤分析

安韶 ，陶连金 ，边金 ，韩学川 ，吴晓娲

（1.北京工业大学工程抗震与结构诊治北京市重点实验室，北京100124；2.广东海洋大学海洋工程学院，广东湛江524008）

目前，我国很多城市正在进行大规模的地铁建设.但如北京、乌鲁木齐、天津及太原等城市位于高烈度区且存在多条活动断裂带，由于地铁工程走向往往取决于城市交通功能的需求，避让原则[1]常常无法实现.穿越活动断裂带的隧道在断层错动作用下会发生严重破坏，如5.12 汶川地震白云顶隧道距映秀端洞口60 m 处二衬错台近40 cm，隧道破坏长20 m，局部发生垮塌，路面破损、开裂起拱[2].因此研究断层错动作用对城市地铁隧道结构的影响，是保障隧道工程安全的关键性课题之一.

跨断层隧道结构的影响研究方法包括震后调查、数值模拟及模型试验法，其中震后调查受诸多条件限制，难以大规模开展，因此主要采用后两种方法.在模型试验方面，Kontogianni 等[3]通过模型试验研究了在不同断层倾角的逆断层、走滑断层作用下隧道衬砌管片环向接头部位应力应变规律.Lin 等[4]通过提升底板试验模拟了逆冲断层作用下砂土中盾构隧道变形破坏特点.陈俊岭等[5]通过振动台试验研究了近断层滑冲效应下风力发电塔动力响应，结果表明近断层地震滑冲效应脉冲使得结构响应明显增大.刘学增等[6]通过模型试验研究了断层倾角为75°的逆断层错动下公路隧道衬砌的反应规律，给出了受拉受压区间以及最大拉压应变发生的位置.黄强兵等[7]通过地裂缝活动模型试验，研究了西安地铁2号线隧道正交穿越地裂缝带的设防参数.胡辉[8]进行了相似模型试验，研究了跨断层隧道变形缝设置的有效性.孙风伯等[9]等推导了隧道最大节段长度并通过实验得以验证.王明年，崔光耀等[10]展开了断裂黏滑错动作用下模型试验并研究了减震缝与减震层的减震效果，为实际隧道工程的建设提供了参考和依据.在数值模拟方面，Mohammad 等[11]通过数值模拟研究了逆断层错动作用下距错动处不同位置的隧道附近土层剪切带出现的位置及传播路线.王琼[12]采用有限元方法研究了断层错动对长大山岭隧道的非线性反应，得到了应力屈服破坏顺序、屈服范围和产生高应力区的位置.张维庆[13]采用数值模拟研究了穿越断层隧道在断层错动和地震力分别作用下的震害机理.赵颖等[14]采用数值模拟研究了走滑断层位错作用下城市地铁隧道衬砌结构的损伤发展，重点分析了结构损伤的开始部位、发展过程以及最终的损伤程度，并建立了能够估计结构损伤范围及破坏最严重位置的统计关系式.Shahidi 等[15]针对伊朗Koohrang-III 输水隧道跨活动断裂的情况，提出断层带部分衬砌采用铰接设计方法，并计算确定了适宜的衬砌节段长度和柔性连接宽度.赵坤等[16]采用有限元法通过正交试验研究了衬砌节段长度、柔性连接宽度、柔性连接材料强度3 种因素对衬砌结构内力的影响.刘国庆等[17]对跨断层水工隧洞建立三维有限元模型，考虑动接触后在地震作用下围岩出现了明显的错动位移，断层破碎带的存在造成了衬砌位移和应力的增加.

以上研究成果对于穿越活动断层的隧道工程均具有一定的指导意义，但仍然存在一些不足.目前的研究对象主要集中在深埋山岭隧道，对城市浅埋地铁隧道研究较少，且受条件所限，现有模型试验尺寸都比较小，缺乏对隧道纵向尺度方向的考虑；数值模拟试验结构大多采用弹性本构，结构塑性损伤分析方面研究较少.

本文以乌鲁木齐地铁2 号线隧道穿越西山断裂带工程为依托，考虑活动断层错动作用下土层与隧道结构的相互作用，采用ABAQUS 建立三维有限元弹塑性模型，研究了隧道二次衬砌塑性应变发展过程、拉压损伤因子及剪切应变的分布，给出了隧道拉裂严重受损、轻微受损及无受损的区间范围，分析了不同错动位移、隧道底部距围岩交界面不同垂直距离时隧道及不同断层破碎带宽度的损伤破坏规律，进行了设置柔性接头的减灾效果研究，以期为实际工程提供参考.

1 工程背景

乌鲁木齐轨道交通2 号线马料地站-平川路站区间，由西外环的马料地站起，沿马料地街向西，再向北转到平川路北园春市场平川路站，中间段穿越西山断层，全长约873.1 m.拟建区间底板埋深17.6～26.5 m，标高831～842.6 m，地质剖面简图见图1.西山断层形成于中更新世中晚期，最新活动时间为晚更新世晚期，属晚更新世活动断层，走向N45°-75°E，倾向 N，倾角 44°～83°，具逆冲性质.穿越断层段前后200 m 范围内隧道区间拟采用矿山法施工，其余地段拟采用盾构法施工.根据乌鲁木齐轨道交通2号线详勘报告，考虑未来100 年有突发事件的可能性，建议设防垂直位错hv=0.165 m.

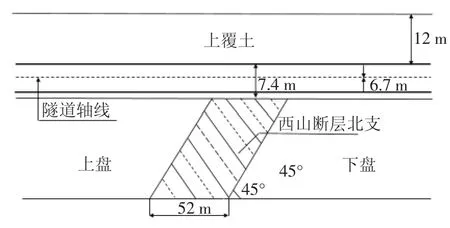
图1 地质剖面简图Fig.1 Sketch of geological profile

2 模型建立及参数选取

取断层破碎带前后各100 m 范围内建立计算模型，模型长×宽×高为252 m×68 m×60 m，隧道埋深为12 m，断层倾角为45°，隧道直径为6.7 m，模型网格划分见图2，隧道结构采用复合式衬砌，纵向划分126 份网格，网格纵向间距为2 m.土体假设为理想弹塑性材料，采用摩尔库伦屈服准则，各土层参数见表1，衬砌结构采用ABAQUS 中的塑性损伤模型，依据标准GB 50010—2010《混凝土结构设计规范》[18]的规定，定义衬砌混凝土弹塑性应力应变关系，初期支护与二次衬砌结构参数见表2.初期支护厚0.35 m，混凝土强度等级为C45；二次衬砌厚0.25 m，混凝土强度等级为C50.考虑隧道与土体之间的摩擦，其接触面设置罚摩擦，摩擦系数取为0.4[19].模拟分析分为三步：初始地应力平衡-隧道开挖-施加断层位移，在前两个步骤中，模型底部及侧边界施加法向约束，上部边界为自由边界，在最后一个步骤中，由于逆断层错动为上盘相对下盘作向上运动，因此为实现逆断层错动过程，释放上盘底部及侧边界法向约束，并在相应的位置上施加位移荷载以模拟断层错动，位移加载边界条件见图3.

图2 土层-隧道模型网格Fig.2 Meshing of soil-tunnel model

表1 土层物理力学参数Tab.1 Physical and mechanical parameters of soil layers

表2 结构物理力学参数Tab.2 Physical and mechanical parameters of tunnel structure

图3 断层错动加载边界Fig.3 Boundary of fault dislocation

3 结构破坏分析

3.1 位移分析

施加断层错动位移16.5 cm，图4 为二次衬砌竖向位移沿隧道纵向距离的分布曲线.图4 中，以模型上盘边界处为0 点，往右侧指向下盘方向为正，破碎带两侧边界分别在纵向坐标100 m 和152 m 处，断层错动发生在纵向坐标100 m 处，纵坐标的竖向位移，以竖直向上为正，向下为负.由图4 可知，断层错动发生后，隧道衬砌沿着纵向发生了“S”状弯曲，上盘受竖向位移的作用，二次衬砌产生向上的位移16.5 cm，随着纵向距离的增加，二次衬砌竖向位移逐渐减小.

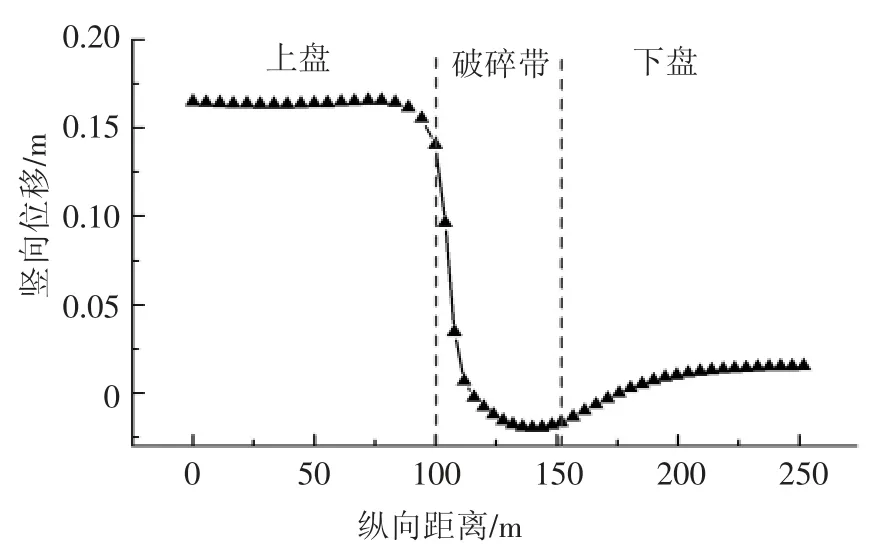
图4 二次衬砌竖向位移纵向分布曲线Fig.4 Longitudinal distribution curve of vertical displacement of secondary lining

3.2 塑性应变发展过程

图5 为断层错动位移过程中二次衬砌的塑性应变发展过程.由图5 可知，当断层位移不大于3 cm时，二次衬砌未发生塑性应变，代表结构材料尚未屈服.当断层位移逐渐增大时，最大塑性应变首先出现在上盘拱顶，然后出现在上盘拱底，最后出现在破碎带内拱腰处并在此逐渐累积.产生这种现象的可能原因是由于隧道埋置在上覆土层内，隧道底部最早与土体共同运动，隧道顶部受到覆土压力与底部位移的共同作用，最早产生塑性应变.当隧道顶部与上覆土层之间的作用逐渐达到稳定时，隧道底部开始与土体产生相互作用，塑性应变在隧道底部逐渐增大，隧道横截面逐渐变为椭圆面，随着断层位移的进一步增大，椭圆面拱腰处产生应力集中，塑性应变在拱腰处逐渐累积直至破坏.

图5 塑性应变发展过程Fig.5 Development process of plastic strain

3.3 拉压损伤因子分布

图6 为二次衬砌纵向受压受拉损伤因子分布云图，图7 和图8 为二次衬砌拱顶、拱腰及拱底的受压受拉纵向分布曲线图.由图7 和图8 可知，最大受压受拉损伤因子出现在破碎带拱腰处，上盘内拱顶处受拉，拱底处受压，在受损最为严重的拱腰处指向下盘方向的破碎带内拱顶处受压，拱底处受拉.由以上分析可知，二次衬砌拱腰处拉压破坏最为严重，拉压损伤因子沿纵向均呈“S”型分布，与衬砌变形一致.

图6 受压受拉损伤因子分布云图Fig.6 Distribution cloud of compressive and tensile damage factor

图7 隧道拱顶、拱腰及拱底受压损伤因子纵向分布曲线Fig.7 Longitudinal distribution curve of compressive damage factor of tunnel vault，waist and invert

图8 隧道拱顶、拱腰及拱底受拉损伤因子纵向分布曲线Fig.8 Longitudinal distribution curve of tensile damage factor of tunnel vault，waist and invert

3.4 剪应变

图9 为二次衬砌剪应变分布云图.由图9 可知，最大剪应变发生在拱腰处.图10 为拱腰处剪应变（绝对值）纵向分布曲线图，拱腰处最大剪应变发生在纵向坐标105 m 处，最大值为0.019 3.混凝土抗剪强度和抗压强度之比约为0.095～0.121[20]，依据Zia的建议，混凝土的剪切模量为其弹性模量的40%[21].由此可求得C50 混凝土允许的极限剪切应变εs：

拱腰处剪应变为1.93e-2，远大于极限剪切应变，表示混凝土极可能发生了严重的剪切破坏.

图9 二次衬砌剪应变分布云图Fig.9 Distribution cloud of shear strain of secondary lining

图10 拱腰处剪应变纵向分布曲线Fig.10 Longitudinal distribution curve of shear strain of tunnel waist

3.5 结构拉裂受损区间划分

由3.3 和3.4 节隧道的受拉、受压与剪切破坏分析可知在断层破裂面附近，二次衬砌受到拉压和剪切的共同作用，距破裂面较远范围内，上盘隧道拱顶处、破碎带内拱底处主要承受拉力，上盘拱底处、破碎带内拱顶处主要承受压力.二次衬砌破坏形式的纵向分布示意图见图11.

图11 二次衬砌破坏形式纵向分布示意图Fig.11 Schematic diagram of the damage form along the tunnel axis of secondary lining

为进一步区别隧道的拉裂严重受损区、轻微受损区与无受损区，本文以受拉损伤因子计算得到混凝土的裂缝宽度进行划分.Chen 等人[22]提出了一种通过拉伸损伤因子dt合理计算混凝土裂缝的计算公式：

式中：hc为特征值长度，对于八节点积分单元而言等于单元边长[23]；σt为拉应力；E0为初始弹性模量.

由公式（2）得到当混凝土裂缝宽度为0.2 mm时，受拉损伤因子为0.838.依据《水工混凝土结构设计规范》[24]，表3 给出了混凝土裂缝宽度和受拉损伤因子定义的二次衬砌（C50）受损程度区间划分依据.

表3 二次衬砌受损程度划分Tab.3 Classification of damage degree of secondary lining

结合图8 隧道二次衬砌拱顶、拱腰及拱底的受拉损伤因子纵向分布曲线，得到二次衬砌沿纵向拉裂受损区间分布见图12.

图12 二次衬砌拉裂受损区间纵向分布Fig.12 Longitudinal distribution of tensile-crack damaged interval of secondary lining

由图12 可知，二次衬砌拉裂严重受损区集中在破碎带内，发生在纵向区间105 m 至115 m 共10 m范围内，轻微受损区发生在严重受损区两侧，沿破碎带指向上盘方向为16 m，指向下盘方向为14 m，总长为30 m.

4 影响因素分析

考虑到错动危险的不确定性、施工时隧道埋深位置的选取以及断层破碎带宽度的不同，本文重点分析了不同断层竖向错动位移hv、隧道底部距围岩交界面不同垂直距离b 及不同断层破碎带宽度的二次衬砌结构的破坏损伤规律，依此建立模拟工况见表4.

表4 不同影响因素模拟工况Tab.4 Simulated working conditions with different influencing factors

4.1 不同断层错动量影响分析

表5 为不同错动位移下的最大塑性应变，图13为拱腰处剪应变纵向分布曲线图，最大塑性应变及最大剪应变均出现在拱腰处.由图表可知，当错动位移逐渐增大时，塑性应变和剪应变均增大.

表5 不同错动位移下的塑性应变Tab.5 Plastic strain under different dislocation displacements

当错动位移分别为10 cm、16.5 cm 和20 cm 时，受压和受拉损伤因子最大值均出现在破碎带内拱腰处，图14 和图15 为隧道沿纵向各个横截面上最大受压和受拉损伤因子的纵向分布曲线图，由图可知，当错动位移逐渐增大时，隧道拉压损伤因子越大，代表二次衬砌受拉受压破坏越严重.

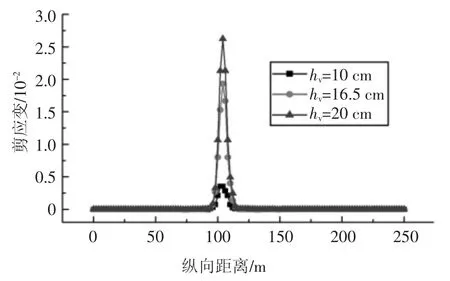
图13 不同错动位移下的拱腰处剪应变Fig.13 Shear strain of tunnel waist under different dislocation displacements

图14 最大受压损伤因子纵向分布曲线Fig.14 Longitudinal distribution curve of maximum compressive damage factor

图15 最大受拉损伤因子纵向分布曲线Fig.15 Longitudinal distribution curve of maximum tensile damage factor

4.2 隧道底部距围岩交界面不同垂直距离影响分析

表6 为隧道底部距围岩交界面不同垂直距离的最大塑性应变，图16 为拱腰处剪应变纵向分布曲线图，最大塑性应变及最大剪应变均出现在拱腰处.由图表可知，当垂直距离逐渐增大时，塑性应变和剪应变均减小，当垂直距离等于4.7 m 时，塑性应变为0，剪应变接近于0.

图16 不同隧道底部距围岩交界面垂直距离的拱腰处剪应变Fig.16 Shear strain of tunnel waist under different vertical distances from tunnel bottom to the interface of surrounding rocks

图17 和图18 为隧道底部距围岩交界面不同垂直距离的隧道横截面最大受压和受拉损伤因子的纵向分布曲线.由图可知，当隧道底部距围岩交界面的垂直距离为0.7 m 时，受压和受拉损伤因子最大，且最大值出现在破碎带内拱腰处；当隧道底部距围岩交界面的垂直距离为2.7 m 时，受压损伤因子最大值出现在上盘拱底处，受拉损伤因子出现在隧道上盘拱顶处；当隧道底部距围岩交界面的垂直距离为4.7 m 时，受压受拉损伤因子最小均为0.结合以上剪应变和塑性应变的分析可知，当隧道底部距围岩交界面的垂直距离逐渐增加时，隧道遭受的破坏越严重，当隧道底部距围岩交界面的垂直距离为4.7 m 时，隧道未发生破坏，这主要是因为距离越大，土层越厚，在错动位移传播过程中耗散掉了大部分能量.

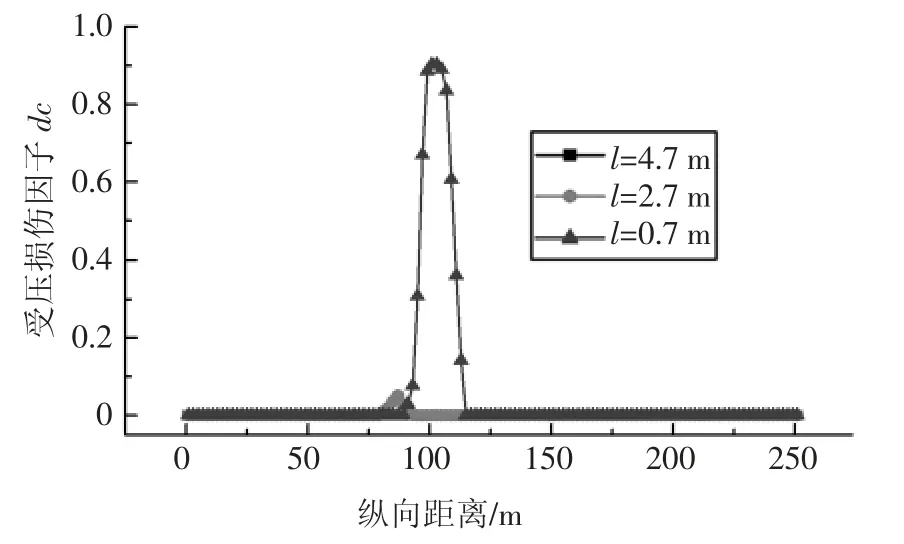
图17 最大受压损伤因子纵向分布曲线Fig.17 Longitudinal distribution curve of maximum compressive damage factor

图18 最大受拉损伤因子纵向分布曲线Fig.18 Longitudinal distribution curve of maximum tensile damage factor

4.3 不同断层破碎带宽度影响分析

表7 为不同破碎带宽度下的最大塑性应变，图19 为拱腰处剪应变纵向分布曲线图，破碎带宽度为2 m 时，最大塑性应变出现在拱底处，破碎带宽度为26 m 和52 m 时，最大塑性应变出现在拱腰处.不同破碎带宽度最大剪应变均出现在拱腰处，分别为3.804 02e-4、0.014 25 及 0.015 31.由图表可知，当破碎带宽度由2 m 变为26 m 时，最大塑性应变增加了4 952.04%，最大剪应变增加了3 646.05%；当破碎带宽度由26 m 变为52 m 时，最大塑性应变增加了5.55%，最大剪应变增加了7.44%.

表7 不同破碎带宽度的塑性应变Tab.7 Plastic strain under different widths of fracture zone

图19 不同破碎带宽度的拱腰处剪应变Fig.19 Shear strain of tunnel waist under widths of fracture zone

图20 和图21 为隧道沿纵向各个横截面上最大受压和受拉损伤因子的纵向分布曲线图.当破碎带宽度分别为2 m、26 m 和52 m 时，最大受压损伤因子分别为0.159 43、0.866 27 及0.901 48，最大受拉损伤因子分别为0.902 12、0.933 2 及0.954 3.由图可知，当破碎带宽度由2 m 变为26 m 时，最大受压损伤因子增加了443.35%，最大受拉损伤因子增加了3.45%；当破碎带宽度由26 m 变为52 m 时，最大受压损伤因子增加了4.06%，最大受拉损伤因子增加了2.26%.结合以上分析可知，当断层破碎带宽度由2 m 变为26 m 时，隧道衬砌破坏显著增加，当破碎带宽度由26 m 变为52 m 时，衬砌破坏会出现很小程度的增加，基本保持稳定.产生这种现象的原因依据是泥岩与煤层为Ⅴ级围岩，粉质黏土与圆砾为Ⅵ级围岩，断层错动位置发生在泥岩与煤层接触面处，当破碎带（煤层）宽度较小时，下盘内的粉质黏土发挥主要作用，其围岩性质较软，有利于隧道的变形，衬砌破坏较轻.随着破碎带宽度的逐渐增加，破碎带围岩对隧道的影响越来越大，二次衬砌破坏逐渐增加，当破碎带宽度达到26 m 时，破碎带围岩对隧道的影响基本保持稳定.

图20 最大受压损伤因子纵向分布曲线Fig.20 Longitudinal distribution curve of maximum compressive damage factor

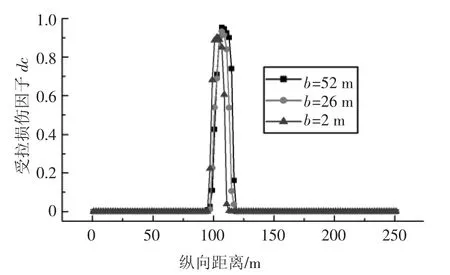
图21 最大受拉损伤因子纵向分布曲线Fig.21 Longitudinal distribution curve of maximum tensile damage factor

5 柔性接头减灾效果研究

断层错动会对地下结构造成严重的破坏，因此研究有效的抗断设计方法十分必要且具实际意义.目前常用的抗断减灾设计方法主要包括超挖设计、柔性接头、设置减震层及注浆加固4 种，该工程采用设置柔性接头的方法.为确定衬砌节段长度，在设防错动位移作用下二次衬砌的弯矩纵向分布见图22，如图所示，在错动面两侧32 m 处隧道二次衬砌形成反弯点，依据Shahidi[15]等人的研究，衬砌节段长度最大不应大于32 m，考虑到混凝土台车的宽度一般为6 ～12 m，同时考虑到防水要求，衬砌节段长度不宜设置太短，因此节段衬砌长度最终确定为12 m，设置范围分布在断层破碎带及其附近共96 m，柔性接头长度0.15 m，按不利工况考虑，假定断层错动的位置发生在节段衬砌中点处，模拟中柔性接头被简化为理想弹性材料，密度为1 000 kg/m3，弹性模量为7.8 MPa，泊松比0.47，柔性接头设置示意图见图23.

图22 弯矩纵向分布曲线Fig.22 Variations of computed bending moment along longitudinal direction

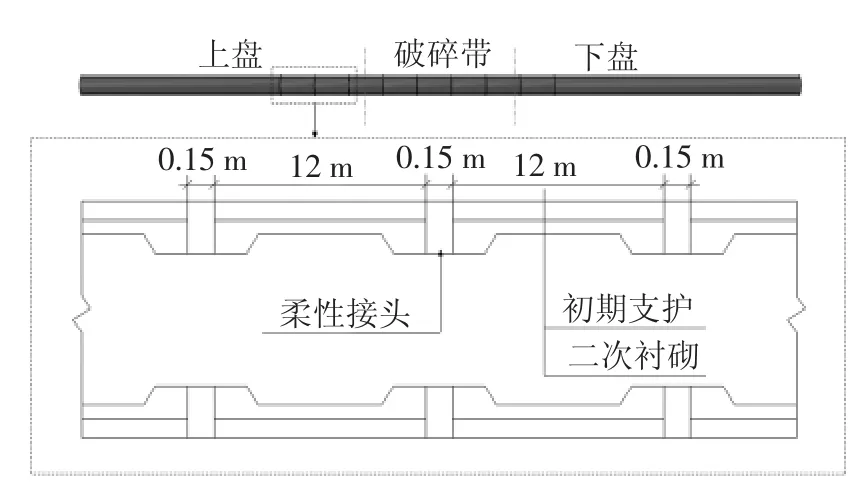
图23 柔性接头设置示意图Fig.23 Sketch diagram of flexible joints

施加断层错动位移16.5 cm，二次衬砌的塑性应变、拉压损伤因子及剪应变云图见图24.对比第3 节相应的分析可知，二次衬砌塑性应变降低了97.8%，最大受压损伤因子降低了90.7%，最大受拉损伤因子降低了88.8%，最大剪应变降低了98.5%.值得注意的是，设置柔性接头以后，二次衬砌发生破坏的位置主要集中在跨断层错动面附近的柔性接头处，因此应对此处的结构进行重点加固.综合以上分析可知，设置柔性接头可以显著降低断层错动变形对结构的损害，但由于柔性接头弹性模量低，较为“柔软”，因此成为了抗断薄弱部位，结构损伤最大的位置也往往出现在柔性接头附近.以上分析体现出了跨断层地下结构的“以适应地层变形为主，局部结构加固为辅”的设计理念.

6 结 论

1）逆断层错动作用下，错动位移不大于3 cm时，二次衬砌塑性应变为0，结构未发生破坏.当错动位移进一步加大时，塑性应变首先出现在拱顶，然后是拱底，最后在拱腰处累积.当错动位移达到16.5 cm 时，错动面及其附近的拱腰处产生拉压剪的共同破坏，远离破裂面上盘内拱顶处受拉，拱底处受压，在受损最为严重的拱腰处指向下盘方向的破碎带内拱顶处受压，拱底处受拉.

2）基于拉伸损伤因子计算得到了二次衬砌的混凝土裂缝宽度，并依此为依据将隧道二次衬砌受损区间划分为拉裂严重受损区、轻微受损区与无受损区.其中，拉裂严重受损区集中在破碎带内，发生在纵向区间105 m 至115 m 处，总长共10 m；轻微受损区出现在严重受损区两侧，沿破碎带指向上盘为16 m，指向下盘为14 m，总长为30 m.

3）断层错动位移越大，结构受损越严重.隧道底部距围岩交界面垂直距离越大，土层越厚，错动位移传播过程中消耗能量越多，结构受损越轻.断层破碎带宽度越大，隧道破坏越严重，当破碎带宽度达到一定值时，破碎带对隧道的影响基本保持稳定.

4）节段衬砌之间设置柔性接头可以显著降低错动位移对结构的危害.但由于柔性接头较为柔软，是抗断薄弱部位，设置柔性接头以后受损最为严重的区域往往出现在变形缝及其附近，因此应对该处结构进行重点加固.