大型多指廊屋盖风荷载非高斯特性风洞试验研究

闫渤文 ，赵乐 ，刘堃 ，2，李正良 ，周绪红 ，3

（1.重庆大学山地城镇建设与新技术教育部重点实验室，土木工程学院，重庆400045；2.中国电力工程顾问集团中南电力设计院有限公司，湖北武汉430000；3.湖南大学土木工程学院，湖南长沙 410082）

大型屋盖结构因造型美观、新颖多变，且结构自重较轻、跨度大等优势被广泛用于机场、体育馆等大型公共建筑.由于大型公共建筑自身的功能需求和艺术造型的独特性，每个建筑结构选型和建筑外观差别较大，风荷载设计可互相借鉴资料较少，并且此类结构具有跨度大、自重轻、结构轻柔以及阻尼小等特点，从而大大增强了其对风荷载的敏感度.因此，风荷载通常是在大型屋盖结构设计中起到主要控制作用.由于大型屋盖风荷载作用的复杂性和三维特性，基于缩尺模型的风洞试验研究是确定大型空间结构设计风荷载的主要依据.

目前针对具有典型形体（球面、柱面、鞍形和悬挑等）的大型空间结构屋面风荷载，国内外已经开展了许多风洞试验[1-7]，并得到这几种典型形体屋盖几何形状与风压分布之间的变化规律，为这类结构的抗风设计和结构气动外形优化都提供了非常重要的指导和建议[8].但在实际工程中，大型屋盖结构的外形通常更为复杂，其风荷载分布特征明显不同于典型形体的屋面风荷载特征，特别是近年来多指廊屋盖结构被广泛地应用于机场航站楼等大型公共建筑中，因此亟需开展风洞试验对其风荷载分布特征进行研究.另一方面，大型多指廊屋盖转角多、指廊狭长、迎风屋檐宽度大，形状复杂多变.在这些转角、坡度以及弧度较大等区域，气流分离再附现象严重，且容易形成三角涡、柱形涡等，屋盖主要受分离的旋涡作用，主要适用于无明显分离的自由剪切湍流的准定常理论失效，中心极限定理也不再适用[9].此时屋盖风压表现出较强的非高斯性，风压时程分布不再有对称性且具有较强的随机脉冲信号，出现明显的负向毛刺[5].在风压脉冲作用下，屋面容易受到瞬时强力作用，容易导致局部结构破坏.因此，对风压非高斯特性的研究不仅可以更好地发现风压分布特征，也可以为屋盖结构抗风设计提供更加精确可靠的依据.在大型屋盖非高斯风压分布方面，有研究者也开展了一些工作，如孙瑛等[9]探讨了大型平屋盖非高斯风压分布的原因，并结合第三、四阶统计量，给出了划分高斯与非高斯区域的标准.叶继红等[10]结合5 种典型形式的大型盖风洞试验，分别采用了统计方法和基于K-S 检验的曲线拟合方法对屋盖进行了高斯与非高斯分区.上述非高斯特性的研究只针对于一些比较理想的屋盖模型，对于实际比较复杂的大型多指廊屋盖，非高斯风压分布研究还比较少

见[11-12].

对于大型多指廊分离式结构，由于各分肢弧度大、顺风深度窄，转角多以及屋盖间和各指廊间的风压干扰，风荷载特性更加复杂，有必要针对这一特殊形式展开风洞试验研究.本文基于我国大型机场航站楼（指廊间最大距离约1 500 m），开展了系统的刚性测压风洞试验研究，对大型多指廊屋盖的表面风压分布规律进行了阐述，着重分析了航站楼的重点部位如各分肢外挑屋檐、转角处的风压分布特征，最后基于风压的统计特性，对整体大型多指廊屋盖进行了高斯与非高斯分区.

1 试验概况

1.1 试验模型

本文研究的大型多指廊屋盖由A、B、C、D 四部分组成，A、C 最大投影尺寸440 m×109 m，最高点标高约 25 m；B 指廊最大平面尺寸 257 m × 114 m，屋面最高点高度约29 m；D 区中央大厅最大平面尺寸511 m×284 m，最高点标高约45 m.其中指廊间最大距离约为1 500 m，为我国大型机场航站楼，整体结构造型新颖，屋盖跨度大，体型复杂，如图1 所示.该航站楼试验模型缩尺比为1 ∶100，最大阻塞比约为5%，试验模型为刚性模型，采用质量轻，强度高，高温下可塑性好的ABS 板制成，共分为3 层，如图2所示，此时风向角为0°，周边建筑较为规则，采用三合木板制作，其布置示意图如图3 所示.

图1 大型多指廊屋盖机场航站楼效果图Fig.1 Architecture drawings of the airport terminal

图2 试验模型照片Fig.2 Photos of the wind tunnel test

由于结构的对称性，模型测点位置分布按照不小于100 m2/个的原则进行单侧布点，总共布置了4 234 个测点，其中1 层测点908 个，2 层测点1 396个，3 层测点320.测点主要分布在模型表面，包括屋盖、围护幕墙、上下悬挑等部分.典型测点的布置图如图4 所示.

图3 周边建筑布置示意图Fig.3 Diagram with surrounding buildings

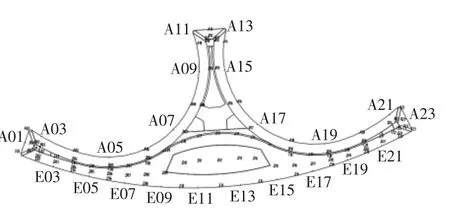
图4 典型测点空间分布图Fig.4 Spatial distribution of representative pressure taps

1.2 风洞及测量设备

风洞试验在湖南大学风工程试验中心HD-2 大气边界层风洞的第三试验段完成.第三试验段为开口型断面，试验段横截面尺寸为15 m（长）×8.5 m（宽）×2.0 m（高），最大风速可达18 m/s.由于模型尺寸较大，本试验加工了直径8 m、厚度8 mm 的木制转盘，并对边缘进行15°倒角，用于模型转动.风洞试验中来流条件依据《建筑结构荷载规范》GB 50009—2012[13]中B 类地貌条件（地面粗糙度α=0.15）进行模拟，通过改变尖劈和粗糙元被动模拟平均风速剖面、湍流度特性及风功率谱等大气边界层风场特性，如图5 所示.

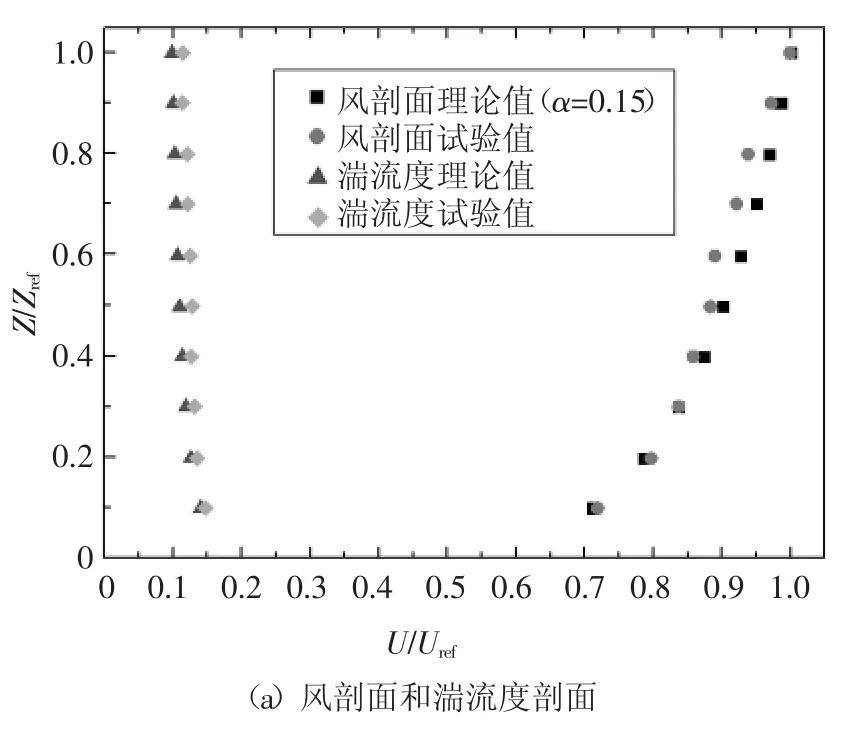
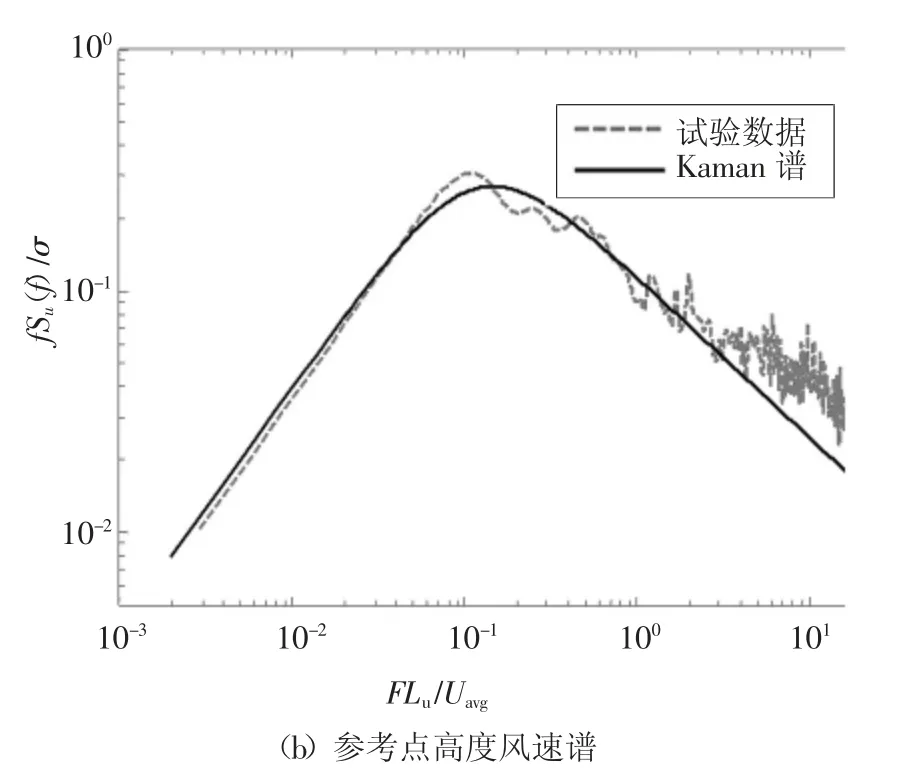
图5 风洞试验风剖面、湍流度剖面及参考点高度处风速谱Fig.5 Profiles of wind speed，turbulence intensity and wind velocity power spectrum at the reference height in the wind tunnel test

表面压力测量采用DSM3400 电子式压力扫描阀系统和信号采集及数据处理模块，采样频率为330 Hz，采样时长为30 s，采样样本长度为9 900，为确保试验数据的稳定性，共采样3 次.

1.3 试验工况及数据处理

本试验共设定了24 个工况，每15°风向角为一个工况，如图6 所示.

本文以梯度风高度为参考高度，压力系数计算方法如下[14].

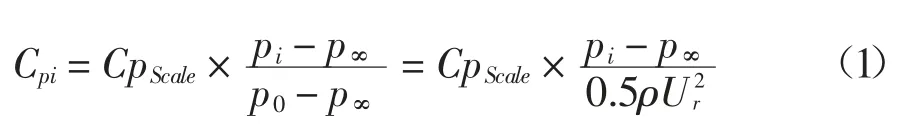
式中：Cpi和pi分别表示测点i 处的压力系数和压力（Pa），p0和p∞分别表示试验参考高度处的总压和静压（Pa），ρ 是空气密度（kg/m3），Ur是参考高度风速（m/s）.CpScale为以梯度风为参考风压对试验风压系数换算的因子，本文取CpScale=0.557 8.

脉动风压均方根Cprms通过式（2）求得：

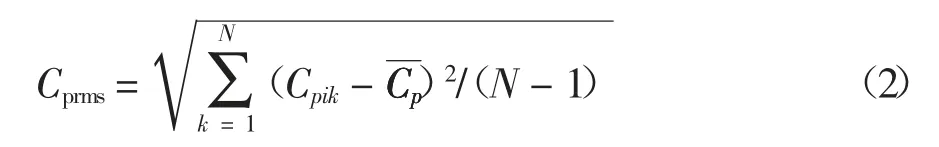
式中：Cpik表示第i 个测压孔风压系数时程，N 表示样本数，k 表示其中的某一个样本.

2 风压非高斯性判别方法

常用的风压非高斯性判别方法包括高阶统计量方法，K-P 检验法或K-S 检验法进行非高斯分区.本文采用高阶统计量方法和K-S 检验法分别对该大型多指廊屋盖进行非高斯分区.

2.1 高阶统计量方法

根据以往的研究发现高阶统计量偏度（Skew ness）和峰度（Kurtosis）可以作为划分高斯和非高斯过程的标准，通常依据实际的风压分布特性，划分偏度峰度范围，作为高斯和非高斯分区的界限.根据叶继红等[10]确定偏度峰度范围的标准，即满足偏度和峰度整体变化趋势不偏离和在自身变化范围内置信概率一致，分别计算所有测点在4 个典型风向角下的累积概率密度，如表1 所示.

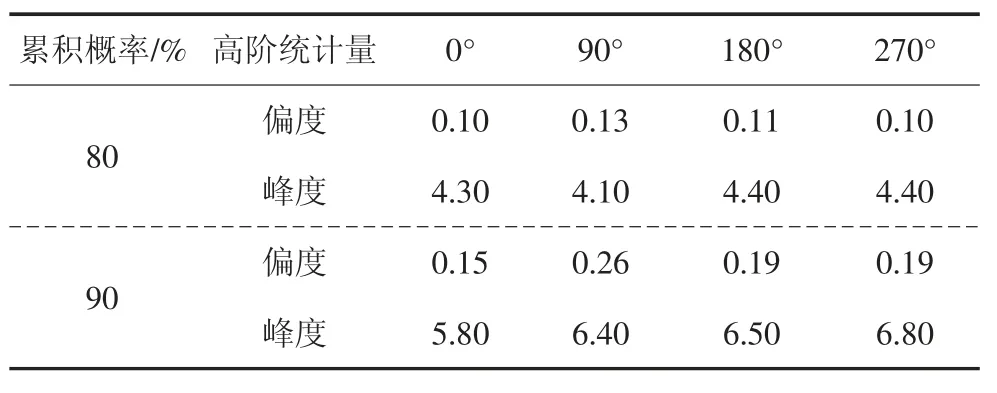
表1 不同累积概率下偏度峰度Tab.1 Skewness and kurtosis of different CDF

通过对试验数据的分析可知，峰度偏度存在一定关系，本文用归一化峰度（（K-S）/K）表示，如图7所示.

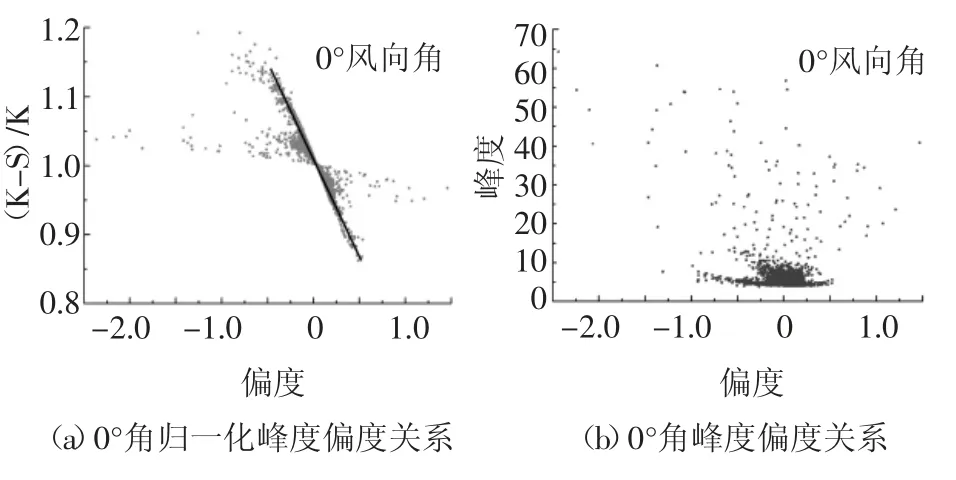
图7 偏度和峰度及其归一化值关系图Fig.7 Relationship between skewness and kurtosis and normalized kurtosis

2.2 柯尔莫哥洛夫-斯米尔诺夫检验方法原理

假设检验是以样本的信息推断总体的假设，对其正确性进行判断.其主要推断方法是反证法，即原假设成立记为H0，若从样本所发生的概率推断吻合原假设，结果接受原假设.若样本发生是小概率事件，结果拒绝原假设.这种“小概率”值称为显著性水平，记为α，假设检验的判断与α 密切相关.假设检验分为参数检验和非参数检验，非参数检验是用来判断一个总体的分布是否吻合事先假定的分布类型；用来判断一个总体分布是否符合高斯分布的检验称为高斯性检验，本文采用的是非参数检验[15].

Kolmogorov-Smirnov（Dn）检验法

这种检验方法不需要考虑划分区间上Fn（x）与假设分布F0（x）偏差，而是考虑每点的偏差.根据Glivenko-Cantelli[16]定理，在n 充分大时，样本经验分布函数Fn（x）很好的近似于总体分布F（x），二者偏差一般不会出现较大值.于是用二者偏差值得最大值构造一个统计量：

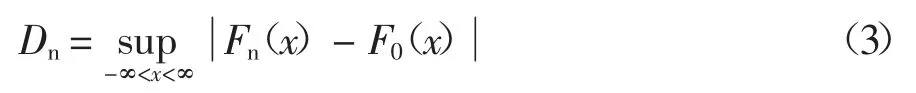
H0：F（x）=F0（x）为真，Dn的值一般较小（n 充分大），若Dn值较大则拒绝H0.于是对于显著性水平α，得到：

设总体的分布函数 F（x）连续，（ξ1，ξ2，…，ξn）为 ξ的样本，当H0：F（x）=F0（x）为真时：

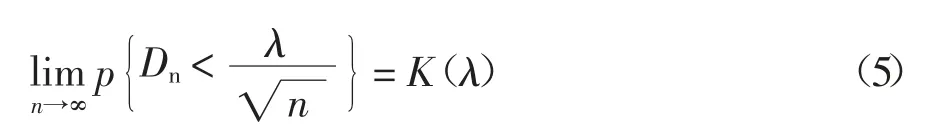
其中，

根据此定理得到Kolmogorov-Smirnov 分布的分位数：

于是对于样本（x1，x2，…，xn），可算出 Dn的观测值：

若Dn≥Dn，1-α，则拒绝H0，即认为F（x）≠F0（x）；

若Dn＜Dn，1-α，则接受H0，即认为F（x）=F0（x）.

3 结果与讨论

3.1 表面风压特性

限于篇幅，本文选取0°及270°最不利风向角下屋盖风压分布规律进行详细分析，如图8 所示.

无论是刘强东“第四次零售革命”的概念，抑或是马云的“线上、线下、物流相融”的理论，其于未来零售业的探索从最初起便开始从线上向线下布局。

0°风向角下的迎风区域为B 指廊左边缘和A 指廊端部.悬挑屋檐局部由于风上吸下顶产生较大掀力.B 指廊迎风屋檐转角处平均风压系数最大为-1.0.靠近壁面处气流经过右侧天井区域会产生回流，天井起到引流作用，其左右两侧屋盖平均风压系数在-0.4 左右.在最右侧屋檐处平均风压系数较小，为-0.2.B 指廊两处天井附近区域由于受到高屋檐和开洞影响，流场复杂，平均风压系数在-0.7 左右.A指廊端部区域由于迎风角度倾斜会形成三角翼涡，平均风压系数为-0.5.D 区域为中间高四周低的拱形形状，在0°角下，气流经过类“人字形屋顶”，在前坡区域气流发生撞击产生正压而后向上分离，分离点移动到下游屋脊处，使背风坡吞没于分离区中受到吸力.

0°风向角下周边建筑的干扰对航站楼屋盖平均风压系数等值线分布规律影响总体不大，最大负压值略有减小.试验段航站楼周边建筑干扰主要为左侧35 米高的建筑.气流经过此建筑时会发生分流，由于建筑横向尺寸小，形成无流动再附的尾流区.试验结果反映尾流对A 指廊端部影响较大，其余部分影响较小.基本处于负压状态，屋檐及转角等区域附近的平均风压系数绝对值和变化梯度最大，其余部位变化较平缓.

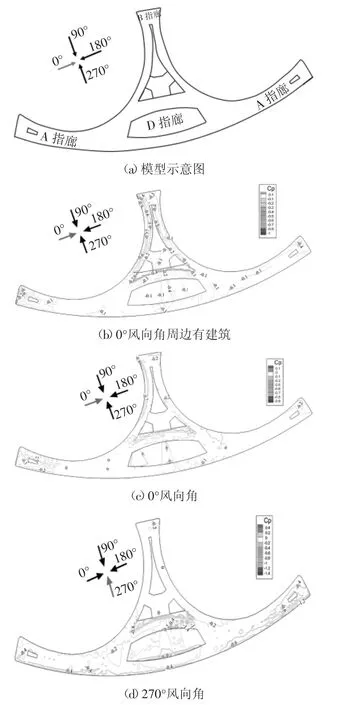
图8 屋盖典型风向角下平均风压系数等值线Fig.8 Contours of the mean wind pressure coefficients on the roof under typical wind directions

3.2 平均风压系数空间分布规律

限于篇幅，本文仅给出了0°及最不利风向角270°风向角下各测点的平均、脉动风压系数，分别如图9、10 所示.

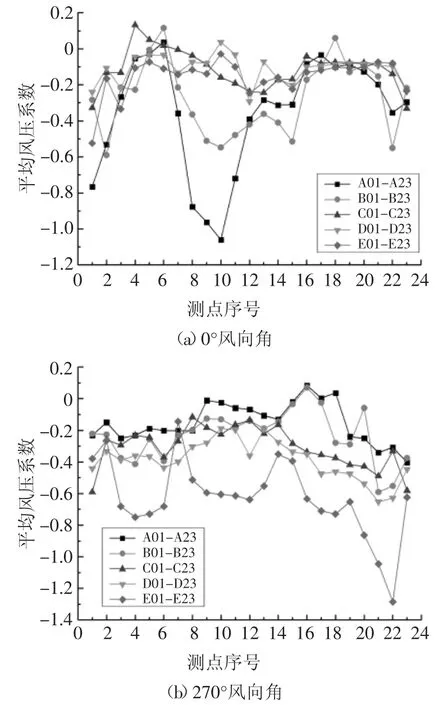
图9 典型测点平均风压系数空间分布图Fig.9 Spatial distribution of the mean wind pressure coefficients of typical taps

在270°最不利风向角下，航站楼右边缘为迎风区域，迎风宽度较大，最大负压出现在C 指廊屋檐角部区域，平均风压系数达到-1.4.在中间第三层屋盖D 缓坡区域，由于气流分离附着作用，表现出吸力较小，平均风压系数接近0.气流在经过D 屋檐时再次发生分离，分离线附近平均风压系数在-1.0 左右，由于高差影响，此处区域的流动分离较强，风压梯度较大.B 指廊区域受高顺风深度，分离附着影响，负压值较小，平均风压系数接近于0.

由图9、10 可知，0°风向角下，A、B 线上测点的平均和脉动风压系数变化比较大.在曲线前檐中间的A7 区域发生局部风压突变的情况，主要是由于气流在A 指廊端部区域发生流动分离，A6 区域受气流再附的影响呈现正压，而A7 区域不受遮挡影响，气流在此发生分离.沿屋檐边缘走向（1-23）上分析，A、B 线上平均风压系数呈现明显先上升后下降再上升的趋势，气流在B 指廊左侧区域分离最显著.C、D、E线呈现两端波动中间平缓的趋势，平缓段平均风压系数在-0.1 左右，脉动风压系数在0.08 左右.说明气流除在AC 指廊左右两端分离明显外，其余区域基本平缓.沿屋檐从外到内方向（A-E），C、D、E 线的脉动风压系数线除左侧小部分区域外基本重合，平均风压系数变化也较小，说明这些区域基本不受气流分离附着影响.

图10 典型测点脉动风压系数空间分布图Fig.10 Spatial distribution of the fluctuating wind pressure coefficients of typical taps

最不利风向角270°下，沿屋檐边缘走向（测点1-23）分析，E 线平均风压系数变化幅度较大，A-D线其平均风压系数分布曲线呈现中间凸起两端下降趋势，屋檐轮廓线走势类似.A、B、C 脉动风压系数线基本重合且数值较小（值为0.08 左右），D 线在起点与终点区域脉动风压系数较大，E 线脉动风压系数变化幅度较大.沿屋檐从外到内方向（E-A），各线存在差异，平均风压系数绝对值呈现逐渐减小趋势，说明整个屋盖区域都受到气流分离附着的影响.

3.3 风压非高斯性判别结果及对比

结合上节的判别方法，对大型多指廊屋盖高斯区和非高斯区进行判别如图11 所示.

由上图可知，采用高阶统计量方法时，0°风向角下非高斯区域主要集中在左侧迎风屋檐、A、C 指廊角部和D 屋盖两侧区域.90°风向角下非高斯区域主要集中在A、C 指廊上屋檐、D 屋盖上屋檐和各指廊端部区域.180°风向角下非高斯区域主要集中在B指廊右侧、C 指廊上侧和D 屋盖左右端.270°风向角下非高斯区域主要集中在下侧长屋檐区域和D 屋盖左右端.采用K-S 检验方法时，0°风向角下非高斯区域集中在左侧迎风屋檐、A、C 指廊角部区域.90°风向角下非高斯区域主要集中在A、C 指廊上屋檐和各指廊端部区域.180°风向角下非高斯区域主要集中在B 指廊右侧屋檐和左侧下半部以及C 指廊端部.270°风向角下非高斯区域主要集中在下侧长屋檐区域和D 屋盖下侧屋檐.通过比较发现上述高阶统计量方法划分结果比较分散，同一区域存在不连续情况，且部分区域划分结果对风向角不敏感.出现上述结果的原因在于偏度峰度的划分依据主观性太强，且采用统一划分范围对部分测点不适用情况.KS 检验法的划分结果主要集中在迎风屋檐和拐角区域，这些区域也正是气流分离显著的区域.与高阶统计量结果相比，非高斯区域连续且覆盖范围与风洞试验分析得到的风压分布规律比较吻合.分析结果表明通过设定显著性水平的拟合检验法判断风压时程的非高斯分布，能更全面反映风压分布情况.

4 结 论

本文基于我国大型机场航站楼的刚性测压模型风洞试验，对大型多指廊屋盖的表面风压分布规律、周边建筑对该航站楼屋面风压分布的干扰效应以及非高斯风压特性进行了研究.主要得出以下结论：

1）由于周边建筑物体型尺寸较小，对航站楼屋盖平均风压系数等值线分布规律影响总体不大，最大负压值略有减小，大型多指廊屋盖结构表面风压以负压为主，在屋檐及转角区域的平均风压系数绝对值和变化梯度最大.最不利风向角为270°，由于迎风宽度较大，C 指廊迎风向屋檐转角处平均风压系数达到-1.40.整体上平均风压系数曲线和脉动风压系数曲线变化规律相似.负风压系数值沿屋檐外轮廓曲线呈现两端大中间小的趋势.

2）根据满足偏度和峰度整体变化趋势不偏离和在自身变化范围内概率保证度接近的原则和大偏度大峰度偏离现象，本文使用高阶统计量法最终确定的大型多指廊屋盖非高斯特性的判别标准为：|S|≥0.11 且 K≥4.3 或且 K≥5.

3）相比高阶统计量法，柯尔莫哥罗夫-斯米尔诺夫检验法方法更加客观，理论基础更加完善，判别结果更有规律可循.非高斯区域主要集中在气流分离的迎风屋檐、指廊拐角和受尾流旋涡影响的区域.