基于边界层风洞的下击暴流稳态风场特性数值模拟

刘志文 ，陈以荣 ，辛亚兵 ，陈政清 ，2

（1.湖南大学风工程与桥梁工程湖南省重点实验室，湖南长沙410082；2.湖南大学土木工程学院，湖南长沙410082）

下击暴流是指雷暴云中局部性的强下沉气流冲击地面后，沿径向产生的直线型水平风速，最大风速可达240 km/h（约为66.7 m/s）.根据下击暴流影响的范围分为微下击暴流（半径小于4 km）和宏下击暴流（半径大于4 km），下击暴流具有突发性，且风速变化剧烈.下击暴流会对输电线塔、建筑结构等产生破坏.已有统计表明83%的输电线塔系统破坏事故是由于下击暴流引起的.近年来研究表明，美国和欧洲大部分地区结构风荷载控制值是由雷暴风确定[1-2].Letchford 和Lombardo 建议在结构设计规范中考虑下击暴流作用[3].

下击暴流风特性研究主要包括现场实测、试验模拟和数值模拟研究等.Fujita 与Mccarthy 等[4-5]学者在20 世纪80 年代通过现场实测发现并定义了下击暴流，即强下沉气流引起的近地面强风，并总结了一系列下击暴流流场特点.由于下击暴流发生时间和发生地点随机性较强，生命周期短，覆盖范围小等特点，现场实测难度较大.

Hjelmfelt[6]通过总结宏下击暴流实测数据，指出采用冲击射流装置可以实现在试验室中模拟下击暴流流场.Wood 等[7]采用了连续稳态冲击射流模型，分别进行了数值模拟与试验模拟，得到了下击暴流作用下考虑地形影响的加速因子.Letchford 等[8]从工程角度回顾了下击暴流研究，指出采用稳态冲击射流模型模拟下击暴流流场将丢失下击暴流流场环形涡与阵风峰面等动态特点.此外，Letchford 等[9]对试验装置进行了改进，实现了喷嘴的移动，研究了喷嘴固定与喷嘴移动时下击暴流的流场特性，以及在两种流场中的立方体块表面压力分布情况.Mcconville等[10]开发了一套试验装置，采用9 组风扇来产生下沉气流，通过8 组三角形襟翼实现了瞬态下击暴流的模拟.此外，西安大略大学开发的WindEEE 风洞，是首座三维风洞实验室，可实现龙卷风、下击暴流等非良态风模拟[11].Butler 和Kareem[12]利用旋转平板对稳态下击暴流进行了试验和数值模拟.Moustafa等设计了一套多道可独立运动并实现高速旋转的斜板组成的系统，可以在风洞中模拟下击暴流水平风速风场，斜板运动方式采用CFD 方法进行了优化，风洞试验结果表明模拟得到的下击暴流水平风速风场在时间和空间上与现场实测结果有较好的一致性[13].国内学者段旻等[14]进行了带有可调节平板的稳态下击暴流风洞模拟，试验结果表明，该装置模拟的下击暴流水平风速分布与经验风剖面吻合较好.

Oseguera 和 Bowles，Vicory 以及 Li 等学者基于不可压欧拉方程并类比传统边界层经验模型，提出了下击暴流流场解析模型，但这些半经验公式并不能捕捉到下击暴流流场非稳态细节特征[15-17].CFD 数值模拟由于可以获得高分辨率的流场信息、实现精准的结构荷载估算，广泛被各国学者用于下击暴流流场研究.Hjelemfelt 等人基于微观物理全云模型，采用数值模拟对下击暴流进行了模拟；Anderson 和Mason 等人则采用冷源子云模型进行了模拟[18-20].这些学者考虑了气象方面的影响，对于面向工程的下击暴流数值模拟具有参考意义，但风工程研究侧重风对结构的荷载作用，此外简化模型也有利于工程应用.Selvam 与Holmes 采用了二维冲击射流模拟计算域并考虑了地形影响，研究了当下击暴流流场通过小山时，流场风速增加情况[21].汪之松等采用大涡数值模拟方法，考虑山脉地形影响建立了二维以及三维冲击射流模型，分析了山脉高度、间距等地貌因素对下击暴流风场的影响[22].Sengupta 和Sarkar[23]采用了数值和试验方法，对下击暴流数值模拟的湍流模型、计算域和边界条件进行了深入研究.Kim 与Hangan 采用二维冲击射流模型计算域，并选用RSM（Reynolds stress model）湍流模型计算得到了下击暴流非定常流场，研究了下击暴流阵风峰面特点以及流场的雷诺数相关性问题[24].Mason 等[25]则认为SST（Shear Stressed Transport）湍流模型在冲击射流的模拟中表现良好.Chay[26]等对多组不同直径和不同下沉气流速度的下击暴流风场进行了数值模拟.结果表明，冲击射流数值模拟方法在模拟突发风场时存在一些问题，但仍然是一种有效的下击暴流风场模拟方法[26].钟永力等[27]基于CFD 方法，采用水平平板建立了二维平面壁面射流模型，并模拟了下击暴流水平风速竖向风剖面，数值模拟结果与下击暴流水平风速经验风剖面和已有的冲击射流模型试验结果吻合较好.

在研究下击暴流风场对桥梁结构作用方面，Hao与Wu[28]利用滑移网格实现了冲击射流模型下三维移动下击暴流流场模拟，并基于有限元CSD 方法对大跨度悬索桥进行了结构动力响应分析.

综上所述，现有研究表明冲击射流模型的数值模拟和试验模拟是研究下击暴流风场的重要方法.然而，冲击射流模型通常由于喷嘴直径较小，形成的风场范围较小，导致结构试验模型较小，比较适合建筑结构下击暴流风效应研究.采用WindEEE 专用风洞进行下击暴流风对结构作用效应研究则费用相对较大.考虑到下击暴流对桥梁结构的影响主要取决于其水平风，下击暴流竖向风速对桥梁结构产生的竖向风荷载效应可以忽略，而由此导致的攻角效应则可通过改变桥梁主梁断面初始攻角来考虑.在传统大气边界层风洞中进行下击暴流风场水平风速模拟对桥梁结构下击暴流风效应研究具有十分重要的意义.

本文拟在大气边界层风洞中模拟下击暴流水平风速特性，为桥梁结构下击暴流风效应试验研究奠定基础.首先采用二维、三维冲击射流模型进行下击暴流风特性数值模拟研究，以进一步了解下击暴流风场特性；在此基础上，在边界层风洞中设置倾斜平板对下击暴流水平方向风场进行数值模拟和风洞试验研究.

1 下击暴流二维冲击射流模型模拟

下击暴流冲击射流模型是应用较为广泛的一种模型.二维冲击射流模型数值模拟相比三维冲击射流模型数值模拟，网格数量可控，可计算得到更为详细的流场发展细节.本节采用二维冲击射流模型进行下击暴流风场特性数值模拟.

1.1 计算模型

参考文献[24]确定二维冲击射流模型计算参数，即采用H/Djet=4（喷口直径Djet=600 m，喷口距壁面距离H=2 400 m），计算域整体尺寸为10Djet×10Djet进行数值模拟.为简化计算，选取对称一侧区域进行计算，计算域示意图如图1 所示.分别采用剪应力输送湍流模型SST k-ω 和雷诺应力湍流模型RSM 进行计算，RSM 模型计算时采用增强壁面处理[22].压力-速度耦合格式采用半隐式求解格式SIMPLEC（Semi Implicit Method for Pressure Linked Equation Consistent）算法求解.空间离散采用二阶迎风格式，此外，动量、湍动能、湍能耗散率和雷诺应力也采用二阶格式进行离散.计算域几何缩尺比为1 ∶2 000，计算时间步长为0.001 s[29].

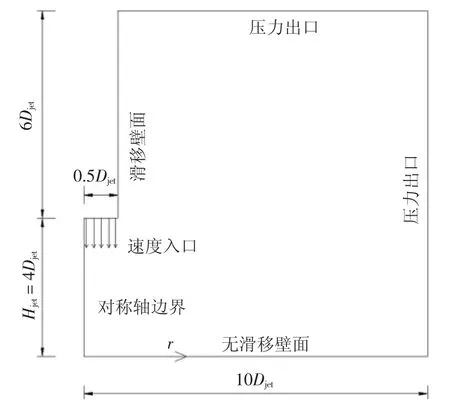
图1 计算域示意图Fig.1 Computational domain diagram

网格全部采用结构化网格，采用ICEM CFD 进行划分.考虑到冲击射流模型流体下冲于壁面处受阻后，流体流动情况复杂，因此在计算域底部处网格进行了加密处理.

y+通常用来判断边界层是否满足计算要求，y+定义为：式中：Δy 是网格中心至壁面的距离；υ 是空气的动黏度系数；τw为壁面切应力；ρ 是空气密度.

为进行网格无关性检验，采用了3 套网格进行计算，具体网格参数如表1 所示，网格示意图如图2所示.计算域边界条件设置如下：速度入口边界（Velocity inlet），来流风速 Ujet=9.6 m/s；计算域右侧、上侧为压力出口边界（Pressure outlet）；对称轴处设置为对称边界（AXIS）；入口上部壁面设置为滑移边界（Symmetry）[29].

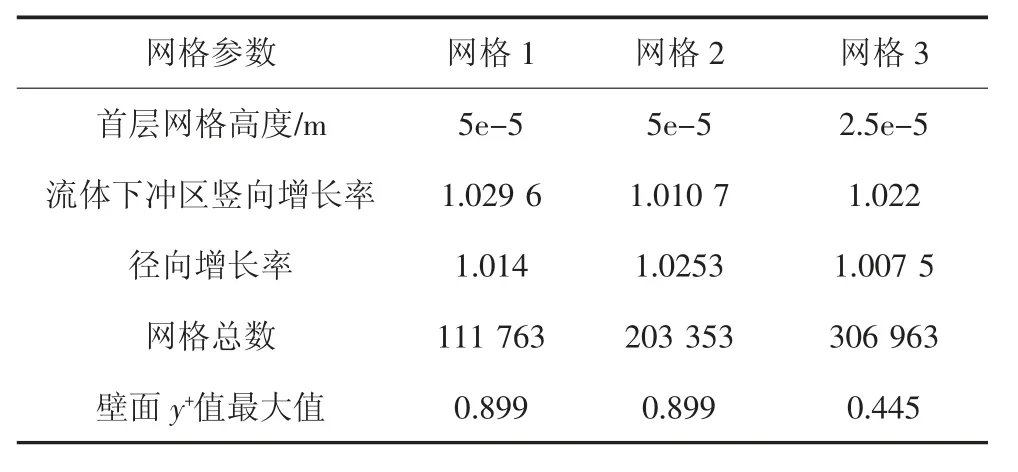
表1 2-D 冲击射流模型网格参数Tab.1 2-D mesh parameters of impinging jet model

图2 网格示意图Fig.2 Mesh schematic diagram

1.2 计算结果

1.2.1 网格无关性检验

网格无关性检验计算采用表1 中三套网格，选用SST k-ω 湍流模型进行.计算结果如图3 所示，图3（a）为径向距离r=1 Djet位置处且计算时间t=0.3 s的水平风速竖向瞬时风剖面；图3（b）为径向距离r=1Djet时，全部时程数据计算得到的水平风速竖向平均风剖面.由图3 可知，3 套网格计算结果差异较小，为节约计算资源，后续计算采用网格数量最少的网格1 进行计算.

1.2.2 计算结果

图4、图5 所示分别为二维冲击射流模型模拟得到的不同时刻流场速度云图.由图4、图5 可知两种模型计算得到的流场变化情况接近，初始时刻均产生了初始旋涡，随着时间推移开始冲击地面，产生沿水平方向的流动，同时产生了次生涡旋.

图3 网格无关性检查计算结果Fig.3 Mesh independence check calculation results

将计算周期内计算结果进行平均处理，得到两种湍流模型不同位置处水平风速竖向平均风剖面.选取距离径向位置r=1Djet以及r=1.5Djet处水平风速竖向平均风剖面，如图6 所示.由图6 可知，两种湍流模型计算结果相近，SST k-ω 湍流模型峰值速度要大于RSM 湍流模型，其沿径向移动相比RSM 湍流模型也更迅速（对比图4 图5 可知）.图7 为两种湍流模型峰值速度对应的风速时程曲线，由图7 可知风速时程曲线0～0.5 s 时两种湍流模型计算结果保持一致，0.5 s 之后SST k-ω 湍流模型结果波动较小，两者最终趋于稳定，其中速度最大时刻为t=0.3 s前后，由图4、图5 可知，t=0.3 s 前后气流冲击地面，产生了分离和重新附着，Hangan 等[24]认为：气流冲击地面过程中，产生了与主涡相反的次生涡，在两者展开并开始沿径向移动过程中对风场的径向速度起到了加速作用，本文计算结果也表明存在这种现象.

图4 流场不同时刻速度云图（雷诺应力湍流模型RSM）Fig.4 Velocity contour of flow field at different time（Reynolds Stress model turbulence model RSM）

图5 流场不同时刻速度云图（剪应力输送湍流模型SST）Fig.5 Velocity contour of flow field at different time（shear stress transportation turbulence model SST）

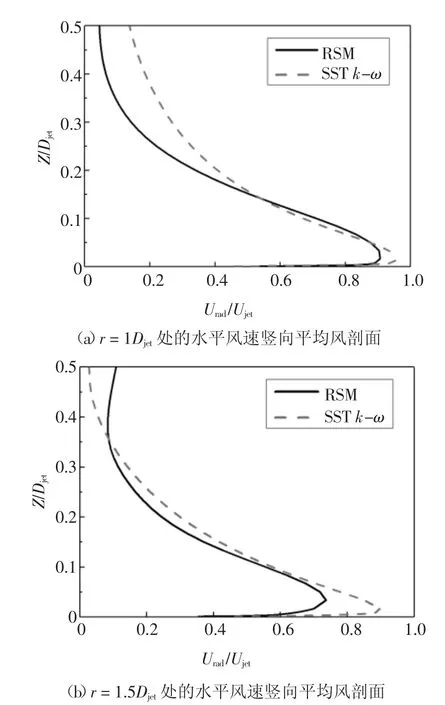
图6 不同径向位置水平速度竖向平均风剖面图Fig.6 Vertical mean wind profile of horizontal velocity at different radial position

图7 距离壁面实际高度为10 m 处风速时程曲线Fig.7 Time history curve of wind speed at 10 m from the actual height of the wall surface

图8 所示为径向位置r=1Djet时，二维数值模拟结果与NIMROD[30]和JASW[6]现场实测结果比较.为方便对比，将计算结果根据最大风速以及其对应高度进行归一处理.由图8 可知，两种湍流模型数值模拟结果与现场实测结果吻合较好，且SST k-ω 湍流模型计算结果要优于RSM 湍流模型计算结果.

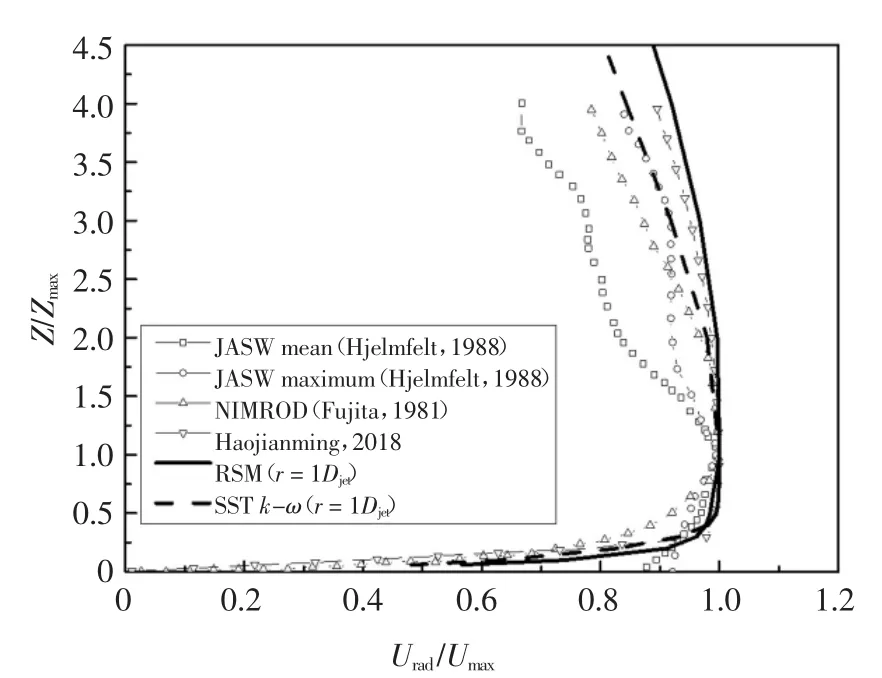
图8 r=1Djet 处平均风剖面对比图Fig.8 Comparison of mean wind profiles at r=1Djet

2 下击暴流三维冲击射流模型模拟

考虑到三维冲击射流模型可以从整体上模拟下击暴流风场特性，为了进一步比较二维冲击射流模型所模拟的下击暴流水平风速剖面特征，本节采用三维冲击射流模型进行下击暴流风场特性数值模拟.

2.1 计算模型

二维冲击射流数值模拟结果显示，计算域顶部区域流场扰动微小，为节约计算资源将计算域高度设定为8Djet，其中速度入口距离地面4Djet，保持与二维计算域一致.由于采用全尺寸计算域，原对称轴边界取消，其余边界条件与二维模拟一致.此外，三维数值模拟计算参数参照二维模拟进行设置.计算域轴对称切面图如图9 所示，计算域直径为20Djet.

图9 三维冲击射流模型计算域示意图Fig.9 3-dimensional impact jet model computational domain schematic diagram

三维数值模拟同样采用剪应力运输SST k-ω 湍流模型以及雷诺应力RSM 湍流模型进行计算.压力-速度耦合格式采用半隐式求解格式SIMPLEC 算法求解.空间离散采用二阶迎风格式，动量、湍动能、湍能耗散率和雷诺应力均采用二阶格式进行离散.计算域采用1 ∶2 000 几何缩尺，计算时间步长为0.001 s.

考虑首层网格厚度需满足无量纲距离要求，经试算后最终确定首层网格厚度为5×10-5m，网格总数为3 763 323，网格核心区域径向增长率为1.039，竖向增长率为1.15，三维网格如图10 所示，此外三维网格计算域壁面y+值均小于1.

图10 三维冲击射流模型网格示意图Fig.10 Mesh for 3-dimensoinal impact jet model schematic diagram

2.2 计算结果

图11 所示为二维、三维冲击射流模型采用不同湍流模型计算得到的径向位置分别为r = 1Djet、r =1.5Djet处对应时均水平风速竖向风剖面.图12 所示分别为径向距离r=1Djet时计算时间t=0.3 s、t=0.5 s 时二维、三维冲击射流模型采用不同湍流模型计算得到的瞬时水平风速竖向风剖面.从图11、12 中可以看出，二维、三维冲击射流模型对应的不同湍流模型数值模拟结果总体吻合较好；随着高度增长，风速先增加后减小；相对而言，采用剪应力输送SST k-ω湍流模型分别进行二维、三维冲击射流模型计算结果相对离差较小.

图11 不同径向位置平均风剖面二维、三维冲击射流模型计算结果对比Fig.11 Comparison of 2-dimensioanl and 3-dimensional impact jet models calculation results of average wind profiles with different radial positions

图12 r=1 Djet 位置不同时刻风剖面二维、三维冲击射流模型计算结果对比Fig.12 Comparison of calculation results of two-dimensional and three-dimensional impinging Jet models of wind profile at different time when r=1 Djet

3 边界层风洞下击暴流稳态风场数值模拟

3.1 计算模型

为了在边界层风洞中模拟下击暴流水平风速竖向风剖面，为桥梁结构下击暴流风效应试验研究奠定基础.参考Butler 等[12]以及段旻[14]等研究成果，考虑在边界层风洞加入一块倾斜平板以实现下击暴流水平风速竖向风剖面模拟.为此分别采用数值模拟方法和风洞试验方法进行研究.重点关注下击暴流冲击地面后形成的水平方向风速随竖向高度的变化情况，因此水平风速竖向风剖面形状以及最大风速位置是主要控制参数.

参考湖南大学2 号边界层风洞第二试验段几何尺寸确定计算域，倾斜平板中心距离速度入口4.61 m，可通过调节平板倾角α 实现下击暴流水平风速竖向风剖面模拟，分别在距离倾斜平板中心d=3.5 m、4 m、5 m、6 m 处设置风速监控点，以分析不同位置处的水平风速竖向风剖面，计算域如图13 所示.计算域边界条件设置如下：计算域左侧为速度入口边界（Velocity inlet），来流风速为 10 m/s；计算域右侧为压力出口边界（Pressure outlet）；计算域上、下侧以及下倾斜平板为无滑移壁面边界（Wall）.

图13 计算域示意图（单位：m）Fig.13 Computational domain diagram（unit：m）

采用分块结构化网格进行网格划分，为方便倾斜平板角度调整，以倾斜平板中心为圆心建立O型网格，网格各方向增长率均小于1.2，网格总数为227 484，网格示意图如图14 所示.划分网格时，以计算域形心位置为坐标原点，倾斜平板壁面y+分布如图15 所示.

图14 整体网格情况Fig.14 Mesh schematic diagram

图15 倾斜平板处y+分布情况Fig.15 y+distribution at inclined plate

3.2 计算结果

综合考虑，分别采用大涡模拟（LES）和剪应力输送SST k-ω 湍流模型进行边界层风洞下击暴流风场水平风速竖向风剖面数值模拟.时间、空间离散采用二阶迎风格式，速度-压力耦合采用SIMPLEC 算法求解，此外动量、湍动能、湍能耗散率和雷诺应力均采用二阶格式进行离散，计算时间步长为0.000 5 s.

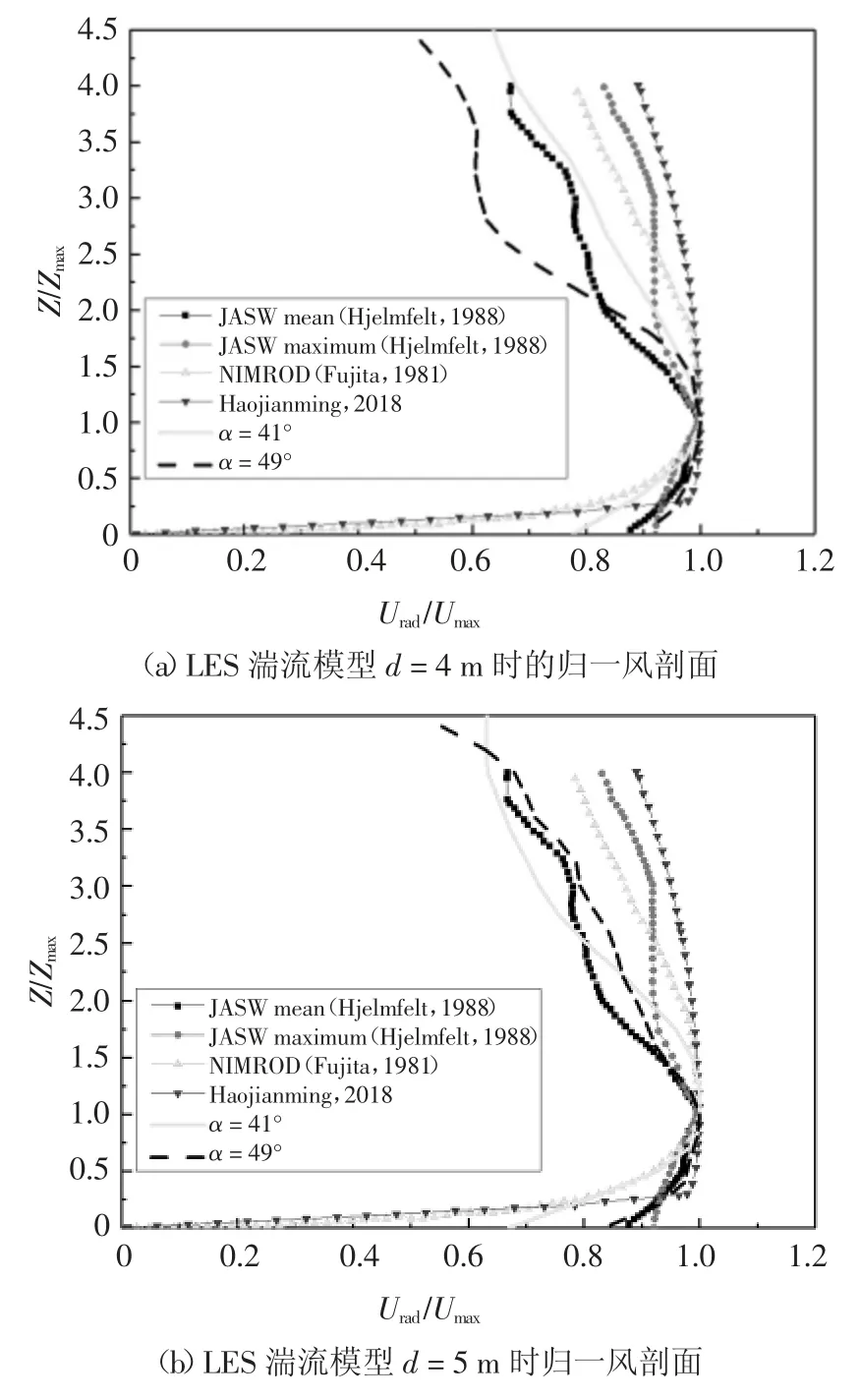
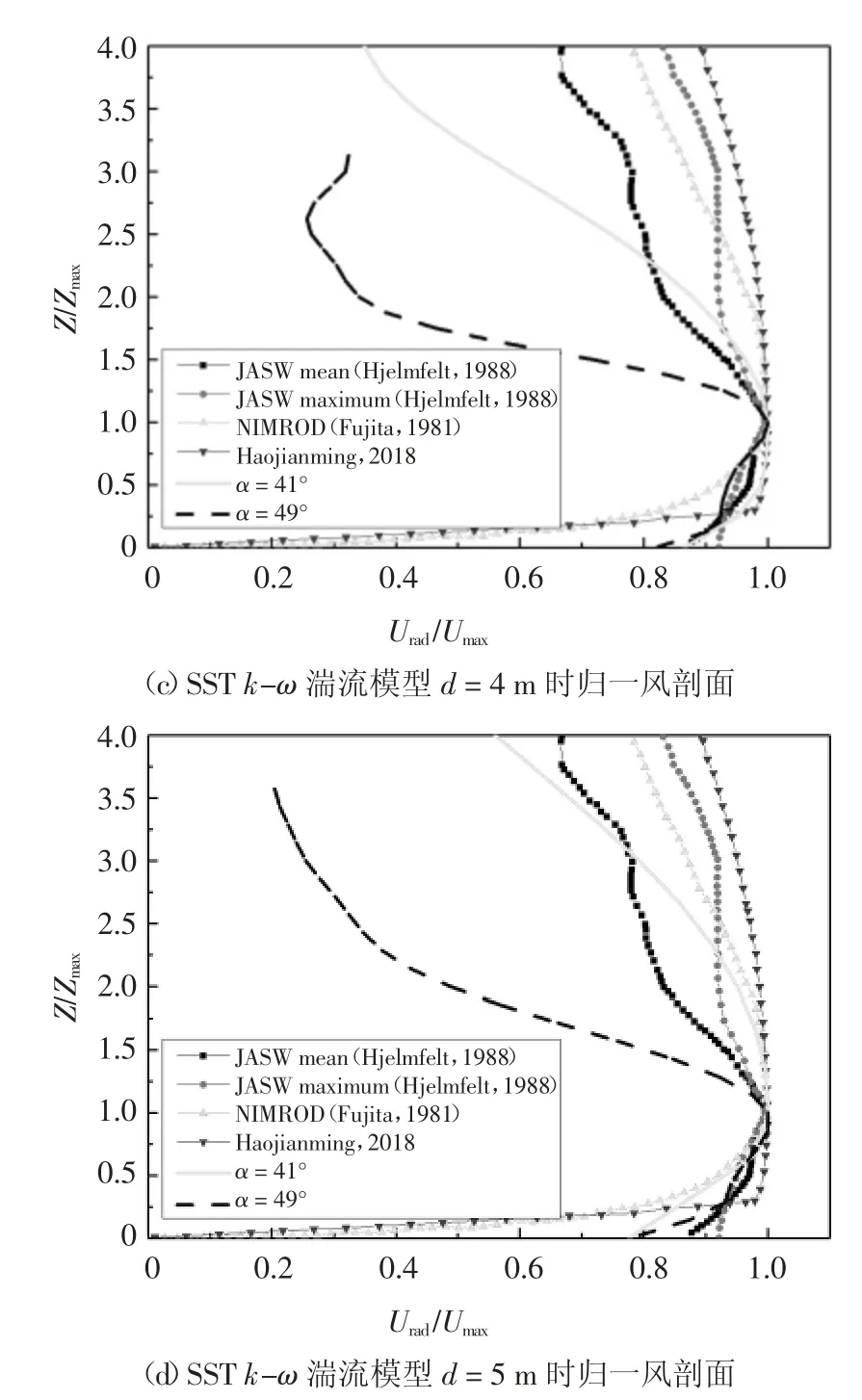
图16 数值模拟水平风速平均风剖面结果Fig.16 Numerical results of horizontal mean wind profile

为便于比较，将数值模拟结果进行时均处理，并将结果按最大风速以及其对应高度进行归一化处理.图16 所示分别为d=4 m、d=5 m 及倾角分别为α =41°、α =49°数值模拟结果.由图16 可知，倾角 α=41°～ 49°、d=4 ～ 5 m 范围时，大涡模拟计算结果与实测结果总体吻合较好.总体而言，当倾斜平板倾角合适时可实现下击暴流稳态风场水平风速竖向风剖面模拟.

Oseguera 和 Bowles，Vicory 以及 Li 等[15-17]学者根据现场实测数据建立了下击暴流水平方向竖向风剖面解析模型.图17 所示为本文数值模拟结果（SST k-ω 湍流模型，α =41°，d=4 m） 与上述解析模型比较.由图17 可知，实际下击暴流风场水平风速竖向风剖面最大风速位置距离地面为h = 70 ～80 m 左右，此外，Hjelmfelt[6]根据JAWS 实测数据总结了典型下击暴流风剖面，其中水平风速风剖面最大风速位置距离地面高度h=80 m.综合考虑，本文后续计算取h=70 m.根据实际下击暴流风场最大水平风速距离地面的位置h 和边界层风洞中模拟的最大水平风速距离风洞地面的位置h0，可以得到下击暴流水平风速风场几何缩尺比为：

风速比的确定根据常规边界层风洞模型试验方法确定.

图17 下击暴流水平风速风剖面数值模拟结果与解析模型对比Fig.17 Comparison between numerical simulation results and analytical model of horizontal wind profile of downburst

由于倾斜平板角度α 以及风速监测点距离倾斜平板中心d 不同时，形成的竖向风剖面最大风速位置距离计算域下侧的h0不一样.将部分数值模拟结果的风场缩尺比计算结果列于表2 中.由表2 可知，倾角值α 与监测点距离d 越大，最大风速位置h0增大，风场几何缩尺比λL也随之增大.

表2 数值模拟下击暴流风场几何缩尺比计算Tab.2 Calculation of geometric scale of downburst wind field in numerical simulation

4 边界层风洞下击暴流稳态风场试验模拟

4.1 试验装置

根据边界层风洞倾斜平板下击暴流水平风速竖向风剖面模拟数值模拟结果，结合下击暴流稳态流场特点，设计了边界层风洞下击暴流水平风速竖向风剖面模拟试验装置，以实现下击暴流水平风速竖向风剖面以及时变特性模拟.试验装置如图18 所示，该装置主要组成部分为：支撑架、倾斜平板、竖向对称档板、伺服电机和控制系统.倾斜平板可实现水平风速竖向风剖面模拟，由控制系统控制的伺服电机可驱动两侧竖向对称挡风板快速转动，可实现下击暴流水平风速的时变特性模拟.为了测量不同高度处风速，研制了一套专用风速测量装置.通过伺服电机控制，眼镜蛇风速仪可沿竖向方便移动，实现风速的快速测量，眼镜蛇风速仪采样频率为321.5 Hz.图19 所示为置于风洞中的下击暴流水平风速竖向风剖面模拟装置照片.

图18 下击暴流试验装置示意图Fig.18 Schematic diagram of downburst experimental device

图19 装置试验照片Fig.19 Experimental photo of test device

4.2 试验结果

试验时，通过不断调试倾斜平板的位置、倾角α以及风速测试位置距离平板中心d 的位置获得最佳风剖面.图20 给出了d=3 m、倾角α 分别为49°、60°和66°的试验结果.由图20 可知，当测试断面距离为3 m 时，倾角α 为66°时风洞试验结果比倾角α为49°和60°更接近于现场实测结果，因此固定倾斜平板角度为66°，调节风速测量装置距倾斜平板的距离，以获得最佳距离d.

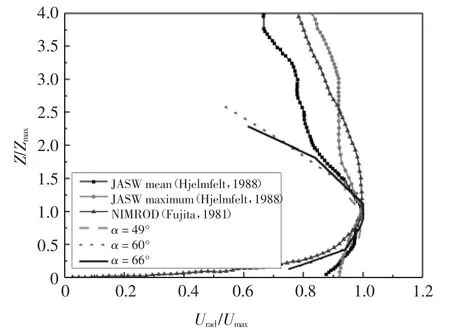
图20 倾斜平板不同倾角在d=3 m 时对应风剖面Fig.20 Wind profiles corresponding to inclined plate with different inclination angles at d=3 m

图21 分别显示了平板倾斜角度为66°时，不同监测位置水平风速竖向风剖面试验结果.从图21 可以看出，当倾斜平板的角度为66°时，d=3.5 m 和4.0 m 风洞试验结果与现场实测结果吻合较好.综合图16 和图21 可知，下击暴流水平风速剖面数值模拟结果与试验结果存在一定的差异，可能是由于风洞试验中下击暴流模拟装置支架的干扰效应引起.

图21 平板倾角为66°时不同测试断面距离对应风剖面Fig.21 Wind profiles corresponding to different test section distances when inclination angle is 66°

表3 给出了不同倾角α 及监测点距离d 处水平风速风剖面最大风速位置h0和风场几何缩尺比λL.由表3 可知，试验结果趋势与数值模拟结果总体一致，即当d 值不变时，随着倾角α 的增大，风场几何缩尺比λL增大.

此外，由于本文仅采用一块倾斜平板进行试验模拟，由图21 可知在风剖面最大风速位置以上试验结果与现场实测结果吻合效果不理想，考虑到本文试验装置模拟的最佳下击暴流风场几何缩尺比大约为λL=1 ∶200 对应的最大水平风速距离风洞底部约为h0=0.5 m，故当实际结构高度约为100 m 以内时可采用本文方法进行相关试验研究.

表3 风洞试验模拟下击暴流风场几何缩尺比计算Tab.3 Calculation of geometric scale of downburst wind field under wind tunnel test simulation

5 结 论

分别采用二维、三维冲击射流模型对下击暴流风场进行了数值模拟，对下击暴流风特性进行了研究；在此基础上分别进行了边界层风洞下击暴流水平风速数值模拟和风洞试验研究，实现了下击暴流水平风速模拟，得到如下主要结论：

1）下击暴流风场二维、三维冲击射流模型数值模拟结果与现场实测结果吻合较好，且二维冲击射流模型数值模拟结果与三维冲击射流模型数值模拟结果吻合较好.

2）边界层风洞中设置倾斜平板数值模拟结果表明：在挡板角度α、风速监测位置与倾斜平板中心距离d 合适时，形成的水平风速竖向风剖面与下击暴流水平风速竖向风剖面实测值吻合较好，为试验模拟装置设计提供了依据.

3）边界层风洞中设置倾斜平板风洞试验结果表明：下击暴流模拟试验装置在边界层风洞中可实现下击暴流水平风速竖向风剖面模拟，为桥梁结构下击暴流水平风速效应研究奠定了基础.