带电涡流缓速车桥的铰接车辆制动稳定性研究*

高志伟，李德胜，叶乐志，刘宗强

（1.北京工业大学机械工程与应用电子技术学院，北京 100124； 2.青特集团有限公司技术中心，青岛 266000）

前言

随着公路运输的发展和道路条件的改善，铰接车辆成为区段运输、甩挂运输和滚装运输的理想车型［1］，且随着铰接车辆载质量和行驶速度逐渐提高，车辆制动负荷过大严重威胁行车安全。目前，缓速器已在重型车辆和大中型客车上普遍安装［2－3］，对于铰接车辆而言，为减小主制动器的磨损并保证制动稳定性，铰接车辆安装缓速器将成为必然趋势。目前普遍在牵引车上安装缓速器，但制动时由于挂车质量大可能产生的“冲撞”和“折叠”等严重问题，制约了缓速器在铰接车辆上的广泛应用。

为解决铰接车辆的制动稳定性问题，国内外做了深入的研究。Tetsuya Kaneko等人建立了8自由度车辆非线性运动方程，详细分析了鞍座的受力，模拟了发生折叠的过程［4］。黄朝胜等人建立了铰接车辆整车数学模型，对车辆的折叠、甩尾、侧翻和转向瞬态响应等工况进行了仿真［5］。Skotnikov等人考虑了铰接车辆的簧载质量和非簧载质量，建立了整车模型，在鞍座部位设计了一种旋转制动器及其闭环控制系统，并验证了方案的可行性［6］。Islam等人建立了牵引车铰接多个挂车的动力学模型，为铰接多组挂车的情况提供了理论依据［7］。许沧栗研究了缓速器安装在牵引车上的联合制动系统方法并对原有气压制动回路进行了修改［8］。何仁等对在牵引车上安装缓速器的铰接车辆整车模型、轮胎模型、不同路况、缓速器挡位的控制策略和不同制动强度下的联合制动等方面均进行了研究［9－12］。杨佩钊对安装发动机排气制动的铰接车辆进行了稳定性分析，考虑了制动系统的延迟特性，仿真分析了不同工况下的制动稳定性［13］。何仁等对整车气压制动系统的延迟特性及其稳定性控制进行了分析，基于AMESim和TruckSim在Simulink中的联合仿真，将制动响应时间缩短了0.19 s，提高了车辆制动的稳定性［14］。综上所述，目前的研究主要集中在车辆系统建模和制动失稳方面，很少涉及在挂车上安装缓速器和制动稳定性方面的分析研究。

因此本文中提出将缓速器安装在挂车上，以解决制动力不足和“冲撞”及“折叠”问题，为此设计了一种电涡流缓速车桥。它替代原有挂车的一根支撑桥，两侧车轮带动缓速器左右转子旋转，使定子上磁场发生周期性变化，对转子产生阻碍其旋转的转矩，对车轮进行制动。

图1 涡流缓速车桥基本结构

1 涡流缓速车桥结构和工作原理

1.1 缓速车桥的结构

结合车桥结构的轮边增速与水冷式电涡流缓速器的涡流制动原理，设计了一种用于重型铰接车辆的水冷式涡流缓速车桥，如图1所示。涡流缓速车桥主要包括轮边减速器模块、制动分泵、半桥和液冷式电涡流缓速器总成。车辆的移动通过轮胎转换为制动鼓的转动，经过轮边减速器的增速将动力传输到半轴上，半轴带动缓速器转子高速旋转。该缓速车桥在没有动力系统的挂车部位可有效解决安装和缓速制动问题。

1.2 工作原理

液冷式电涡流缓速器由带水套的定子、两个励磁线圈、两个独立的转子和连接支架组成。当集中绕制的线圈通电后产生恒定的环形磁场，在缓速器的定子、两侧转子和空气隙部位形成闭合磁路，如图2所示。由于转子齿的转动和聚磁效应，在转子对应的定子内外表面产生周期性变化的磁场，定子与转子对应部位表面的一定深度内产生感应电涡流，因此产生的涡流磁场与原磁场相互作用，对旋转的转子产生制动转矩，对车辆进行制动。缓速器定子表面产生的热量传导到水套中的冷却水，通过外部散热器散发，降低了传统风冷电涡流制动转矩的热衰退，保证电涡流缓速车桥的优良制动性能［15］。

图2 液冷式电涡流缓速器工作原理图

1.3 缓速器制动模型

缓速器工作时，励磁线圈通电，在转子、定子和空气隙上形成磁场B0，转子的旋转造成定子磁场的周期变化，在定子表层产生电涡流，激励出感应磁场Bi，稳定后的气隙磁场Bδ是由励磁线圈产生的原磁场B0和涡流产生的感应磁场Bi合成，即

在液冷式电涡流缓速器的电磁场模型中，忽略位移电流，根据麦克斯韦方程，液冷式电涡流缓速器的瞬态电磁场满足以下关系：

式中：J为电流密度；E为电场强度；σ为电导率；μ为磁导率。

由式（2）～式（6）得到

由式（7）求出 Bi，代入式（2）得到 J，对 J在集肤深度Δ内积分，可得缓速器的功率P：

式中ω为转子转动角速度。

2 涡流缓速车桥的制动性能试验

为验证涡流缓速车桥的制动性能，设计制作了样机并进行台架试验。图3为电涡流缓速车桥的试验样机。

图3 电涡流缓速车桥的样机

图4为电涡流缓速车桥一侧在不同电流下的制动转矩试验值（轮边减速比为3.947）。由图可知，在0－400 r／min制动转矩呈线性增长，在 400－1 000 r／min转速范围，转矩的增长速度略为变缓，转速超过1 000 r／min以后转矩逐渐趋于饱和。电涡流缓速车桥的制动转矩与励磁线圈的电流和转子的转速有关。缓速器的磁场由励磁线圈通电产生，电流大小决定了励磁磁场的强弱，通过对电流的调节可迅速实现对缓速器制动转矩的调节。电涡流缓速车桥由于优良的制动性能和简单的控制方式，满足铰接车辆的制动需求。

通过试验验证，以电涡流缓速车桥最大制动转矩的试验数据曲线为依据，分析缓速器不同安装位置时对车辆制动稳定性的影响。

图4 缓速车桥不同电流下的制动转矩曲线

3 车辆运动学数学模型

铰接车辆由牵引车和挂车组成，挂车通过铰链连接到牵引车上。与普通单体车辆相比，铰接车辆的运动要复杂得多。考虑缓速器的安装位置不同，制动转矩作用于不同的车轮，当安装于挂车时，制动转矩作用于挂车车轮，安装于牵引车时，制动转矩作用于驱动轮。两种安装位置不影响车辆的运动分析，只影响作用车轮的运动分析。

3.1 铰接车辆的运动学方程

铰接车辆的制动稳定性取决于制动过程中牵引车和半挂车的侧向运动和横摆运动。本文中基于动力学原理［1，16］，对安装缓速装置的铰接车辆的纵向、横向和横摆运动进行分析。图5为铰接车辆受力图。分析前做如下简化：①将牵引车和半挂车各视为一个刚体；②忽略车辆的侧倾、俯仰等对制动稳定性影响较小的运动；③将左、右车轮等效为单轮；④将6轴铰接车辆等效为4轴，与图中地面反力Fz1～Fz4相对应。按图5由左到右的顺序，缓速器安装在挂车上时依次为转向桥、驱动桥、缓速车桥和挂车桥；缓速器安装在牵引车上时依次为转向桥、缓速车桥、挂车前桥和挂车后桥，建立了铰接车辆动力学模型。

牵引车运动方程、挂车运动方程、鞍座约束方程和载荷转称方程分别如图11～图14所示。

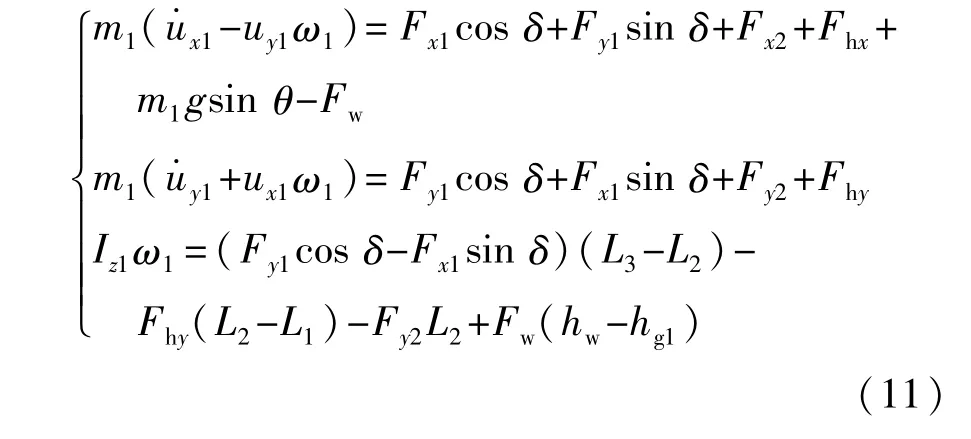
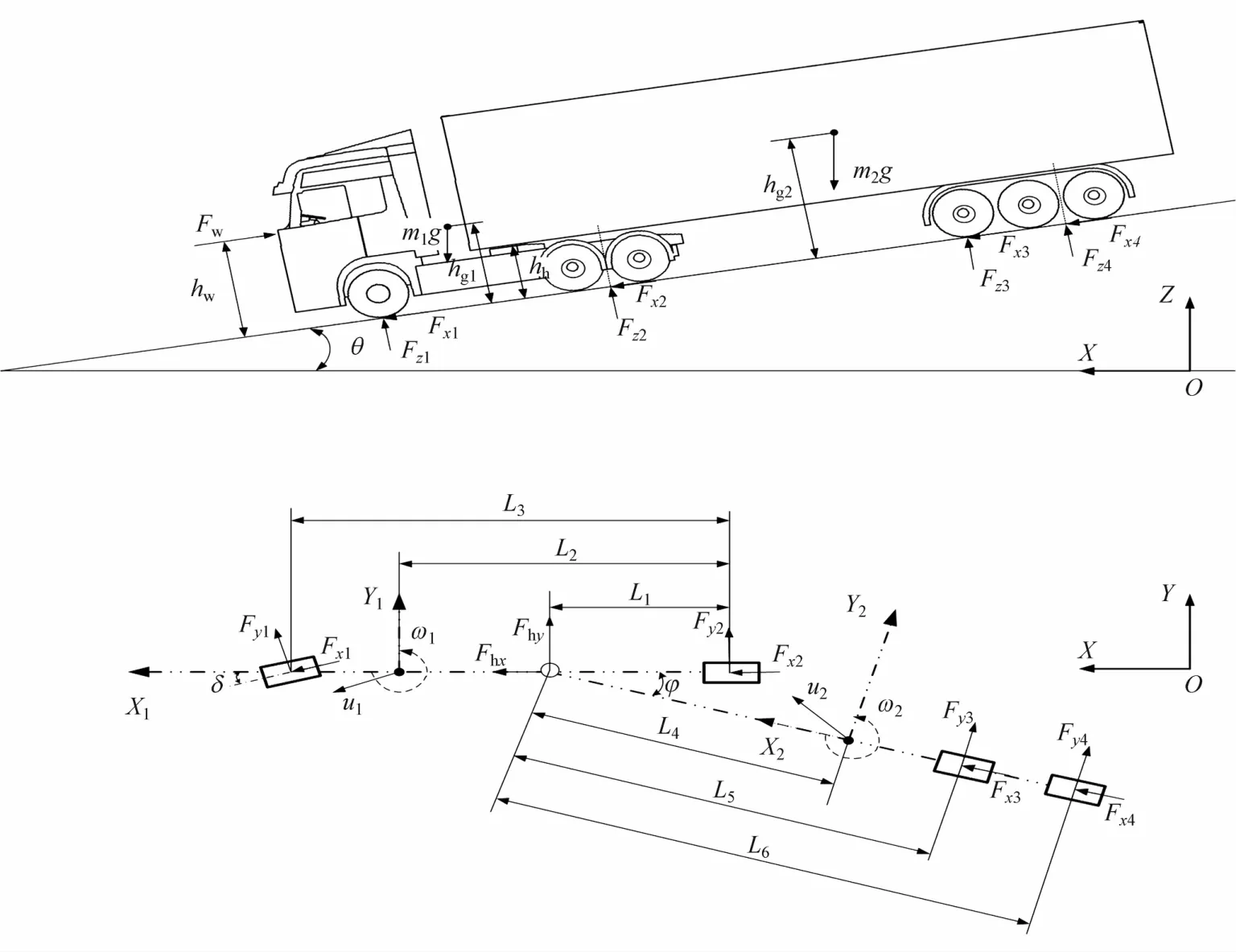
图5 铰接车辆受力图

式中：m1为拖车质量；m2为挂车质量；u1为牵引车速度；u2为挂车速度；ux和uy分别为牵引车和挂车的速度沿坐标系的分量；ω1和ω2分别为牵引车和挂车的横摆角速度；Fw为汽车空气阻力；Fxi、Fyi和Fzi分别为车轮所受的纵向力、侧向力和垂直载荷（i＝1，2，3，4，按由左到右的顺序表示 4根车桥或其上车轮的属性）；Fhx、Fhy和 Fhz为铰链处鞍座孔3个方向的受力；Iz1为牵引车的转动惯量；Iz2为挂车的转动惯量；φ为铰接角；δ为前轮转向角；θ为道路的坡度角；L1为铰接点到驱动桥的纵向距离；L2为牵引车质心到驱动桥的纵向距离；L3为牵引车转向桥到驱动桥的纵向距离；L4为铰接点到挂车质心的纵向距离；L5为铰接点到涡流缓速车桥的纵向距离；L6为铰接点到挂车桥的纵向距离；hg1和hg2分别为牵引车和挂车的质心到地面的垂直距离；hw为迎风阻力到地面的垂直距离；hh为铰接点到地面的垂直距离。

3.2 车轮运动方程

车轮在制动时，摩擦制动器对车轮提供制动力矩Tb，阻碍车轮的转动。当缓速器工作时，又给车轮施加一个制动转矩Tr。图6为无缓速器作用的车轮的受力分析图、安装于挂车的缓速车桥对应车轮的受力分析图和缓速器安装于牵引车时作用车轮的受力图。图中：Jw为车轮的转动惯量；ωw为车轮的转动角速度；G为轴的垂直载荷；uw为车轮中心的线速度；Fo为车轴对车轮产生的推力；Fi为车轮的惯性力；r为车轮半径。当仅使用缓速器来制动，摩擦制动器不工作时，Tb＝0。

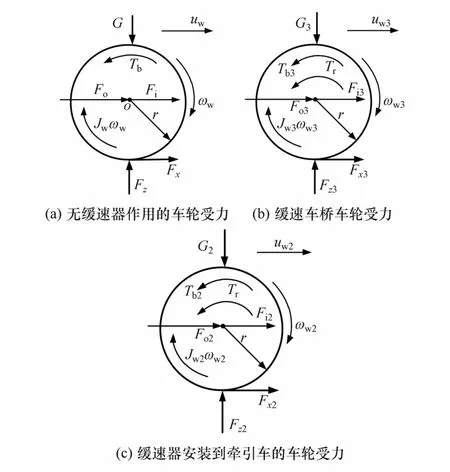
图6 车轮受力图

缓速器安装于挂车时车轮运动方程为

轮胎模型采用TruckSim软件内部的模型，联立车辆运动方程式（11）～式（14）、轮胎模型和缓速器安装于挂车或牵引车两种情况下的车轮运动方程式（15）或式（16）可分别求解出缓速器安装于挂车和牵引车两种情况下的车辆各参数。

3.3 常规路况

在进行车辆制动稳定性分析时，路面状况起到重要作用，不同附着系数的路面所能提供给轮胎的摩擦力不同，因此讨论不同路面附着系数下的制动稳定性和涡流缓速车桥的使用边界条件具有重要意义。不同路面的附着系数见表1［1］。

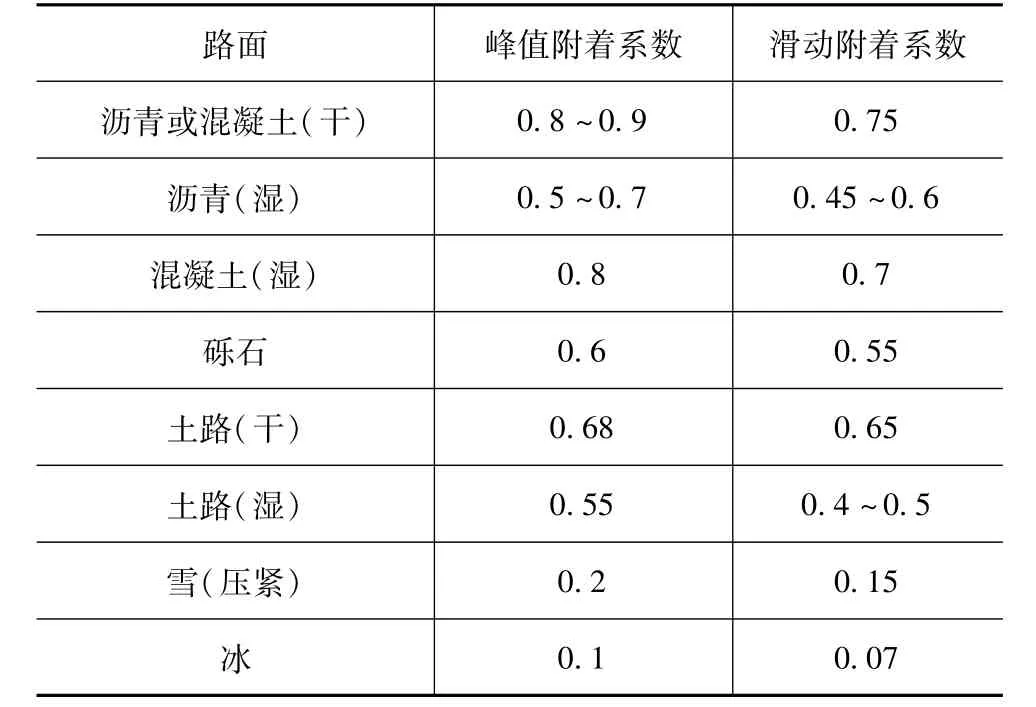
表1 路面附着系数

4 整车制动稳定性仿真

以整车数学模型为基础，电涡流缓速车桥样机的试验制动性能为依据，运用TruckSim-Simulink进行联合仿真，建立整车不同工况的稳定性仿真模型。分别在空载和满载情况下，分析缓速器安装在挂车和牵引车上车辆的运行状态，并进一步分析缓速器在不同附着系数的路面制动时的稳定性。在TruckSim中建立空载和满载的整车模型的基本参数见表2。

表2 空载和满载时整车的基本参数

4.1 仿真工况

缓速器经常在长下坡路况和持续制动时使用，由于我国山路的特点，在长下坡路况往往伴随着弯道，这也是重型铰接车辆事故多发的主要原因。基于上述路况信息和GB7258—2017［17］中对辅助制动装置的相关规定，道路取7%的坡度，将车辆行驶的弯道路面设置为一个周期的正弦曲线，如图7所示。车辆仿真的初速度为60 km／h，考虑不同路面附着系数时的车辆运行状态。

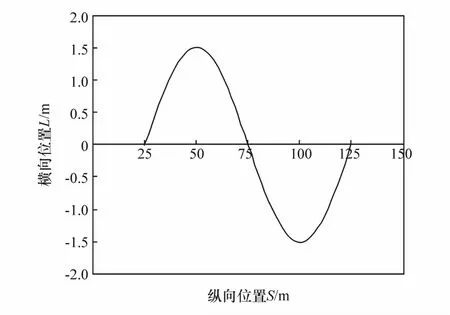
图7 弯道曲线

4.2 缓速器不同安装位置的制动稳定性分析

缓速器作为辅助制动装置，能有效保护摩擦制动器，在实际使用中往往具有独立的控制系统且单独使用，在长下坡路况优势明显。当缓速器单独工作时，考虑安装于牵引车传动系和挂车部位的两种安装位置时的车辆稳定性具有重要意义。下面对路面附着系数为0.8，摩擦制动器不工作，缓速器单独提供制动力矩，车辆行驶1.25 s后开始进行缓速制动的工况，空载和满载状态下，缓速器安装于牵引车和挂车上的两种情况的运行状态进行仿真分析。仿真结果分述如下。

4.2.1 不同安装位置对铰接角的影响

铰接角是直接反映铰接车辆是否发生“折叠”现象的重要参数。缓速器的安装位置不同对车辆制动时的稳定性影响不同。

图8为空载和满载两种情况下缓速器不同安装位置时车辆铰接角的变化规律。由图8（a）可知，车辆空载时，缓速器安装到挂车部位的铰接角曲线比牵引车缓速器变化的幅值更小。由于挂车空载时的惯性小，两种安装位置情况下车辆铰接角的变化均不明显，曲线幅值较低。如图8（b）所示，当车辆满载时，缓速器安装于牵引车部位，铰接角已经不按规律变化且曲线幅值过大，车辆无法恢复到稳定运行的状态。而缓速器安装于挂车部位在满载状态下仍能维持车辆制动时的稳定运行。

图8 缓速器不同安装位置铰接角的变化

4.2.2 缓速器不同安装位置对鞍座受力的影响

鞍座是连接牵引车和挂车的重要部件，两个车体的运动和受力在此处耦合，鞍座的纵向力和侧向力与车辆的稳定性和行车安全密切相关，为评价是否发生“冲撞”的重要参数。

图9为车辆空载状态下，缓速器不同安装位置时鞍座所受的纵向力和侧向力。由图9（a）可知，当在牵引车上安装缓速器时鞍座处所受纵向力为正，说明挂车在“冲撞”牵引车，缓速器安装于牵引车所受的纵向力的绝对值是安装于挂车的2倍左右。由图9（b）可知，鞍座所受侧向力变化规律稳定，说明空载时挂车部位的惯性不大，缓速器安装在不同位置时车辆皆可保持良好的运行状态。

图10为车辆满载制动时，缓速器安装于不同位置时鞍座所受纵向力和侧向力。由图可知，缓速器安装到挂车上时鞍座所受纵向力为负，满载的挂车拽着牵引车且鞍座的纵向力和侧向力的受力曲线规律波动。而缓速器安装于牵引车的鞍座所受纵向力为正，牵引车受到惯性更大的挂车的冲撞，且鞍座所受纵向力和侧向力的幅值绝对值过大，变化已无明显规律，说明车辆已经发生丧失稳定性的危险现象。

对比车辆空载和满载两种情况，车辆的质量越大，鞍座处所受力的绝对值越大（见图9（a）和图10（a）），缓速器安装于挂车部位，在空载和满载时均能保持车辆制动的稳定性。而安装于牵引车部位，在空载时可保持制动稳定，当车辆满载时，会发生严重的失稳现象。

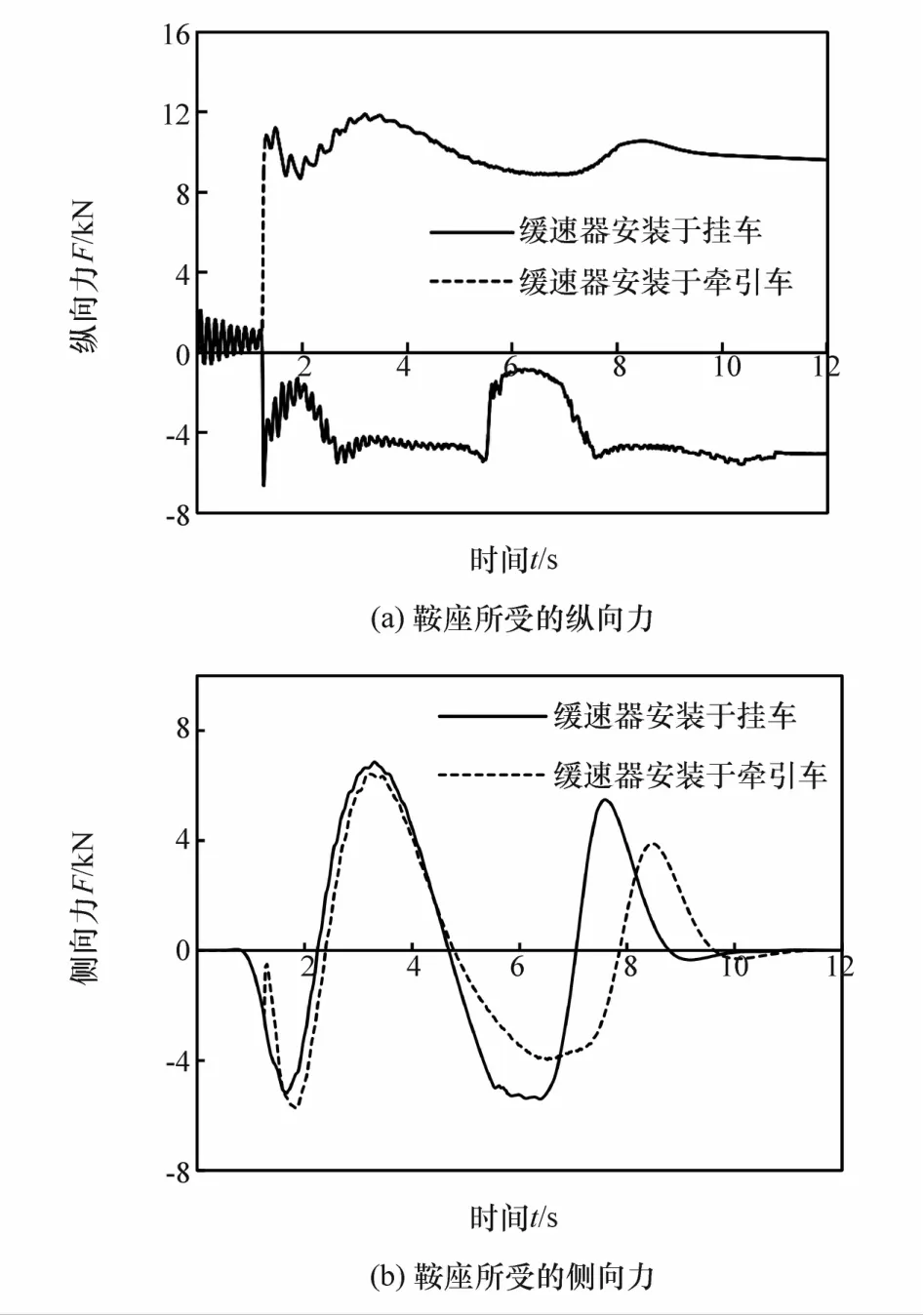
图9 空载时鞍座处受力

4.3 不同路面附着系数时缓速制动稳定性分析

上面对附着系数为0.8的路面仿真结果表明，安装于挂车上的涡流缓速车桥更有优势。当车辆在低附着路面行驶时，轮胎容易发生滑移。由表1可知，轮胎发生滑移时附着系数更小，因此探讨不同路面附着系数下两种安装位置对车辆稳定性的影响及其使用的边界条件具有重要意义。根据前面的分析，在高附着路面，车辆满载时缓速器安装于牵引车已经发生了“冲撞”和“折叠”现象，车辆无法稳定运行，下面进一步分析车辆空载时，不同路面附着系数时缓速器安装于牵引车和挂车两种情况下的铰接角幅值的变化规律，结果如图11所示。由图11可见，在相同附着系数的情况下缓速器安装于挂车要比安装于牵引车的铰接角变化幅值小，安装于牵引车的缓速器在附着系数大约为0.3时，铰接角幅值的变化率开始迅速增大，车辆逐渐失去制动时的稳定状态。而缓速器安装于挂车部位时，附着系数大约为0.2时，车辆的铰接角幅值变化率迅速增大。在低附着系数时，缓速器装于牵引车部位，车辆存在发生折叠的风险，严重威胁行车安全。

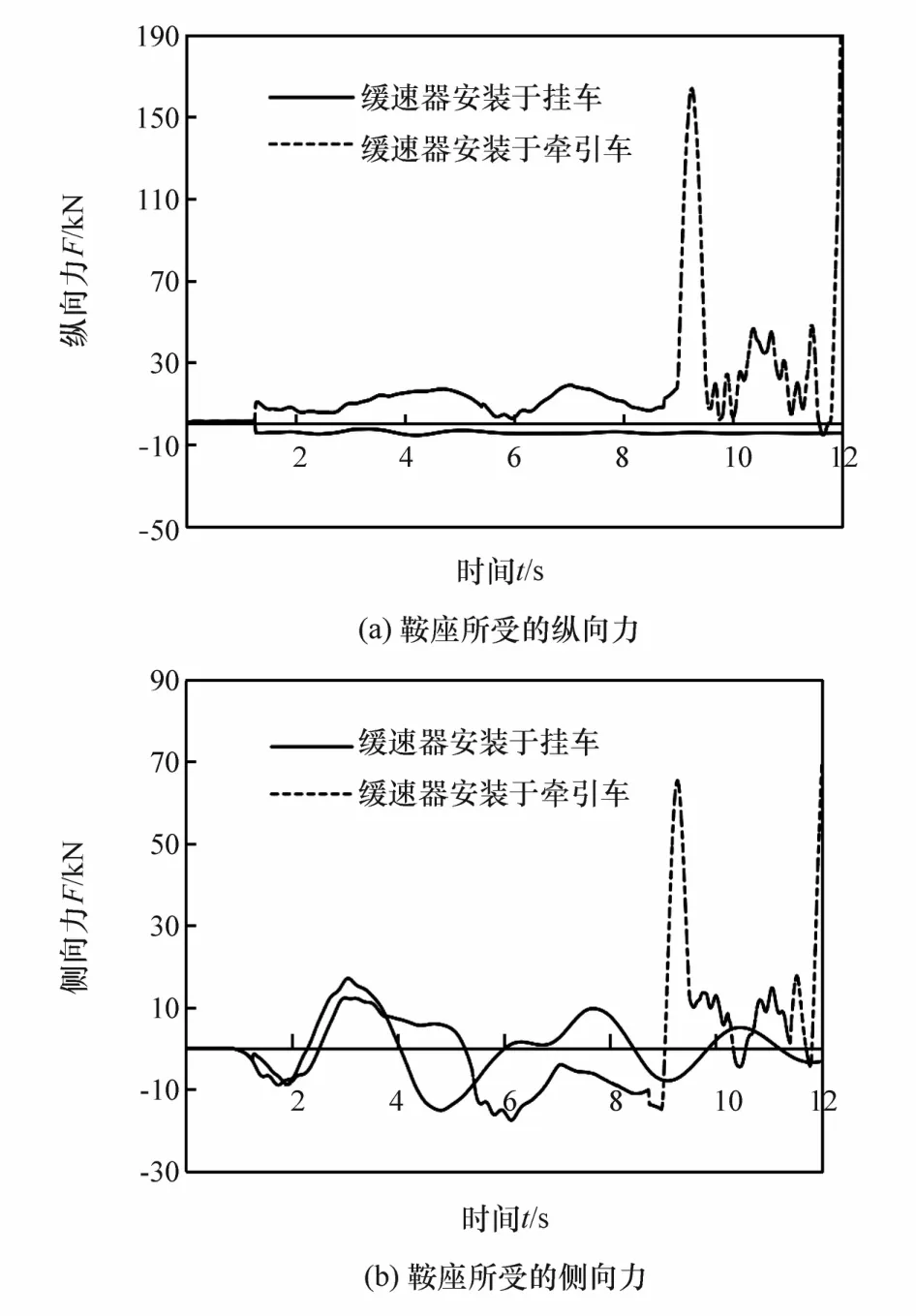
图10 满载时鞍座处受力

图11 不同路面附着系数下铰接角幅值变化规律

通过以上分析，在长下坡路况，比较车辆空载和满载时缓速器安装于牵引车和挂车的情况，安装于挂车的涡流缓速车桥可以更好地维持车辆制动时的稳定性。当牵引车缓速器工作时，为维持稳定性，需要挂车部位的摩擦制动器也提供相应的制动力，但是会加剧挂车部位的摩擦制动器的磨损，影响制动器的寿命。而安装于挂车部位的缓速车桥可直接对挂车制动，无须摩擦制动器提供制动力，可保护摩擦制动器的有效性，保证制动器的使用寿命，减小维修成本。

5 结论

建立铰接车辆的动力学模型，并进行了联合仿真分析。基于研制的一种水冷电涡流缓速车桥进行台架试验的数据，重点研究了车辆空载和满载时缓速器分别安装于牵引车和挂车时的车辆制动稳定性问题，得出如下结论。

（1）车辆空载和满载时，缓速器安装于牵引车部位比安装于挂车部位更容易使车辆发生“折叠”和“冲撞”的失稳现象，且车辆满载制动时的铰接角变化幅值和鞍座处的受力都比空载制动时大。

（2）车辆空载时，不同路面附着系数的情况下，缓速器安装于挂车部位比安装于牵引车部位铰接角的幅值要小，且路面附着系数较小时，缓速器安装于牵引车存在发生折叠的危险；满载时总质量49 t的铰接车辆，在高附着路面行车，缓速器安装于牵引车会发生折叠现象，而缓速器安装在挂车，则可以安全运行。