基于自适应代理模型的汽车乘员约束系统优化设计*

刘 鑫，刘 祥，周振华，胡 林

（1.长沙理工大学，道路灾变防治及交通安全教育部工程研究中心，长沙 410114；2.长沙理工大学，工程车辆安全性设计与可靠性技术湖南省重点实验室，长沙 410114）

前言

当汽车发生碰撞时，汽车乘员约束系统是保障乘员生命安全最有效的防护装置［1］，它包括安全气囊、安全带、安全座椅和吸能转向系统等装置。大量____的实践表明［2－3］，良好的汽车乘员约束系统可大幅减少乘员损伤并降低死亡率。因此，在汽车安全性设计中，汽车乘员约束系统的安全防护性能是研究的重点和热点。

针对汽车乘员约束系统安全性的研究，传统的方法大多数是基于实车碰撞试验来验证汽车乘员约束系统的安全性［4－5］。然而，该方法过程复杂且成本高昂，导致其工程实用性较差。虽然，CAE技术的应用能在一定程度上弥补传统试验方法的缺陷，但通过CAE技术对汽车乘员约束系统进行优化时，耗时的数值模型与高昂的计算成本往往会导致优化求解失效、约束违反等问题，从而造成极低的优化效率。因此，为提高优化效率，基于代理模型［6－9］的优化设计方法在工程优化问题中得到了广泛应用。该方法主要是通过简单的显式函数来构建真实模型的激励与响应的映射关系，并结合优化方法实现近似优化问题的求解。然而，由于汽车乘员约束系统的代理模型具有高维和强非线性的特点，须大量样本信息来构建整个模型，效率低下且易造成矩阵奇异。因此，保证汽车乘员约束系统代理模型的精度，并有效减少此类高维问题的样本数量来提高计算效率，是目前汽车乘员约束系统优化设计问题的关键。

本文中提出了一种基于自适应代理模型的汽车乘员约束系统优化设计方法。该方法首先通过仿真软件建立了汽车乘员约束系统数值模型，并通过实车碰撞试验来验证数值模型的有效性；然后，采用拉丁超立方试验设计方法对样本点进行采样，并结合逆向形参数法来获取径向基函数的最优形参数，争取通过少量真实仿真模型的计算来获得所需精度的代理模型；最后，通过隔代映射遗传算法（IP-GA）对汽车乘员约束系统进行优化设计，从而确保汽车乘员的安全性。

1 仿真模型的建立与验证

1.1 模型的建立

针对某微型客车的尺寸结构与相关特性，在该客车发生100%正面碰撞的工况下，运用仿真软件建立了驾驶室内乘员约束系统的数值模型，如图1所示。该数值模型主要包括微型客车车体模型、HybridⅢ50百分位假人模型和三点式安全带模型。基于该系统数值模型可获得乘员身体各部位在汽车发生碰撞时的动态响应与损伤评价指标。

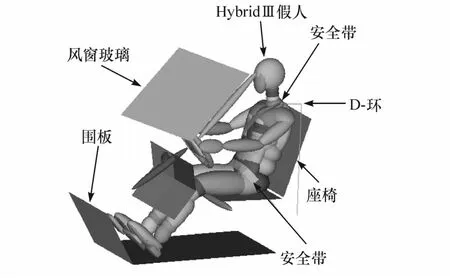
图1 乘员约束系统数值模型

1.2 模型验证

汽车乘员约束系统数值模型建立后，其准确性须通过实车碰撞试验来验证。本文中的试验验证按照（GB11551—2003）乘用车正面碰撞的乘员保护中规定的细则进行，将得到的实车碰撞试验结果与数值模型仿真结果进行对比，并不断修改数值模型文件，使仿真数据与实车碰撞数据基本吻合，方可确认该数值模型能真实反映汽车碰撞发生时乘员各身体部位的动态响应。

图2为假人动态响应曲线的仿真结果与试验结果的对比。由图2可见，各响应曲线的趋势和峰值出现的时刻基本一致。表1则是与图2对应的数值对比。由表1可见，假人损伤响应指标的误差基本都在10%以内。因此，该数值仿真模型基本能准确反映汽车发生碰撞时的乘员身体各部位的动态响应，可在此模型上进行优化设计。

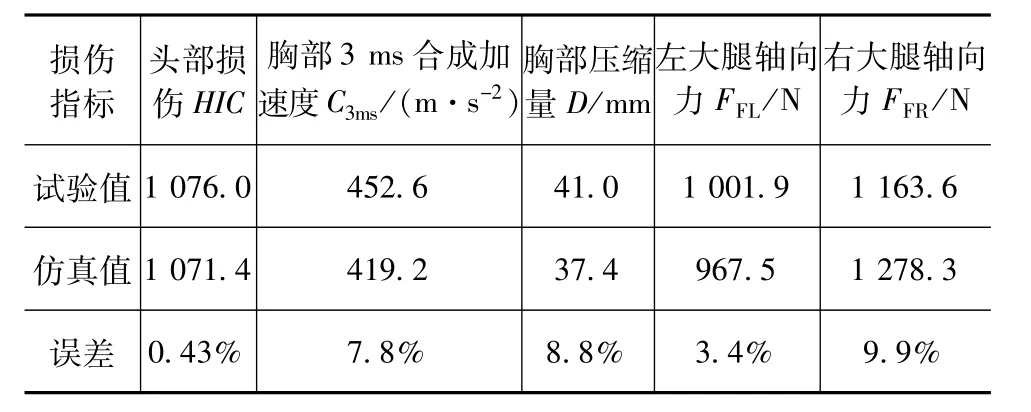
表1 假人损伤响应仿真与试验结果对比

2 汽车乘员约束系统优化问题的描述

当汽车发生碰撞时，乘员损伤涉及多个身体部位。为准确评价车内乘员的受伤情况，使用加权损伤准则WIC［10］这一综合评价指标对乘员受伤害情况进行评价，并作为该汽车乘员约束系统的优化目标，其计算公式为

式中：HIC为头部综合损伤指标；C3ms为胸部3 ms合成加速度；D为胸部压缩量；FFL为左大腿轴向压力；FFR为右大腿轴向压力。

同时，选取安全带上挂点位置X1、安全带锚点位置X2、座椅刚度系数X3和安全带的初始应变X4作为该汽车乘员约束系统的设计变量，并将头部综合损伤指标HIC、胸部3 ms合成加速度C3ms、胸部压缩量D、左大腿轴向压力FFL和右大腿轴向压力FFR作为约束条件，则优化问题可描述如下：

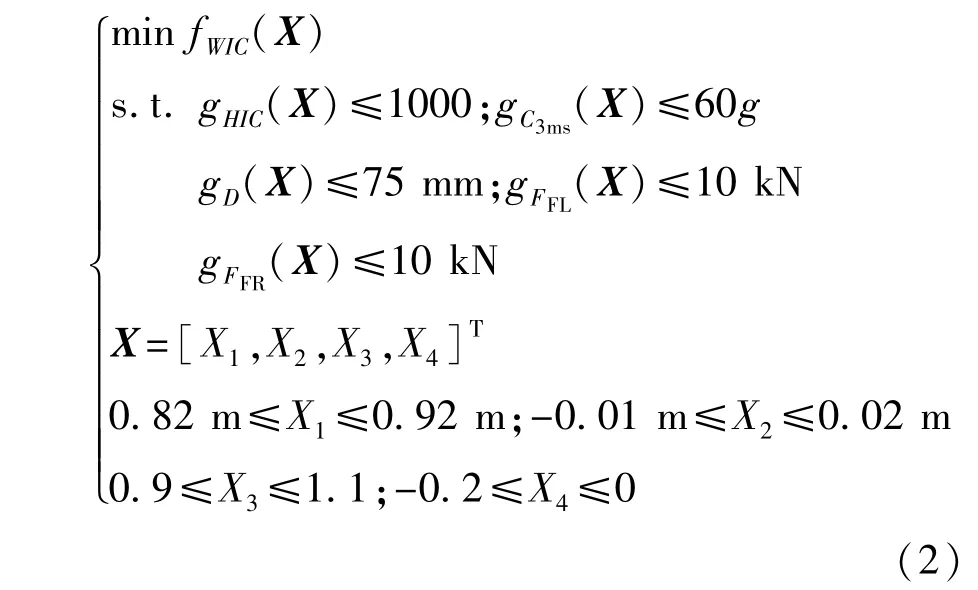
式中：fWIC为加权伤害准则WIC值；gHIC为人体头部损伤HIC；gC3ms为胸部损伤的C3ms值；gD为胸部压缩量D值；gFFL为左大腿轴向压力FFL；gFFR为右大腿轴向压力FFR；X为设计变量。

图2 假人动态响应曲线仿真与试验结果对比

3 汽车乘员约束系统特性参数优化

由于汽车乘员约束系统的数值分析模型非常复杂，采用传统的优化方法效率根本无法满足设计要求，因此，本文中首先通过拉丁超立方试验设计方法（Latin hypercube design，LHD）［11］获得试验设计样本点，然后利用径向基函数和逆向形参数法构建汽车乘员约束系统的代理模型，并采用IP-GA遗传算法对构造的近似优化问题进行求解，以获得汽车乘员约束系统的最佳匹配参数。

3.1 试验设计方法

试验设计是通过设计空间中的部分样本点来反映整个设计空间的特性。采用拉丁超立方试验设计方法来获取初始样本点。首先，采集N个样本点ΩX＝｛X1，…，XN｝，并基于后续方法来获得一组“待选形参数”；然后，将样本点 ΩX＝｛X1，…，XN｝分为“构建组”｛X1，…，｝和“测试组”{，…，XN}两组样本点，其中“构建组”样本点与每个“待选形参数”相结合来构建其对应的代理模型，而“测试组”的样本点则作为测试点验证该代理模型的精度。

3.2 径向基函数代理模型

径向基函数（radial basis function，RBF）［12］是一种通过样本点进行插值拟合的方法，它通过一组以待测点X与样本点Xi之间的欧氏距离为基础的径向函数进行线性组合，从而得出待测点X的响应，其表达式为

在构建径向基函数时，通过样本点和样本点的真实响应值可得到方程组：

式中：f为N维的样本点响应值矢量；w为N维的权系数矢量。如果h的逆矩阵存在，则权系数矩阵w可通过下式求得

将获得的权系数代入式（3），则最终得到径向基函数近似模型。

3.3 逆向形参数法

由上述代理模型的构建原理可知，样本点处的代理模型响应值与真实值相等，但在待测点处的代理模型响应值与真实值之间存在一定的误差，而误差的大小则与代理模型使用的核函数和形参数有关。因此，对于代理模型来说，选择合适的核函数与形参数至关重要。本文中选用高斯函数作为代理模型的核函数，并提出一种“逆向形参数法”来获得该核函数的最优形参数。其中，高斯函数的具体表达式为

式中ε为高斯函数的形参数，是大于零的常数。

首先，依次从样本点 ΩX＝｛X1，…，Xj，…，XN｝（j＝1，2，…，N）中选取 Xj作为“关键点”，并在关键点 Xj附近取 M个样本点 ΩXK＝｛｝（p＝1，2，…，M）且 ΩXK⊆ΩX来构建如下所示的“微型RBF模型”：

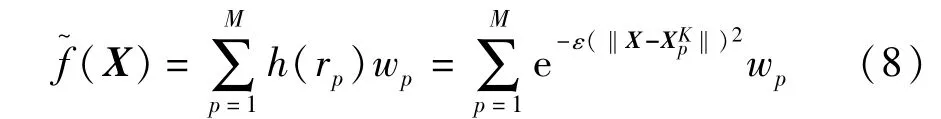
其中形参数ε与权系数w＝（w1，…，wM）T为待求的未知量。基于式（6），权系数w展开形式如下：

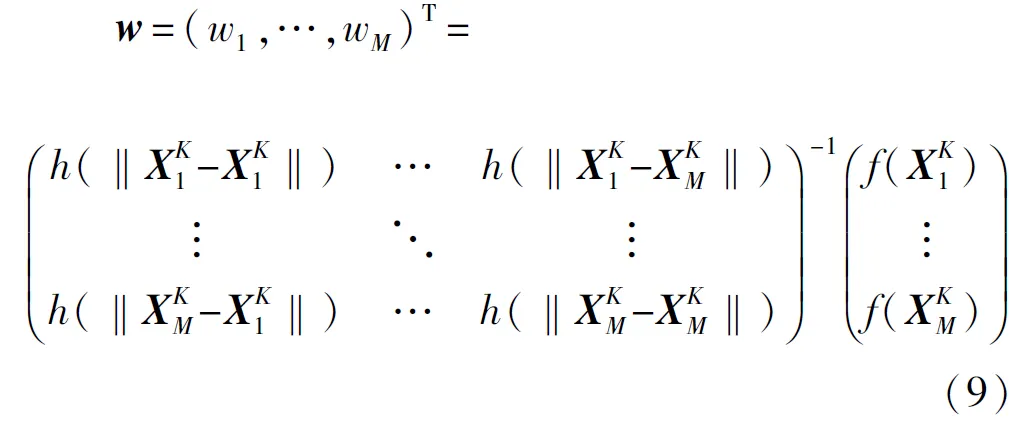
然后，将关键点Xj作为预测点代入式（8）中，并假设在 Xj处的预测值与真实值 f（Xj）相等，

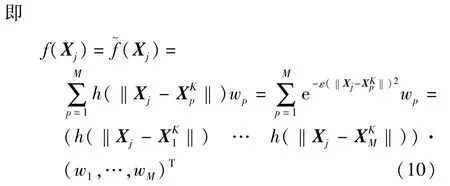
再将式（9）代入式（10）即可得到求解形参数ε的方程：

式（11）中只包含形参数ε一个未知参数，不难求解。值得注意的是，一个关键点Xj及其附近的M个样本点便可求得一个对应的形参数值，将N个样本点依次作为关键点并进行上述步骤便可获得N个形参数值，这些形参数称为“待选形参数”。将用每个待选形参数构建代理模型并对代理模型进行误差分析，选择最小误差对应的形参数作为最优形参数来构建最终的代理模型，其具体方法为：将样本点ΩX＝｛X1，…，XN｝分为“构建组”｛X1，…，｝和“测试组”{，…，XN}两组样本点，其中“构建组”样本点与每个“待选形参数”相结合来构建其对应的代理模型，而“测试组”的样本点则作为测试点来验证该代理模型的精度，并通过式（12）求出测试点的代理模型函数值与函数真实值的误差：

式中：f（Xi）为测试点的函数真实值为测试点的代理模型函数值。获得所有“待选形参数”对应的误差后，便选取最小误差对应的形参数作为最优形参数，并与样本点 ΩX＝｛X1，…，XN｝一起来构建最终的代理模型）。

3.4 近似优化问题的建立与求解

采用上述方法构建目标函数和约束函数的代理模型后，便可将式（2）所描述的汽车乘员约束系统优化问题转换成如下近似优化问题：

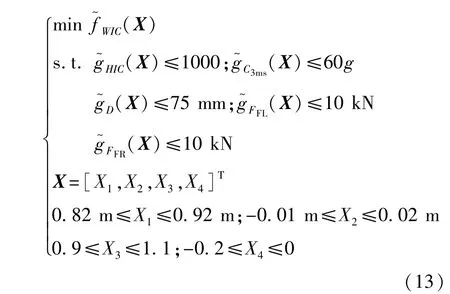
图3 乘员约束系统优化设计流程图

针对汽车乘员约束系统的优化设计流程如图3所示，具体步骤如下。

（1）利用拉丁超立方试验设计方法（LHD）在设计域空间内进行样本点采样。设置许可误差emax，置迭代步数s＝1。

（2）将所有样本点导入仿真软件，并调用真实数值模型进行计算，从而获得目标函数和约束的初始样本。

（3）结合径向基函数与逆向形参数法构建式（11）所示的方程，分别计算出目标函数与约束函数各自代理模型对应的“待选形参数”。

（4）将样本点 ΩX＝｛X1，…，XN｝分为“构建组”｛X1，…，｝和“测试组”{，…，XN}两组样本点，计算目标函数和约束函数代理模型各自对应的最优形参数。

（5）将目标函数代理模型对应的最优形参数与样本点ΩX＝｛X1，…，XN｝结合，从而构建最终的目标函数代理模型；同理，将约束函数各自代理模型对应的最优形参数与样本点 ΩX＝｛X1，…，XN｝结合，从而构建最终的约束函数代理模型。

（6）构建如式（13）所示的汽车乘员约束系统近似优化问题，并采用隔代映射遗传算法（IP-GA）对式（13）所示的汽车乘员约束系统近似优化问题进行求解，获得此近似优化问题的解X（s）。

（7）计算真实目标函数fWIC和约束函数gHIC、gC3ms、gD、gFFL、gFFR在近似优化设计解 X（s）处的值。

（8）计算误差 δmax：

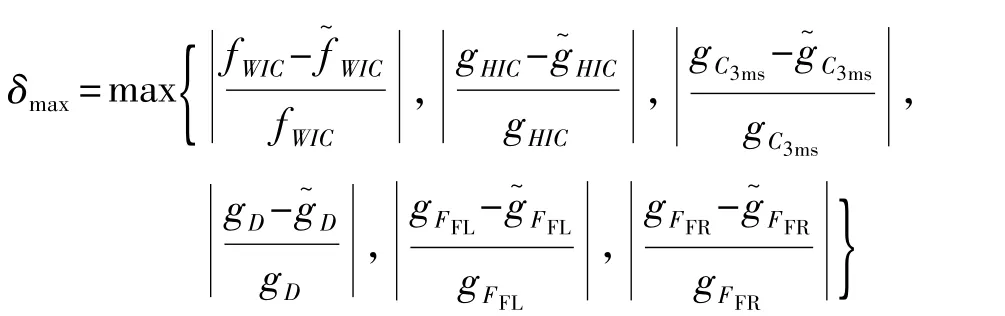
如果 δmax＜emax，则输出优化设计解 X（s），迭代终止；否则，对样本点重新采样，更新样本空间，并返回步骤（2），置 s＝s＋1。

4 优化结果与分析

整个优化过程中，设定许可误差emax＝3%；通过LHD采样，目标函数和约束函数的初始样本点均为30个，其中后续所用到的“构建组”和“测试组”样本点均为15个；优化求解器IP-GA遗传算法的参数设置如下：种群大小N＝5，交叉概率pc＝0.5，变异概率pm＝0.02，迭代次数为100代。

表2为在构建目标函数fWIC的代理模型过程中，使用逆向形参数法计算获得的所有有效形参数。值得说明的是，30个初始样本点理论上应可获得对应的30个待选形参数，但表中只有23个待选形参数，这是因为样本点采样的随机性造成某些样本点在代入式（11）的求解过程中导致矩阵奇异，从而无法获得有效的形参数。根据待选形参数与其对应的测试误差σ，从中挑选误差最小的形参数作为最优形参数。从表2可以看出，9号形参数0.044 0对应的误差只有0.006%，为所有误差值的最小值。因此，选第9号形参数作为目标函数代理模型对应的最优形参数。采用相同的方法，计算约束函数代理模型所对应的最优形参数，其具体结果如下：约束函数的最优形参数为 0.158 0；约束函数和的形参数均为 0.056。

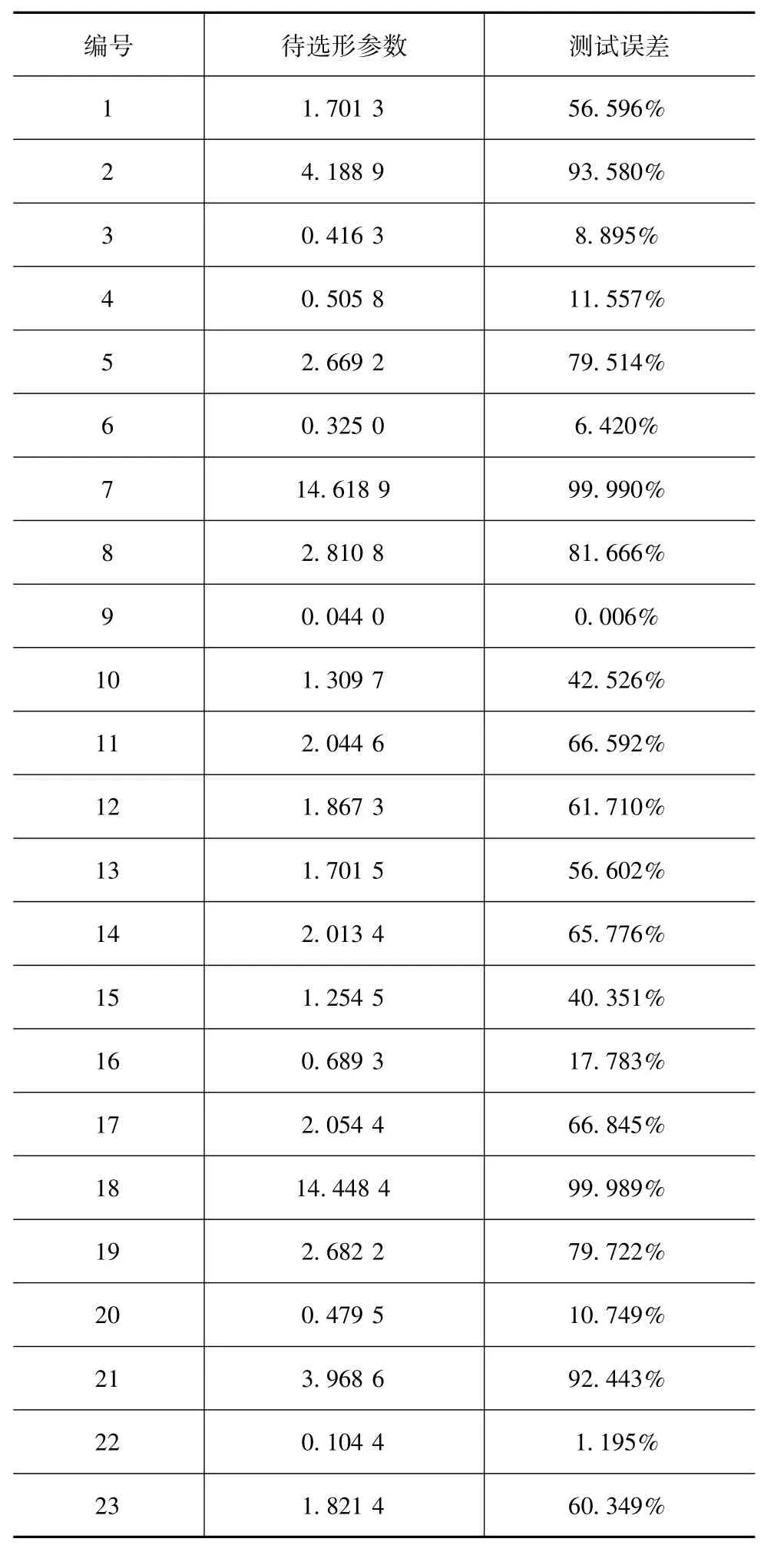
表2 待选形参数与对应的测试误差

当获得目标函数和约束函数代理模型各自对应的最优形参数后，便可与样本点结合而构建最终的代理模型。然后通过IP-GA遗传算法对式（13）所示的近似优化问题进行求解。表3示出近似优化解与真实仿真值的误差对比。由表可知，目标函数和约束函数的优化值与仿真值之间的最大误差仅为1.76%，小于许可误差3%。这说明此时的目标函数和约束函数的代理模型已达到较高精度，且在当前优化设计解（0.868 9，0.007 6，0.930 9，0.000 0）处的各项乘员损伤值均在乘员耐受极限范围内，因此优化结果达到设计要求。

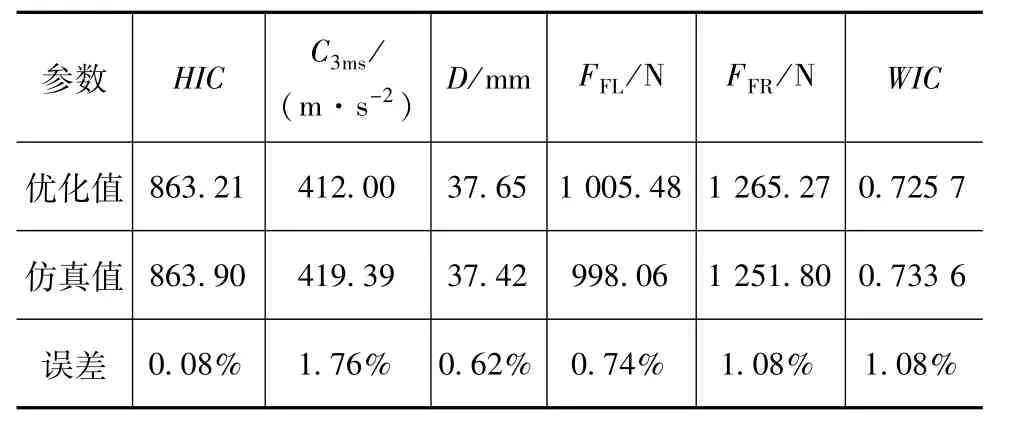
表3 优化值与仿真值对比

表4示出优化前后乘员各项损伤指标值的对比。从表中看出，优化目标 WIC值由优化前的1.022 7降低到优化后的0.733 6，下降了28.27%。头部综合损伤指标HIC值下降显著，由超出许可范围的1 340.30下降到许可范围内的863.90，降低了35.54%。其他几项损伤评价指标也有小幅下降，如胸部3 ms合成加速度、胸部压缩量、左大腿轴向力和右大腿轴向力分别下降了1.40%、1.53%、7.72%和2.30%，均在安全范围内。

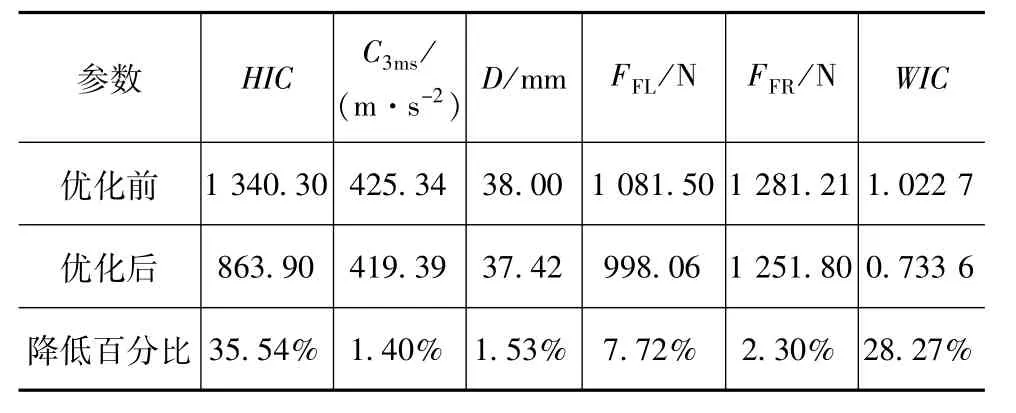
表4 优化前后乘员各项损伤指标值对比

5 结论

（1）构建汽车乘员约束系统100%正面碰撞数值模型，并通过实车碰撞试验验证了数值模型的有效性，以此来研究汽车发生碰撞时乘员身体各部位的动态响应。

（2）为有效保障汽车乘员安全性，提出了一种基于自适应代理模型的汽车乘员约束系统优化设计方法。该方法将径向基函数与逆向形参数法相结合，有效提升了代理模型的精度；并采用IP-GA遗传算法对近似优化问题进行求解。优化结果表明：该方法不仅能改善汽车乘员约束系统的防护性能，还为汽车乘员约束系统的开发与安全性能的加强提供了理论依据，具有一定的工程意义。