以木见林寻规律 自主发现促创新

摘 要：数学教育既要使学生掌握现代生活和学习中所需要的数学知识与技能，更要发挥数学在培养人的思维能力和创造能力方面的不可替代的作用。基于“发现”的自主探究学习，让初中数学课堂有了新的着力点，这种以“学”为本的学习方式避开传统课堂教学中只注重讲解与归纳的被动式学习，让学生主体地位得以进一步提升。

关键词：发现归纳;自主探究;合作创新

中图分类号：G633.6          文献标识码：A     文章編号：1992-7711（2020）11-074-1

教育家第斯多惠指出：“一个坏的教师奉送真理，一个好的教师则教人发现真理。”素质教育和创新教育理念下的教师，决非仅仅是知识的传授者，而应该把自己视为激发、鼓励、促进学生学习和探索的引导者、促进者、咨询者、支持者。教育面对的是人，而不是接收知识的容器。教师所做的，就是要引导学生自己去发现，主动去学习，让学生原有的认知基础上，经过观察、探究、交流，获得新知识或新规律。

一、从“熟视”中提练

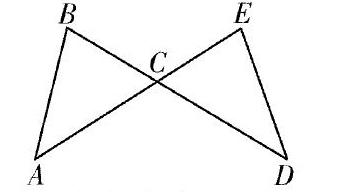
初中几何问题中，有一类常见的基本图形，就是由有一对对顶角的两个三角形所构成的图形。如图，俗称“蝶形图”

（类似于蝴蝶结，也称八字型图，形似阿拉伯数字8），此类图形从三角形到全选三角形，再到四边形、相似三角形，乃至到圆的问题中，几乎都能见到。在经过学生自主探究之后，得出如下结论：（1）构成蝶形图的两个三角形有一个公共顶点，有一对对顶角，所以两个三角形中另外两对角的和相等，并由此进一步发现，另外两对角中如果有一对角相等，则第三对角也一定相等，且这一结论使用广泛;（2）两个三角形可能全等，也可能不全等，如果不全等，则相关结论如（1）所述，如果全等，又可分为两种情况，一种是AB与DE平行，另一种是AB与DE不平行。

或许，学生的发现是浅显的，但这毕竟只是一个开始，正如叶圣陶先生所言：“教师工作的最终目的，无非是培养学生具有各种良好的习惯。”相比较学生学习过程中的“被动发现”甚至“假发现”（老师直接告诉学生），这对他们“学力”的培养还是会起到一定促进作用。

二、在提炼中发现

在老师指导下，学生通过小组合作交流进一步研究发现，“蝶形图”在某一类几何题中出现的机率非常高，这类题目特点是，在等边（腰）三角、正方（矩）形问题中，结合全等证明，几乎无一例外会用到这一基本图形。而且细心的同学发现，这个“蝶形图”在很多时候还是解决问题的关键所在，往往能让人感到“柳暗花明又一村”，令人豁然开朗。

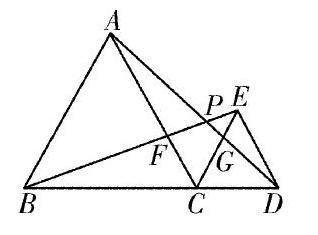
比如，已知如图，C为线段BD上一动点（不与点B、D重合），在BD同侧分别作

等边三角形ABC和等边三角形CDE，AD与BE交于点P，AD与CE交于点G，BE与AC交于点F，求∠APB的度数.初遇这个问题时，不少学生无从下手，引导学生经过仔细观察分析，学生发现了其中的蝶形图APFBC，结合△ACD≌△BCE可知∠CAD=∠CBE，以及对顶角∠AFP=∠BFC，很容易得到∠APF=∠BCF，从而得出问题答案。

三、由发现中创造

根据布鲁纳提倡的发现学习论，强调学生学习的灵活性、主动性和发现性。在教学中要求学生自己观察、探索和实验，发扬创造精神，独立思考，改组材料，自己发现知识、掌握原理原则，这也是所自主探究学习所提倡的重要学习方法。强调通过发现学习来使学生开发智慧潜力，调节和强化学习动机，牢固掌握知识并形成创新的本领。“发现”是导向，是根本，但不是最终目的，在发现中创造，才是学习的终极目标。

通过前面案例的研究，学生已对“蝶形图”形成相对直观且全面，同时又具有一定理性的认识，并且在很多问题中能够具备更加主动发现的意识，为相关问题的分析解决提供了有力的保证。自主探究学习在一定程度上转变了课堂的属性，由“教”转为“学”的课堂，一旦学生的学习主动性得以激发，其所带来的积极效应会引发学生的更多创造力。

有学生在后续探索中提出，对于如图所示的有公共直角顶点的两个等腰直角三角形AOB与A′OB′，无论其中一个三角形如何旋转，总能通过蝶形图ABPB′A′证明到AA′⊥BB′。而还有学生提出，AA′与BB′的夹角大小与两个等腰三角形的顶角有关，等等。总之，自从学生关注到“蝶形图”之后，

在很多几何问题分析时，学生都能有意识地去寻找这样一个基本图形，并以此为突破口，对问题进行更加深入的思考，同时，受此影响，学生在另一个常见基本图形“一线三等角”（K型图）问题的研究上，也更加有效。

四、教后启示思考

基于“发现”的自主探究学习，让初中数学课堂有了新的着力点，这种以“学”为本的学习方式避开传统课堂教学中只注重讲解与归纳的被动式学习，让学生主体地位得以进一步提升。数学教育既要使学生掌握现代生活和学习中所需要的数学知识与技能，更要发挥数学在培养人的思维能力和创造能力方面的不可替代的作用。培养学生的归纳总结能力，也是数学教学中不可或缺的内容之一。以木见林，才能拓展学生视野，有了归纳，才能形成自己见的，再谈创新方有可能。通过“发现”，可以让不同的学生在多层次、全方位的各个角度体验学习的乐趣，使学生以更主动的学习状态，积极投入，热情参与，从而使学生的创新精神和生命潜能得到充分发挥，这也正是初中数学教育的根本追求。

[参考文献]

[1]吴锋.基于“发现”的初中数学导引式合作学习[J].中小学数学，2016（1-2）.

（作者单位：南通市通州区实验中学，江苏 南通226000）