建筑智能设计中的拓扑优化方法综述

钱文亮，黄永，李惠

（哈尔滨工业大学土木工程学院）

1 引言

随着社会经济和文化水平的发展，人们对于建筑结构的美学和力学性能要求越来越高，同时人们也不再单一地要求设计优美的建筑或者性能优越的结构，而是希望美学和力学性能之间实现一个有机的融合[1]。传统的建筑师往往更加注重建筑的美学，考虑更多的是如何设计出更加优雅的建筑，而传统的结构设计师则更加偏重于结构的受力性能设计。拓扑优化方法可以提供一个兼顾建筑美学和力学性能的设计框架，可以将建筑设计师和结构设计师更加紧密地联系在一起。在建筑领域中，拓扑优化一般用于高耸结构的支撑体系设计、桥梁的概念设计以及建筑立面的设计等[2,3]。本文其余的章节安排为：第二章介绍基本的拓扑优化算法，第三章介绍拓扑优化在建筑领域中的具体应用，第四章总结目前拓扑优化方法在建筑领域中应用的现状以及急需解决的问题。

2 拓扑优化算法介绍

拓扑优化方法主要用于在给定荷载和边界条件下寻找设计域中最优的材料布局方案。自从Bendsøe 和Kikuchi在1988 年提出使用均匀化理论进行拓扑优化设计之后[4]，研究者提出了众多用于寻找结构最优化设计的拓扑优化方法，其大致可以分为：①密度方法[5]；②进化方法[6]；③水平集方法[7,8]以及其他方法。密度方法利用和节点或者单元相关的设计变量，然后利用优化算法更新设计变量以达到最小化设计目标的目的。同样的，进化算法也是利用和节点或者单元相关的设计变量，但是不同于密度方法使用优化算法来更新设计变量，进化算法采用启发性原理来更新设计变量，即逐步移除设计域中低效的材料，其概念简单易于被工程师接受，但缺乏严格的数学收敛性证明。进化算法常常又称为“硬杀”方法或者“离散”方法。水平集方法则是通过高一维度的函数来描述优化结构的边界，该方法可以得到显示的边界，从而更好用于结构设计。其他方法还包括相场方法、拓扑描述函数方法以及独立连续映射方法等。目前，随着人工智能的发展，也有一些学者提出了基于深度学习的拓扑优化方法。学者Yonggyun Yu[9]等介绍了一种利用深度神经网络来预测在给定边界和优化参数下拓扑优化结构的方法。其主要做法是，首先获取在不同设计参数下的不同分辨率的拓扑优化训练集，然后使用低分辨率的训练集训练卷积神经网络（CNN），之后再利用模型预测的低分辨率的拓扑优化和高分辨率的真实拓扑优化结构训练生成对抗网络（GAN）来预测更加精细的拓扑结构。

由于密度方法的概念简单，有较为成熟的数学优化算法，同时对于设计域的适应性高以及易于和有限元软件结合，目前大多数商业软件中内置的优化方法都是基于密度方法。下面本文以常见的柔顺度优化问题为例，简单介绍拓扑优化的基本原理。基于最小化柔顺度的拓扑优化问题通常可以用公式(1)进行描述：

目标函数：

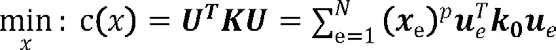
式中：U 和F 为结构整体位移向量和荷载向量，K 为整体刚度矩阵，ue为单元位移向量，k0为初始单元刚度矩阵，xe为单元设计变量，p 为惩罚系数，V0为设计域体积，V(x)为材料体积，volfrac 为体积约束分子。从公式(1)中可以看出来，拓扑优化问题在数学上属于一个优化问题，但是拓扑优化中的优化问题有其本身的特点，比如说设计变量和单元网格精度相关、目标函数值的获取需要调用有限元分析以及目标函数往往只能得到一阶导数等。因此拓扑优化领域中学者们提出了多种用于拓扑优化的优化算法。目前的优化算法有优化准则方法（OC）、序列线性规划方法（SLP） 以及移动渐进算法（MMA）等，而较为常用的是MMA 算法，其核心包含两步：①构造原始优化问题的近似子问题；②使用对偶定理简化近似子问题。由于MMA 算法属于一阶优化算法，因此需要计算目标函数关于设计变量的灵敏度信息，目标函数的灵敏度计算如公式(2)所示：

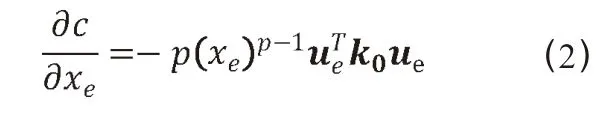
拓扑优化中往往会存在棋盘格现象和网格依赖现象，常常采用启发式的过滤技术[10,11]。学者Lazarov 等将滤波之后的设计变量隐式的定义为Helmholtztype 微分方程的解[11]，如(3)所示：

其中Rmin为滤波半径。同时，使用密度方法进行拓扑优化的时候，往往会产生灰色区域，为了产生清晰的边界往往使用投影技术[12]，关于投影之后的设计变量计算如所示：

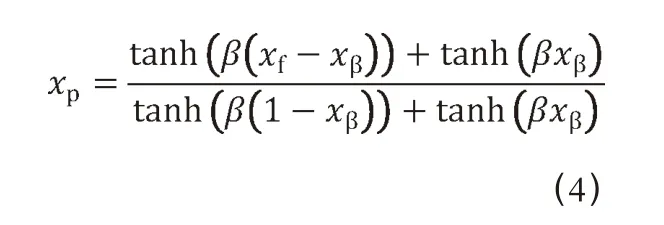
其中是xp投影之后得到的设计变量，xf为滤波之后得到的设计变量，xβ和β 为常数。下面本文用经典的MBB梁优化问题来说明拓扑优化滤波和投影技术的作用。如图 1 (a)所示，MBB 梁长度为6m，高度为1m，跨中的集中荷载为100 kN，材料为钢材，杨氏模量为200×109Pa，泊松比为0.3。

在经过拓扑优化之后，直接得到最优的设计结构(b)，可以看出来该结构边缘呈锯齿状。产生锯齿状的主要原因是由于网格精度问题。因此如果不采用滤波技术，则会导致使用不同的网格精度将得到不同的优化解。为了解决这一问题，使用如公式(3)所示的滤波技术，经过滤波之后得到的结构如(c)所示，此时虽然不再和网格的精度有关，但是优化得到的结构会存在大量的灰色区域。为了解决灰色区域问题，可以使用如公式(4)的投影技术，之后得到的最优结构如(d)。在(d)中可以看出，当使用滤波和投影技术之后既能得到和网格精度无关的优化结构，又能得到清晰的优化结构边界。

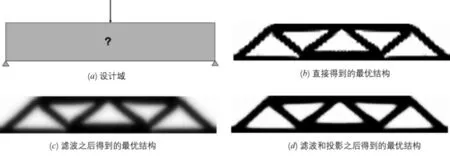
图1 (a) MBB 梁初始设计域 (b) 拓扑结构 (c) 滤波之后得到的优化结构(d) 滤波和投影之后得到的最优结构

3 智能建筑设计中拓扑优化的应用及其算法

本章节主要介绍拓扑优化技术在建筑智能设计领域中的应用。拓扑优化在航空航天、机械和土木工程中具有广泛的应用，在建筑领域中的应用主要包括高耸结构支撑体系的优化、建筑结构立面优化以及其他应用。下面将通过三小节内容分别介绍这些内容。

3.1 高耸结构支撑体系优化

在高耸建筑设计中，设计者主要关心的是在侧向荷载下的整体刚度问题。因此在设计阶段，设计师需要考虑怎样为高耸结构设计出一个更优的支撑体系，去为结构提供更多的刚度或者位移控制，但是传统的支撑结构的设计大多数都是采用对角支撑，角度在45°或者50°以及它们之间变化，这种方法设计出的支撑体系结构形式单一，同时也无法保证是最优的支撑体系， 如图 2(a)和(b)所示的香港中银大厦和美国的约翰汉考克中心的支撑体系是采用的传统支撑结构。而采用拓扑优化技术优化得到的支撑体系受力更加合理，建筑美感也更加强，如图 2(c)和(d)所示的拓扑优化技术得到的高层支撑体系概念设计[1]。

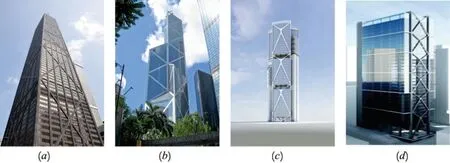
图2 具有支撑结构的现有高耸建筑和使用拓扑优化技术得到地概念设计

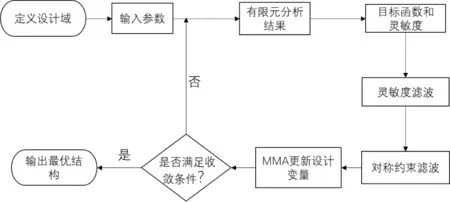
图3 工程对称约束下拓扑优化算法流程图

国内外已有大量的学者对高耸结构支撑体系的优化进行了大量的研究。由于拓扑优化结构得到的优化结构几何复杂，不对称和难于制造的特点，大大增加了优化结构建造的成本，因此大量的学者对于工程可制造约束进行了研究[2]，其中比较简单的可制造约束是对于优化结构加上对称条件，比较常用的做法是采用滤波技术使对称轴两侧的设计变量对称，来实现工程对称约束[13]。下面，本文将通过一个简单的算例来说明支撑体系优化的过程。在算例中，假设支撑结构底端为固定约束。结构的宽为0.1m，高度为0.5m，材料线弹性材料，杨氏模量为210e9Pa，泊松比为0.3，侧面作用等间距集中荷载，其大小为10kN。同时为了解决可制造的问题，在设计中加上对称约束，其算法流程如图 3 所示。

使用拓扑优化算法进行50 次迭代得到的优化结构示意图如图 4 所示：

从图 4 中可以看出来，没有可制造约束的时候，得到的优化结构是不对称的，制造难度较大，很难在工程中应用。而在使用对称约束之后，得到的优化结构更加易于制造。因此为了使得拓扑优化得到结构在实际工程中可以很好的应用，必须要在传统的算法中加上可制造约束。

3.2 建筑立面的美学设计

建筑立面设计是对建筑物外部形状的设计。建筑立面的设计对于结构的美感起到很重要的作用，大多数时候人们对于建筑的第一印象就来自于建筑立面。使用拓扑优化技术进行建筑立面设计，不仅可以有效地承载荷载，还能体现出建筑美感。日本建筑师矶崎利用拓扑优化原理设计了卡塔尔国家会议中心建筑立面，其立面令人印象深刻。卡塔尔国家会议中心的屋顶由拓扑优化得到的混凝土结构支撑，其混凝土支撑结构类似“树形柱”的结构，使得建筑的结构外形十分优雅。学者Mezzadri 等使用拓扑优化技术设计了一系列的自支撑结构[14]，学者Christianse 等利用拓扑技术得到了不同约束条件下的屋顶支撑结构[15]，他们都得到了类似卡塔尔国家会议中心的支撑结构。这种自支撑结构的设计只需要指定好荷载和边界条件，然后通过拓扑优化算法即可实现。本文用一个树形自支撑结构的例子来说明设计流程。在设计树形柱的时候，首先需要定义一个荷载区域，该区域不可设计。算例中的优化结构初始长为10m，高为3.3m，顶端0.3m 高度范围内为荷载区域，不可进行设计，选用弹性材料，杨氏模量为200e9Pa，泊松比为0.3。结构顶端作用均布荷载 -1000 N/m2，结构底部中心0.4m范围内为固定约束。使用拓扑优化算法进行50 次迭代，可以得到上述指定边界条件和荷载作用下的优化结构，其结果如图 5 所示。

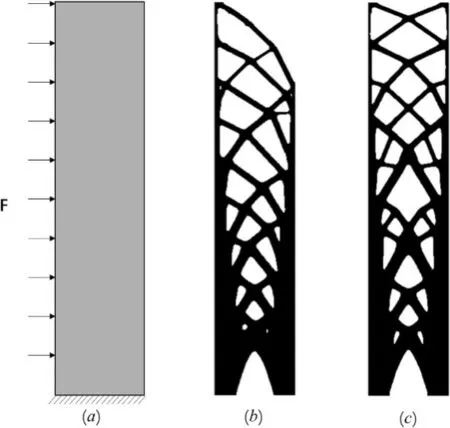
图4 等间距集中荷载作用，a) 设计域b) 无对称约束得到的优化结构 c) 有对称约束得到的优化结构

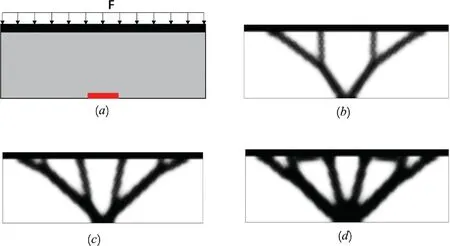
图 5 树形柱的设计

从图 5 中可以看出，当进行拓扑优化的时候，指定不同的体积分数，会得到不同的优化结构。因此在实际的设计中，该方法可用于通过稍微改变输入的参数来生成明显不同的设计。

3.3 其他应用

拓扑优化技术还可以用于其他领域。首先，拓扑优化技术可以用于大尺度的结构优化设计，比如说飞机机翼、大跨度桥梁的设计[16,17]。对于大尺度的结构设计，拓扑优化往往需要使用并行的技术、GPU 编程以及一些先验知识来简化设计域的方法来提高程序运行效率。其次拓扑优化还可以用于动荷载作用下的结构设计[18-21]，比如说地震荷载作用的结构优化设计，可以将动荷载等效为静态荷载或者简谐荷载，也可以将动荷载建模成零均值的平稳白噪声。此外，拓扑优化还可用于多物理场下结构的优化设计[22-25]，比如说可以用来优化流固耦合场中受力的结构。

4 结语

本文首先介绍了拓扑优化问题的数学描述以及用来确保稳定清晰解的滤波和投影技术，其次介绍了拓扑优化技术在建筑智能设计领域中应用。通过拓扑优化技术在建筑智能设计中的例子，可以看出使用拓扑优化框架可以将建筑美学设计和结构设计有机结合在一起，创造出美观且有明显结构工程构件的建筑。

本文在总结文献的基础之上，也对目前拓扑优化技术存在的问题以及未来的研究趋势做出了思考。关于拓扑优化目前存在的问题，本文认为是拓扑优化的计算效率不够高。虽然目前拓扑优化技术已经大量地应用于建筑领域，但是由于拓扑优化问题的设计变量规模大和反复调用有限元程序，使得拓扑优化很难应用在大尺度结构的优化，因此关于未来拓扑优化的研究趋势是怎样提出更加高效快速的优化算法。