巧用反例培养初中生数学思辨能力
李玉琴
摘要:初中生思维领域的跨度以及思维的灵活性、创新性是初中生能否学好数学的关键。然而在很多情况下,学生们的思辨能力没有被很好地开发出来,容易受思维定式的束缚,思域狭窄、思维僵化。在本文中,笔者就培养学生思辨能力的课题提出了自己的看法,在反例应用方面提出了自己的独到见解,希望对初中生思维能力的培养有一定的参考价值。
关键词:初中数学;思维定式;思辨能力;灵活性
中图分类号:G633.6 文献标识码:B文章编号:1672-1578(2020)16-0158-01
小学阶段,数学教学以培养学生们的形象思维和想象力为主,而初中数学知识逻辑性较强,知识的关联性也更为密切。然而,很多学生们的思辨能力较弱,导致解题思维混乱。反例是从不同思维角度来证明命题逻辑思维错误的一种思维方式,有助于辨析命题的真假和概念间的不同。因此,笔者在本文中重点论述了利用反例来培养初中生数学思辨能力的有效途径,希望能够借此拓展学生们的思域的宽广程度,改变思维僵化的窘况,让学生们的数学思维能力得到更好地发展。
1.应用反例强化学生们思维的逻辑性
数学概念和定理主要阐释数学符号、知识模块间的关系,条件性、逻辑性都非常强。一般情况下,初中数学教师会通过朗读、分析或者构建新旧知识之间的联系来正向解析这些概念、公式和定理的内涵。然而,正向解释是从教师的专业角度和成人的思维视角出发,学生们的思维视角和教师的视域存在一定思维差异,因此,学生们对这些概念、定理和公式的适用范围、条件变化后解题思维的变异性和灵活度掌控力不足,容易受教师思路和教材范例所引导的思维定式的影响。但是反例属于逆向思维,能够弥补学生们在理解方面的思维漏洞,让学生们能够从不同角度来看待数学概念、公式及定理的内涵外延,避免学生们条件的遗忘、思维的疏漏,增加理解的清晰度和透彻程度。
例如,5是25的平方根和25的平方根是5这两个命题看似都包含平方根这一概念,但是二者所阐述的逻辑关系并不相同,因此,这两个命题一个为真,一个为假。教师可以通过反例来来提示学生们注意数学语言在表达上所应该具有的严谨性。25的算术平方根是5,它的平方根有两个,一个是5,另一个是-5,因此,5是25的两个平方根中的一个,这种论断在逻辑表达方面没有问题;而25的平方根是5就缺乏表达的严谨度。因为-5也是25的平方根,由此,由条件推断结果的时候得出了不一样的结论,证明这个论断是一个伪命题。
2.借用反例来完善对命题条件的认知
很多情况下,数学命题成立与否要受命题条件的约束,如果能够通过条件推断出相应结论,则命题为真,而如果根据这个条件得出的推论与命题结果相异,则命题为假。因此,学生们对命题条件的认知是否完备,完全可以通过反例来进行验证。
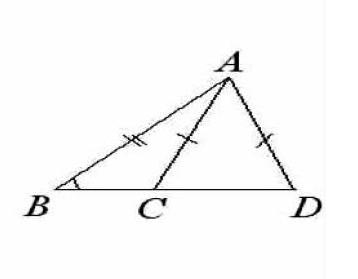
如果正向解析三角形全等的判定方法,教师会要求学生们注意两个疑似全等的三角形在对应角和对应边之间所存在数量对等关系。例如,其中一个判定定理就是“两个三角形的两边及其夹角分别对应相等,那么这两个三角形全等”。正向解析应该是两个疑似全等的三角形之间是否存在两个边数值相等,并且这两个边所形成的夹角是否同时对应相等,如果两个条件同时成立,则这两个三角形全等。这样的解释已经定理所涉及的数学要素间的条件极其逻辑关系阐述得非常清晰。然而在真正的数学解题实战训练过程中,学生们往往看到角或边相等就认为符合条件而忽视角和边对等的前提条件是二者必須具有对应关系。实践证明,笔者正向讲解、正向强调多次,学生们仍然在这方面错误率较高。而笔者把学生们的错题当成反例来讲解,让学生们通过反例纠错的方式来发现此类题的处理原则就会避免学生们对对应条件的忽略。例如,如图
在△ABC与△ABD中,∠ACD=∠ADC,则可以推出AC=AD。那么可知AB=AB,∠B=∠B,AC=AD,但是很明显△ABC与△ABD并不全等。夹角和一边的角绝不是同一概念,不要偷换。这样一来,通过图形对比和逻辑分析,学生们就会对边角边这一三角形全等定理有了更清晰的认知。
3.应用反例来提升学生们的辨析能力
学生们的思辨能力不足,对命题的阐释会产生各种错误的理解,导致命题结果所涵盖内容的扩大或者缩小。应用反例可以有效提升学生们的辨析能力,正确辨析相似度高的概念,明晰其确切适用范围,提升学生对数学知识认知的精确度。
例如,在初中数学知识体系内,学生们学过平面直角坐标系之后,就要辨析锐角和第一象限的角是否是同一概念。当学生们举例400°、430°等角也在第一象限的时候,就会发现,对锐角的定义是大于0°而小于90°的角,而第一象限的角是一个集合,其取值范围为(2kπ,2kπ+π/2),其中k为整数,只有k等于0的时候才是锐角,其他时候都会大于360°.借助这样的反例,学生们对第一象限的角和锐角都有了精准的定义和认知。
综上所述,随着学生们思维认知能力的提升,初中数学知识的抽象性和逻辑性也逐渐增强。学生们要具备良好的辨析能力才会明辨命题的真伪、明晰命题条件的确切含义以及对命题结果的限制作用,并且对相似度高的概念进行正确区分,对A是B正确,但B是A并不一定正确这样的思维认知的辨析尤其有效。反例的使用能够拓展学生们的思维空间,探查到思维意识上的漏洞并指出认知的错误,让学生们的数学思维更为清晰、发散方向更为广阔,辨析能力更为强悍,是教师教学和学生们学习数学知识的得力助手,应该被妥善应用。

