多元化教学应用于高中数学函数解题思路探究
刘 杰
(广东省中山火炬开发区理工学校 528400)
随着新课程改革的逐渐深入,素质教育的大观念对学生综合素质能力的要求也在不断提高.作为高中数学教师,应当要采取措施提高学生数学学习能力,建立新的数学思维模式.多元化教学能够帮助学生开拓思维,提高对数学知识的熟悉度,最终促进学生的数学解题思路,是一种高效的教学方法.
一、高中数学函数解题现状
解题思路主导了高中数学学习的关键,但从当前高中数学函数教学情况来看,大多数学生未能掌握有效的解题思路.原因在于函数学习存在一定的难度,学生学习起来感到吃力,普遍表现出的问题仅仅是停留在对公式的套用上,无法构建知识联系网络,进而灵活的应用并快速形成具体的函数解题思路.而对于教师来说,在引导学生应用多元化的解题思路进行解题时,可以在一定程度上发挥出局部学习的优势,引导自己擅长的知识去解决当前难题,体现出数学的无限可能.
二、多元化在高中数学函数解题思路中的应用方法探究
1.突破传统解题思路,发展逆向性思维
在解题中尝试转化思维,立足于多种角度去审视题目,能够发现其他多种直观易懂的解决方法,探索难题的突破口.
如2017年全国Ⅱ卷理科第21题第二问,常规得零点求导方法并不适用,面对这种情况,可以选择虚设零点、整体替换的方法,从而实现化简变形的目的.
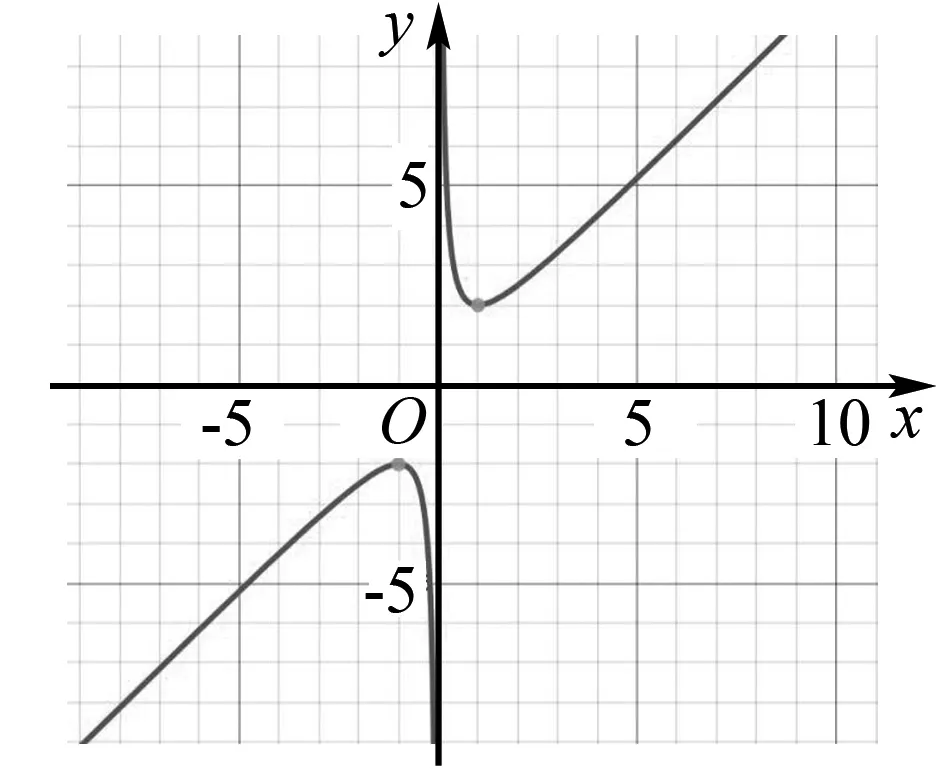
已知函数f(x)=ax2-ax-xlnx且f(x)≥0.证明:f(x)存在唯一的极大值点x0且e-2 ①思路分析: 另一方面,由于f(x0)是f(x)在区间(0,1)内得最大值,故由f(x0)>f(e-1)=e-2. 综上所述,(x)存在唯一的极大值点x0且e-2 2.大胆设想,培养发散性思维能力 方法一:【判别式法】 但函数的另一大特征就是它的图象形式,通过转化为图象,能够清楚、直观地看出结果,这对于数学逻辑思维能力较弱的学生提供了更快速的解题思路. 方法二:【单调性法】 因此x=1时,f(x)有最小值2,即值域为[2,+). 当然,对于数学能力强,知识敏感度高的学生来说,还可以尝试探索更加快速的解题方法. 在教学实践中,教师要从学生角度思考如何有效建立教学模式,帮助梳理知识脉络,发现自己的问题所在.例如,当学生对三角函数公式sin(A+B)=sinAcosB+cosAsinB已经掌握得十分熟练了,但遇到sin24°cos36°+cos24°sin36°这道题目时却不能迅速转换思维,因此,教师可以让学生尝试发现二者之间的联系点,挖掘公式本质内涵,由此使得学生能够掌握公式的普遍性规律,充分理解考点所在,也就能够在此基础上代入更多的方法,最终提高解题效率,有效地解决问题. 综上所诉,多元化解题思路能够帮助学生发散思维,从图象法或者观察法等多种渠道入手,处理复杂而抽象的数学函数问题,帮助能力不同的学生能够采取最适合的解题方法,最终提高学习效率.因此高中数学教师要系统地培养学生多元化解题思维,深入探索数学学习,发展自主学习的习惯.这对于提高学生综合素质能力,快速有效处理实际问题也起到重要的推动作用.


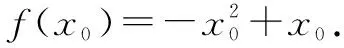

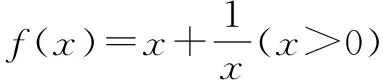
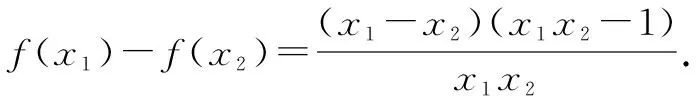
三、转化角色,立足学生角度建立教学模式

