轴瓦弹性变形对固定瓦-可倾瓦组合径向滑动轴承润滑特性的影响

党 超，吕延军，程联社，朱金婷

(1.杨凌职业技术学院机电工程分院, 陕西 杨凌 712100；2.西安理工大学机械与精密仪器工程学院, 陕西 西安 710048；3.重庆公共运输职业学院汽车工程系, 重庆 402247)

0 引言

随着重载设备上滑动轴承的大量使用，轴瓦的弹性变形变得不容忽视，相关研究也日益增多。对于轴瓦变形的计算，国内外学者广泛采用变形矩阵法[1-2]。何芝仙等[3]采用了一种快速近似算法，计算轴瓦弹性变形。Boubendir等[4]在考虑弹性变形条件下，通过求解油膜压力、承载力及偏位角，研究轴承润滑性能。马艳艳等[5]分析了应力偶参数对轴承油膜压力和承载力的影响，结果表明，刚性轴瓦相比弹性轴瓦，最大油膜压力值大，承载力值大，且应力偶参数越大，影响越明显。Okamoto等[6]研究了弹性变形影响下，内燃机连杆轴承的性能变化情况。研究工作者也借助有限元软件对轴瓦变形展开研究[7-10]。随着轴承越来越向高速发展，热因素通过改变润滑油的粘度、密度、轴瓦变形来影响轴承润滑性能变得越来越不能忽视[11-12]。邓玫等[13]分析了同时考虑热效应、变形及轴瓦表面形貌对轴承性能影响。童宝宏等[14]提出了一种分析内燃机主轴承在热变形影响下的静态特性，如油膜厚度、压力、流量和动态特性轴心轨迹的方法。

轴瓦弹性变形改变油膜厚度，导致油膜压力分布变化，油膜压力变化又对轴瓦弹性变形产生影响，因此，轴瓦弹性变形和油膜压力分布相互耦合。以往人们在研究轴瓦弹性变形时，先计算油膜压力，再计算在此压力下的弹性变形，这种算法没有达到真正意义上的耦合。本文提出一种新的耦合算法，采用有限差分法求解油膜压力的Reynolds方程，同时运用3D有限元法求解轴瓦的弹性变形，在油膜压力迭代计算的每一步都计入轴瓦的弹性变形，又在油膜压力的作用下，对轴瓦弹性变形进行求解，两者耦合迭代，分析轴瓦弹性变形对轴承润滑性能的影响。

1 轴瓦弹性变形的计算模型

本文采用3D有限元模型求解轴瓦弹性变形，如图1所示。将轴瓦沿着周向展开为一长方体，其中x指向轴瓦的周向，y指向轴瓦的径向，z指向轴瓦的轴向。轴瓦弹性变形与轴承油膜压力耦合计算流程如图2所示。

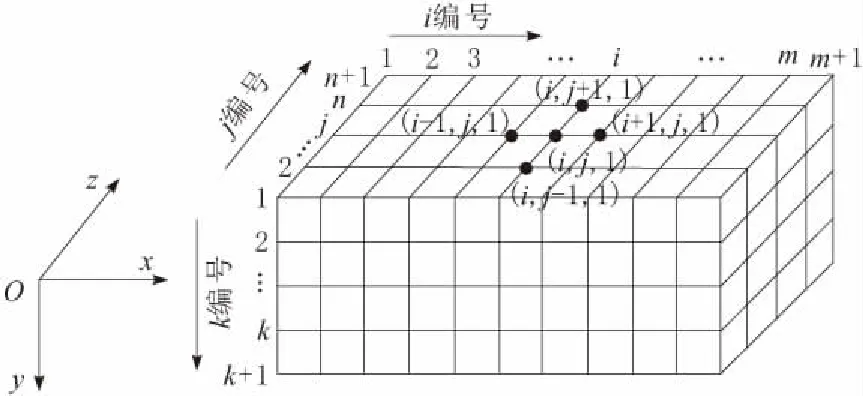
图1 3D有限元模型

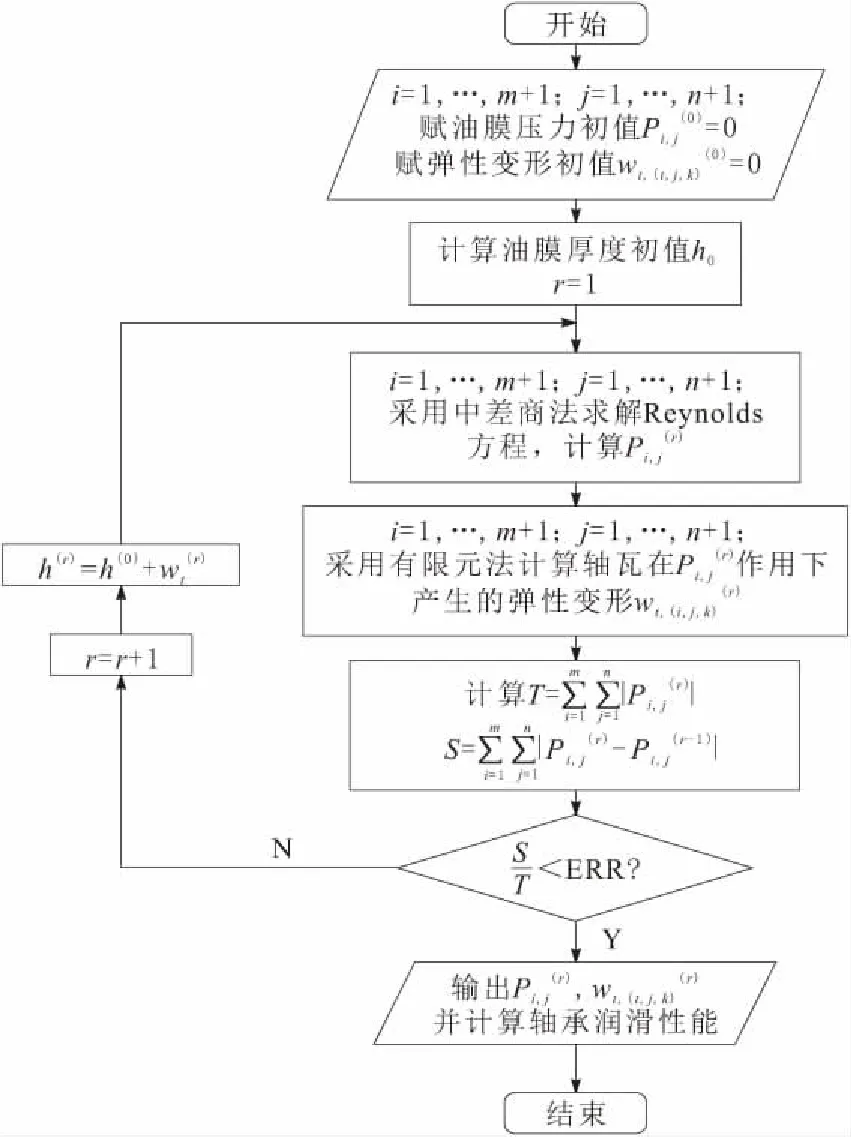
图2 轴瓦弹性变形与轴承油膜压力耦合计算流程

首先通过赋油膜压力初值和瓦块弹性变形初值为零，求解油膜厚度初值，接着采用中差商法求解Reynolds方程，得到油膜压力P，然后计算轴瓦弹性变形，变形又会改变油膜厚度，因此油膜厚度添加修正项wt，如式(1)所示。在此基础上，再计算新油膜厚度下的压力，循环迭代，直到达到收敛精度。

h=h0+wt

(1)

h为考虑轴瓦弹性变形影响下的实际油膜厚度；h0为油膜厚度初值；wt为由于轴瓦弹性变形，油膜厚度增加值，即修正项。

2 油膜压力分布的控制方程

本文以重型燃气轮机上的固定瓦-可倾瓦组合径向滑动轴承为研究对象(1瓦块是固定的，2瓦块和3瓦块是可摆动的)，结构如图3所示。图3中xOby为轴承坐标系，Ob为轴承中心，Oj为轴颈中心，字母下标i为瓦块的编号，R为轴承半径，e为偏心距，θ为偏位角，W为轴承的载荷，φ为从y轴负方向顺时针开始计量的角度。

图3 固定瓦-可倾瓦组合径向滑动轴承结构示意

对于固定瓦-可倾瓦组合径向滑动轴承模型，有量纲Reynolds方程为

(2)

φ和z分别为周向和轴向有量纲坐标；h为有量纲油膜厚度；R为轴承半径。

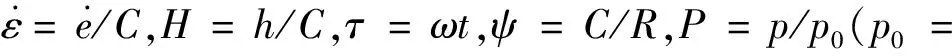
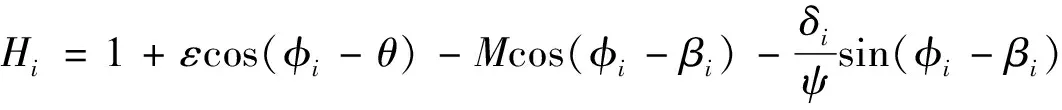
(3)

对于式(3)，采用有限差分法进行求解。

3 数值算例

本文所用的轴承的结构参数如表1所示。

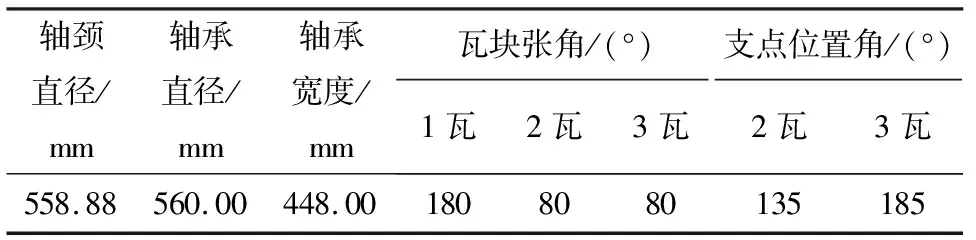
表1 重型燃气轮机组合轴承基本结构参数

轴颈转速为3 000 r/min，宽径比B/D=0.8，润滑油的动力粘度为0.03 Pa·S，间隙比ψ=0.000 5，以下数值算例中的变量，均为无量纲变量。

3.1 轴瓦弹性变形对油膜压力分布的影响

由图3可知，滑动轴承主要由下瓦承担负载，因此本文研究下瓦(2瓦和3瓦)，分析油膜压力如何受轴瓦弹性变形的影响。

当偏心率ε=0.7时，2号轴瓦是否受弹性变形影响下的油膜压力三维分布情况如图4所示，3号轴瓦是否受弹性变形影响下的油膜压力三维分布情况如图5所示。由图4和图5可以看出，轴瓦弹性变形会使油膜压力略变小，且3号轴瓦变化不明显。为了更清楚地分析轴瓦弹性变形如何影响油膜压力，取偏心率ε=0.8，作出2号轴瓦油膜压力沿轴向和周向曲线，分别如图6和图7所示。由图6和图7可以看出，轴瓦弹性变形使油膜压力在轴向和周向的分布变得平缓，且明显变小。

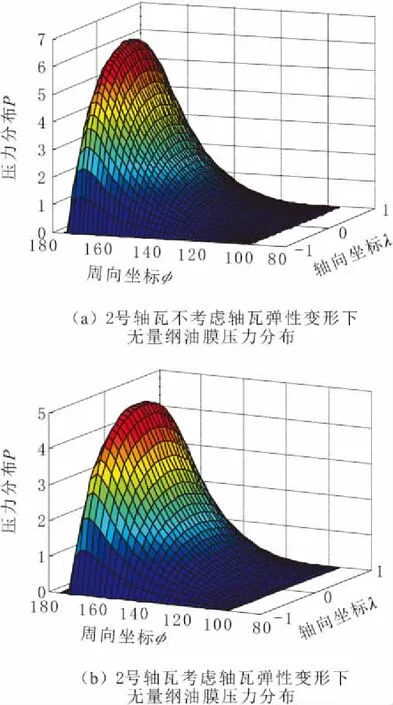
图4 2号轴瓦无量纲油膜压力分布示意

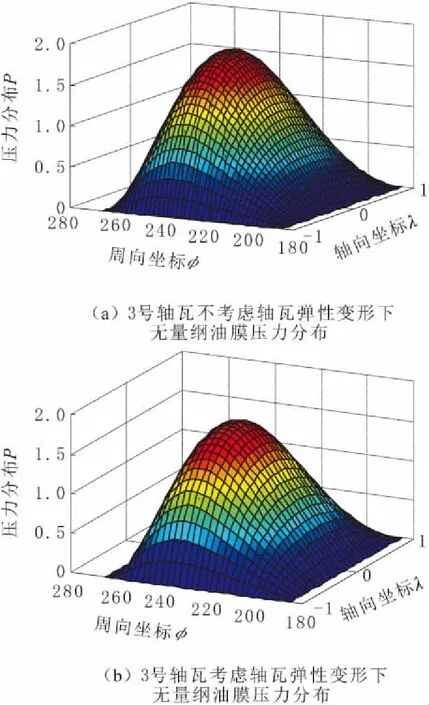
图5 3号轴瓦无量纲油膜压力分布示意

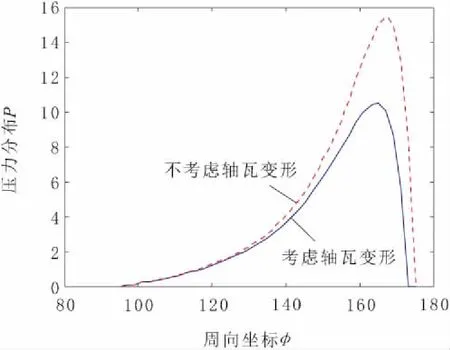
图6 2号轴瓦周向无量纲油膜压力分布P的比较

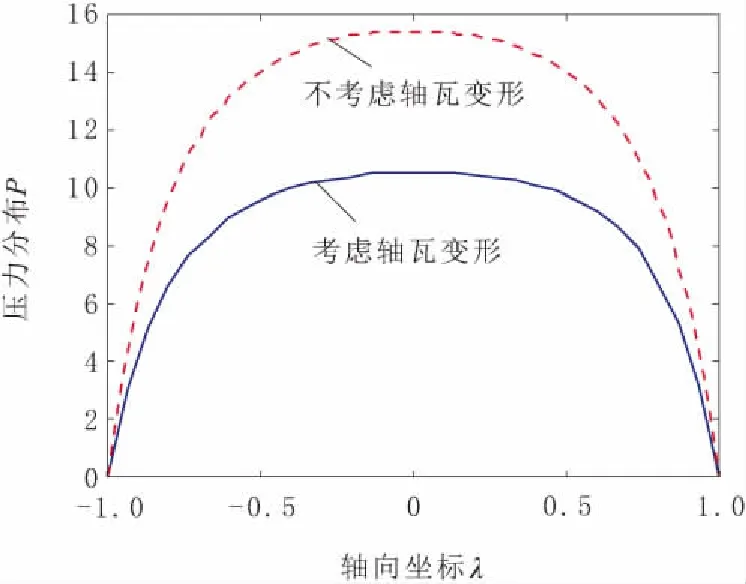
图7 2号轴瓦轴向无量纲油膜压力分布P的比较

3.2 轴瓦弹性变形对油膜承载力的影响

油膜承载力是表征轴承承受负载能力的大小，图8给出了偏心率对承载力的影响曲线。由图8可知，当小偏心率时，轴瓦弹性变形对承载力影响很小，当偏心率变大时，轴瓦弹性变形使承载力减小的越来越大。这表明在大偏心率的条件下，不能忽视轴瓦的弹性变形对油膜承载力的影响。

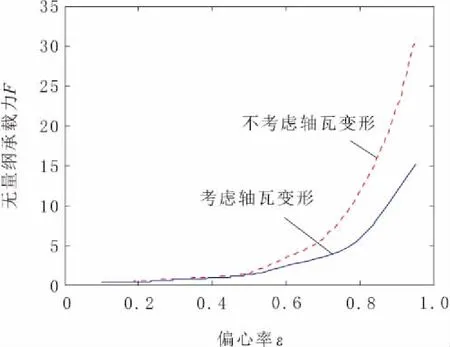
图8 无量纲承载力F随偏心率ε的变化

3.3 轴瓦弹性变形对最小油膜厚度的影响

轴瓦弹性变形通过影响油膜厚度，影响轴承的油膜压力，进而影响轴承润滑特性，2号轴瓦在不同偏心率下的最小油膜厚度如图9所示。

由图9可以得出，当偏心率较小时，轴瓦弹性变形对油膜厚度基本没有影响，当偏心率增大时，考虑和不考虑轴瓦弹性变形的最小油膜差值越来越大。

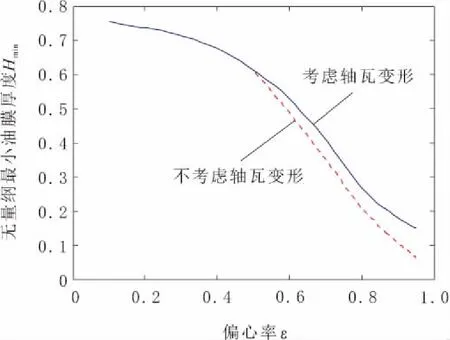
图9 2号轴瓦无量纲最小油膜厚度Hmin随偏心率ε的变化

3.4 轴瓦弹性变形对摩擦阻力的影响

2号轴瓦油膜摩擦阻力随偏心率的变化趋势如图10所示。由图10可以得出，当偏心率低于0.6时，考虑和不考虑轴瓦弹性变形的摩擦阻力基本一致，随着偏心率的增大，两者的差值越来越大，当偏心率ε=0.95时，前者的数值仅为后者的一半左右。

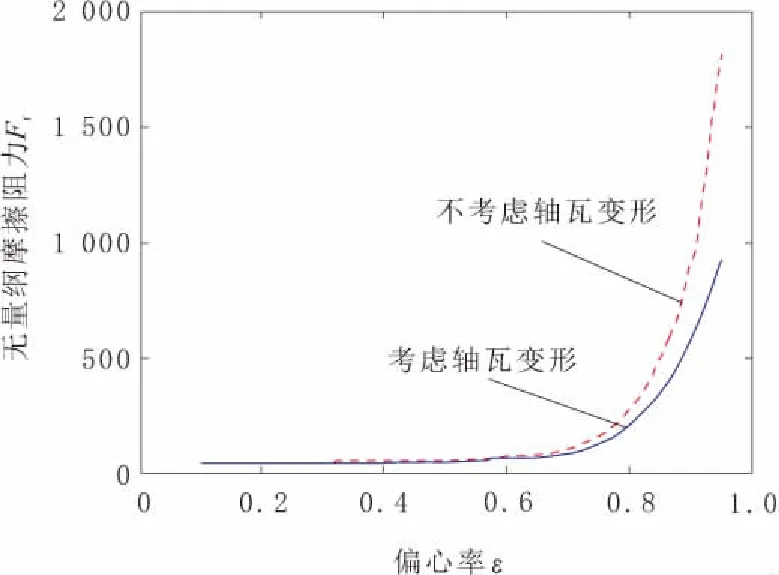
图10 2号轴瓦无量纲摩擦阻力Ft随偏心率ε的变化

3.5 轴瓦弹性变形对轴承端泄量的影响

2号轴瓦在不同偏心率下的的润滑油端泄量如图11所示。

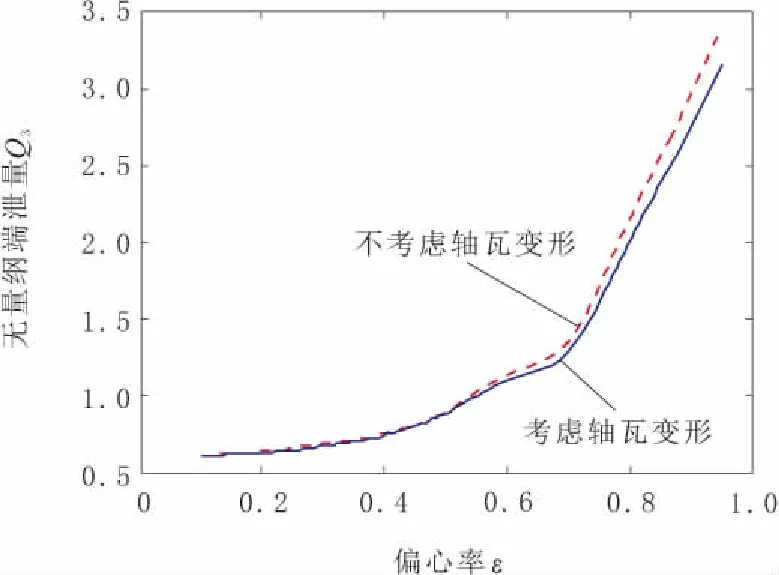
图11 2号轴瓦无量纲端泄量Q3随偏心率ε的变化

由图11可以看出，当偏心率较小时，轴瓦弹性变形对端泄量基本没有影响，随着偏心率的增大，不考虑比考虑轴瓦弹性变形的润滑油端泄量稍大。

4 结束语

采用一种将3D有限元法求解轴瓦弹性变形与有限差分法求解油膜压力耦合的新算法研究了重型燃气轮机上使用的固定瓦-可倾瓦组合径向滑动轴承的润滑性能。通过对比考虑与不考虑轴瓦弹性变形条件下的轴承润滑特性可知，在小偏心率条件下，影响作用不明显，随着偏心率的不断增加，影响越来越大。因此，在偏心率较大时，轴瓦弹性变形的影响作用不能忽视。通过本文的研究，对高速、重载条件下的固定瓦-可倾瓦组合径向滑动轴承的设计提供一定的理论依据。