基于参数稀疏自编码器的旋转机械故障诊断

汪 鹏，何清波

(1.中国科学技术大学精密机械与精密仪器系,安徽 合肥 230026；2.上海交通大学机械与动力工程学院，上海 200240)

0 引言

旋转机械设备在工业中占有重要地位，而滚动轴承、齿轮失效是大部分机械设备故障的主要原因，因此针对旋转机械设备的故障诊断十分重要[1]。尽管已有许多研究人员采用如时频分析，小波分析[2]，随机共振[3]等传统信号分析方法，然而很明显这些方法需要十分专业的信号处理与机械故障诊断知识而且这些专业经验无法直接应对不同场景，因而限制了其应用。随着计算机，集成电路，传感器，机器学习等技术的飞速发展，基于机器学习方法的旋转机械故障诊断得到重视，然而在不同的实际情况下，机器学习方法面临居多挑战。

由于机械设备振动信号的多样性和多变性，因此常见的智能故障诊断方式包括2大步骤：用信号处理方法进行特征提取；使用各种分类器包括支持向量机(SVM)和人工神经网络(ANN)等实现故障识别[4-5]。随着各种智能算法在其他领域取得非凡的成效，智能机械诊断方式也随之发展。Wang等[6]提出了一种深度可分离卷积网络(DSCN)，用于机械的剩余寿命(RUL)预测。Chen等[7]提出了一种融合卷积神经网络和极限学习机的故障诊断方法，在分类精度上优于其他方法。但是以上方法有3个明显的缺陷：信号特征的提取很大程度上依赖于对信号处理技术以及故障诊断专业知识的了解;基于有监督学习方法需要大量有标签数据集，然而机械设备振动信号的价值密度低，且不同设备需要不同的数据集，因此导致可以用于实际工程诊断的数据集匮乏;由特定数据集训练出来的模型不能适应其他故障问题。

由于以上几个问题，无监督特征学习方式得到重视。Thirukovalluru等[8]采用去噪自动编码器从手动特征中提取高级特征，并使用2个分类器来识别机械故障。Lu等[9]研究证明了堆叠降噪自动编码器(SDA)适用于某些包含环境噪声和工作条件波动信号的旋转机械健康状态识别。Shao 等[10]采用最大熵设计自编码器损失函数，增强了从振动信号进行特征学习的能力。Lei 等[11]结合稀疏滤波与softmax回归方式实现无监督特征学习的机械大数据智能故障诊断方法，具有自适应能力，并且减少了人工需求。Zhang等[12]提出通用归一化稀疏滤波(GNSF)的机械故障诊断方法，可以以较少的训练样本获得更高的诊断效率和准确性，并且比以前的方法具有更好的鲁棒性。

自编码器是一种流行的无监督学习模型，已成功应用于各种场景。受稀疏滤波启发，在此,提出了一种基于稀疏自编码器的信号成分分析方法，该方法能够清晰地观察到信号组成成分，通过2个实验来验证该方法是否能够准确判断旋转机械健康状态。

1 自编码器与稀疏滤波

1.1 自编码器

传统自编码器是一种对称的神经网络结构，如图1所示，它由编码器和解码器组成。

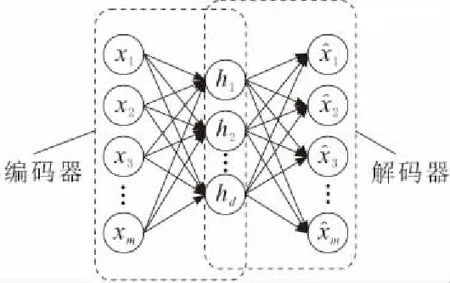
图1 自编码器结构

h=g(W(1)x+b(1))

(1)

(2)

g()为激活函数；W(1)为d×m维权重矩阵；W(2)为m×d维权重矩阵；b(1)为d维偏移向量；b(2)为m维偏移向量。自编码的训练过程旨在优化重构误差，一般MSE被用作自编码的损失函数，即自编码的优化目标如下。

(3)

1.2 稀疏滤波

稀疏滤波是一种有效的无监督特征学习算法,并在机械故障诊断领域的应用有所成效。它可以学习数据集稀疏性分布而不是对数据分布的建模，该算法考虑特征分布满足3个原则：种群稀疏性、生命周期稀疏性和高分散性[13]。种群稀疏意味着每个数据样本仅由几个特征表示，生命周期稀疏表示每个特征仅在少数样本中具有活性，高分散性提高特征泛化能力。简单来说，稀疏滤波是一个2层神经网络，如图2所示。

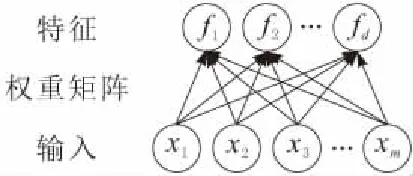
图2 稀疏滤波结构

特征f=Wx，其中x为样本输入，W为权重矩阵。稀疏滤波的任务就是训练网络参数W，使输出特征f能够满足上面提到的3个原则。要达到这个目的，需要对特征矩阵的每一行的2范数归一化再对列进行2范数归一化，最后优化其1范数。如式(4)～式(6)所示：

(4)

(5)

(6)

训练神经网络模型最小化式(6)的值，得到数据集稀疏性分布，此时权重矩阵为稀疏滤波学习到的特征基。

2 参数稀疏自编码器

2.1 理论

参数稀疏自编码器在结构上与传统自编码器无异，但是惩罚函数不一样。为使编码更高效地表示样本数据，找到能将输入向量表示为较少基向量的线性组合模式，在传统自编码器的解码层施加参数约束，使得数据集的编码结果更加有规律可循。

(7)

其中第1项是最小化输入与输出的差异。第2项是参数范数惩罚，最小化解码层参数的1范数，诱导参数稀疏性，目的是限制特征间的相似度。第3项是编码稀疏项，使得：样本特征间稀疏；样本间特征稀疏；特征分布均匀。

下面以一个仿真信号的例子来说明改进型稀疏自编码的作用。

2.2 仿真信号编码

生成仿真信号A和信号B，信号A的频率峰值有11 Hz和49 Hz，信号B的频率峰值有20 Hz和68 Hz，将信号A和信号B经过不同程度的线性叠加得到混合信号，显而易见混合信号的频率峰值有11 Hz、20 Hz、49 Hz和68 Hz，如图3所示。

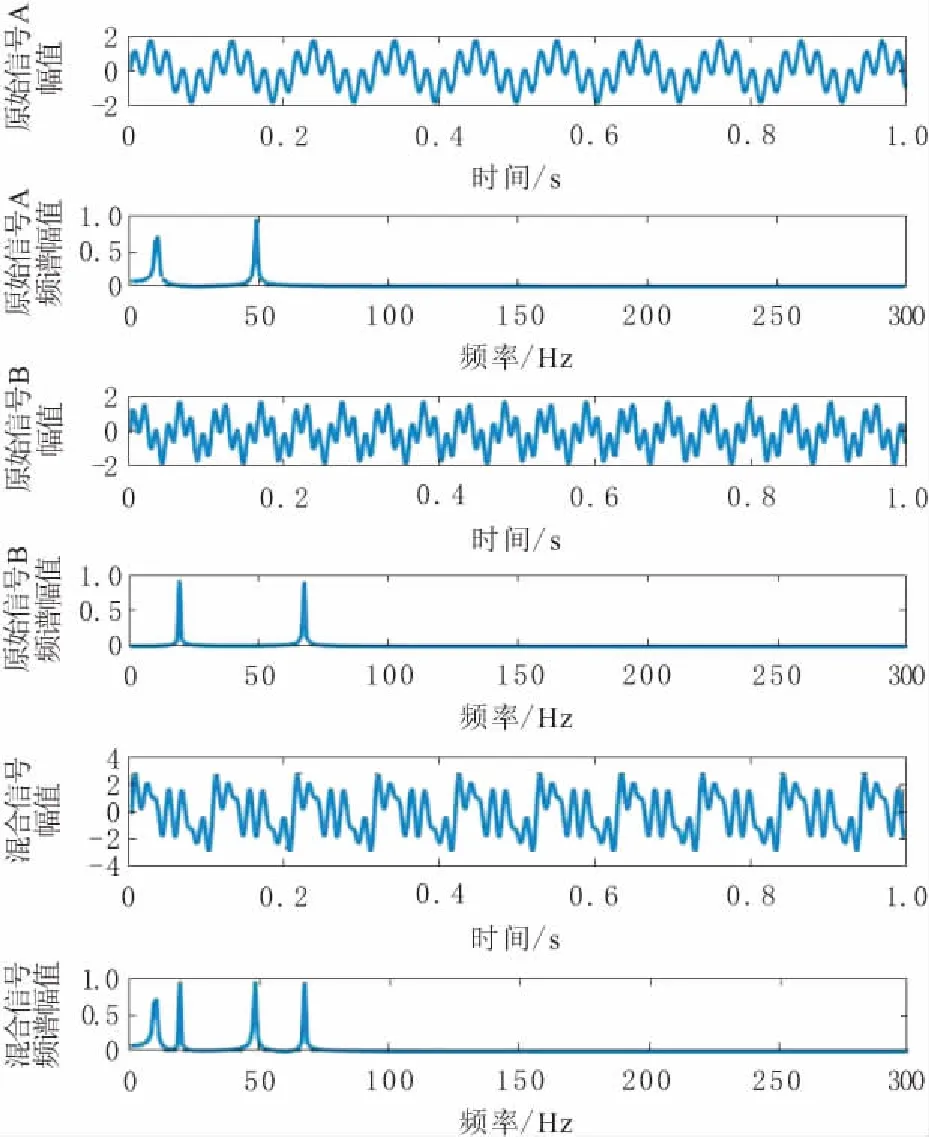
图3 仿真混合信号

由单独信号A、单独信号B以及信号A和信号B经不同程度混合而成的信号各10段共30段组成数据集，作为参数稀疏自编码器输入进行训练，经过参数稀疏自编码器进行编码,结果如图4所示。其中数据序号1～10为信号A，序号11～20为信号B，序号21～30为信号A+B的混合信号。

由图4可以看出，在所有数据的编码结果上只有2个较大的非零编码值，分别是编码3和编码5，信号A独有非零编码5，信号B独有非零编码3，信号A+B则同时具有非零编码3和非零编码5。分别提取这2个编码值进行解码得到解码信号即为分离出的信号，结果如图5所示。分离信号A和信号B及其频谱，由图5可知分离出的信号A和信号B很好地还原了原始信号,而且与原始信号相比在幅度上几乎没有失真。而使用ICA方法分离前述信号得到的结果则与原始信号差异较大而且有较大的幅度失真，如图6所示。可见改进的稀疏自编码器在混合信号特征提取与分离方面有巨大潜力。

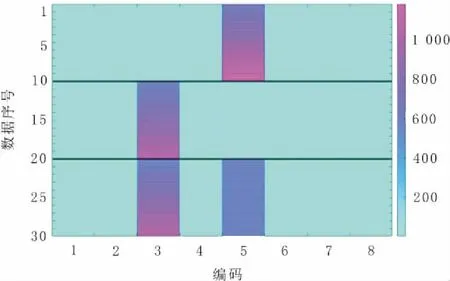
图4 编码结果

图5 稀疏编码分离结果

图6 ICA分离结果

利用参数稀疏自编码器的编码稀疏以及可以分离特征的特性，可以进行无监督信号分类。考虑到机械设备从健康到故障是一个漫长的过程，因此可以预见机械设备振动信号在健康状态的编码只有较少的几个甚至只有1个较大的非零编码值，随着故障特征的出现，编码结果上会出现与健康状态不同的非零编码值，以此为依据判断机械设备的健康状态，从而实现无监督学习的旋转机械故障诊断。接下来通过几个实验验证稀疏自编码器的故障诊断能力。

3 故障诊断实验验证

3.1 轴承实验验证

采用美国Case Western Reserve University(凯斯西储)电气工程实验室的滚动轴承故障模拟实验数据集[14]，其实验装置台如图7所示。包括1个2马力的电动机，1个扭矩传感器，1个功率测试计。待检测的轴承支撑着电动机的转轴，驱动端轴承型号为SKF6205，轴承参数如表1所示，其内圈故障频率为5.415 2倍转频，外圈故障频率为3.584 8倍转频。驱动端轴承故障采样频率为12 kHz 和48 kHz。功率和转速是通过扭矩传感器/译码器测得手动记录得到。实验时的转速包括1 730 r/min，1 750 r/min，1 772 r/min及1 797 r/min。

图7 凯西西储滚动轴承故障模拟实验台

表1 轴承参数 mm

选取内圈故障、外圈故障、正常轴承信号以及将内圈故障外圈故障信号进行混合得到额外一组信号，切片处理并计算包络谱得到共170组数据作为自编码器输入。使用自适应矩估计方法最小化惩罚函数训练自编码器模型，最后得到的编码结果如图8所示。

图8 轴承信号编码结果及对应解码参数

由图8可以看出，所有数据的编码均在编码8上有较大的非零值，这是因为所有信号都一定具有轴承转频等系统固有频率特征。因而健康轴承信号在8维的编码上表现为仅有一个较大的非零编码值编码8，而故障轴承信号在编码上具有一个较大的与健康信号不同的非零编码特征值，轴承内圈故障信号除了编码8较大外还有一个较大的非零编码2，轴承外圈故障信号独有一个较大非零编码3。由此可以认为编码2代表轴承内圈故障特征，编码3代表轴承外圈故障特征。可见通过较大的非零编码值判断轴承健康状态是可行的。

3.2 齿轮箱实验验证

采用东南大学动态模拟器收集的齿轮箱实验数据集[15]，其中包含轴承数据和齿轮数据，每组数据包含4类故障数据与1类健康数据。齿轮数据集包含以下5类健康状态：齿缺口、齿缺失、根部裂纹、表面磨损和正常状态。轴承数据集包含5类健康状态：滚子故障、内圈故障、外圈故障、内外圈都故障和正常状态。

对原始信号进行分割，每类健康状态取20段信号共计100段信号，每段信号长度为600，计算其包络谱作为改进稀疏编码器的输入。数据序号与对应健康状态如表2所示。

表2 数据分布

编码器结构和前面轴承实验结构一致，编码结果纬度为8。编码结果分别如图9和图10所示。每种健康状态都具有其独特的编码形式。通过编码结果中的较大非零编码分布即可轻易分辨出数据的健康状态。

由图9可知，对于实验中轴承数据集的编码，所有数据均有较大非零编码6，健康轴承几乎仅有唯一一个非零编码6；对于滚子故障、内圈故障、外圈故障数据除了共有非零编码6外，还各自独有一个非零编码分别是3、8、4；而对于内外圈都故障的数据则同时具有非零编码4、8。由图10可知，对于齿轮数据集的编码，所有数据都有一个非零编码5，除此之外不同健康状态数据独有一个额外非零编码，齿缺口、健康、齿缺失、根部裂纹、表面磨损5类齿轮数据独有非零编码分别为4、2、3、8、6。由此可见对于不同健康状态数据其编码差异性十分明显，因此所提出的方法可以区分出该实验数据集的几种不同故障状态，并且由于编码器本身可以学习信号特征成分，因此对于有混合故障的数据也有很好的识别性。

图9 轴承数据编码结果

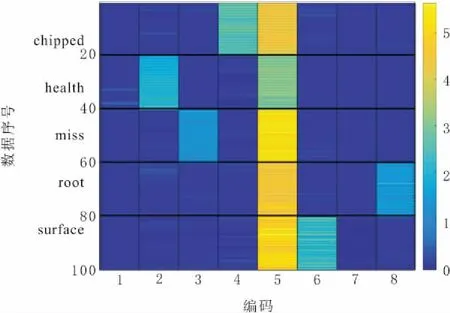
图10 齿轮数据编码结果

4 结束语

提出的改进型稀疏自编码器能够在大量数据集中学习信号组成成分提取不同信号间的异同特征并通过编码形式表现出来，通过实验验证表明：不同种类的故障信号会有不同的非零编码，通过不同信号编码结果的差异性来判断旋转机械健康状态是可行的。在实际生产中，健康数据总是易获取的，通过比对目标数据与健康数据编码差异来判断旋转机械的健康状态的方法具有较强的可用性。