浅海主动声呐混响干涉结构特性及增强方法

唐浩 王方勇

（声纳技术重点实验室 第七一五研究所，杭州，310023）

海洋信道中传播的声信号受色散效应影响，在空频域具有明暗相间的干涉结构。随着实验技术的提高和声场理论的发展，已通过实验观测到海洋声场的干涉结构并通过理论解释其产生机理。干涉结构最早在被动声呐的距离-频率域被发现，由于其包含了信道和目标的参数信息，并且自身可用波导不变量β简洁地刻画[1]，因此众多学者开展了基于被动声呐干涉结构的水声物理和水声信号处理方面的研究，主要包括海底参数反演、海洋参数检测和声源定位等[2-5]。

近年来，Goldhahn[6]和李风华[7-8]分别利用不同的理论推导出主动声呐混响信号在时间-频率平面同样具有干涉结构，并且理论预测结果与海试实验结果能够较好地吻合。随后，不同学者利用主动声呐接收信号的干涉结构，提出了一些目标探测和跟踪方法。Goldhahn提出了一种基于混响干涉条纹的恒虚警检测方法，其性能优于常规距离平滑恒虚警检测方法。Quijano和Zurk[9-11]等研究了主动声呐目标回波的空频干涉结构，通过在状态向量中增加从干涉条纹中提取的动态频率，提出一种基于干涉条纹的改进扩展卡尔曼滤波方法，跟踪结果优于常规扩展卡尔曼滤波。郭国强[12]将海底混响的干涉结构和谱相减的思想结合，提出了一种混响预测对消方法用于提高主动声呐的目标检测能力。

以上方法性能的优劣取决于清晰混响干涉结构的获取，本文根据主动声呐混响信号的特点，结合时频分析获取干涉条纹的方法，提出一种基于变窗长短时傅立叶变换的干涉条纹增强算法。通过该方法所获得的混响干涉结构更加清晰，有利于提高基于干涉结构的目标探测和跟踪方法的性能。

1 理论模型

1.1 基于简正波理论的主动声呐混响模型

海底混响是浅海混响的主要组成部分，图1为海底混响示意图，S为收发合置的主动声呐，小黑点为面积微元内的散射体，混响信号可表示为面积微元dA内所有散射体回波信号之和，

图1 海底混响示意图

利用分离变量法求解亥姆霍兹方程，声压函数可以表示成一系列简正波的和，假定时间因子为exp(-jωt)，单程传播远场声压可表示为

式中，zs和zr分别为发射元和接收元的深度，km和ψm分别为第m阶模态的水平波数和本征函数，，后文公式中省略此系数。主动声呐接收的回波信号为双程声传播信号，利用式（2）结果和互易原理，深度zs处的收发合置声呐接收到(r,zi)处的散射体回波信号为

式中，Smn为第m号入射简正波激发第n号散射简正波的单元散射强度，采用Lambert海底散射模型，，μ为海底散射系数。

当发射信号的频域为S()ω时，利用傅里叶逆变换得到单个散射体散射回波的时域，再带入式（1），可得到主动声呐接收的海底混响，

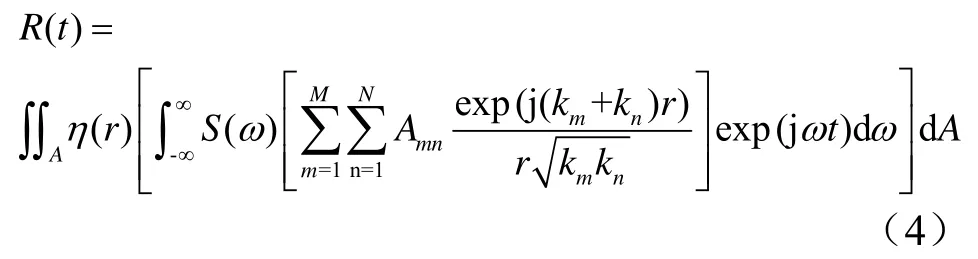
本研究采用问卷调查法，通过方便抽样，对广东某高校的创新创业实践教学体系进行调查。问卷分为学生问卷和教师问卷两类，共发放学生问卷400份，回收381份，回收率为95.3%。教师问卷主要对象为创新创业授课教师，共发放60份，回收53份，回收率为88.3%。问卷含人口学资料、25道选择题、1道主观附加题。问卷主要聚焦对目前高校创新创业教育课程体系的态度和教师创新创业教学能力评价。从师生两个角度的互评中揭示创新创业教育的现实并且根据数据分析发现教学体系存在的不足。

1.2 主动声呐混响干涉结构

根据式（3）可以得到任意散射体回波的声强：

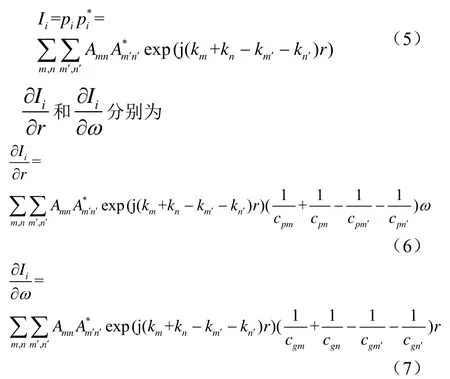
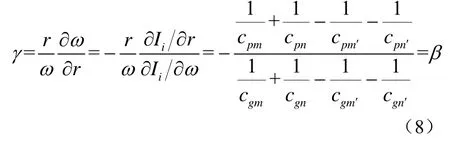
2 混响干涉结构增强方法

推导式（8）所示的混响波导不变量时，直接利用式（3）所示的任意距离处散射体回波的频域公式。在实际信号处理中，需要对混响时域信号进行时频分析，一般采用短时傅立叶变换（Short Time Fourier Transform，STFT）求得，因此STFT采用的窗函数的非零区间将影响所提取的干涉结构的清晰度。对式（4）所示的时域混响信号进行STFT：

其中

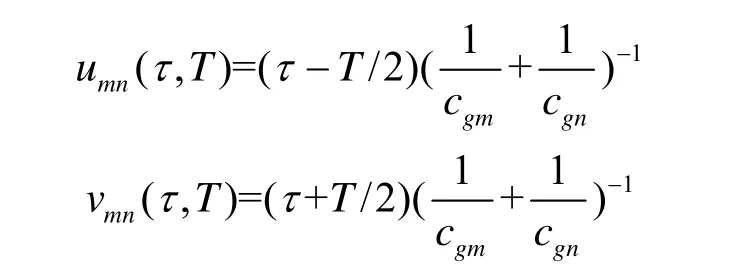
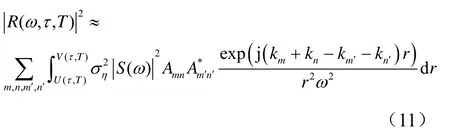
式（12）中ω、τ、T只出现于积分外和积分上下限中，若ω′=αβ ω，τ′=ατ，T′=αT，α为正实数，积分上下限不变，可得

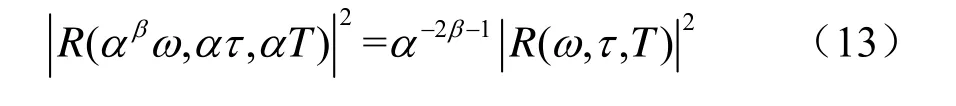
式（13）表示，混响序列经过以时刻τ为中心、T为窗长的STFT得到的声强，近似等于其经过以时刻ατ为中心、Tα为窗长的STFT得到的声强，即STFT采用的窗长随窗中心时刻等比例增加时，可以对得到的干涉条纹进行增强。

3 仿真分析

利用式（3）可仿真混响在ω-r域的干涉结构，仿真一采用的海洋信道参数为：Pekeris均匀波导，等声速剖面，声速1500 m/s，海深100 m，海底密度1.77 g/cm3，海底声速1637 m/s，海底衰减系数1.7 dB/λ。声呐和混响位置参数：收发合置声呐深度50 m，海底混响距离2.5～12 km。根据上述模型及参数，收发合置主动声呐的混响信号在ω-r域的干涉结构如图2所示，不同颜色代表不同强度的声强（下同），干涉条纹与单向传播相同，仿真结果与理论公式推导的结论一致。

图2 混响ω-r域干涉结构

根据已建立的基于简正波理论的主动声呐混响模型，利用与上述参数相同的信道参数及声呐位置参数，当发射信号频率为 50～150 Hz、脉宽 1 s的双曲调频信号时，接收到的混响序列仿真结果如图3所示，图4为发射信号及混响序列的频谱。

图3 混响时间序列仿真结果

图4 发射信号及混响序列的频谱

利用STFT提取图2所示混响序列的干涉结构，图5为变窗长STFT和固定窗长STFT的提取结果。为突出干涉结构，下图为上图增加白色辅助线的效果。图5（a）窗长的选择与窗中心距离成正比，最小窗长为0.08 s，最大窗长0.58 s，重叠率为50%；图5（b）的窗长与窗中心距离无关，统一采用0.2 s，重叠率为50%。对比发现，近距离处（3～7 km），变窗长与固定窗长的处理结果差别不大，但远距离处（7～11 km），变窗长所提取的干涉结构比固定窗长更加清晰，利用Hough变换处理图5提取的干涉结构，（a）得到的 Hough矩阵的最大值比（b）大1.4%，说明采用变窗长方法增强了提取的干涉结构，条纹的直线信息更加突出。

图5 混响仿真一干涉结构提取结果

仿真二的声速剖面采用典型浅海声速，20～35 m存在跃变层，如图6所示，其他参数与仿真一相同。同样利用变窗长和固定窗长STFT的提取干涉结构，变窗长STFT的窗长的选择与窗中心距离成正比，最小窗长为0.08 s，最大窗长0.58 s，重叠率为50%；固定窗长STFT的窗长与窗中心距离无关，统一采用0.2 s，重叠率为50%，结果如图7所示。

图6 仿真二的声速剖面

图7 混响仿真二干涉结构提取结果

观察发现非等声速水文条件下，混响干涉结构受水文影响变弱，但本文提出的变窗长STFT方法同样在远距离处具有增强效果，利用Hough变换处理图7提取的干涉结构，（a）的Hough矩阵最大值比（b）大0.9%。

4 实验数据分析

利用本文提出的基于变窗长STFT的干涉条纹增强算法和固定窗长STFT提取方法分别处理某次海试采集的混响数据（发射信号为1.5～2.0 kHz的双曲调频信号），提取结果如图8所示。图8（a）窗长的选择与窗中心距离成正比，最小窗长为0.04 s，最大窗长0.21 s，重叠率为50%；图8（b）的窗长与窗中心距离无关，统一采用0.05 s，重叠率为50%，为突出干涉结构，下图为上图增加白色辅助线的效果。两种提取方法处理海试数据的效果与处理仿真数据的效果相同，近距离处二者相差不大；远距离处变窗长方法所提取的干涉结构更加清晰。利用Hough变换处理图8提取的干涉结构，分析其中的直线信息，（a）的Hough矩阵的最大值比（b）大1.1%，说明采用变窗长方法增强了提取的干涉结构，条纹的直线信息更加突出。

图8 混响实验数据干涉结构提取结果

5 结论

主动声呐混响信号具有干涉结构，实际处理混响信号时，需要对时域信号进行时频分析获取干涉条纹。本文提出的基于变窗长STFT的干涉条纹增强算法，充分利用主动声呐具有明确时间信息的优势，采用的窗长随窗中心时刻等比例增加。变窗长的处理方法所提取的混响干涉结构更加清晰，尤其是远距离处的条纹增强效果更明显。本文主要通过窗长的改变增强提取的混响干涉结构，为进一步提高干涉条纹清晰度，可尝试利用不同的窗函数或者其他时频分析方法。