基于改进粒子群算法的变电站巡视路径问题研究

钟成

（广西电网有限责任公司北海供电局，广西 北海 536000）

0 前言

随着技术的进步，变电站智能机器人巡视受到了重视，巡视路径的优化对于提高巡视效率有着重要的作用。利用机器人巡视变电站，可以大幅减轻巡维人员工作压力，解放劳动力，使巡维人员从事更加专业的工作，对于化解电力设备数量不断增长与巡维人员不足之间的矛盾有重要意义。优化变电站设备巡视路径是降低智能巡视机器人能耗，提高机器人效率的有效手段。变电站设备巡视路径优化问题可以描述为：给定l个设备间隔以及各设备间隔的平面位置坐标，求解一条经过各设备间隔的最短路径。其数学模型为：假设l个设备间隔的集合G={G1,G2,G3...,Gl}，且每两个设备间隔的距离为d(Gi,Gj)，要求解一条Hamilton回路，使的值最小。这是一个典型的优化问题，随着问题规模的扩大（设备间隔数目增加），该问题的求解结果会呈现指数级增加，造成求解过程越来越复杂，所需的计算时间也越来越长，因此该问题属于组合优化NP问题（Non-Deterministic Polynomial Problems ，存在多项式算法能够解决的非决定性问题）[1]。若采用传统的算法，例如穷举搜索法、线性规划法，是难以实现的，所以需要找到更优化的算法来求解此问题。

粒子群优化算法（Particle Swarm Optimization，PSO）是一种进化计算技术，1995 年由Eberhart 博士和Kennedy 博士提出，源于对鸟群捕食的行为研究[2]。该算法最初是受到飞鸟集群活动的规律性启发，进而利用群体智能建立的一个简化模型。粒子群算法是建立在对动物集群行为观察的基础上，利用集群中个体对信息的共享，使整个集群的运动规律在求解空间中产生有规则可循的演化过程，进而求出最优解。

1 粒子群算法基本原理

粒子群优化算法对鸟群的捕食行为进行模拟，设想这样一个场景：一群鸟在某区域内随机搜索食物，但在该区域里有且仅有一块食物，所有的鸟都不知道食物具体位置，但他们知道当前的位置离食物还有多远，因此找到食物的最优策略是搜寻目前离食物最近的鸟的周围区域，从而获悉食物位置[3]。PSO算法中每个粒子代表问题的潜在解，并且每个粒子对应于由适应度函数确定的适应度值。粒子的速度决定了粒子移动的方向和距离，速度随自身及其他粒子的移动经验进行动态调整，进而实现个体在可解空间中的寻优。

假定在一个m维的空间中，有n个粒子组成粒子群X={X1,X2,X3...,Xn}，其中第i个粒子的位置向量为Xi={Xi1,Xi2,...,Xin}，速度向量为Vi={Vi1,Vi2,...,Vin}，该粒子在m维空间移动过程中历经的最优位置为Pi={Pi1,Pi2,...,Pin}。将全部粒子经过的最优位置用PG表示，则PG={PG1,PG2,...,PGn}。粒子在每次迭代后的速度与位置评价函数分别用下列式（1）、式（2）表示：

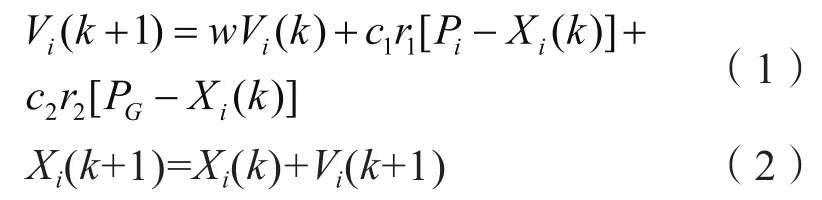
在式中k为迭代次数，w是惯性权重，c1、c2指加速因子，r1、r2为在区间[0,1]内服从均匀分布的随机数。式（1）中的wVi(k)为动量部分，为粒子提供一个初始动量，使之可根据初速度进行惯性运动；c1r1[Pi－Xi(k)]称为认知部分，表示粒子自身的记忆行为，激发粒子向自身曾发现的最优位置移动；c2r2[PG－Xi(k)]为社会部分，表示粒子间的相互影响，引导其他粒子向粒子群的最优解移动[4-9]。三部分的平衡约束决定了PSO算法的性能。在迭代计算的过程中，为了防止粒子超速盲目搜索，还要对粒子的速度加以限制，一般将粒子的位置限制在区间[－Ximax,Ximax]内。

2 改进策略

由于传统的粒子群算法存在早熟收敛于局部最优解和收速度敛较慢的问题[10-13]，本文提出了以下改进：

2.1 进化变异粒子个体

变异操作是增加种群多样性的重要方法，适当的变异既可以使种群多样化，又能提高局部区域探索能力。本文引入进化变异算子，当多样性低时，增加变异因素，使算法探索更广阔的空间；当多样性较强时，削弱变异因素，使算法在小范围内精确求解。

用Sij表示粒子Xi、Xj的相似度：

式中m表示粒子空间维数。

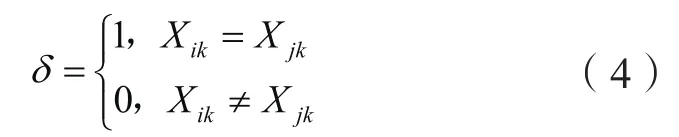
当Xik=Xjk时，表示粒子Xi与Xj在第k个位置的值相等。Sij∈[0,1]，若Sij=1Sij=[0,1]，则表示Xi、Xj完全相同。

定义第i个粒子的多样性Di：

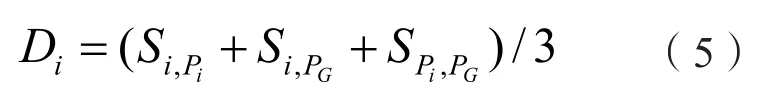
式（5）中，Pi为第i个粒子的最优解，PG为全部粒子的最优解。

将粒子种群多样性定义为单个粒子多样性的平均值：

当D≤0.3时，执行该变异进化，并采用顺序交换法将粒子Xi={Xi1,Xi2,...,Xin}中随机产生的Xij、Xik两个变异位置进行交换，得到新粒子Xi=(Xi1,Xi2,...,Xij-1,...,Xik-1,Xij,Xik+1,...,XiS)。

2.2 自适应调整惯性权重

在粒子群优化的过程中，按照适应度的大小对当前的粒子群X=(X1,X2,...,Xn)进行降序排序，并相应形成一个排好序的新粒子群Y=(Y1,Y2,...,Yn)，令fi为种群规模为n的粒子群中，第i个粒子的适应度，Yi∈{f1,f2,...,fn}，1≤i≤n。由于新粒子群中排列第一的粒子适应度最强，因此将其称之为最优粒子，相应的把新粒子群中第i个粒子与最优粒子的距离称为最优粒子距di。隶属函数是模糊集合论中的一个基础概念，是模糊集合理论与方法具体应用的基石。因此如何建立某个模糊概念的较为合适的隶属函数，是用模糊集合的方法能否较好的解决问题的关键。本文通过引入最优粒子距的概念，隶属函数u(di,x)的表达式如下：

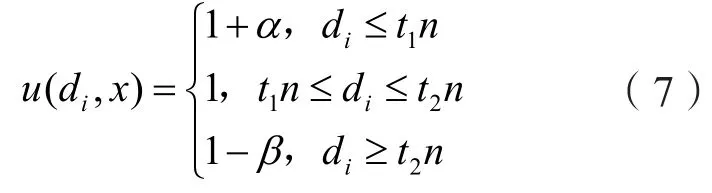
式（7） 中，n为 粒 子 群 规 模，t1、t2为控制参数，α、β为调整系数，并且满足条件t1≤t2≤1，α≥0，β≥0。

通过上述隶属函数的映射关系，可以知道个体粒子在粒子群中的隶属度，根据每个粒子的隶属度，可以建立如下惯性权重自适应调整函数w(i,x)：

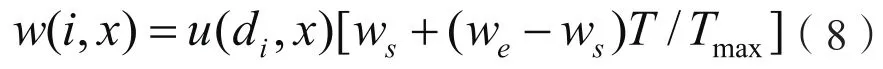
式（8）中T为当前迭代次数，Tmax为最大迭代次数，ws、we分别表示惯性权重w的初始值和结束值。

3 仿真研究

本文应用的实例为某500 kV变电站，根据该站的电气总平面布置图构建平面直角坐标系，并列出该站需巡视的52个设备间隔的平面直角坐标值。采用MATLAB R2013a进行仿真测试，本改进粒子群算法的参数设置如下：加速因子c1=1.4，c2=1.6；控制参数t1=0.4，t2=0.6；调整系数α=3，β=2。

表1 改进粒子群算法求解变电站设备巡视路径问题结果

表1统计了采用本文提出的改进粒子群算法，求解变电站设备巡视路径优化问题时，分别于10次、50次、100次以及200次迭代后得出的最优解情况。由此可见，随着迭代次数的增加，最短巡视路径的路程也逐渐减少，求解结果收敛于最优。

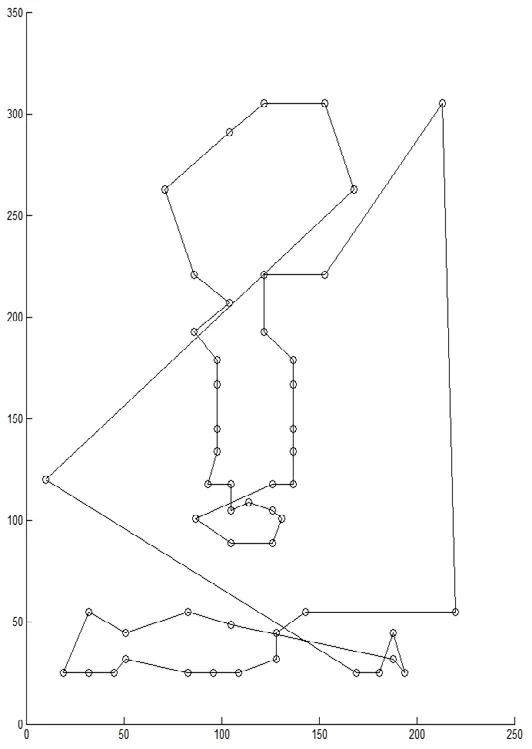
图1 迭代计算10次变电设备巡视最优路径

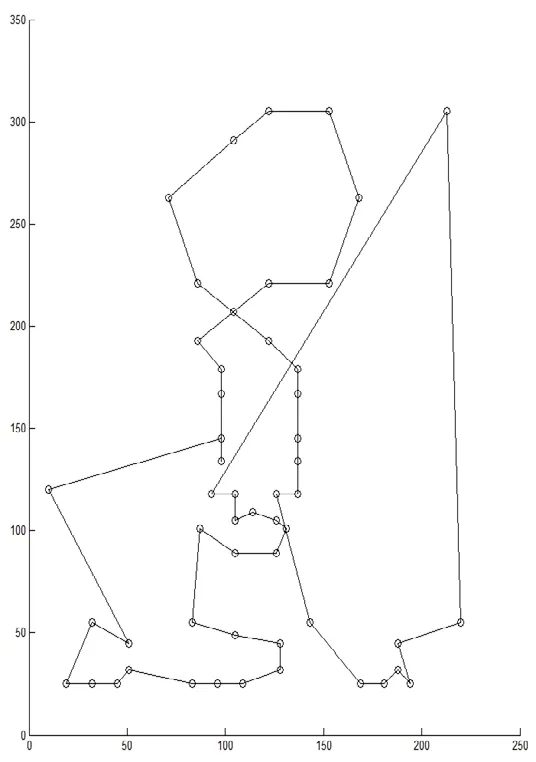
图2 迭代计算50次变电设备巡视最优路径

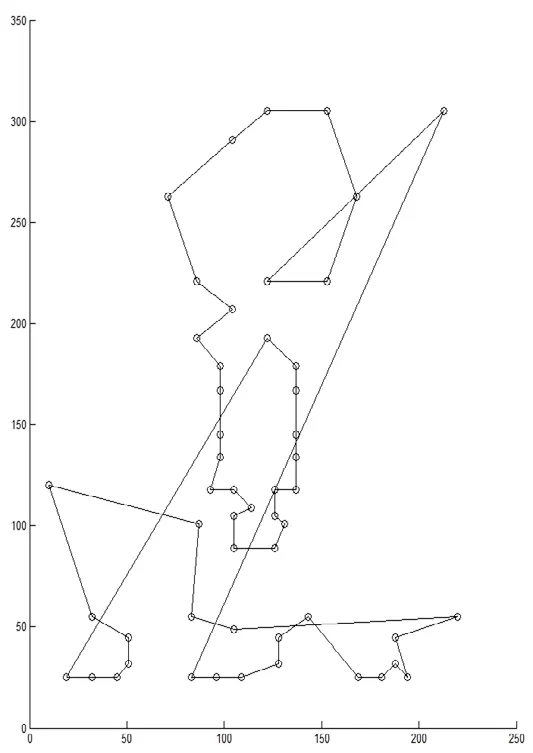
图3 迭代计算100次变电设备巡视最优路径

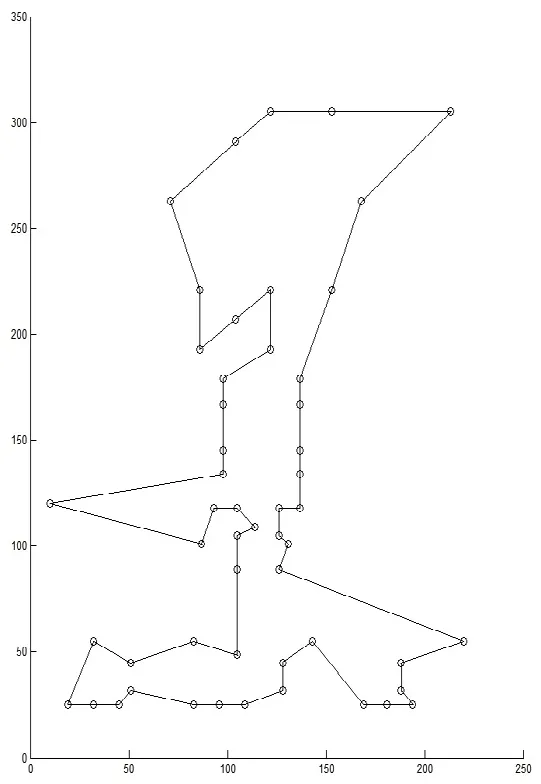
图4 迭代计算200次变电设备巡视最优路径

图1至图4分别展示了各次迭代进化后，所求解的最优路径情况，从路径的形状可见，早期求得的最优路径错综复杂，存在一定的迂回折返现象，致使总路程较长，而经过一定数量的迭代后，算法逐渐寻求到更优解，路径也变得更加简洁，因此总路程也随之变短。

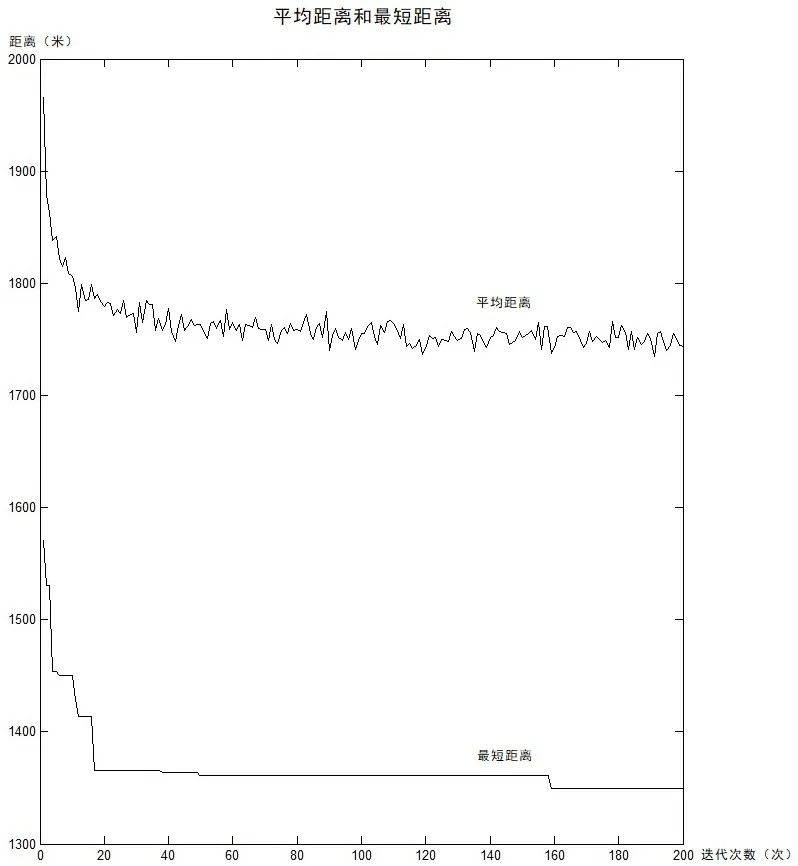
图5 改进粒子群算法求变电站设备巡视路径最优解过程

图5显示了改进粒子群算法求解变电站设备巡视路径问题最优解的演化过程，即迭代次数与最优解之间的关系，说明随着迭代次数的增加，最优解结果也逐渐趋向于最短。

4 结束语

本文采用了一种改进粒子群算法，研究了变电站设备巡视路径优化问题，运用引进进化变异粒子个体，并且对惯性权重进行自适应调整，实现了粒子种群的动态更新。使算法既能够在运算的早期提高算法的探索能力，避免运算停滞，又能在运算的后期找到最优解并迅速收敛，提高求解速度。并通过实例验证了所提出方法的研究性，对于实际电网有一定参考价值。