基于特征模型的疏浚过程中泥浆浓度控制系统设计
朱师伦, 高 岚, 徐合力, 潘成广
(武汉理工大学 a. 船舶动力工程技术交通行业重点实验室; b. 能源与动力工程学院, 武汉 430063)
疏浚是经济建设的基础性工作,涉及经济发展和社会进步的诸多方面,如港口航道建设与维护、临海工业区建设与沿海城市发展、江河湖库防洪清淤、环境保护和海洋资源开发等。[1]绞吸挖泥船作为实施相关疏浚工程的主要设备载体,在实际施工中为使其安全、稳定、高效地运行,操作人员需根据长期的工作经验来操作。疏浚船舶的实际生产量不仅与自身设备的技术参数有关,而且与实际工程的土质和风浪条件等外界因素紧密相关。长期以来,疏浚作业的经验依赖性强,效率低下,利用自动化手段是解决该问题的有效途径。[2]
国外的疏浚作业自动化研究始于20世纪90年代,许多机构都开展了大量的研究工作,但对外公开的关于绞吸挖泥船泥浆浓度控制的研究很少,很难深究其实质和具体性能。国内相关研究工作已开展近10 a,但关于泥浆浓度的研究较少。王庆丰等[3]针对泥浆浓度控制,采用可测干扰的受控自回归滑动平均模型描述泥浆浓度控制模型,基于该模型提出一种参数自校正前馈控制方法来实现泥浆浓度的稳定控制。朱文亮等[4-5]针对泥浆浓度控制,利用BP(Back Propagation)神经网络构建以横移速度为控制输入、以泥浆浓度为输出变量的状态空间模型,研究挖泥船疏浚过程的变化规律,在该模型的基础上引入横移速度和加速度约束,设计二次型泥浆浓度最优控制跟踪器。高国章等[6]针对挖泥船采用的传统的泥浆浓度比例微分积分控制器(Proportion Integral Differential, PID)难以保证产量和效率稳定性的缺点,从工程实用的角度出发,利用模糊控制与PID控制相结合的方案加以优化。这些研究对绞吸挖泥船泥浆浓度控制的发展有极大的推动作用。
绞吸挖泥船泥浆浓度控制的关键问题主要涉及建模困难、不确定性和时滞性等控制难点。一方面,从机理出发建立精确的泥浆浓度过程数学模型极为困难,限制了控制方法的研究;另一方面,疏浚作业系统的复杂性使研究的控制方法复杂化。综上所述,本文从工程应用的角度出发,采用“特征建模”理论,构建泥浆浓度过程模型,基于该模型设计全系数自适应控制器,实现疏浚作业过程中泥浆浓度的自动化控制。[7-8]
1 疏浚作业系统分析
绞吸挖泥船吸扬系统包括土壤切削系统和泥浆输送系统,是施工过程中真正产生效益的过程。绞吸挖泥船吸扬系统结构见图1,其中土壤切削系统是挖泥船的重要组成部分,其在水下切削土壤的过程是土壤、机械和水流相互作用的过程,机理复杂,泥浆的生成主要与这个部分有关。
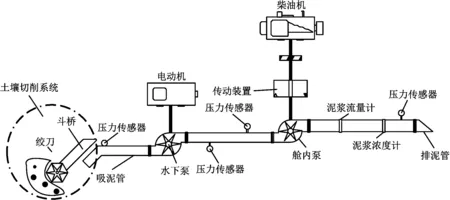
图1 绞吸挖泥船吸扬系统结构
根据前期研究和图1得到实际泥浆形成过程见图2。
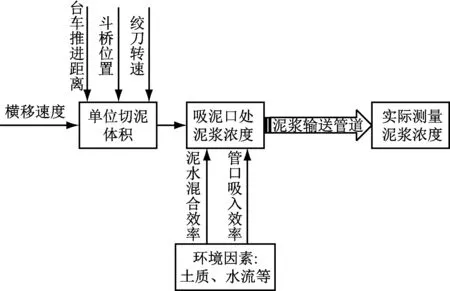
图2 实际泥浆形成过程示意
泥浆浓度过程即挖泥船土壤切削系统搅动河床底部泥沙形成沙水混合物,并在泥泵抽吸作用下进入吸口形成泥浆的过程。泥浆浓度过程动态特性非常复杂(如图2所示),影响泥浆浓度的因素较多,主要包括实际的土壤切削量、泥水混合效率和管口吸入效率等。因此,从工作机理出发建立泥浆浓度过程的数学模型较为困难,且具有一定的局限性。从过程控制的需要出发,利用数据驱动的思想建立泥浆浓度过程模型是解决该问题的一个新思路。
2 泥浆浓度过程特征建模
特征模型是指不依赖精确建模,从控制的角度出发,将研究对象模型重构成反映控制要求和系统主要输入与输出关系的低阶差分方程形式,使同样输入控制作用下的特征模型和实际被控对象的输出在动态过程中能保持在允许的误差范围内。该方法为高阶、参数未知对象的低阶控制器设计提供理论依据,具有工程化实际应用方便的特点。[9]
2.1 泥浆浓度过程特征模型的推导
在挖泥船施工中,主要通过调节单位时间内的土壤切削量来控制泥浆浓度。土壤切削量与台车推进距离(纵向切泥厚度)、斗桥位置(垂直切泥厚度)和横移速度等有关。在施工中,台车推进距离和斗桥位置一般不能连续调节,因此单位时间内的土壤切削量主要通过调节横移速度来实现,据此建立横移速度和泥浆浓度的特征模型。
泥浆浓度过程是一个典型的非线性系统,可表示为
(1)
式(1)中:u为系统输入,即横移速度;y为系统输出,即泥浆浓度。
由于疏浚机理的复杂性,在对泥浆浓度过程进行分析时,需对其进行必要的简化,并确定一些基本假设。简化和假设如下:
1) 控制量u(t)的次方为1。
2)f(·)中的全部变量y(t)、u(t)为0时,则f(·)=0。
3)f(·)对所有自变量连续可导,且各偏导数值有界。
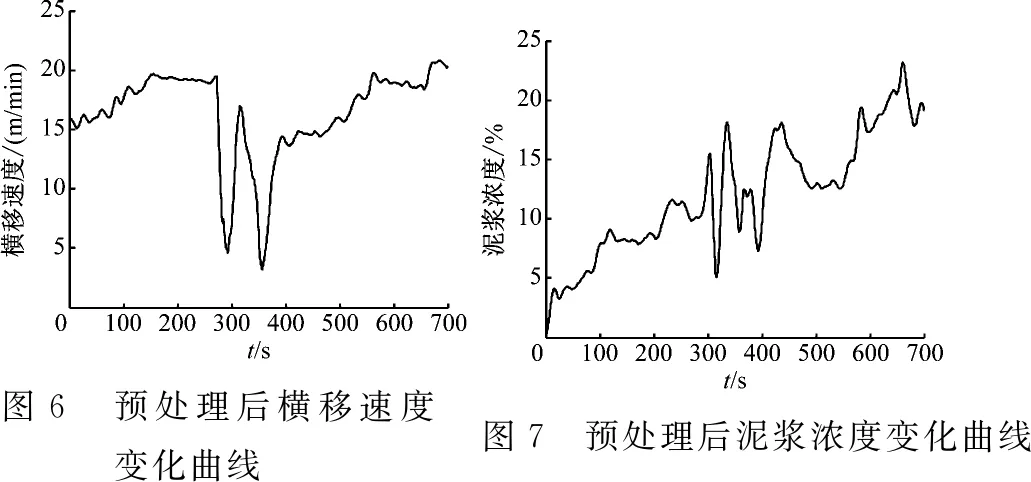
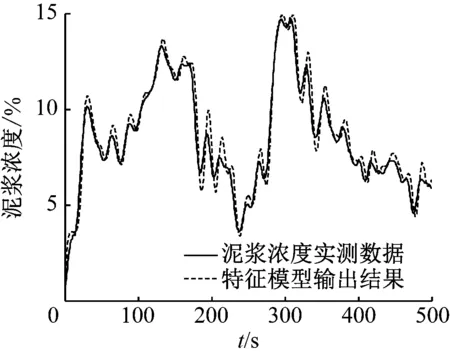
4)|f(y(t+Δt),u(t+Δt))|-|f(y(t),u(t))| 5) 在实际工程中,控制量总是有界的,各自变量y(t)和u(t)也是有界的。 根据假设1)和中值定理对该非线性系统进行推导,有 (2) (3) (4) 对式(2)进行形式变换,有 (5) 为方便表述,记 (6) 对式(5)求微分,有 (7) (8) 将式(5)与式(7)相加,进行近似离散化整理,有 (9) 式(9)中: (10) (11) Δtβ1(k) (12) (13) (14) 将式(9)标准化,写成参数估计方程为 y(k)=f1(k)y(k-1)+f2(k)y(k-2)+ (15) g0(k)u(k-1)+g1(k)u(k-2) 式(15)中: (16) (17) (18) (19) 绞吸挖泥船在施工过程中参数变化频繁,工作周期较长。如果要求极精准控制,既会对控制器有很大负担,又会使执行器长期处于调整状态,对其工作寿命产生很大影响。因此,在不过度追求控制精度的前提下,输入仅取g0(k)。同时,考虑到时滞性问题,将式(15)简化为 y(k)=f1(k)y(k-1)+f2(k)y(k-2)+ g0(k)u(k-k0) (20) 式(20)中:k0为滞后步数;f1(k)、f2(k)和g0(k)为特征参数,在工程应用中作为时变参数处理。 以上推导证明:泥浆浓度过程可重构为特征模型的形式。 特征建模的理论基础之一是“全系数之和等于1”。然而,上述二阶差分方程特征参数之和不一定满足该条件。因此,通过在被控对象前串联一个比例环节C′来构建广义对象,使其满足“全系数之和等于1”的条件。C′为 (21) 广义对象示意见图3。 图3 广义对象示意 广义对象的特征方程为 y(k)=f1(k)y(k-1)+f2(k)y(k-2)+ (22) 综上所述,构造泥浆浓度过程的特征模型的形式如式(22)所示。 根据上述分析可得特征参数是不确定、时变的。采用带遗忘因子的递推最小二乘法对特征参数进行在线辨识。将式(22)特征模型转换为最小二乘格式,有 y(k)=φT(k-1)θ(k) (23) (24) (25) 带有遗忘因子的递推最小二乘估计为 (26) 式(26)中:通过试验整定,初步选取遗忘因数λ=0.97。 2.4.1数据预处理 数据来自于长江航道局某型自航绞吸挖泥船舶在某工地现场实际疏浚施工过程中采集的数据,采样周期为0.5 s。现截取部分数据,得到实测横移速度和泥浆浓度变化曲线见图4和图5,时间为13:05:30—13:15:15。 由图4和图5可知:实测数据中的野点和高频成分会对分析泥浆浓度过程的特性造成干扰。因此,需对数据进行野点剔除和滤波等处理,这是后续工作开展的必要环节。处理后的数据见图6和图7。 图4 实测横移速度变化曲线图5 实测泥浆浓度变化曲线 图6 预处理后横移速度变化曲线图7 预处理后泥浆浓度变化曲线 利用计算机对处理后的数据进行离线辨识,确定系统时滞时间约为10 s,即k0=20。 2.4.2模型验证 从实测数据(包括图4和图5的数据)中截取3部分,用于检验泥浆浓度过程特征模型的可靠性。特征模型的输入为实测横移速度,特征模型的输出值与该横移速度对应的实测浓度数据对比见图8、图9和图10。 图8 特征模型验证曲线1 图9 特征模型验证曲线2 图10 特征模型验证曲线3 由图8、图9和图10可知:特征模型和实际浓度过程的输出曲线基本吻合,除了在起始阶段的较短时间内,由于参数辨识的缘故,参数波动较大,其余阶段特征模型的输出值与泥浆浓度实测值之间的误差值不超过2%,在动态过程中能保持在允许的输出误差范围内,特征模型能很好等价于实际泥浆浓度过程。 浓度控制的目标是将管道泥浆浓度维持在给定的期望浓度水平上。从前面的分析中可确定泥浆浓度控制系统是复杂的带滞后环节的非线性时变系统,针对该系统设计的泥浆浓度控制系统见图11。 采用基于特征模型的全系数自适应控制方案对泥浆浓度进行控制如图11所示。全系数自适应控制理论是针对一类参数未知时变对象的自适应控制方法,已得到大量实际控制工程的考验。[10]根据控制需求,设计的全系数自适应控制器由非线性黄金分割控制器和维持跟踪控制器协同作用。 图11 泥浆浓度控制系统示意 非线性黄金分割控制方法主要是为参数未知对象实现有效控制服务的,与目前已有的各种自适应控制方法相比具有独特的优点,即能保证过渡过程阶段参数未收敛时的闭环系统稳定。尤其是对于绞吸挖泥船这类对象而言,当不允许现场反复调试时,该方法具有很好的控制效果。非线性黄金分割控制既保证控制系统的稳定性,又具有很好的鲁棒性和适应性等控制性能。 非线性黄金分割控制律表示为 (27) (28) (29) (30) (31) 维持跟踪控制量uw(k)主要用来保证系统输出y(k)跟踪期望浓度yr(k)。维持跟踪控制律表示为 (32) 式(32)中:λw为较小的正数,用于增加系统的鲁棒性。 (33) 式(33)中:f为滤波系数,一般取(0.1, 0.5)。 将设计的控制器与工业生产控制中广泛应用的PID控制器相对比。PID控制器的参数按试误法整定,考虑到时滞性的影响,在系统中利用经典的微分先行控制加以改善。仿真中系统的采样周期与实际疏浚过程保持一致,为0.5 s。针对疏浚作业中的两种典型工况进行仿真试验。 根据实船考察,在挖泥船施工中,大多希望泥浆浓度在作业过程中保持稳定,泥浆浓度恒值控制是挖泥船施工中最重要的工作状态。设定期望浓度为20%进行仿真试验。 在实际疏浚作业过程中,吸泥口处由于土壤切削过程不断产生泥浆,只能在排泥口处测量泥浆浓度,存在测量时滞现象(如图2所示)。为更加直观地分析控制器的性能,采用仿真的方式对吸泥口处的泥浆浓度进行分析。 由于外部有随机干扰(土质、水流等),被控对象是不确定、时变的。泥浆浓度恒值控制试验曲线见图12。由图12可知:传统PID控制器在应对这样的对象时不具备良好的控制性能,尽管能将泥浆浓度稳定在期望值附近,但误差较大。相反,全系数自适应控制器在应对这种情况时,控制器参数动态调节,具有很好的适应能力(见图13)。 全系数自适应控制器控制误差曲线如图13所示。由图13可知:全系数自适应控制器响应速度快,在约3 s时就能跟踪到期望值。跟踪到期望泥浆浓度后,在应对疏浚过程中土质、水流等外界随机干扰时,控制系统输出能一直维持在期望浓度附近,浓度误差率能控制在5%以内,具有很好的浓度保持性能。 a) PID控制器 b) 全系数自适应控制器 图13 全系数自适应控制器控制误差曲线 在绞吸挖泥船施工过程中,当外界因素发生较大改变时,为保证疏浚生产效率,期望泥浆浓度需随之调整。因此,泥浆浓度跟踪同样是疏浚作业中必不可少的工况。设计仿真试验,分别在t=50 s、t=100 s、t=150 s时,使期望泥浆浓度由20%突变到30%、25%、15%(见图14和图15)。 a) PID控制器 b) 全系数自适应控制器 图15 全系数自适应控制器控制误差曲线 由图14和图15可知:在泥浆浓度跟踪试验中,全系数自适应控制器的性能更好,其响应速度快,具有很好的跟踪性能,控制性能稳定,在不同期望泥浆浓度设定值的下,泥浆浓度误差基本上没有变化,不存在控制目标不同、控制性能不一致的情况。上述试验结果充分证明全系数自适应泥浆浓度控制器具有稳定性好、响应速度快和跟踪效果好等特点。 为提高绞吸挖泥船的生产效率,采用自动化手段代替人工操作,实现疏浚作业过程中对泥浆浓度的控制。针对泥浆浓度控制系统存在的建模困难、不确定性及时滞等控制难点,设计了基于特征模型的泥浆浓度全系数自适应控制器。仿真试验结果表明:该控制器不仅具有稳定性好、响应速度快和跟踪效果好等优点,而且设计简单,具有很强的工程实用性。
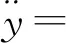
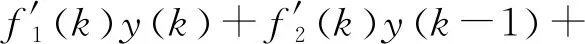
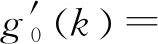
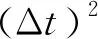
2.2 构建广义对象

2.3 特征参数辨识
2.4 特征模型的验证



3 泥浆浓度的全系数自适应控制器设计
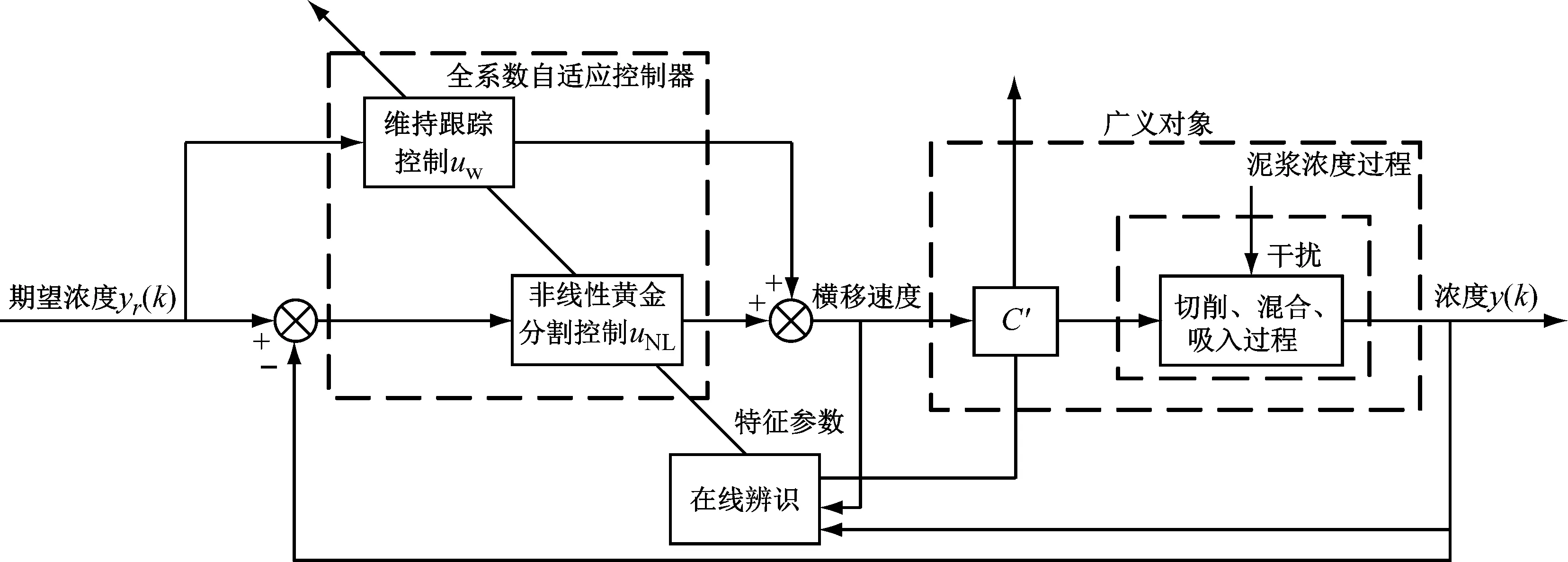
3.1 非线性黄金分割控制
3.2 维持跟踪控制
4 泥浆浓度控制系统仿真
4.1 泥浆浓度恒值控制
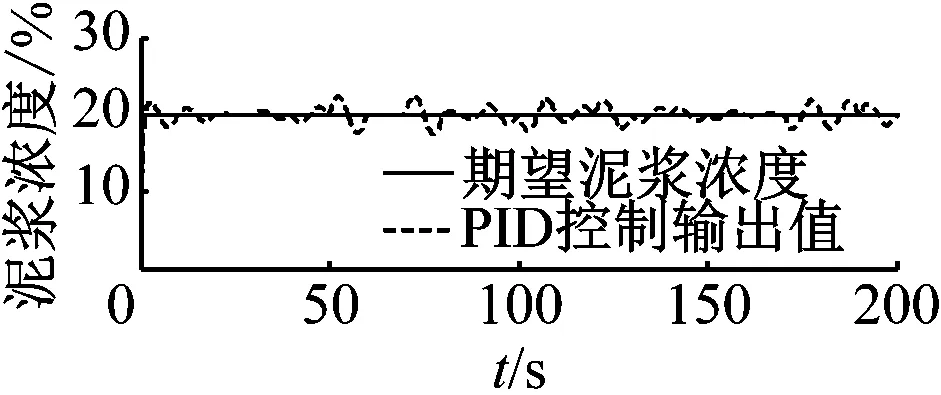
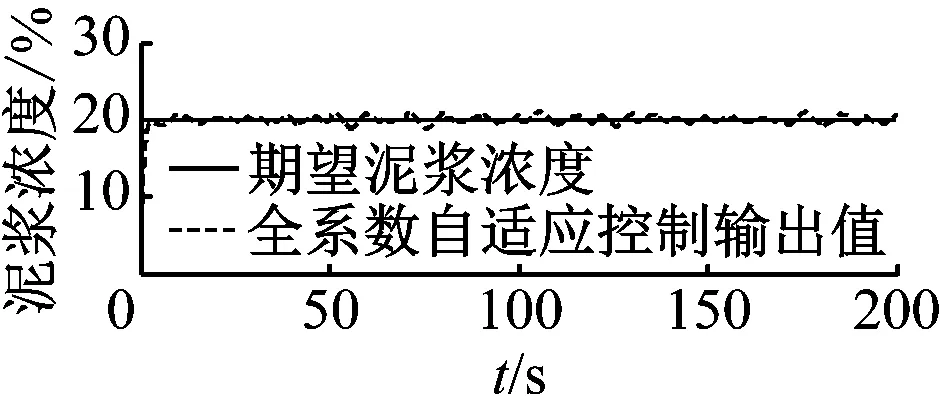

4.2 泥浆浓度跟踪控制

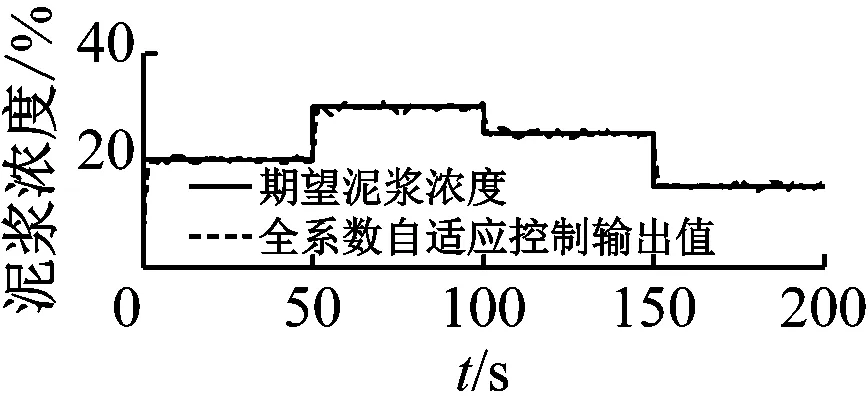

5 结束语

