基于核函数的企业经济决策方案评价研究

游星

（成都理工大学管理科学学院，四川 成都 610059）

经济效益和发展速度之间的关系问题是急需要解决的重要问题。其中效益相关的问题更加重要，不仅需要让经济发展速度得到加快，还需要对经济发展形式进行转变，促进企业经济效益的提升。通过综合评价和分析制约企业发展的因素，帮助找出合适的解决方法和手段，实现资源的优化配置。还能够帮助企业制定与自身实际情况更符合的发展战略，提升企业的素质水平，促进经营管理的完善，对市场动向及时掌握。帮助企业内部和外部矛盾的有效解决，让企业的潜力得到最大的挖掘。

一、核主成分分析法基本内容

核主成分分析法，就是把多个不同的变量综合起来，让其成为少数变量的多元统计学方法，能够对变量之间的线性关系进行更有效的处理。本次研究当中选择了核主成分分析法，把原变量空间借助于非线性变化映射到更高维度的空间。通过核技巧，只需要在源空间当中完成点积运算，不需要知道φ的具体形式是什么。应该选择合适的核函数，让其变成第一成分贡献率达到标准，这样可以有效解决上述遇到的问题。

主成分分析模型，也就是PCA分析模型，假设样本数据向量用，需要将原始变量给标准化。然后可以得到样本协方差真，相关系数阵采用：

在主成分分分析的过程当中，通常情况下是要求主成分的贡献率超过85%。然后将其推广到非线性的情况下中。

核主成分分析法也就是KPCA模型，所依据的原理是：

第一，要把源空间数据，借助于非线性变化将x-X投影到特征空间F当中，假设特征空间，用：表示，可以满足。在非?然的所有特征值 )0( ≥λλ与特征向量V满足下列标准；所有解都在子空间当中。

第二，选取合适的核函数。在核主成分分析法的应用过程中，选取合适的核函数，不需要对变换Φ的具体形式有全面的了解。最后让其转化成为Kij= Φxi⋅Φ ，，可可以以选选择择具有差异化的核函数，最终所得到的结果也是不同的。因此，核函数的实际选择过程是十分关键的，比较常见的核函数类型主要有神经网络核函数，高斯核函数、多项式核函数。

第三，核函数评价具体步骤如下：1.将样本x初始化输入，最终得到矩阵l；2.然后可以求到矩阵K1；3.求取矩阵k1/l的特征值以及特征向量；4.找到最大特征量以及特征向量；5.需要对每个评价样本的系数进行计算，完成综合评价。

二、分析企业经济效益的主要传统方法

（一）因素分析方法

企业生产活动开展当中，会受到很多因素的影响。各种不同的因素最终对企业产生综合性影响，就成为综合性影响因素。当然这些因素并非固定不变的，会受到外部因素影响。对综合性经济影响因素进行分解，可以找到影响综合性指标完成的具体因素是什么，对责任进行划分。此种方法将其称之为主要因素，分为差额计算和连环替代方法。

（二）平衡分析方法

主要是对存在着平衡关系的各种经济因素依存性开展相应的分析，对实际情况和计划情况的差异开展对比分析，了解经济指标发生变动各种因素的影响情况。借助于此种方法开展分析，可以了解到企业在生产经营活动当中出现的不平衡情况，然后再制定相关的措施，确保企业可以更加稳定和持续发展。平衡分析方法还可以继续划分为不同的方法，如增长速度、全额以及余额平均法。

（三）比较分析法

主要是对指标进行对比分析，从数量的角度来确定相关的差异。此种方法的主要作用在于可以对工作的差距和成绩进行有力的说明，采取更加有效的对策，挖掘多重潜力，属于应用范围比较广泛的方法。

三、以核主成分分析法评价企业的经济效益和决策方案

（一）企业的基本情况

盈利指标是对企业经济效益以及决策方案开展评价的重要评价指标。按照会计要素内部的各种联系，可以发现利润总额、产品销售收入、总产值以及总体销售率等都是评价企业经济效益和决策水平的重要指标。但是在综合分析当中，这些指标并没有得到什么明显的体现，从这方面考虑，对比分析和主成分分析和主成分分析方法，选择了2018年某地区的5家企业（表1），处理相关经济效益评价指标，分析这些指标的主要成分，对企业整体经济效益情况开展评价，也给管理层做出更加合理科学的决策提供正确的建议。

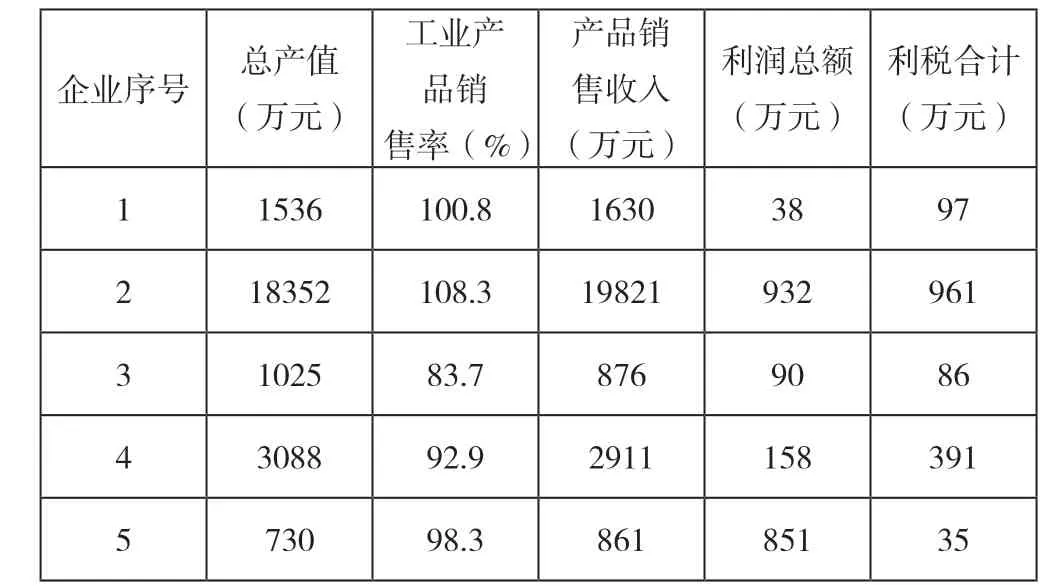
表1 5家企业主要经济效益评价指标

（二）主成分方法评价企业的经济效益

表2为采用主成分分析方法评价企业经济效益的过程。

表2 主成分法评价企业经济效益结果

1.将经济效益的指标进行同趋势化处理，对于可能存在的负值直接转化成正向指标。

2.借助于专门的数据处理软件，如Matlab6.5，标准化处理纳入的研究数据。

3.之后需要计算矩阵的特征值和特征向量，然后完成特征值累积和方差贡献率，如表3所示：

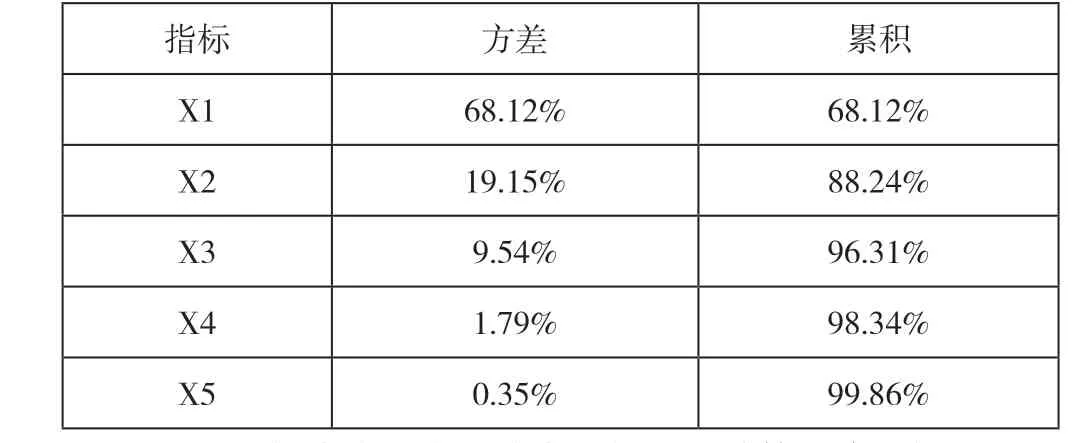
表3 经济指标的特征和累积方差贡献率

4.对指标当中的主成分完成提取，计算经济指标的评价系数。累积的贡献率达到了88.24%，完成前两个主成分的提取。得到最终的评价系数，所得到的评价函数为：

根据以上采用主成分分析方法对企业的整体经济情况进行分析，我们能够发现对于企业经济发展累积贡献率最大的是X1，代表的是总产值。然后分别是工业产值，要让累积的贡献率超过85%，选择了前两个不同的主要成分，也就是工业产品销售率以及工业总值等，其中占据主导地位的是工业总值。这就提醒想要让企业的经济效益得到提升，提升企业的工业总产值，结合市场需求变化，改革与创新现有的技术，让企业的整体素质水平得到提升，让其可以在当前如此激烈的竞争当中获得一定的优势，让工业产品的销售率得到提高，也让企业的经济效益得到提升。

（三）核主成分分析法对于企业的评价作用分析

所采取的评价步骤具体为：

1.标准化处理纳入本次研究的5个企业的相关数据。因为上述分析方法当中有提及和分析，此处不再详细描述。

2.核函数的选择需要结合实际情况，通过多次试值与对比引入的数据，确定本次使用的是多项式核函数。确定S=0.05，d=3，C=0，一起来得到矩阵k。

3.然后需要求得矩阵k的特征值和特征向量。找到最大特征值，也就是 maxλ=1.127时情况下最大的特征向量。得到的结果为：

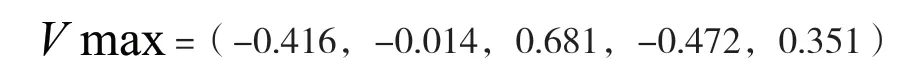
4.计算各个影响因素的主要贡献率，提取核函数当中的主要成分，构建起评价函数。所构建起的评价函数为：F=0.0921F1。表4为核主要成分分析法对企业主要经济情况评价的特征值以及贡献率统计结果，如下表所示：

表4 核主成分分析法特征值和贡献率统计结果

根据表4通过核主成分分析法评价企业的实际经营情况之后，发现X1也就是总产值的贡献率是最大的，这就说明了企业经营当中工业总产值所占据的地位是主要地位。在5家企业当中，第2家企业的工业总产值是排在第一位的，有着比较明显的降维效果。

（四）核主成分分析法的优点分析

与传统的主成分分析法相比，此种核函数的分析方法当中一般会涉及很多的指标。第一次拟合过程本质上为特征空间当中正交变换环节的开展，第二次属于特征空间中对样本数据的投影，完成主成分的相关计算。另外此种方法可以对那些非线性数据开展计算，让指标之间一些隐藏不容易被发现的内在联系得到充分地显示，主成分的贡献率效果是更加明显的。另外实际对比结果显示，在第一主成分的分析过程中，核主成分分析法的累积贡献率是可以超过90%的，与主成分分析方法相比，准确性更加显著。

四、结束语

本次研究中通过引入核函数对企业的实际经营情况进行评价，还发现了核函数与常规主成分分析法之间的差别，帮助企业领导制定更科学的决策，为企业良好发展奠定基础。