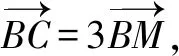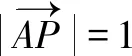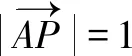例谈变换在高中数学的应用
杨伟达 杨家隽
(1.广东省广州市花都区第二中学 510800;2.广东省广州市花都区实验中学 510800)
在解题教学中,转化与化归不仅是一种重要的解题思想,也是一种最基本的思维策略,更是一种有效的数学思维方式.其中变换是转化和化归的一种形式,在解题中常常用到.如变换位置、变换数值、变换视角等,它往往会激起学生的思维之花,开启数学思维之门,在解题中起到四两拨千斤的效果.
一、变换位置
有这样的一类几何题,直接用传统方法求解、证明往往比较困难,此时需要转化思路,寻找等价条件,变换一个位置,此时问题就会迎刃而解.变换位置常常有变换点、变换线、变换角等.
1.换点
在等价条件下,用某个点替换另一点达到快速解题.这一方法常常成了解决立体几何中线面距离的常规手法.
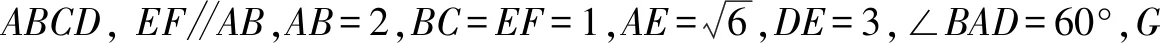
分析利用传统方法作垂线求点F到平面BED的距离比较困难,不妨利用线面平行的性质,转移到另一点位置,从而转化为求另一个点到面的距离(方便求得).再利用等体积法间接求高.

解(1)略.(2)略.
(3)如图2,由(1)FG∥平面BED.
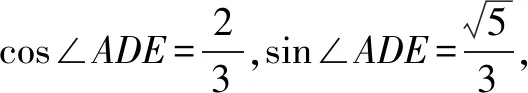
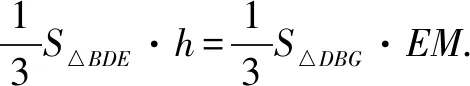


2.换线
有这样的一类题,在涉及线段长度之和时,用某一线段替换一线段,以直代曲,从而达到方便解题.比如几段线段之和求最值问题等,在几何中时常碰到的题型.

分析本题考查了立体几何两动点问题,在涉及两段或两段以上的线段之和,通常采用以直代曲即可解决.本题最根本的办法是转化为同一平面,找对称、找全等,目的是替换某线段长度,最终达到两点间线段最短.




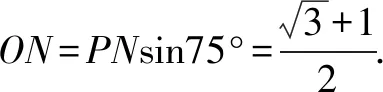
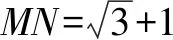
3.换角
有这样的一类题,在等价的条件下,通过平移(或者替换)一条线段或两条线段,达到角度的变换,进而可将问题解决.比如,空间角转化为平面角、弦切角、圆周角等等.
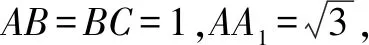
分析在涉及求异面直线的夹角时,常常平移直线到某一点.解题的策略是异面问题转化为平面问题,找到平面上的点,进而找到异面直线的夹角.

解如图4,补上如图所示的相同长方体CDEF-C1D1E1F1,连接DE1,B1E1.
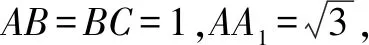

故选C.
二、变换数值
有这样的一类题,直接解题比较困难,发现某一结构类似,比对结构,缺什么补什么,发现某值可以用另一种形式替换,变换数值后,结构齐整,用熟悉的方法即可将问题解决.

分析可将1替换成sin2α+cos2α,采用弦化切,原式可化为含有正切的函数式,代入,计算,求值.

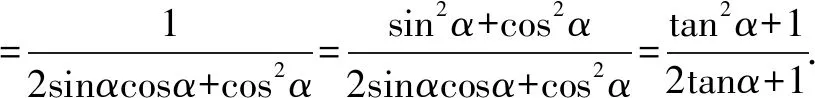
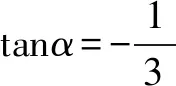
三、变换视角
有这样的一类题,可以从多角度思考,变换视角后,发现这一式子可以用另一个视角去审题,去思考,此时解题常常会豁然开朗.比如数形转换、主元转换、函数与方程转换等等,这种方法另辟蹊径,简单明了,对解题起到事半功倍的效果.