桃芳李艳风景异 融合探究寻本源——2019年北京高考文理科解析几何解答题寻根之旅

江西省南昌三中 (330029) 张金生

神奇的圆锥曲线是连接代数与几何之间的一座桥梁，虽然奥妙，但其实也是有较强的规律可循.随着一线教师对解析几何圆锥曲线内在性质的深入探究，解析几何试题基因图谱逐渐被破译，不仅使教师清晰地理解命题人的思想、命题背景和考查目的，把握高考命题规律，还可以更好地培养学生思维品质，提高学生提出问题、分析问题和解决问题的能力,提高学生的数学核心素养.本文从2019年北京高考文理科解析几何解答题入手，对这对姊妹题进行“融合”分析、探究溯源,进行试题基因揭秘探索之旅.

一、试题呈现与答案

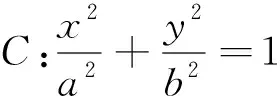
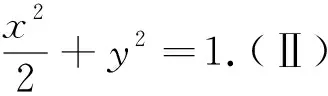
例2 (2019年高考北京卷理科18题)已知抛物线C:x2=-2py经过点(2,-1).

(Ⅰ)求抛物线C及其准线方程;

(Ⅱ)设O为原点,过抛物线C的焦点作斜率不为0的直线l交抛物线C于两点M,N，直线y=-1分别交直线OM,ON于点A和点B．求证:以AB为直径的圆经过y轴上的两个定点.

答案：(Ⅰ)抛物线C的方程为x2=-4y，准线方程为y=1.(Ⅱ)以AB为直径的圆经过y轴上的定点(0,1)和(0,-3).

二、文理两题内在共性

对上述两例进行“融合”探究，可发现它们有内在共性.例1的第二问可改为：(Ⅱ)设O为原点，直线l:y=kx+t(t≠±1)与椭圆C有两个不同交点P,Q，直线AP与x轴交于点M，直线AQ与x轴交于点N，求证：以MN为直径的圆经过y轴上的两个定点.例2的第二问可改为：(Ⅱ)设O为原点，过抛物线C的焦点F作斜率不为0的直线l交抛物线C于两点M,N，直线y=-1分别交直线OM,ON于点A和点B．求证：|FA|·|FB|为定值.这一共性背景是圆内相交弦定理.

三、试题拓展

由例1得以下结论:

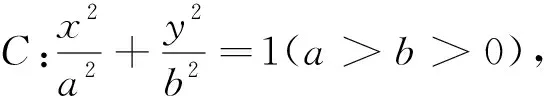
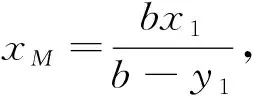
由例2可得以下结论:

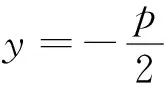
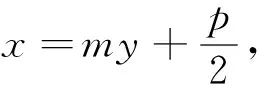
|FA|·|FB|=|FG1|·|FG2|=p2.

四、题根基因探索

揭开试题神秘的“面纱”,抓住考题和题根之间的内在联系.试题生长点是基于圆锥曲线的通性性质，是许多高考试题的题源题根.

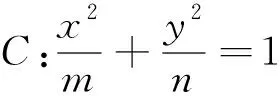
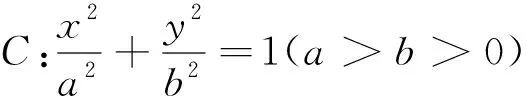
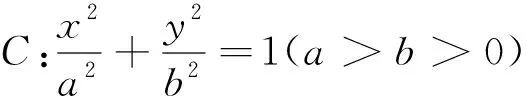
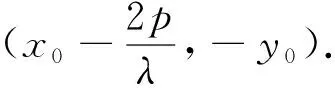
水有源，故其流不穷；木有根，故其生不穷.很多考题本质是题根穿上华丽的“外衣”，带上神秘的“面纱”，抓住考题和题根之间的内在联系，解题时才能“莫为浮云遮望眼”，善于“拨开迷雾”见“真颜”，才能从茫茫题海中走出来，可谓茫茫题海，寻根是岸.教学中，我们应将具有探究价值的题根挖掘出来,也可进行问题情境的设置，让学生在探究中内化新知并建构完善知识体系，充分体会题根的价值，并获得思维能力和核心素养的长效发展.