波流作用下围网养殖工程的桩柱结构受力分析

桂福坤，张斌斌，曲晓玉，王 萍，邵振宇，冯德军※

（1. 浙江海洋大学国家海洋设施养殖工程技术研究中心，舟山 316022；2. 浙江海洋大学水产学院，舟山 316022）

0 引 言

桩柱式围网是一种新兴的养殖模式，具有养殖水体大，鱼类活动空间广，养殖环境更贴近自然，养殖对象品质更接近野生等优点。近年来中国围网养殖发展迅速，目前已在浙江、福建、山东等地建成多处大型围网养殖设施。浮绳式[1]和桩柱式[2]（离岸双圆周桩柱式、联岸双排桩柱式）是大型围网养殖工程的主要结构形式。相比较而言，桩柱式围网养殖工程由于安全系数高而更受养殖企业青睐。然而，与其他海上养殖设施一样，波浪和潮流是其面临的最大挑战，强波流作用会使桩柱结构遭到破坏，造成鱼群逃逸，给养殖企业带来严重的经济损失[3]。因此，研究波流作用下桩柱式围网养殖设施的结构稳定性对围网工程结构设计、建造施工和日常管理维护等都具有重要的实际工程意义。

桩柱式围网设施主要由桩柱系统和网衣系统两部分组成。针对围网网衣系统，陈天华等[4-7]通过物理模型试验和基于集中质量的数值模拟方法系统地研究了波浪和水流作用下网衣的水动力特性，为围网网衣系统的设计和装配提供了指导。然而，专门针对围网桩柱系统的相关研究鲜有报道，已有的研究大多针对跨海大桥、海洋平台基础等典型海洋工程结构。Liu 等[8]通过物理模型试验研究了波流联合作用下东海大桥倾斜群桩基础的受力与波流参数的关系。Deb 等[9]利用ABAQUS 软件模拟了桩筏基础在水平和竖直联合动力荷载作用下的动力响应，研究结果表明竖直动力荷载对桩柱侧向响应有重要影响，在结构设计时不可忽视。黄茂松等[10-12]系统地研究了土反力-位移关系（p-y 曲线）的构造方法，提出了基于弹性迭代计算获得塑性变形场和边界荷载的弹性虚拟加载上限的方法，并应用该方法研究了二维水平受荷桩的动力响应问题，讨论了刚度比和土体应力-应变曲线形式对桩身响应的影响。通过假定地基反力系数沿着水深呈线性增加，赵明华等[13-17]得到了桩身响应的解析解，给出不同力学参数对桩柱变形的影响。黄晓亮等[18]通过对组合桩的水平承载力载荷试验和计算分析，得到组合桩地基土水平抗力系数比例系数值和组合桩的抗弯刚度的计算方法。上述研究虽然不是直接针对围网桩柱结构，但是相关的研究方法和研究结果可为围网桩柱系统研究提供有益的借鉴。

综上，现阶段关于围网养殖设施的研究主要为围网网片系统水动力特性研究，对于桩柱结构力学特性的研究基本处于空白。为此，本研究采用Winkler 地基梁理论[19]，结合线弹性地基反力法中的常数法[20]，系统研究波流作用下桩柱的动力响应特点，分析水平位移和弯矩沿水深方向的变化规律，明确最大位移和最大弯矩与水流速度、波高之间的关系，确定桩柱结构变形后的危险截面以及遭到破坏时的临界动力条件，以期为桩柱式围网结构的设计和施工提供依据。

1 研究方法

1.1 围网桩柱模型

桩柱式围网养殖结构由网衣系统和桩柱系统组成（图1），水流和波浪沿y 轴方向传播。根据陈天华等[5]研究，采用集中质量点法计算网衣系统在水流、波浪作用下的受力，在目脚上建立局部坐标系（ξ,η,τ），τ 方向为沿目脚方向，ξ 轴在τ 和水质点相对速度VR组成的平面内与τ 垂直，η 与τ 和组成的平面相垂直。在整体坐标系下将各集中质量点所包含的结节和目脚的受力进行累加，并将其分配到集中质量点上，然后利用牛顿第二定律建立质点运动方程如式（1）所示。

式中ΔM、M 分别表示各集中质量点的附加质量和质量，kg；a 表示各集中质量点的加速度矢量，m/s2；T 表示集中质量点所受到的张力矢量，N；FD、FI分别表示集中质量点的速度力矢量和惯性力矢量，N；W 表示质点的重力矢量，N；B 表示质点的浮力矢量，N；CD表示速度力项系数；A 表示网线沿波浪方向的投影面积，m2；CM表示惯性力项系数；Cm表示附加的质量力项系数；d 为网线直径，m；l0为网线原始长度，m；l 为变形后的长度，m；C1、C2为构件材料弹性系数[5]，其中C1=345.37×106，C2=1.012；wρ 为海水密度，kg/m3；ε 为网线伸长率；v 为水质点速度，m/s；t 为时间，s。

图1 桩柱式围网养殖结构示意图 Fig.1 Schematic diagram of pile-type net enclosure aquaculture facility

本研究主要关注yoz 平面（图2）内的桩柱结构在水流、波浪、水深和埋深作用下的力学特性。模型以海床面为界分为上、下2 部分，海床面以上结构受到波浪和水流作用，海床面以下部分土体分层离散为若干个相互独立的弹簧，桩底采用铰接方式与海床连接。作用于海床面以上桩柱结构的波浪力和水流力，采用如下式（2）计算：

式中Cw为水阻力系数，取值1.4[21]，A1为桩柱和网衣迎流面积，m2；Fw为海床面以上桩柱结构受到的波浪力和水流力，MN。

图2 桩柱受力分析 Fig.2 Force analysis of pile

根据张磊等[15,22]的研究，忽略纵向荷载影响，结合欧拉·伯努利梁理论[23]，水平力作用下桩柱结构的力学平衡条件得到桩柱挠曲方程为

式（3）为海床面以上部分桩柱挠曲方程，y′为海床面之上桩柱水平位移，m；z′为海床面之上高度，m；式（4）为海床面以下桩柱挠曲方程，y 为海床面之下水平位移，m；规定向右为正，向左为负，b0为桩柱计算宽度，m；EI 为桩柱抗弯刚度[24]，k 为单位体积土抗力系数[25]，根据海床土力学试验数据求得的平均值，MN/m3；各参数具体计算公式为：

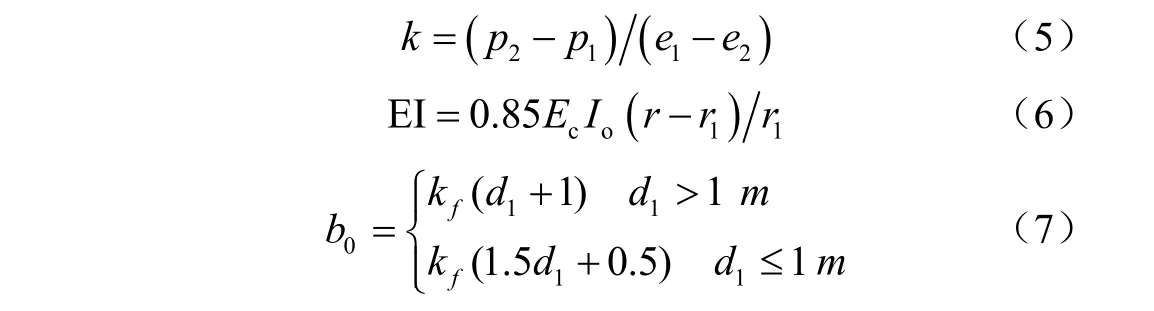
其中kf为桩柱形状系数，圆形桩柱取0.9，方形桩柱取1.0；Ec为混凝土弹性模量[26]；Io为桩身换算截面惯性矩[27]；d1为桩柱直径，m；p1为初始土体压力，MN；e1为土样孔隙率；p2为加载压力值，MN；e2为加载后土样孔隙率；r 为管桩外半径，m；r1为管桩内半径，m。

1.2 计算工况

本文以舟山桃花岛围网养殖工程结构作为研究对象，各参数如下。1）网衣参数：网衣为有结节 PE（Polyethylene）网衣，目脚长度8.32 cm，网线直径3 mm，网目个数57 438，水平缩结系数0.66，垂直缩结系数0.75，网片宽度6 m，高14 m，其中网衣在水下和水上部分分别为12 和2 m；2）纲绳参数：尼龙材质，直径18 mm，沿深度方向每间隔1 m 设置1 根纲绳，两端分别与桩柱连接，网衣受力通过纲绳传递给桩柱；3）桩柱参数：PHC桩，桩柱长度32 m，桩柱直径0.6 m，壁厚0.1 m，桩柱埋深17 m，横向桩间距（y 方向）5 m，纵向间距（x 方向）8 m；混凝土强度为C80，弹性模量Ec=3.8×104MPa，预应力筋为13φ9.0，强度等级HPB400，泊松比0.2，极限弯矩0.246 MN·m；4）动力参数：计算水深12 m，平均潮差4 m，桩长分为入泥深度（埋深）、水深、半潮差和安全超高（1 m）4 部分，水流假设为均匀稳定流，流速取0.8、1.0、1.2、1.5 m/s，在固定波陡（波高与波长之比）为1/10 条件下波高取3、4、5、6 m，波浪和水流方向与结构物垂直。由公式（6）计算得桩柱抗弯刚度为85，由公式（7）可知桩柱计算宽度为1.26 m，根据实际海域现场土力学试验参数和公式（5）计算出该海域内海床土体单位体积抗力系数k=0.411 MN/m3，桩柱结构计算工况如表1 所示。

表1 桩柱结构受力计算工况 Table 1 Force analysis cases of of piles

2 结果与分析

2.1 水流对桩柱结构力学特性的影响

图3 为不同水流条件下桩柱位移和弯矩随标高的变化情况。图3a 表明：相同流速条件下，桩柱结构位移从顶端到底面逐渐减小；不同流速条件下，桩柱结构位移的变化在海床面上部十分显著且随着流速的增加而增大，在海床面下部由于海床土反力作用而发生负向位移且变化不明显，当水流速度为0.8 m/s 时，桩柱结构最大位移0.05 m，当水流速度增加87.5%为1.5 m/s 时，桩柱结构同一深度处的位移明显增大，桩柱结构最大位移为0.18 m，增大2.6 倍。图3b 表明：第一弯矩零点将整个桩柱结构的弯矩变化分为正、负（上、下）2 部分，相同流速条件下，正、负弯矩沿深度方向先增大后减小，当水流速度由0.8 m/s 增加至1.5 m/s 时，桩柱结构同一深度处的弯矩逐渐增大，最大弯矩由0.033 MN·m 增加至0.114 MN·m，增大2.5 倍；由于桩底在计算过程中采用铰接方式处理，弯矩值为0，最大弯矩值点在海床面以下2 m 范围内。针对本文直径0.6 m、极限弯矩0.246 MN·m的 PHC 桩，计算流速条件下，最大弯矩计算值为0.114 MN·m，安全系数为2.158（极限弯矩与最大弯矩之比），说明该结构稳定性好，安全可靠。

图3 不同流速条件下桩柱的力学特性（工况1～4） Fig.3 Mechanical properties of piles under different current velocities (cases 1-4)

2.2 波高对桩柱结构力学特性的影响

图4 为不同波浪条件下桩柱结构位移和弯矩随结构标高的变化情况。由图4a 可知，不同波高条件下，在海床面以上5～15 m 范围内，桩柱结构同一深度处位移变化十分显著。相同波高条件下，位移曲线沿水深方向逐渐减小，最大位移在桩柱顶面，当波高为3 m 时，桩柱结构最大位移为0.133 m，当波高为6 m 时，桩柱结构最大位移增加至0.533 m，增大近3 倍。由图4b 可知：第一弯矩零点将桩柱结构弯矩分为正、负（上、下）2 部分，相同波高条件下，正、负弯矩均先增大后减小；桩柱结构上同一深度处弯矩值随波高的增加而增大。最大弯矩点在海床面以下2 m 范围内；在不同波高条件下，波高为3 m 时，桩柱最大弯矩为0.082 MN·m，当波高为5 m时，桩柱结构的最大弯矩值为0.245 MN·m。本文所研究的直径0.6 m、极限弯矩0.246 MN·m 的PHC 桩结构的安全系数为1.004，此时最大弯矩值接近于极限弯矩，因此，5 m 波高可作为波浪条件下该养殖结构发生破坏的临界条件。

图4 不同波高条件下桩柱的力学特性（工况5～8） Fig.4 Mechanical properties of piles under different wave heights(cases 5-8)

2.3 波流联合作用对桩柱结构力学特性的影响

通过计算对比单纯流速、波高条件下桩柱结构的力学特性发现，当波高大于5 m 时，桩柱结构发生断裂，其余各组条件下结构稳定性较好。然而，在实际养殖海域中，桩柱结构受力较为复杂，往往是水流和波浪联合作用。因此，固定流速为1.0 m/s，通过变化波高来分析波流联合作用对桩柱结构的力学特性的影响。波流联合作用下桩柱的动力响应特性如图5 所示。

图5 波流联合作用下桩柱的力学特性（工况19～22） Fig.5 Mechanical properties of piles under conditions of combined action of wave and currents (cases 19-22)

由图5 可以看出，当流速不变时，桩柱结构同一深度处的位移和弯矩值均随波高的增大而增加。如图5a所示，在第一位移零点（-5 m）以上，桩柱结构同一深度处位移随波高增加而明显增大，而在第一位移零点（-5 m）以下，桩柱结构位移受波高影响较小。由图5b 可知，当水流为1 m/s、波高为3 m 时，桩柱结构最大弯矩值为0.267 MN·m，该养殖结构安全系数为0.921，即桩柱最大弯矩大于极限弯矩，此时，在海床面以下2 m 范围内桩柱截面极易发生断裂，导致整体养殖结构失稳破坏。根据以上分析可知，在水平荷载作用下桩柱同一深度处的位移与弯矩变化规律与前人研究结果相似[28-29]，桩柱位移沿着水深方向逐渐减小，弯矩值先增大后减小；桩身同一点的位移和弯矩随着波高的增加而增大。本文不考虑轴向荷载对桩柱结构变形的影响[30]，在波浪条件基础上增加1.0 m/s 流速，桩柱结构同一深度处的位移和弯矩变化均十分显著。

2.4 埋深对桩柱结构力学特性的影响

波高为5 m 工况下，不同埋深下桩柱结构的动力响应如图6 所示。由图6a 可知，桩柱结构同一深度处位移随埋深的增加而减小，结构稳定性增强，整体结构的最大位移在桩柱顶面，当埋深为10 m 时，桩柱结构最大位移为0.501 m。当埋深为17 m 时，桩柱结构最大位移逐渐递减且变化较为显著，最大位移值减小0.099 m，减小20%。当埋深大于17 m 时，桩柱结构位移变化很小。如图6b 所示，随着埋深增加，桩柱顶端弯矩值逐渐增大，海床面以下2 m 范围内桩柱最大弯矩值逐渐减小，桩柱最大弯矩点的位置随埋深的增大逐渐加深。当埋深为17 m 时，桩柱最大弯矩为0.245 MN·m，接近极限弯矩0.246 MN·m，此时该养殖结构安全系数为1.004。因此，在综合考虑结构稳定性（桩底位移）和安全性的前提下，经济埋深（最小埋深）不小于17 m。

图6 不同埋深条件下桩柱的力学特性（工况9～13） Fig.6 Mechanical properties of piles under different embedded depths (cases 9-13)

2.5 水深对桩柱结构力学特性的影响

图7 显示了波高为5 m 时，水深对桩柱结构力学特性的影响。由图7a 可知，不同水深条件下，海床面上部结构同一深度处位移变化较大且随水深的增加而增大，海床面下部结构同一深度处位移变化很小。当水深为8 m时，桩柱结构最大位移为0.233 m，当水深增大一倍为16 m 时，桩柱结构最大位移随之增大，最大位移为0.625 m，增加近1.7 倍。由图7b 可以看出，不同水深条件下，海床面上部结构同一深度处弯矩变化较为显著且随水深的增加而增大，桩柱最大弯矩在海床面以下2 m范围，随着水深增加，桩柱最大弯矩值随之增大且最大弯矩值点的位置向上移动。当水深为12 m 时，桩柱最大弯矩为0.245 MN·m，接近极限弯矩0.246 MN·m，因此，该养殖结构的安全水深不得大于12 m。综上，建议设计时海床面桩柱露出高度（水深12 m+网衣出水高度2 m+安全距离1 m）与海床埋深比不大于0.8 为宜。

图7 不同水深条件下桩柱的力学特性（工况14～18） Fig.7 Mechanical properties of piles under different water depths (cases 14-18)

3 结 论

桩柱是桩柱式围网养殖设施的主要结构，主要起到固定网衣的作用。因此，设计和施工过程中对于桩柱结构水平承载力特性的研究是保证整个工程全寿命周期安全运行的前提。本文采用地基反力法中的常数法分析探讨了环境动力（水流、波浪、波流联合、水深）和桩柱埋深对桩柱动力响应的影响规律，得到了桩柱结构在不同工况下的位移、弯矩变化情况，结论如下：

1）单纯水流条件下，桩柱结构位移曲线沿水深方向逐渐减小。海床面以上15 m 至海床面以下5 m 范围内，桩柱结构的位移变化较为显著且随流速增加而增大。第一弯矩零点将整体弯矩分为正、负2 个部分且弯矩值沿着深度方向先增加后减小，最大弯矩值随流速的增加而增大。本组工况下该养殖结构稳定性良好，安全系数高。

2）波浪条件下，随着波高的增加桩柱结构从弹性变形阶段到屈服阶段，桩柱结构的最大位移和最大弯矩均随波高的增加而增大。其中5 m 波高可作为波浪条件下，该养殖结构发生破坏的临界值。当固定波高（5 m）不变时，桩柱结构的最大位移和最大弯矩随水深的增加而增大，随埋深的增加而减小，此时，海床面桩柱露出高度与海床埋深比不大于0.8 为宜。

3）波流联合作用下，桩柱结构同一深度处的位移和弯矩随着波高增大而增大；当波高为3 m、流速为1.0 m/s时，桩柱结构的最大弯矩大于其极限弯矩，在海床面以下2 m 范围桩柱将发生断裂，桩柱结构失稳。

由于桩柱结构尺寸较大且海洋动力环境复杂，在海上开展实测和实例研究难度较大。目前，尚没有针对围网桩柱结构受力特性的现场实测研究报道，也没有专门针对围网桩柱结构受力特性的理论计算研究报道。因此，本文尝试从基础理论出发，计算分析波流作用下围网桩柱结构的受力特性。现阶段，尚没有相关的围网养殖工程桩柱结构设计规范，工程设计阶段大多凭借经验，也因此出现了很多失败的案例。该文研究结果可以明晰海洋环境作用下围网养殖工程桩柱结构的受力特性，进而为新建围网养殖工程的桩柱结构选型和施工提供指导，更可以为未来围网养殖工程桩柱结构设计规范编写提供理论支撑。后续研究可以考虑通过在桩柱上布设应力、位移传感器的方式对围网工程桩柱结构开展长期监测，为未来开展更加深入的研究提供验证资料。