基于稳态特性的路程预瞄转向模型＊

杨浩 魏显坤 黄超群 税永波

（重庆工商职业学院，重庆 401520）

主题词：预瞄距离自适应 稳态转向 路程预瞄 理想转向模型 修正转向模型

1 前言

驾驶员的行为规律对人-车-路闭环系统具有重要作用。目前，驾驶员模型主要分为预瞄驾驶员模型[1-2]、智能控制驾驶员模型[3-5]和仿生物学驾驶员模型[6]3 种。文献[1]基于不同的假设，提出了一类单点预瞄模型；文献[2]基于预瞄远近点的关系，建立了两点预瞄模型；文献[3]将单点预瞄与神经网络相结合，建立了一种预瞄优化神经网络驾驶员模型。文献[4]通过模拟人的推理能力，提出一种模糊控制驾驶员模型；文献[5]基于模型预测控制算法，建立了一种多约束的驾驶员模型。文献[6]基于仿生学特征，建立了一种基于脑情感学习回路的横、纵向综合控制驾驶员模型。上述方法在路径跟踪方面取得了一定进展，但并没有充分反映驾驶员的预瞄行为和车辆是否处于稳态转向特性的理想状态。

郭孔辉院士的研究表明[7]，驾驶员预瞄更一般的形式是其目光不只集中于前方一点，而是着眼于前方一段路，并使汽车在这一段路程内的误差最小，即路程预瞄。本文基于以上分析，寻求出一种稳态转向特性与路程预瞄所满足的理想关系，建立理想的转向盘转角模型，基于车辆在大曲率路径下易处于非线性状态的特性，建立转向修正模型，并利用CarSim/Simulink 进行联合仿真，验证所提出的2 种转向模型路径跟踪的有效性、适应性和精度。

2 预瞄距离自适应模型

假设驾驶员跟踪的目标路径为f(x)，如图1所示，根据f(x)曲率的不同取值，道路路径可分为凸弯道路径弧P0P1″P2、直线路径P0P1′P2、凹弯道路径P0P1P23 种情况。设在可视范围内预瞄f(x)上近、中、远3个点即P0、P1、P2，其对应的侧向误差分别为s0、s1、s2。在预瞄方向xt上预瞄的一小段路程为(xt2-xt0)，G0(xt0,0)、G1(xt1,0)、G2(xt2,0)为预瞄路程上的起点、中点、终点。

图1 预瞄距离自适应模型

驾驶员在路径跟踪时总是力求f(x)在预瞄方向上xt0至xt2的累计误差最小，即路程预瞄的累计误差esum最小：

由于路径跟随时，f(x)相对于车辆是动态变化的，此时用路径规划的方法拟合f(x)有一定难度，同时还存在时间上的滞后性，因此式（1）不易求解，而车辆前方的预瞄点P0(xt0,s0)、P1(xt1,s1)、P2(xt2,s2)可以通过传感器获取。因此，本文采用辛普森法则（Simpson’s Rule）[8]，用数值计算代替积分计算，且能取得5阶高精度。根据辛普森法则可知：

为了判断f(x)属于凸弯道路径、直线路径或凹弯道路径，定义f(x)与预瞄远、近点连线在预瞄方向上围成的面积之差k为：

由图1可得：当f(x)为凸弯道路径弧P0P1″P2时，k＞0；当f(x)为直线路径P0P1′P2时，k=0；当f(x)为凹弯道路径P0P1P2时，k＜0。|k|越大，f(x)相对于预瞄方向的曲率越大，反之亦然。因此，定义k为路程预瞄曲率阈值。

基于真实驾驶员在高速时目光较远，低速时目光较近的情况，建立预瞄距离随路程预瞄曲率阈值和车速可变的自适应跟踪模型。生理、心理学家Land和Horwood对驾驶员在弯道行驶的行为研究表明[9-10]，驾驶员视线集中的范围主要包括“远”（车前方10～20 m）、“近”（车前方6～8 m）2个区域。结合文献[4]，预瞄距离d的自适应公式为：

式中，c为常数，我国高速公路最高车速为120 km/h，当车辆在直线路径（k=0）行驶时，参考Land 和Horwood 的研究成果，c的取值范围一般为6～20，可实现预瞄距离在6～20 m内变化。

3 参考车辆模型

为预测汽车在未来一段时间内的运动轨迹，并使车辆处于稳态转向的可控阶段，以2自由度车辆模型作为参考模型，并假设车辆处于稳态转向，如图2所示。

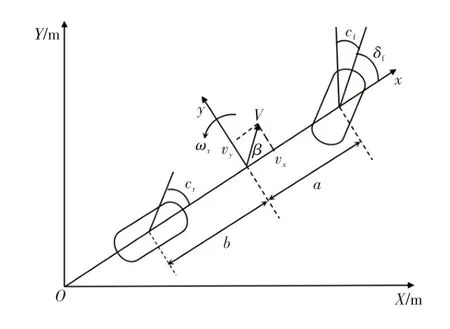
图2 自由度车辆模型

参考模型状态方程可以表示为：

式中，β为质心侧偏角；ωr为横摆角速度；vx、vy为汽车纵、横向速度；δ为前轮转角；Iz为转动惯量；k1、k2分别为轮胎的等效侧偏刚度；a、b分别为质心至前后、后轴的距离；m为整车质量。

式中，isw为转向系传动比；L=a+b为汽车轴距；为汽车稳定性因数。

同理可得，汽车质心侧偏角β对转向盘转角δsw的稳态增益为：

车辆在运动过程中的侧向加速度为：

4 2种基于路程预瞄的轨迹预测转向模型

4.1 理想模型

假设汽车做稳态转向运动，即在预瞄距离d内横摆角速度ωr与速度V保持不变，那么汽车在未来一段时间内将做匀速圆周运动，速度方向与行驶轨迹相切，如图3所示。其中，G0为车辆质心，车辆的运动轨迹为圆O的一段弧G0T，R、θ分别为圆弧对应的半径与圆心角，T、Q分别为预测轨迹和速度方向在侧向误差s2上的交点，yG2T为车辆行驶预瞄距离d后所处的侧向位置，Δf为其与预瞄点P2的侧向误差。

图3 稳态转向的车辆轨迹预测

由图3的几何关系易知：

式中，tp为预瞄时间。

驾驶员在路径跟随过程中，力求侧向误差最小，即Δf接近于0，此时行驶轨迹的T点与期望的目标路径P2点重合。将式（6）与式（7）带入式（11）可得：

由此可得期望的转向盘转角为[1]：

式（13）仅实现了单点预瞄的误差最小，这与真实驾驶员的跟随行为不符，因为真实驾驶员往往使预瞄视线内的整段路径累计误差最小，即跟踪轨迹与f(x)趋于重合。假设存在某一函数值f*(x)，使其在预瞄距离d上构成的面积等于f(x)在预瞄距离d上所围成的面积，则可用其代替式（13）中的yG2T，实现将单点预瞄模型转化为路程预瞄模型。根据积分第一中值定理性质可得：

将式（2）带入式（14）得：

由此可以得到一种预瞄距离自适应的路程预瞄跟踪模型的转向盘转角为：

① 计算类别信息熵：类别（决策）属性为“救治方案”，该属性分为 3 类：F1、F2、F3。F1（一般处理）＝11，F2（常规治疗）＝7，F3（紧急救治）＝2，F＝F1＋F2＋F3＝20。计算公式为：

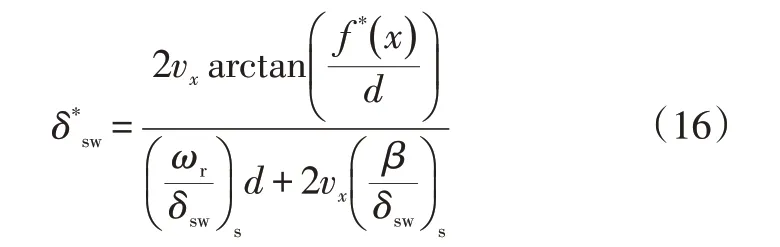
此转角基于稳态转向和侧向误差为零的理想状态求得，因此称为理想模型。

4.2 修正模型

基于车辆动力学特性、轮胎的非线性和驾驶员反应滞后等因素，Δf一般不为零。因此，有必要建立以车辆运动轨迹为基础的侧向偏差修正模型。

车辆做匀速圆周运动，则有R=V/ωr，由图3可知：

在Rt △TG2G0中：

在△OG0T中，由余弦定理得：

综合式（17）～式（20）可得：

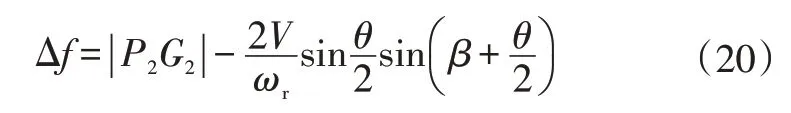
式（20）中，P2G2仅为单点预瞄的侧向误差，与实际路程预瞄不符，因此用f*(x)代替P2G2，将单点预瞄转化为路程预瞄：

式（21）中|f*(x)|可通过车身传感器获取的f(x)预瞄点的坐标求解，为基于车辆实际运动状态求解的侧向位置yG2T的等效表达式。因此，Δf*为基于路程预瞄的实际侧向误差。Δf*在加速度恒定时产生且较小，因此，可以将实际侧向误差轨迹用直线近似代替，并借助匀加速直线运动来修正：

将式（9）带入式（22）可得消除Δf*所对应的转向盘转角为：

综上，修正后的转向盘转角为δ*sw与δΔsw之和：

由式（21）可知，由于存在分母项ωr，易造成式（24）在ωr为零时Δf*取值发散，且在直线路径行驶时车辆的ωr很小或趋近于0，在弯道路径时ωr较大。结合k的取值，可建立逻辑门限控制条件：

以上转向盘转角模型是通过理想转向盘转角与侧向误差对应的转向盘转角之和修正所得，因此称为修正模型。

2种模型的流程如图4所示。

图4 2种基于稳态特性的路程预瞄驾驶员模型

5 仿真验证

为测试本文提出的2 种转向模型路径跟踪的有效性、适应性和精度，基于CarSim 与MATLAB/Simulink 构建的联合仿真平台进行验证。该仿真平台由CarSim提供车辆动力学模块，即CarSim-S 函数，在Simulink 中搭建算法，并将仿真结果与CarSim 软件的转向模型进行对比分析。仿真参数如表1所示。

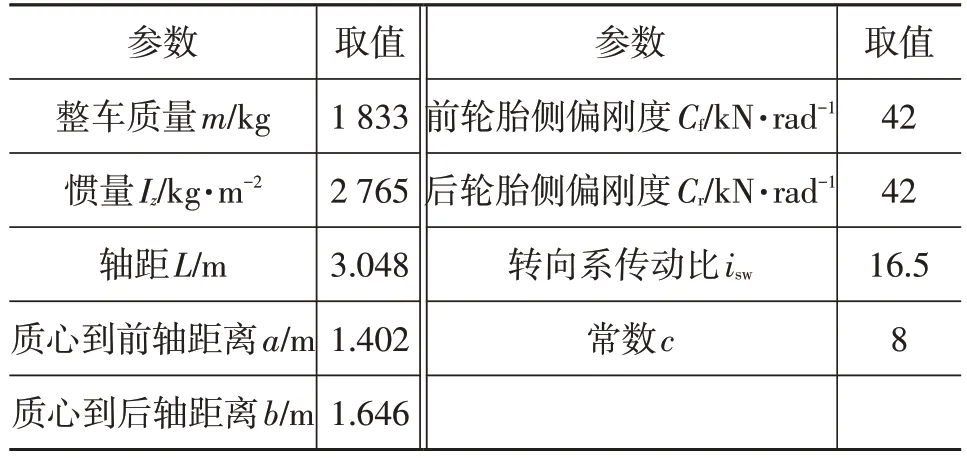
表1 仿真参数表

5.1 复杂路径跟踪

为验证不同曲率路径上车辆的跟踪效果，选取半径不同的10 个弯角路径（即复杂路径）进行跟踪，真实驾驶员在危险工况、极限条件和复杂路径时往往采用低速行驶，因此，设置车速为60 km/h 进行验证，结果如图5所示。

图5 复杂路径仿真结果

由图5a可知，3种转向模型的跟踪轨迹与目标路径趋于重合，表明3 种驾驶员模型均具有较好的跟踪效果；由图5b可知，CarSim模型、修正模型、理想模型分别形成从大到小的误差包络曲线。由图5c 可知，CarSim模型的转向盘转角在160 m处附近发生了200°～300°较大波动，修正模型在-100 m、0 m、200 m、300 m 的弯道处均发生了小幅度振荡，说明弯道处的转向盘转角修正过程可以避免其大幅度波动。理想模型转向盘转角曲线趋于平滑且无振荡，表明转向平稳。

5.2 “8”字形路径跟踪

为了验证大曲率急转弯时的跟踪有效性和转向轻便性，选取“8”字形路径进行跟踪，这种路径特别适合转向轻便性评价[8]，并以80 km/h 车速进行验证，结果如图6所示。

图6 “8”字形路径仿真结果

由图6a可知，3种转向模型的跟踪轨迹与目标路径趋于重合，表明3 种驾驶员模型均具有较好的跟踪效果；由图6b可知，理想模型和修正模型较CarSim模型有更好的跟踪效果和跟踪精度，且理想模型的效果最好。由图6c 可知，理想模型和修正模型转向盘转角在-60～20 m、0 m、40～80 m 的弯道处均发生了小幅度振荡，说明弯道处的转向盘转角修正过程可以避免转向盘转角和侧向误差的大幅度波动。

5.3 双移线路径跟踪

为有效验证控制算法的动力学特性和转向控制的综合能力，跟踪路径选择双移线路径，双移线路径测试是车辆稳定性能测试项目，包括转向角快速逆转的激烈转向路线测试，可以在一定程度上表现出汽车转向运动的综合能力[11]。测试以100 km/h 车速进行，结果如图7所示。

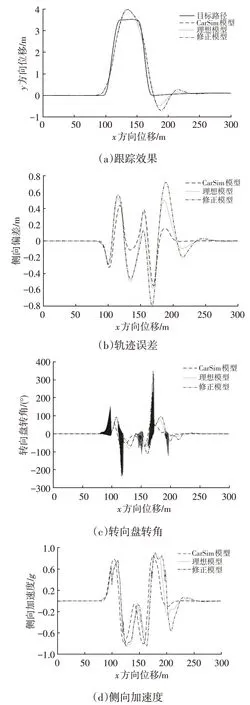
图7 双移线路径仿真结果

由图7a 可知，理想模型与修正模型的跟踪轨迹较CarSim模型在130 m、180～240 m处出现了较小波动，其中理想模型较修正模型更小。由图7b 可知，理想模型和修正模型较CarSim模型的跟踪效果和跟踪精度均有所降低。由图7c 可知，理想模型转向盘转角较修正模型振荡幅度更小，CarSim 模型转向曲线趋于平滑，从转向平顺性来分析，CarSim模型最优，理想模型次之，修正模型较前两者差。由图7d可知，3种模型的侧向加速度变化曲线趋于一致，且均超过0.4g，表明车辆状态已经进入非线性区域，轮胎侧偏力接近饱和，使与真实值不匹配，导致理想模型和修正模型的跟踪效果和跟踪精度有所降低。

5.4 Alt3路径跟踪

为验证高速公路的跟踪效果，跟踪路径选择美国Alt3 高速路径，以120 km/h 车速进行验证，结果如图8所示。

图8 Alt3路径仿真结果

由图8a可知，3种转向模型的跟踪轨迹与目标路径趋于重合，表明3 种驾驶员模型均具有较好的跟踪效果；由图8b可知，理想模型和修正模型较CarSim模型的跟踪效果和跟踪精度有略有下降。由图8c可知，3种模型转向盘转角变化趋势趋于一致且无振荡，表明3种模型均具有较好的转向平顺性。由图8d可知，3种模型的侧向加速度变化曲线趋于一致，且取值均在-1g～1g范围内。由于数值已经超过临界值0.4g，表明车辆状态已经进入非线性区域，且轮胎侧偏力接近饱和，使与真实值不匹配，进而导致理想模型和修正模型的跟踪效果和跟踪精度有所降低。

6 结束语

本文建立了稳态转向特性与路程预瞄转向模型所满足的理想关系，并兼顾了路径跟踪的精度和跟踪时的车辆稳态特性。实现了预瞄距离的自适应，并将单点预瞄转化为路程预瞄，分别建立理想转向模型和修正转向模型。通过仿真可知，理想模型和修正模型较CarSim 模型表现出更好的适应性和跟随精度。在整体路径跟踪过程中，理想模型较修正模型表现出更好的综合优势。

由于线性修正对车辆的非线性并未取得较理想模型更优的跟随效果，使得横摆角速度、质心侧偏角、侧向加速度分别对转向盘转角增益值与真实值不匹配，导致跟踪精度有所降低，这是本文需要改进的方向。基于车辆的非线性特性，可以尝试用实际侧向加速度与稳态侧向加速度的差值来修正。