两个种群生态系统最优响应算法及其收敛性

从艳芳，王祝君

（1.福州大学 数学与计算机科学学院，福州 350000；2.湖南工程学院 计算科学与电子学院，湘潭 411104）

0 引言

种群是指在特定时间和空间中生活和繁殖的同种个体的总和.在同一空间，两个群体之间有竞争、合作、替代等关系.两个种群的种群功能类似，但是彼此提供能源的方式、技术以及数量不尽相同，双方给环境带来的影响也不同.两个种群之间相互抑制，又互相促进，受各种复杂关系的制约，要想获得种群在特定时刻的准确分布数量或者密度值，往往相当困难.但是，研究与其等效的稳定状态的数量或密度关系，却有着重要的理论与应用价值.对于种群关系的研究，大多是建立在Lotka-Volterra模型［1-2］的基础上，通过分析常微分方程的稳定性，研究不同条件下种群的食饵模型达到稳定状态的情况.

自从Nash［3-4］对非合作博弈提出了一种被称为Nash均衡解的概念之后，如何找到非合作博弈的Nash均衡已成为一个非常经典的问题.Nash均衡问题是经济学和管理学等的基础，在计算机工程，生物信息学等各个领域也有着广泛的应用［5-7］.本文从博弈论角度研究两个种群生态系统的最优响应算法及其收敛性，即将两个种群竞争模型当作一个博弈模型，设计一个最优响应算法，证明算法收敛于Nash均衡解.

1 问题描述

自然界中任何一种物种都不是孤立存在的，总是同其他物种发生这样或那样的关系.物种之间的相互作用关系对于整个生物界的生存和发展是极其重要的，这种作用关系将各个物种连接为一个复杂的生命之网，决定着群落和生态系统的稳定性.不同种群之间存在着一种相互依赖、相互制约的生存方式，如种群甲靠丰富的自然资源生长，而种群乙靠捕食种群甲为生，生态学上称种群甲为食饵，种群乙是捕食者，二者共处组成捕食者-食饵系统.由于生物的很多适应性都可以用捕食者和食饵之间的协同进化加以说明，所以对于捕食者-食饵相互作用关系的研究具有非常重要的理论意义和应用价值.在这里我们仅以文献［8］中经典的Lotka-Volterra模型为例.两个种群竞争模型为：

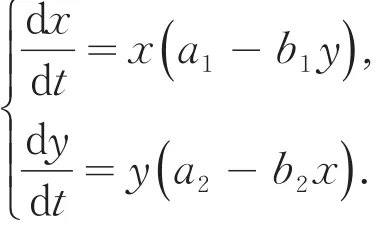
设θ1(x ,y )，θ2(x ,y)分别表示两个种群的数量，则：

用博弈模型来表达同一生态系统中两个具有竞争关系的种群平衡问题，我们得到

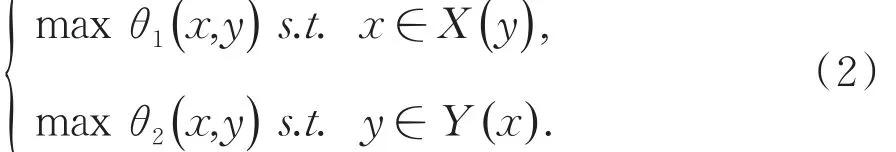
在有限资源环境下，种群数量随着时间动态地逼近均衡状态，因此有

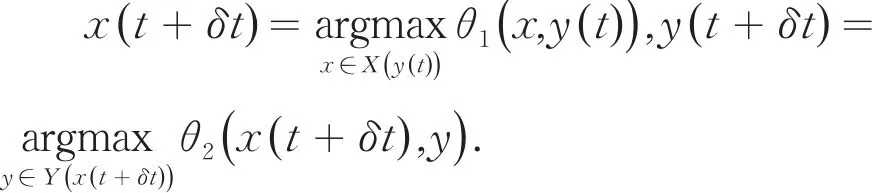
由Nash均衡的定义知，w*=(x*,y*)∈X×Y是上述博弈的一个Nash均衡解，当且仅当x*=

2 投影梯度法

给出一些符号说明：对任意的x∈Rn，‖‖x定义为x的Euclidean范数，即定义为x的椭球范数，即‖x ‖=xTGx，G ∈ Sn+；在闭凸集Ω上的投影算子定义为

2.1 临近型线性化迭代算法

因为 θ1(x ,y )，θ2(x ,y)均为未知，直接求解（2）具有一定的困难，根据种群的生态系统模型可知，∇xθ1(x .y)=f(x ,y )，∇yθ2(x .y)=g(x ,y).因此，我们可采用临近型线性化迭代方法得到：

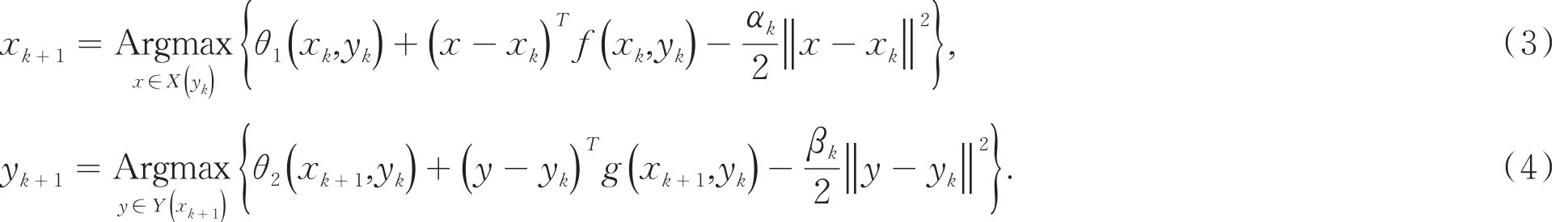
对于非合作博弈的Nash均衡问题，常见的求解算法包括正则化Gauss-Seidel算法、信赖域算法等［9］.Zhang等［10］借助预测-校正的思想，提出了通过投影算法获得博弈的广义Nash平衡点，Peng等［11］将两人轮流博弈问题转变成求解变分不等式问题，在预测-校正过程中利用非精确的临近点交替方向法求得Nash平衡点.对于运用预测和校正两个步骤来求解博弈问题，相当于对于博弈的策略进行了外界因素的调整，在自然环境下食物链适应于“物竞天择，适者生存”法则，排除人为因素的影响.针对这种不允许校正的非合作博弈Nash均衡来说，本文提出一种投影梯度算法，并在一定条件下证明算法全局收敛到Nash平衡点.

全文通篇做如下假设：

假设1两种群的数量函数θ1(x ,y )，θ2(x ,y)都是自身控制的可微凹函数，即：对于任意固定y，θ1(x ,y)是x∈X(y)⊂Rn的可微凹函数；对于任一固定的x，θ2(x ,y)是y∈Y(x)⊂Rm的可微凹函数.

由 模 型（1）知 ，∇xθ1(x .y)=f(x ,y )，∇yθ2(x .y)=g(x ,y).根据假设1，任意给定y，f(x ,y)关于x∈X(y)单调.同样，任意给定x，g(x ,y)关于y∈Y(x)单调.故：

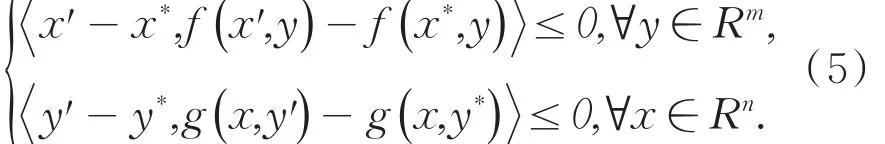
假设2决策集X、Y是简单的有界闭凸集，以保证其在闭集上的投影比较容易计算.在上述假设条件下，两种群博弈的Nash均衡解等价于下列变分不等式组的解：

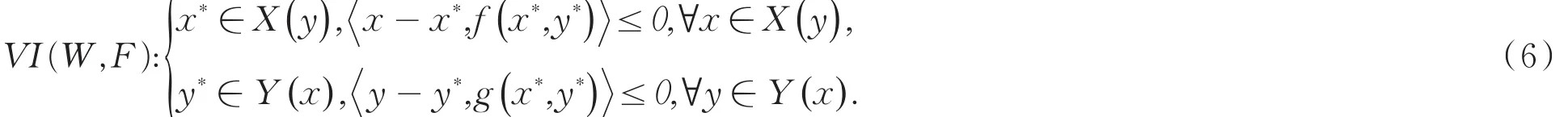
这种等价性提示，可以借助变分不等式的求解方法来计算博弈的Nash均衡解，本文用投影梯度的方法求解变分不等式问题.迭代（3）和（4）等价于：

2.2 算法描述及收敛性分析

本节先给出一种求解两个种群的生态系统博弈Nash均衡问题的最优响应算法，然后对算法的全局收敛性进行分析.

算法1最优响应算法

步骤1初始化，令ε＞0，对任意给定的初始点x0∈X，X ⊆Rn，Y ⊆Rm，通过求解问题得到y1∈Y：y-y1,g(x0,y1)-β0(y1-y0) ≤ 0,∀y∈ Y(x0).

步骤2对于给定的(xk,yk)，分别求解如下的变分不等式，得到当前情况下的最优策略：xk+1∈X(yk)和yk+1∈Y(xk+1)：

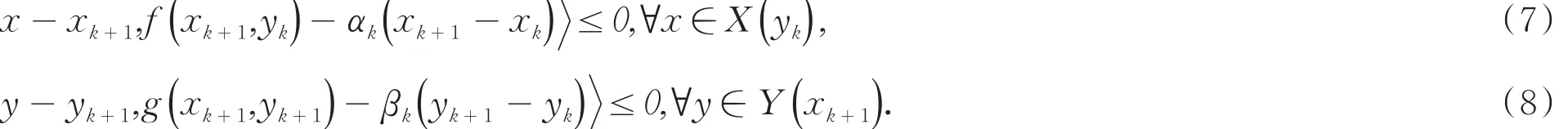
步骤3计算εk=max{‖ xk+1-xk‖,‖yk+1-yk‖}，如果εk＜ ε，则停止.否则，令k:=k+1，返回步骤1.

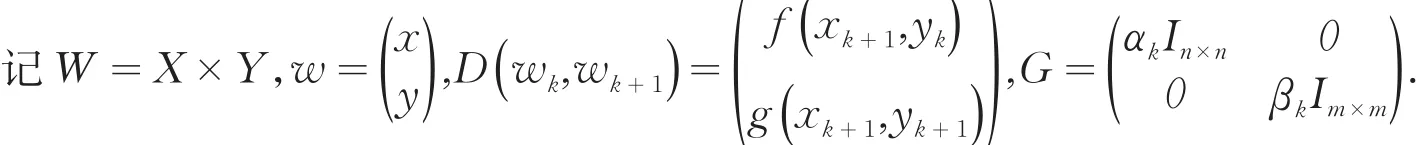
则迭代（7）和（8）可以写成下列的紧凑形式：求wk+1∈W，使得

假设3若w*=(x*,y*)∈W是博弈的一个Nash均衡点，则

引理1对于给定的wk，设wk+1是由算法1产生新迭代点，若

w*=(x*,y*)∈W是种群博弈问题的一个Nash均衡点，则

证明.由f(x ,y)，g(x ,y)的单调性，将(x ′,y′)=(xk+1,yk+1)代入式（5）

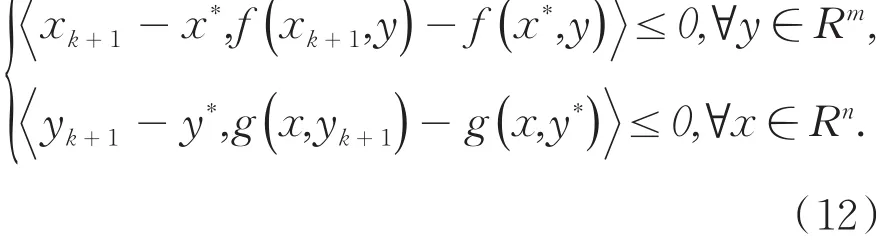
将(x ,y)=(xk+1,yk)和(x ,y)=(x*,y*)分别代入（12），将两式相加求和，得到：

把(x ,y)=(xk+1,yk)和(x ,y)=(xk+1,yk+1)分别代入式（10）的第一个和第二个不等式并结合式（6），（12）和（13），直接得到式（11）.证毕.

定理1设{wk}是算法1产生的迭代序列，w*是所考虑的种群博弈模型的一个Nash均衡点，则

证明将w=w*，代入（9）可得

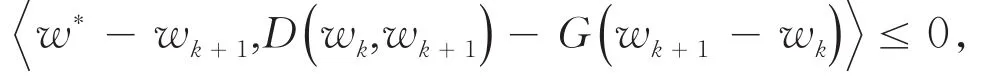
展开得到 w*-wk+1,D(wk,wk+1) ≤

(w*-wk+1,G(wk+1-wk))，所以

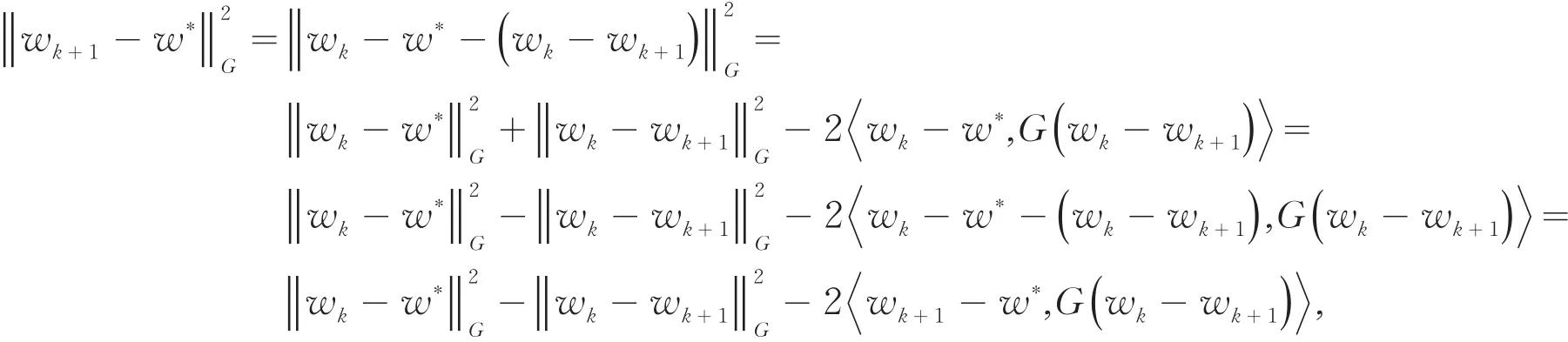
再结合上式和引理1可以直接得到（14），定理得证.

定理2算法1产生的迭代序列{ }wk收敛于Nash均衡点.

证明.由定理1可得

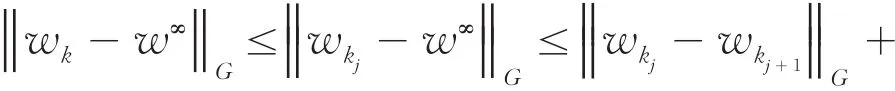
3 结论

本文研究种群动力学中捕食者-食饵模型的Nash均衡问题，即在有限资源环境下，种群数量随着时间动态逼近均衡状态.建立了两个种群竞争博弈的Nash均衡模型，采用交替投影梯度算法求解所得的博弈模型，证明了所提出的算法收敛到该博弈的Nash均衡点，即两种群竞争生态系统的均衡点.