碰撞悬臂梁系统的混沌控制
赵 锐
(商洛学院 数学与计算机应用学院, 陕西 商洛 726000)
碰撞悬臂梁是一种非光滑系统,经常出现在工程和物理问题中.近年来,该系统受到了显著的关注.文献[1-4]给出了关于这种系统的一些重要的结论.由于受到碰撞的影响,使得该系统能产生一些有趣的非光滑动力学行为,例如一些独特的混沌[1-3].然而在实际中,有时更需要有规律的行为,因此针对这种非光滑系统的混沌控制具有重要意义.
在过去的几十年中,许多方法已经被用来实现混沌控制,例如OGY控制法[5]、反馈控制法[6]和脉冲控制法[7-8]等.后步控制法是另外一种重要的混沌控制方法[9-10],其控制法则可以通过Lyapunov 稳定性理论推导而得到.后步控制法已经被成功应用于对Lorenz 系统、Chen系统和Lü系统的混沌控制[9-10].在文献[11]中,此方法被用来对碰撞振动系统进行混沌控制,控制的策略是根据系统的输出来设计控制器.后步控制技术不仅可以驱动混沌吸引子成为稳态,同时还可以将其控制到期望的轨道.
笔者使用后步控制策略对碰撞悬臂梁系统进行混沌控制,将系统的输出在其定义域范围内控制到任意期望的轨道.首先给出系统的控制策略,并得出相应的控制器,然后进行数值模拟,验证该策略的有效性.
1 基于后步控制法的碰撞悬臂梁系统混沌控制
考虑图1所示的碰撞悬臂梁系统
长方体的质量为m,悬臂梁的长度和弯曲弹性系数分别为l和EI,弹簧的弹性系数为k,长方体与弹性支撑面的距离为g,在F(t)=F0cosωt的激励下,长方体的位移为x.该系统的动力学方程可表示为[1-2]
(1)
其中,H(x)是如下的Heaviside函数

(2)

为了方便下面的讨论,以如下的无量纲形式重写方程为[1]

(3)
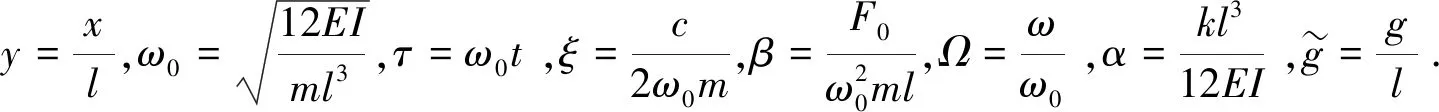
由文献[1-4]知,PWL和PWN系统都可以容易地产生混沌吸引子.将分别针对PWL和PWN系统使用后步策略设计控制器,将系统的的输出控制到期望的轨道.
1.1 分段线性(PWL)系统的控制首先,把PWL系统重新表示为以下形式

(4)
为了控制该系统,在系统(4)的第二个方程中加入控制器u1,可以得到一个可控制的系统,即
(5)

(6)

(7)



(8)
(9)
(10)
显然,令ξ>0且
(11)
可使 (10) 负定.

(12)
(13)
同时,V2在系统(13)上的时间导数为
(14)
令ξ>0且
(15)
可使方程 (14) 负定.
因此得到受控PWL系统的控制器为
(16)
在此条件下,系统(9)和(13)在初值(0,0)处稳定,即PWL系统的输出被稳定在r(τ).
1.2 分段非线性(PWN)系统的控制将PWN系统改写为
(17)
对系统(17)的第二个方程增加一个控制器u2,可得如下的受控系统
(18)

(19)

(20)


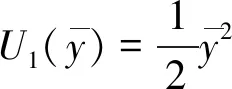
(21)
(22)
(23)
令ξ>0且
(24)
便使系统(23) 负定.
迭代上述过程, 可以得到此条件下的控制法则, 即ξ>0且
(25)
可以给出受控PWM系统的控制器如下
(26)
方程(26)可以保证PWN系统的输出y被控制期望的轨迹r(τ).
2 数值模拟

假设期望的轨道为r(τ)=0.5 sin(τ),当τ=80时打开由式(16)得到的控制器u1,此时PWL系统的输出y如图3所示.图4给出了r(τ)=0.2 sin(0.5τ),当τ=120时打开控制器,受控PWL系统的输出.基于这些模拟,可以发现给出的PWL系统的控制规则是非常有效的.


图2 PWL系统的混沌吸引子图3 r(τ)=0.5sin(τ)时受控PWL系统的输出控制到目标轨道
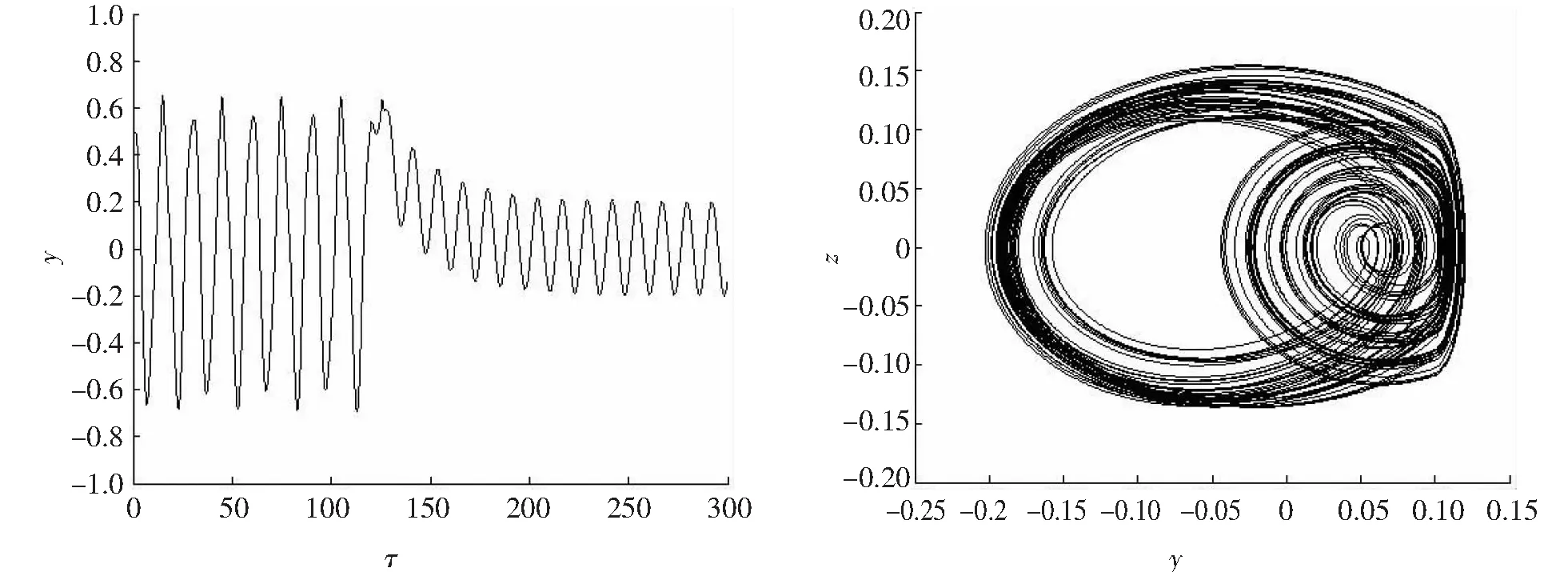

图4 r(τ)=0.2sin(0.5τ)时受控PWL系统的输出控制到目标轨道图5 PWN系统的混沌吸引子


图6 r(τ)=0.1sin(τ)时受控PWN系统的输出控制到目标轨道图7 r(τ)=0.05sin(0.5τ)时受控PWN 系统的输出控制到目标轨道
假设期望的轨道为r(τ)=0.1 sin(τ),当τ=80时打开由方程(17)求出的控制器u2,图6给出了受控PWN系统的输出.期望轨道r(τ)=0.05 sin(0.5τ),当τ=120时打开控制器,受控PWL系统的输出y如图7所示. 图6和图7的结果验证了关于PWN系统的控制规则的有效性.
3 小 结
给出了一种基于Lyapunov稳定性理论的后步控制方法用于实现悬臂梁系统的混沌控制. 根据系统的特点,控制器被设计为分段函数,导出的控制器可以将系统的输出在其定义域范围内控制到任意期望的轨道上,数值模拟验证了控制策略的有效性.

