一维对流弥散方程的显式差分法求解及其收敛性分析
(石家庄铁道大学 土木工程学院,河北 石家庄 050043)
1 研究背景
在滨海及海岛地区,由于地下水的超量开采,海水入侵已经成为沿海地区普遍面临的重大地质灾害之一。自20世纪70年代以来,国内外对海水入侵进行了大量研究并取得很大进展,其中数学模型的研究是其中的重要方面之一,而对流弥散模型能够较好地模拟和解释海水入侵问题[1]。研究一维对流弥散方程是研究海水入侵的重要方法,能够粗略地模拟出海水入侵情况,相比较二维和三维所需要的参数较少,是一种简易可行的方法。杨金忠[2]对各种求解对流弥散方程数值方法比较,认为对于一维问题,有限差分法能够得到精确结果,因此本文提出利用显式有限差分法对一维对流弥散模型进行求解,具有操作简单、稳定性和收敛性好的特点,是求解一维对流弥散模型的有效方法。
有限差分法是一种古典的数值计算方法。随着数值计算方法的研究和发展,差分法已经被广泛应用在地下水渗流问题和浓度扩散问题中。其基本思想是:用渗流区内有限个离散点的集合代替连续的渗流区,在这些离散点上用差商近似地代替微商,将微分方程及其定解条件化为以未知函数在离散点上的近似值为未知量的代数方程(称为差分方程),然后求解差分方程,从而得到微分方程的解在离散点上的近似值。有限差分法难免会产生截断误差、舍入误差和测量误差,如果在某个节点某个时阶处出现误差后,会对下一步的迭代求解过程产生影响,是误差逐渐变小还是被无限放大,需要讨论差分法的收敛性和稳定性[3-4]。
夏源等[5]提出分数阶对流弥散方程的数值求解方法,杨淑伶[6]提出求解分数阶对流弥散方程的边界值法。传统研究对流弥散方程的数值求解时,往往将纵向弥散系数看做常数,而事实上纵向弥散系数与流速的大小成正比,当流速在空间的分布不相等时,流速和纵向弥散系数均不能看做常数。在研究对流弥散方程的差分法求解时,在不同渗流方向下,流速会与盐分迁移的方向相同或相反,代入到差分式当中会有正负号的影响,而弥散系数只与流速的大小有关,为保证迭代式中的流速项系数为正值,在不同的渗流方向下,对流弥散方程会出现2种差分迭代式,这是以往研究没有考虑到的。
当利用有限差分法求解一维对流弥散方程时,需要考虑边界条件的问题,李新洁等[7]采用Dirichlet零边值边界条件求解对流弥散方程。本文引入边界衰减因子来解释盐分在边界处存在稀释和衰减的情况,并讨论在不同渗流方向下的影响,最后讨论了在不同渗流方向下给出不同的差分式,并给出了各自对应的收敛条件,在收敛条件下,利用显式差分法求解对流弥散方程是收敛的。
2 研究方法
2.1 一维对流弥散方程
以一维对流弥散方程为研究对象,不计源汇项,且孔隙率n为常数,在稳定渗流场中,若求解对流弥散方程得出溶质浓度变化引起的水密度变化可以忽略,则水流方程和溶质迁移方程可以独立求解。由水流方程的解得出研究区域及时段的速度分量,然后把速度作为输入代入对流弥散方程。这种“去耦”法计算效率高[8]。
(1)
(2)
Dl=αL|Vx|+D*
(3)
式中,k为渗透系数;Dl为弥散系数,为反映可溶性物质通过渗透介质时的弥散现象强弱的物理量;αL为纵向弥散度;D*=τD0,τ为孔隙介质的弯曲度,取值范围为0.5~0.01,D0为开放水体的分子扩散系数,对于NaCl盐溶液经查表得D0=1.48×10-5cm2/s[9],τ取0.5,代入得到D*=7.4×10-10m2/s,其值太小可忽略不计。
Dl=αL|Vx|
(4)
2.2 划分网格
在海水入侵模型中,假设左侧海水高度为h0,右侧淡水水头为hN,渗流区间[0,L]均匀分布N+1个节点,则空间步长Δ=L/N,X0=0,节点号数x乘以空间步长Δx便是该节点距左侧海水边界的长度,lxi=iΔ(=1,2,…,N);取时间步长为Δt,则tn=nΔt(n=1,2, …,M)。
2.3 微分方程的显式差分化
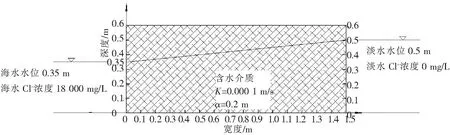
对于一维海水入侵对流弥散模型,存在2种类型,正向渗流类型是左侧海水水位高,右侧淡水水位低,即h0>hN,如图1所示,此时速度方向与盐分迁移的方向相同,且与x轴方向相同;逆向渗流类型是左侧海水水位低,右侧淡水水位高,即h0 在正向渗流的类型下,流速为正值,根据达西定律,待到稳定后,Vi的值和hi存在一一对应关系,根据空间节点处流量相等的原理[10],可以求得稳定后的流速表达式为 (5) (6) (7) (8) 将一维对流弥散方程式(1)差分化为 (9) (10) 对式(10)进行恒等变换有 (11) 令 (12) 则可化简为 (13) 式(13)代表一维对流弥散方程在正向渗流类型下的显式差分迭代公式。 在逆向渗流的情况下,代入流速的计算值为负值,考虑到弥散系数不随流速正负的影响而只与大小有关,为了保证代入的显式差分式中的流速项系数为正值,故将式(1)差分化为 (14) 当i=N时,浓度的差分式与式(10)相同,且此时的速度表达式为 (15) (16) 同理化为标准的差分式为 (17) 式(17)代表一维对流弥散方程在逆向渗流类型下的显式差分迭代公式。 前面建立差分方程时,是用差商代替微商,在数值法中提出一种差分格式,需要了解其收敛性。 记 (18) 2.4.1 正向渗流类型的收敛条件 当为正向渗流类型时,左侧海水水位高于右侧淡水水位,根据式(10)得到 (19) 令 (20) 有 (21) 当满足 (22) 根据绝对值不等式有 (23) 当第一种类型下,Vi>Vi-1,故有 (24) 如此类推,对于某个时刻tM有 (25) (26) 2.4.2 逆向渗流类型的收敛条件 当为逆向渗流类型时,左侧海水水位低于右侧淡水水位,根据式(14)得到 (27) (28) 当满足 (29) 根据绝对值不等式 (30) 假设存在一个渗流槽,用于模拟海水入侵,槽长L=1.5 m,宽B=0.1 m,高0.6 m,内部填充满含水介质,K=0.000 1 m/s,αL=0.2 m,左侧为定水头和定浓度边界,左侧海水水位为0.5 m,左侧海水初始 离子浓度为18 000 mg/L;右侧为定水头边界,右侧淡水水位为0.35 m,且边界衰减因子为β,此情况属于正向渗流类型,其示意图见图3。取Δx=0.03 m,Δt=100 s,求经过一定迭代次数后,在渗流槽中海水盐分扩散后稳定的浓度与扩散距离的关系。初始及边界条件为 图3 正向渗流类型下渗流槽尺寸及边界条件示意图 图4 正向渗流类型下最终浓度随渗流距离的变化情况 采用有限差分法计算上述算例,在满足收敛条件的情况下,经过6 000步迭代次数后,得到节点位置的浓度基本上不随迭代次数的增加而改变,则绘制最终浓度随渗流距离变化的曲线图,并比较边界衰减因子β=0与β=1的情况,如图4所示。 在正向渗流的情况下,右边界处浓度的衰减对最终稳定状态的影响是比较大的,不能忽略。 当左侧海水水位为0.35 m、右侧淡水水位为0.5 m时,其他条件均与上述情况相同,此情况为逆向渗流类型,其示意图见图5。采用有限差分法计算上述算例,绘制最终浓度随渗流距离变化曲线图,并比较边界衰减因子β=0与β=1的情况,如图6所示。 图5 逆向渗流类型下渗流槽尺寸及边界条件示意图 图6 逆向渗流类型下最终浓度随渗流距离的变化情况 在逆向渗流的情况下,右边界处浓度的衰减对最终稳定状态的影响可忽略不计。 利用显式有限差分法求解一维对流弥散方程的数值解,并结合2种不同渗流方向的类型,给出了相应的显式差分式,推导了各自应满足的收敛条件,且通过实际案例进行算法演示,求解了浓度扩散数值,最后探讨了在不满足收敛条件的情况下的数值特性。计算结果表明: (1)对于2种不同的类型,其有限差分的迭代关系式是不同的,要根据海水入侵的速度方向确定属于什么类型,选择相应的迭代关系式,且要预先计算出流速场,流速场采用本文介绍的计算式算出,然后试代Δx和Δt的值,判定是否满足收敛条件,根据收敛条件选择适当的时间步长Δt和空间步长Δx。Δx和Δt的值越小则截断误差越小,计算的结果精确度越高,但相应的计算量和迭代次数会增加,在满足收敛条件下,适当地提高Δt的值会大大减少迭代次数。采用显式差分法求解一维对流弥散问题,经过一定的迭代次数后,发现数值稳定了,或者误差在允许范围内,所得到的最终结果便是经过相应时间扩散后的浓度,只要满足相应的收敛条件,其计算结果是收敛且误差较低的。 (2)在正向渗流的类型下,右边界处浓度的衰减对最终稳定状态的影响是比较大的,不能忽略。在逆向渗流的类型下,右边界处浓度的衰减对最终稳定状态的影响可忽略不计。 (3)本显式有限差分法能够实现对一维海水入侵对流弥散问题的求解,以往对一维对流弥散方程的求解并没有讨论正向和逆向渗流的情况,讨论在2种不同渗流方向下发生盐分迁移,利用本文所述方法能够计算出各自稳定的浓度情况,原理简单易操作,且能够方便了解每一迭代步内的浓度空间分布情况,更直观研究每个迭代步内的浓度变化规律,是求解海水入侵问题的有效方法。2.4 差分格式的收敛性判定



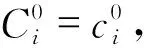
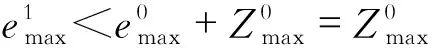
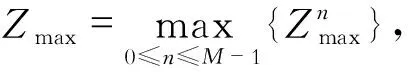
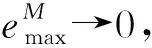
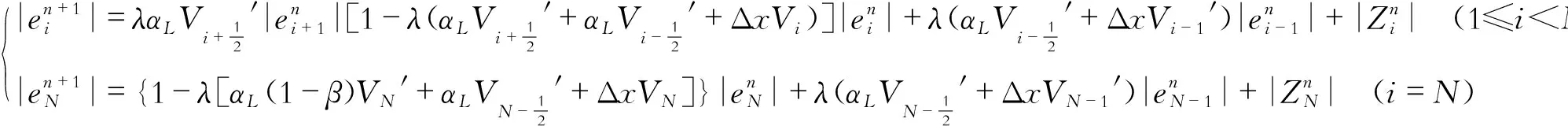
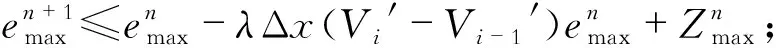

3 数值算例
3.1 正向渗流算例



3.2 逆向渗流算例

4 结论

