针对旅行商问题的改进循环交叉算子遗传算法
郑培豪
(四川大学电子信息学院,成都610065)
0 引言
遗传算法(Genetic Algorithm,GA)最初是由J. D.Bagley 在1967 年提出的,该算法是一种基于达尔文生物自然选择和遗传机制的随机搜索算法,随着大量学者多年的研究和发展,GA 依然成为了无数著作中使用的最通用的全局优化求解方法之一[1]。遗传算法属于仿生启发式算法,具有良好的扩展性、强大的全局搜索能力、容易与其他算法结合的特点,在旅行商问题、全局优化问题、规划调度问题中有这广泛的应用。Ahmed[2]提出了一种新的顺序建设性交叉算子,为TSP生成了高质量的解决方案。Nagata 和Soler[3]提出了一种新的非对称TSP 遗传算法。Deep 和Adane[4]针对顺序交叉算子提出了改进的树形结构。Kumar 等提出了TSP 不同交叉算子的比较分析,并表明部分映射的交叉给出了最短的路径[5]。Liu[6]提出改进的遗传算法,通过对变异操作进行增强突变,在交叉操作中使用异构配对选择代替随机选择,最终在解决TSP 问题时其效果优于传统的遗传算法。葛[7]提出一种染色体择优策略,有效减少了算法陷入局部最优的情况。胡[8]结合了遗传算法的全局搜索能力和蚁群算法的反馈机制,并验证了其算法相较于单遗传算法和蚁群算法有更好的寻优能力。Ma[9]最后,基于遗传算法框架和2-opt 选择策略,提出了一种混合遗传算法。仿真结果表明了该算法的有效性。杨[10]提出了一种改进单亲遗传算法进行路线优化,提高了计算效率。朱[11]对单亲遗传算法进行了递阶式编码相比于普通单亲遗传算法收敛精度提升40%。
1 遗传算法及经典交叉算子
遗传算法是模拟自然进化过程来搜索全局最优解的方法。从一组随机生成的初始解(称为种群)开始搜索过程。其中每一个在种群内的个体都称为染色体(个体),它可以是多种不同的编码形式,现实意义代表着问题的一个解。在种群的繁衍过程中染色体会被遗传到子代中并在遗传过程中发生一些变异。在每一代种群中,适应度被用来衡量度个体的质量。下一代染色体被称为后代。后代是通过上一代染色体的杂交或变异而形成的。在形成新一代的过程中,将根据后代适应度的大小进行筛选,一些适应度较小的将被淘汰,以便保持种群规模不变。适应度高的染色体被选择的概率较高,因此经过几代后,算法收敛到最佳染色体,这可能是问题的最优解或次优解(算法流程如图1)。在遗传算法中,交叉算子和染色体变异是最为重要的两个遗传操作,对种群的丰富性、后代合理性有着重要的影响,本文以交叉算子为研究对象,通过对交叉算子的改进来提升算法的整体性能。图1 为遗传算法流程图。
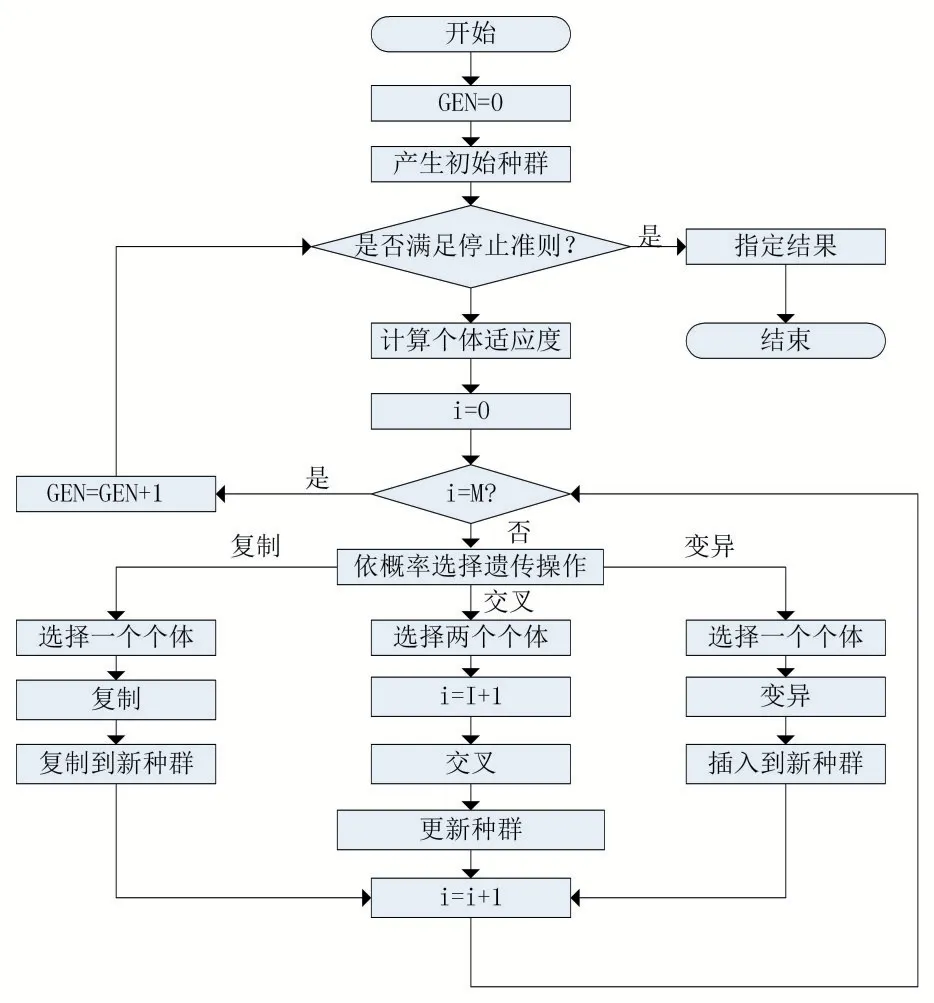
图1 遗传算法流程图
(1)部分映射交叉算子:部分映射交叉(Partial-Mapped Crossover,PMX)是由Goldberg 与Lingle 提出的[12]。在父母身上选择两个随机切割点来构建后代后,切割点之间的部分、父母一方的字符串被映射到另一方的字符串上,剩余的信息被交换。例如,考虑两个双亲旅行,在第3 位和第4 位之间随机有一个切割点,在第6 位和第7 位之间有另一个切割点,如下所示(用“|”标记的两个切割点):

映射部分位于切割点之间。在这个例子中,映射系统是4↔5、5↔4 和6↔3。现在,两个映射部分相互复制,以生成如下子代:
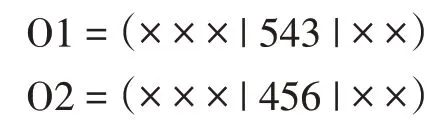
然后,我们可以(从原始父母那里)为那些没有冲突的基因直接进行填充表示,如下所示:
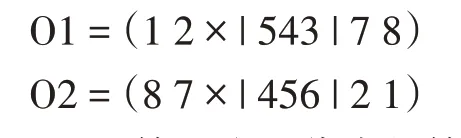
因此,第一个后代中的第一个×是3,它来自第一个亲本,但是3 已经在这个后代中,所以我们检查映射6↔3,由此得到:
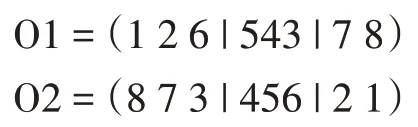
(2)顺序交叉算子。顺序交叉(Order Crossover,0X)是由Davis 提出的[13]。它通过选择父代的一个子代,并保留另一个父代的相对位序来建立后代。例如,考虑以下两个父母的旅行(随机地用“|”标记两个切割点):

后代是以下列方式产生的。首先,这些比特以类似的方式被复制到后代的切口之间,这就给出了
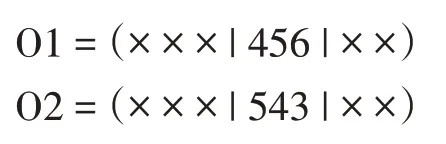
此后,从一个父代的第二个切割点开始,以相同的顺序复制另一个父代的位,省略现有的位。从第二个切割点开始,第二个父代中的位顺序为“2→1→8→7→6→5→4→3”删除第一个后代中的位4、5 和6 后,新序列为“2→1→8→7→3”该序列从第二个切割点开始放置在第一个后代中:
O1=(873|456|21)。类似地,我们也完成了第二个代:
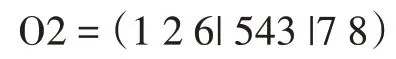
(3)循环交叉算子。循环交叉(Cycle Crossover,CX),首先由Oliver 等人提出[14]。使用这种技术来创造后代,使得每一个位置的基因都来自父母中的一方:
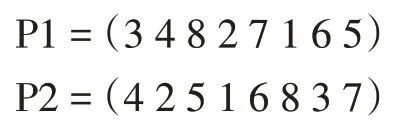
应用CX 技术后,产生的后代如下:
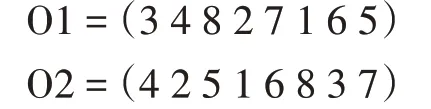
和他们的父母完全一样。子代与父代相同在遗传学中是不存在的,在算法中将会严重影响种群的丰富性,不利于算法的全局搜索能力。
2 改进循环交叉算子
本文基于循环交叉算子(CX)提出一种新的交叉算子自适应改进循环交叉算子(ICX),其工作原理与CX相似,与此同时,它使用循环直到最后一位从父母那里产生两个后代。并且本文提出的ICX 不再是从父代中随机的选择基因作为子代第一个基因,本文固定某个父代的第一个基因为本文最初选的基因,也就是说某个父代的第一个基因一定是位于其中一个子代基因序列中的第一位,其中关于具体父代的选择我通过判断父代适应度来确定,以适应度较大父代的第一个基因作为第一个子代的第一个基因。同时本文参考文献[15]采用了自适应交叉率。以下是其具体的交叉步骤:
第一步:在当前交叉率下选择双亲进行交叉操作;
第二步:计算父代适应度,将适应度较大父代中的一个基因为第一个后代的第一位(假设是第二个父代);
第三步:从步骤2 中选择的基因在第一父代中找到,并选择相同位置处第二个父代中的基因,再找到第一个父代中该基因的位置,最后,将为第二个父代该位置处的基因,作为第二子代中第一个位置处的基因;
第四步:从步骤3 中选择的基因在第一个父代中找到,并选择相同位置处第二个父代中的基因,作为第一个子代中第二个位置处的基因。(注意:对于遗传给第一个后代的基因,本文选择两次移动,对于遗传给第二个后代的基因,选择一次移动);
第五步:往后的每个位置重复步骤3 和4,直到第一个父代的第一位不再出现在第二个子代中(完成一个周期),过程可能终止;
第六步:如果留下一些基因,并将已经遗传的基因在其两个父代中的位置省略。对于剩余的位,重复步骤2、3 和4 以完成该过程。
第七步:比较两个子代个体的适应度,对于适应度较小的子代进行剔除,更新交叉率。
在文献[16]中提出了一种交叉算子CX2,也是解决了循环交叉算子种会产生与父代相同子代的情况,但是没有对父代中基因的选择做出规定,而是随机选择一个父代,同时该文献中的交叉率为固定值。
3 性能测试
为了体现出本文所提出算法相比于经典交叉孙子和对比交叉算子CX2 的优越性,其中算法参数的选择保持和对比CX2 算子试验中相同的参数。
(1)实验一:为了证明算法的一般性,本文选择TSPLIB(包含了TSP 及其相关问题的问题库)中的3 个实例Gr21、Fri26 和Dantzig42 如表1。三者均是对称旅行商实例且城市节点数量不多。
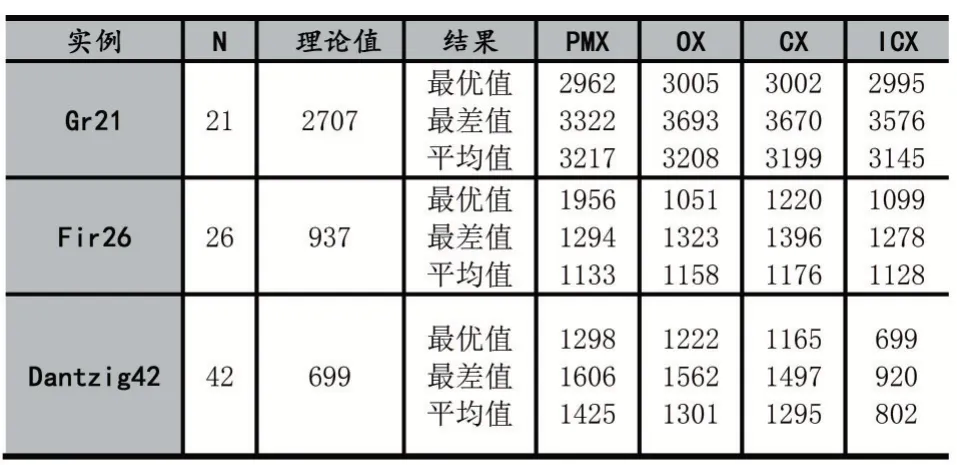
表1
(2)实验二:为了验证本文算法在非对称性旅行商问题和大规模旅行商问题中的表现,选择TSPLIB 中7个 非 对 称 的 旅 行 商 实 例ftv33、ftv38、ft53、ftv170、rbg323、rbg358、kro124p。对于每个实例,保持实验运行次数。前三个实例中为算法选择公共参数,即种群大小M、最大遗传代数G、初始交叉Pc 和突变Pm 概率相同,后四个实例中将种群大小M、最大遗传代数G相同。

表2
4 实验分析
实验一中,本研究选取了对称TSP 实例,结果显示ICX 相较于其他算子在收敛精度和稳定性上仍有提升。尤其在实例Dantzig42 上效果最为显著,并且ICX的最差值竟然比其他算子的最优值还有更加接近精确的最佳值。在最终的效果上,ICX 相比于PMX、OX、CX最优值分别提升了46%、43%、40%。ICX 与对比算法CX 在实验中达到过精确的最佳值699,而PMX、OX、CX 却没有给出过一次最佳值。同时相较于CX2 最差值和平均值本文提出的交叉算子ICX 明显更优。
实验二中,本研究选用了非对称TSP 实例,其城市节点数量从34 到358,其中Ftv33、Ftv38、Ftv53 在种群大小和最大遗传代数上区别于后面四个实例。实例Ftv53、Ftv170 中,ICX 在最终效果上的提升最为明显。相比其他三种经典交叉算子,ICX 在这两个实例中最优值的提升分别为:18%、21%、20%;52%、58%、50%,相比于对比交叉算子CX2 可以看到越是在城市节点数量较多的实例中如,Rbg323、Rbg358、Kro124p 提升最为明显。值得注意的是,在实例Rbg323 中ICX 的最优值反而是略低于OX,平均值低于PMX、OX,而ICX 算子有明显的改善。同样在实例Kro124p 中对比算子CX2 的表现是不及PMX 的,但本文提出的交叉算子变现是几种交叉算子中最好的。
5 结语
根据上述对比实验总结出,本文所提出的改进循环交叉算子ICX,在绝大数情况下相比于PMX、OX、CX有着一定的提升,具有一定的适用性。总体来说在遗传算法中使用本文所提出的交叉算子ICX 在大多方面比使用经典交叉算子PMX、OX 和CX 交叉算子表现得更好,在针对ft53、dantzig42 和ftv170 实例时,算法效率分别超过20%、70%和100%,同时相较于CX2 本文提出的算法有着更好的泛化性能。总结得出,本文提出的改进循环交叉算子确实有助于遗传算法收敛精度的提升,尤其是在城市节点较多的实例中,本文提出的交叉算子ICX 比CX2 有更加优异的表现。

