把握新教材，培养学生的实践能力和创新意识

温惠江

摘  要：常言说得好，有改革才有发展。社会在飞速发展，我们的课程改革早已迫在眉睫。从去年开始，我校开始试用华东版的新教材，经过一年的实践，我认为：要想出成绩，就一定得把握教材，培养学生的实践能力和创新意识。

关键词：把握;培养;实践能力;创新意识

新一轮的课程改革，对广大教育工作者来说，必须转变教学观念：突出“鼓励学生自主探索与合作交流”这一重要的学习方式。我经过一年的摸索，课堂教学发生了可喜的变化：学生思维活跃，敢于质疑，乐于表现自已，师生配合默契，收到了较好的教学效果。下面谈谈我的具体做法。

一、重视培养学生的应用意识和实践能力

1、让学生从现实的生活和知识经验中学习数学和理解数学。

教育学和心理学的研究表明：当学习的材料与学生已有的知识和生活经验相联系时，学生对学习才会感兴趣。

在教授《列代数式》一课时，我做了一个对比。以前按照传统的教学方法，先是在堂上罗列出学生以前学过的许多数学公式，给出代数式的定义及有关概念的说明，然后就是讲例题、做练习，一节课下来，课堂气氛沉闷，效果也不理想。而现在根据新教材的素材大部分来源于学生的现实生活的特点，课堂一开始就引入一个实际的问题情境（七年级（上）P86）：为了测试一种皮球的弹跳高度与下落高度之间的关系，通过试验，得到下列一组数据（单位：厘米）

在这个问题中，如果我们用b（厘米）表示下落高度，那么相对应的弹跳高度为___________。学生看到这问题就来劲了，纷纷发表见解，讨论热烈，概括出表示弹跳高度的一个式子 b，反映出这种皮球弹跳高度和下落高度之间的数量关系。我借此机会列举了几个有共同特征的典型实例，让学生思考、互相交流。学生在交流中了解了“代数式”的含义，知道了为什么要学代数式，对这节课反应热烈，兴趣很大，收到了很好的课堂效果。

另外，新教材很多章节编排了实践与探索，使学生从所熟悉的现实情境和已有的知识经验出发，动手参与，在认识数学的同时，还能学到解决问题的策略。比如（七年级（下）P14）问题1：

用一根长60厘米的铁线围成一个长方形。

（1）使长方形的宽是长的 ，求这个长方形的长和宽。

（2）使长方形的宽比长少4厘米，求这个长方形的面积。

（3）比较（1）、（2）所得两个长方形面积的大小。还能围出面积更大的长方形吗？

让学生运用所学的知识进行运算、讨论、探索。通过探索学生发现，长方形在周长一定的情况下，它的长和宽越接近，面积就越大，当长和宽相等，即成为正方形时，面积最大。这一结论我们在日常生活中经常应用它，新教材在这方面很好地调动了同学的学习积极性。

调查情况表明，在一年的新教材教学实践中，学生对学习数学的兴趣明显提高（由开学初的45%上升至现在的75%）。

2、培养学生应用数学意识解决实际问题的能力。

为了使学生经历应用数学的过程，在新教材的使用中，我采取“问题情境--建立模型--解释、应用与拓展”的过程，从而提高解决问题的能力。

比如：（七年级（下）P35）问题1：“要用20张白卡纸做包装盒，每张白卡纸可以做盒身2个，或者做盒盖3个。如果一个盒身和2个底盖可以做成一个包装盒，那么能否把这些白卡纸分成两部分，一部分做盒身，一部分做底盖，使做成的盒身和盒底盖正好配套？”这一问题，从学生感兴趣的折纸活动开始，使学生知道包装盒的结构，通过操作、抽象分析和交流，通过数量之间的相等关系，建立数学模型（即方程或方程组），按要求设计分法：如果不允许剪开白卡纸，能否找到符合题意的分法？如果允许剪开白卡纸，怎样才能既符合题意又能充分利用这些材料？通过交流与验证等活动，获得问题的解，并對求解过程作出反思。在这个过程中，学生体会到“包装盒的结构与合成”、“把实际问题转化为数学问题”、“方程或方程组”等方面知识的联系与综合应用。

另外，新教材要求教学过程中要注重数学与其它学科的联系，增强学生应用数学的意识。我在平时的课堂设计中，突出数学应用的广泛性。如七年级数学课本（华东版·上）P8练习，涉及到经济学中成本与利率，讲到这一问题时，先让学生进行社会调查，到银行了解定期储蓄年利率情况，了解利息的计算;又如（七年级（上）P13）有奖销售活动问题等，这都与我们生活息息相关，学生能把所学的知识加以运用，既增强了学习兴趣，又提高了解决问题的能力。新教材还将计算器、电脑和网络等带入数学课堂，使数学学习潜力无穷，数学课堂充满生机，这又是新教材的独到之处。

二、重视引导学生自主探索，培养学生的创新精神

在教学活动中，学生是学习的主体，必须改变“教师讲、学生听”;“教师问、学生答”以及大量演练习题的数学教学模式。教师在教学中应多设计探索性和开放性的问题，给学生提供自主探索的机会。我在课堂教学的实践中，主要从以下两点进行：

1、引导学生动手实践、自主探索和合作交流。

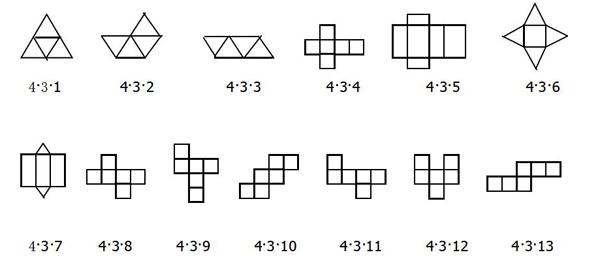
数学教学应注重引导学生动手实践、自主探索和合作交流。比如：在讲解立体图形的展开图时，在课堂上把课本P135---P137中图4·3·1-----4·3·13的十三个图分成四组，

分别让四个学习小组的同学用纸复制下来，用剪刀把它们剪下来，然后折一下，看看到底是什么图形。这样一来，学生的学习热情高涨，连班内数学基础较差的也不例外，学生在动手实践中寻找问题的答案，再让四个学习小组互相交流，很快就得出同一个立体图形，按不同的方式展开得到的平面展开图是不一样的，通过学生动手实践、自主探索，这一节课学生掌握得非常好。在每次考试中，这种题型得分率都很高。在新教材的教学中，让学生动手实践，是课堂教学的一个重要组成部分。

2、让学生在探索中进行归纳推理，发现规律。

合情推理能力的培养有助于發展学生的创新精神。新教材比较注重培养学生的推理能力，在课堂教学中应该给学生提供探索交流的空间，组织、引导学生“通过观察、实验、推理、归纳等数学活动过程”。例如课本（上）P181C组21题：我们知道，2条直线相交只有1个交点，3条直线两两相交最多能有3个交点，4条直线两两相交最多能有6个交点，5条直线两两相交最多能有10个交点，6条直线两两相交最多能有15个交点，……n条直线呢？这是一个明显的探索推理题，要求学生在探索中发现规律：每条直线都与其余的n-1条直线有一个交点，因此有n（n-1）个交点，但每个交点都重复了一次，所以n条直线两两相交最多能有 条直线。探索性的问题课本、练习题中经常出现，我们在平时的课堂教学中应引起重视。

又如，在学习了《有理数加、减法》的知识后，再组织学生处理课本（上）P10试试看这一内容，该题目要求学生在如图1所示的方格中，填入1，2，3，4，5，6，7，8，9这9个数，使每行、每列及对角线上各数的和都为15。学生对这题目的兴趣很大，但不知该从何处入手，我及时进行引导，应该先在哪一个格中填数？填什么数？这样一提示，班内一位思维较敏捷的学生很快举手回答：中间的一个数应填5，这时，课堂气氛“活”了起来，学生纷纷举手回答：1和9，2和8，3和7，4和6应分别与5在同一行，或同一列，或同一对角线上，因此，很快就有了问题的答案（如图2）。

就此题目进行猜想，我在黑板上给出四组数，分别为：① 3，4，5，6，7，8，9，10，11    ② -10，-9，-8，-7，-6，-5，-4，-3，-2  ③  0，2，4，6，8，10，12，14，16    ④  -4，-2，0，2，4，6，8，10，12   让四个学习小组讨论、试填，能否使每行、每列及对角线上各数的和相等呢？这时学生的学习劲头可大了。经过四个小组学生激烈讨论，四组数都能做到，比如第④组，答案如图3，只不过每行、每列及对角线上各数的和不再是15，而变成了12。

看起来问题已经解决了，这时，一学生举手提问：究竟怎样的9个数才有这规律呢，填写时能否有规可循？这下气氛可“热闹”了，有的说任意9个数;有的说连续的9个整数;有的说不能确定等等。经过大家探索、总结，可得出以下规律：把9个数按小到大排列，凡符合等差数列（可向学生解释这样的规律即可）都可以，这时，一位学生举手发言：我认为可以把这个方格图看作一个人，左、右上角为肩，左、右下角为足。填写规律如下：把符合规律的9个数由小到大顺序排列，分别标号为1至9。按口决：“二四为肩，六八为足，左七右三，戴九履一，五居中央。”同学们听了这位学生的回答，纷纷动手验证这一规律，实践证明，这一规律的确可行，这样不但总结了这一问题的规律，还能使学生进一步认识归纳推理。实践证明，学生对这问题掌握得非常好，每次测试的答对率都接近100%。

经过一年的实践，我所教的两个班，学生实践能力和创新意识得到了较好的培养，收到了较好的教学效果。在全市自查考试中两班的数学平均分为68.4分，比市平均分62.8分高出5.6分。我相信，在今后的教学改革过程中，充分把握新教材，培养学生的实践能力和创新意识，不断探索、总结，一定能收到更好的教学效果。

参考文献

[1]  唐渭明.解读《数学课程标准》实施研究性学习的策略[J].中学数学杂志，2003（12）：10-11.

[2]  陈京山.对《数学课程标准》的一种解读[J].教学与管理，2002（34）：48-50.