基于网格运动约束的遥感图像配准算法
李 丹,徐倩南
(安徽工业大学 电气与信息工程学院,安徽 马鞍山 243032)
0 引 言
遥感图像的配准常用来获取更加全面的地理信息,正确辨识相关的地理位置等。基于特征的图像匹配由于其稳健高效的特点成为研究的热点[1]。经典的SIFT(scale-invariant feature transform)[2]和SURF(speed up robust feature)[3]算法由于使用高斯金字塔构建尺度空间,高斯模糊导致对象边界信息的丢失,影响了定位的准确性。KAZE[4]算法通过AOS(additive operator splitting)数值逼近方法建立非线性尺度空间,计算量较大,实时性难以满足[5]。AKAZE[6]中,作者引入快速显示扩散数学框架FED(fast explicit diffusion)来求解偏微分方程,比当下其它的非线性模式建立尺度空间都要快,同时比KAZE中的AOS[7]更加准确。ORB(oriented FAST and rotated BRIEF)[8]算法结合FAST与BRIEF(binary robust independent elementary features)[9]提高了计算速度,但缺少尺度不变性。BRISK(binary robust invariant scalable keypoints)[10]利用像素灰度值的比较来构建二进制描述子,速度较快且具备旋转与尺度不变性,但是匹配鲁棒性较差[11]。GMS(grid-based motion statistics)[12]基于网格的运动估计方法,通过在粗匹配点相邻的区域中统计具有匹配关系的特征点数量来进行匹配,快速且鲁棒性强[13]。为了保证特征点定位的精度,本文采用AKAZE(accelerated-KAZE)算法来检测特征点,同时为了算法的实时性,使用速度较快且具有尺度与旋转不变性的二进制描述子BRISK进行特征描述,为了提升匹配的鲁棒性,我们采用基于网格的运动估计方法对描述子进行匹配,最后利用随机采样一致性算法剔除错误的匹配点。
1 算法主要原理
基于网格运动约束的遥感图像配准方法流程如图1所示。

图1 算法流程
1.1 AKAZE特征点检测
AKAZE特征点检测首先是构造非线性尺度空间,通过非线性扩散滤波方程,即流动函数的散度来表示图像亮度在不同尺度空间变化的方法。利用如式(1)所示的非线性微分方程来描述
(1)
其中,L代表的是图像亮度,c(x,y,t) 是传导函数,t表示尺度参数。非线性尺度空间由O组图像组成,每一组包括S层,其中每组每层的尺度参数是σi(o,s),σi的单位是像素而ti的单位是时间,因此需要将两者进行转换。对原始输入图像进行高斯滤波,滤波后的图像梯度直方图70%位置上的值作为控制因子。获取输入图像与控制因子之后,采用FED算法对扩散方程进行求解来构建非线性尺度空间[7]。
尺度空间构建完成后,然后采用Hessian矩阵进行特征点提取,如式(2)所示
(2)
其中,Lxx,Lyy,Lxy为L的二阶微分,σi为尺度归一化因子,每一个像素点分别在当前及其上下两层以3*3窗口进行极值点搜索,得到的极值点为初步关键点,还要利用泰勒公式进行亚像素点的精确定位,最终定位的点即为特征点。
1.2 Brisk特征描述
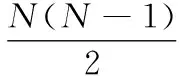
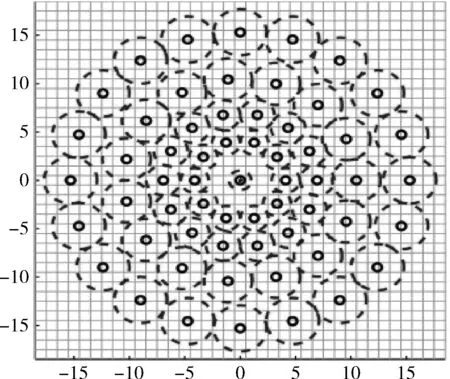
图2 BRISK描述子采样模式
以关键点为中心将采样点旋转α角度,考虑其中短距离点对子集中的512个点对,进行二进制编码,编码方式如式(3)所示
(3)

1.3 GMS匹配
为了解决当前特征匹配存在的匹配速度和匹配效果难以同时满足的问题,本文采用基于网格运动估计的方法来进行特征点的匹配。该方法的核心思想是运动的平滑性导致了正确匹配的特征点邻域有较多匹配的点,相反错误的匹配点对由于对应着三维空间中不同的位置,匹配对邻域内支持的点数较少,因此只要通过计数邻域的匹配点个数就可以判断一个匹配点对正确与否[12]。
首先利用暴力匹配获取两张图像的特征匹配点对集合,GMS算法通过分析匹配点对邻域内支持匹配点对的数量,来分离匹配点对集合中的正确和错误的匹配。假设匹配对xi在两幅图中分别对应的邻域为{a,b},χi表示在邻域 {a,b} 内的特征匹配对的数量,那么xi的支持匹配点对数量Si为
Si=|χi|-1
(4)
在特征点匹配中,每一个特征点的匹配是独立的,因此匹配对xi所对应的邻域内的其它n个匹配对服从二项分布,如式(5)所示
(5)
Si表示当前特征点邻域a内的n个点匹配到两幅图像对应的相同物体区域b的次数,pt表示邻域 {a,b} 对应同一个三维位置时,区域a内的特征点的匹配点在区域b内的概率,pf表示邻域 {a,b} 对应的是不同的三维位置时,区域a内特征点的匹配点在区域b内的概率。
为了提高S分数区分正确-错误匹配的能力,采用多邻域模型来代替原先的单邻域模型,那么支持匹配点对数量Si的计算如式(6)所示
(6)
那么Si的分布扩展为式(7)形式
(7)
其中,n表示每一个小邻域内的平均的特征点数,K表示小邻域的个数。Si分布的均值和标准差分别为
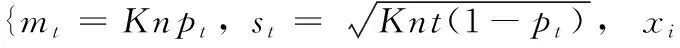
(8)
如图3所示,正确的匹配和错误的匹配都有自己的分布,且均满足二项分布,为了使它们的区分度更大,首先这两个分布要相隔足够远,即mt-mf足够大,其次这两个分布的标准差或方差要足够小,区分能力得分如式(9) 所示

(9)
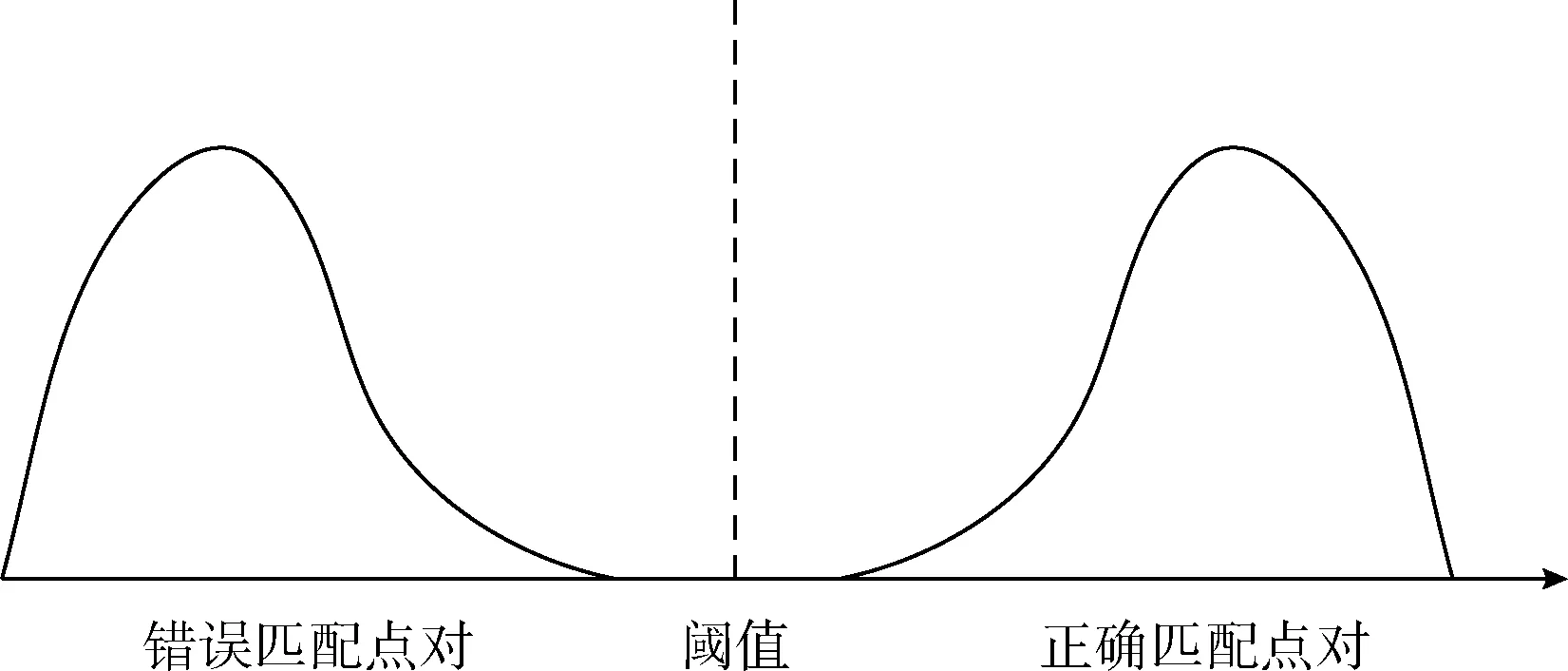
图3 Si分布
GMS算法将一幅图分成N×N的不重叠的网格,并且选取3*3网格作为一组来计算Si的值。为了获得足够大的区分能力得分P, 经过实验选取的较为合理的参数为K=9,n=25,N=20。 当支持匹配点对数量Si大于一定阈值的时候,便认为是正确匹配。阈值τ的计算如式(10)所示
τ=mf+αsf
(10)
其中,α是调节参数,mf的值通常很小,α的值很大,所以式(10)又可以近似表示为
τ≈αsf
(11)
2 实验数据分析
对于本文提出的基于网格约束的遥感图像匹配方法,我们进行了大量的实验,本实验运行环境是Intel core5的CPU,64位Windows 10操作系统,所有算法集成在Visual studio和OpenCV3.1环境下实现。为了验证算法效果,选出如图4所示的图(a)~图(c)这3组IKONOS卫星遥感图片进行对比,图(a)组表示的是图片的尺度变换,图(b)组对应的是图片的亮度变换,图(c)组是图片的旋转变换。通过3组图片,分别对本文算法的抗尺度变化,抗亮度变化以及抗旋转变化性能来进行验证。将本文算法与AKAZE算法,KAZE算法以及速度较快的ORB算法进行对比,从匹配结果图,特征匹配速度,特征匹配正确率3个方面来对每个算法进行定量的评价。

图4 实验数据遥感
图5显示的是4种算法对3组遥感图像的匹配结果图,本文算法通过RANSAC算法剔除误匹配点,其余3种算法特征点匹配均采用暴力匹配算法,且均通过RANSAC算法对匹配点进行提纯。其中图(a)组是尺度压缩变换下匹配结果图,图(b)组是亮度变换下匹配结果图,图(c)组是旋转变换下匹配结果图。从最直观的角度我们可以看出,在图(a)组匹配图中,由于尺度压缩分辨率较低,4种算法匹配图都有明显的误匹配,其中KAZE算法错误率最高,AKAZE和ORB算法错误率较少,本文算法匹配效果相对最稳定。图(b)和图(c)在4种算法下都取得较好的匹配效果,但是可以明显看出文中算法匹配效果突出,这也进一步证实本文算法在尺度变化,光照变化,旋转变化下都有较好的鲁棒性。

图5 配准结果比较
采用对比匹配时间长短的方法来评价4种算法特征匹配的速度,匹配时间越短,特征匹配速度越快。表1给出了分别使用AKAZE算法,ORB算法,KAZE算法和本文算法对图4所示的图像数据进行特征匹配所用的时间,其中AKAZE,KAZE和ORB算法均采用暴力匹配进行粗匹配,然后利用随机采样一致性算法进行提纯,为了更鲜明地比较出各个算法匹配的快慢,图6给出了各种算法匹配时间的折线图。

表1 特征匹配用时比较/s
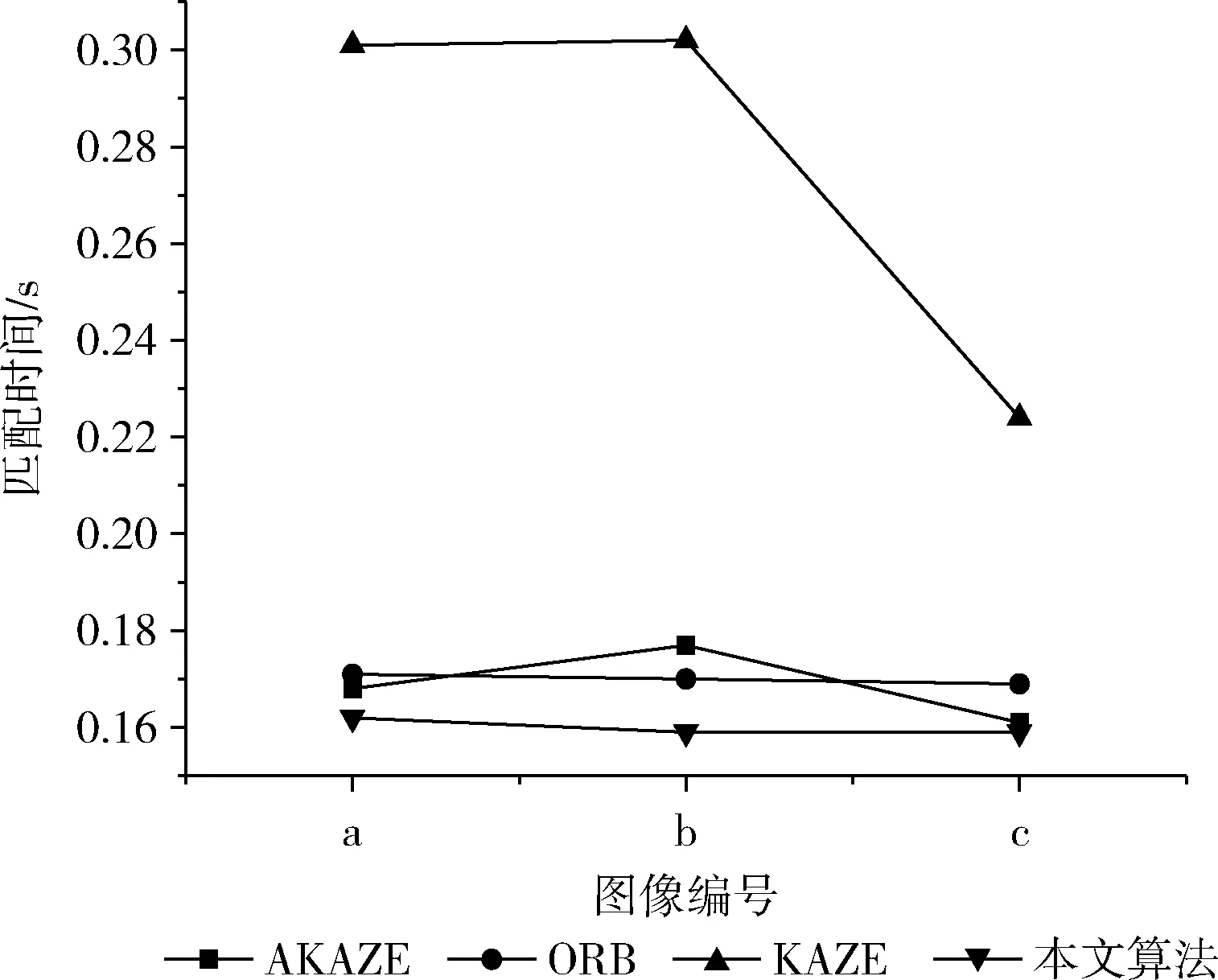
图6 配准时间比较
由折线图可以很明显看出,在匹配用时上,KAZE算法匹配用时最多,速度最慢,本文算法匹配用时最短,速度最快,ORB算法和AKAZE算法用时相近,由此可得,本文算法在匹配时间上效果较好。
匹配正确率CMR的定义是匹配正确点对数与总的匹配点对数之比,CMR是一种客观的评价指标,匹配正确率越高,匹配性能越好。图7所示的是4种算法对3组遥感图片进行匹配的正确率效果图,柱状图从左到右的顺序分别是AKAZE算法,ORB算法,本文算法,KAZE算法。从图7中可以看出,本文算法在3组图片下的匹配正确率相较其它3种算法皆为最高,这表明本文算法在尺度变化,亮度变化以及旋转变化下皆有不错的匹配性能,其中在抗尺度变化下匹配性能最为突出,AKAZE和KAZE算法匹配效果次之,ORB算法匹配效果较差,这也进一步验证了本文算法具有较稳定的匹配性能。
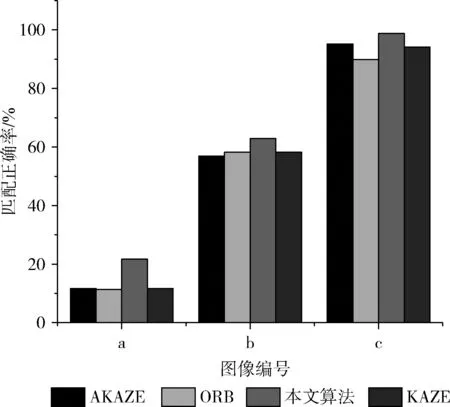
图7 匹配正确率比较
3 结束语
本文提出了一种基于网格运动约束的遥感图像的局部特征匹配方法,该方法首先利用AKAZE算法进行特征点提取,采用二进制描述子BRISK对检测的特征点进行描述,然后使用GMS基于网格的运动估计方法对特征点进行精确匹配,最后使用RANSAC算法对匹配的点对进一步提纯,剔除误匹配点。实验中将本文算法与鲁棒性较强的AKAZE算法,KAZE算法和速度较快的ORB算法从匹配效果图,匹配时间,匹配正确率3个方面进行比较,实验结果表明,本文算法在提高特征匹配速度的基础上保证了特征匹配正确率,在处理旋转变化较大的图片时依然能保持相对较好的匹配效果。由此可得,本文算法适合用于遥感图片匹配处理。

