基于时间序列的多维距离聚类异常检测方法
丁建立,黄天镜,徐俊洁,王 静
(中国民航大学 计算机科学与技术学院,天津 300300)
0 引 言
在GPS定位、目标探测技术快速发展的时代,为了保障飞机飞行安全,需要存储和分析大量的飞行相关的时空轨迹数据。民航飞行时空轨迹数据包含了经纬度坐标、记录时间、飞行高度、飞行速度、航向等多种属性[1]。在实际飞行中,民用飞机一般按照标准飞行程序,依靠地面空中交通管制人员的指挥来调配飞行[2],但特殊情况会出现实际航迹偏离标准程序的情况,通过对轨迹数据的检测可以发现偏离正常飞行模式的轨迹[3],保障飞行安全。
已有的轨迹异常检测算法主要分为以下4类:基于统计的方法、基于距离的方法、基于密度的方法和基于聚类的方法[4,5]。以上方法并没有充分利用轨迹的类型、位置、速度和方向等多维特征,而传统的聚类的方法主要采用距离作为相似度的评价指标,认为两个对象的距离越近,其相似度就越大,忽略了飞行轨迹的数据点的有序性以及数据点本身具有的航向、速度等特征,不能有效挖掘飞行轨迹中的异常行为。
本文针对传统聚类异常轨迹检测方法中存在的局限性,使用广播式自动相关监视(automatic dependent surveillance-broadcast,ADS-B),提出了基于时间序列的多维距离聚类异常检测方法。利用改进Hausdorff距离计算不同轨迹数据之间的相似距离,并结合层次聚类算法检测异常飞行轨迹。相比只采用轨迹位置的Hausdorff距离函数进行异常检测方法,改进方法能够更全面地对轨迹数据进行分析,找到轨迹数据在位置、速度、方向等特征上的异常,提高飞行轨迹数据的异常行为检测的精确性。
1 相关概念描述
1.1 轨迹数据
轨迹数据是由一系列随时间变化的时空数据点组成,即TR={P1,P2,…Pi,…,Pn}。 ADS-B系统可以自动地从相关机载设备获取参数向其它飞机或地面站广播飞机的位置、高度、速度、航向等信息[5],针对于ADS-B数据来说,这里第i个数据点可以表示为Pi=(loni,lati,vi,θi,ti),loni,lati为数据点的经度和纬度值,vi为数据点的速度,θi为数据点的航向,ti为该数据点的时间戳信息。
轨迹集合可以表示为n条轨迹数据的集合,即T={TR1,TR2,…,TRi,…,TRn}, 其中TRi表示第i条轨迹数据。
1.2 轨迹相似度
正常情况下某段航线的飞行轨迹是相似的,但不排除某些突发情况,如躲避物体或检测数据丢失等情况,这些情况会导致轨迹数据发生异常,使得该飞行轨迹偏离正常轨迹,严重时可能导致轨迹相似度发生较大差异。仅考虑位置特征的轨迹异常检测算法会忽略掉时间、速度和方向等运动状态对飞行轨迹数据的影响,不能有效挖掘历史数据[6],使得正常的轨迹行为被检测为异常轨迹,或者真正的异常的轨迹行为不能准备被发现。
(1)时间因素对轨迹相似度的影响
飞机飞行的轨迹是随时间而逐渐变化的,在已有轨迹异常检测算法计算轨迹相似度时,仅考虑了轨迹的位置信息,没有考虑时间因素对飞行轨迹的影响,导致检测效果较差。例如在计算如图1所示的4条轨迹的相似度时,如果仅考虑位置信息,很有可能得到4条轨迹相似度归属于相同的类,显然得到的结果不能完全体现出轨迹的运动规律。图1中4条轨迹的前期运动形态趋势相似,但轨迹Tr3和Tr4随着时间的变化后期的运动趋势同Tr1和Tr2出现了较大的差异。在考虑时间特征情况下,就可以将Tr3和Tr4轨迹同Tr1和Tr2进行区分。
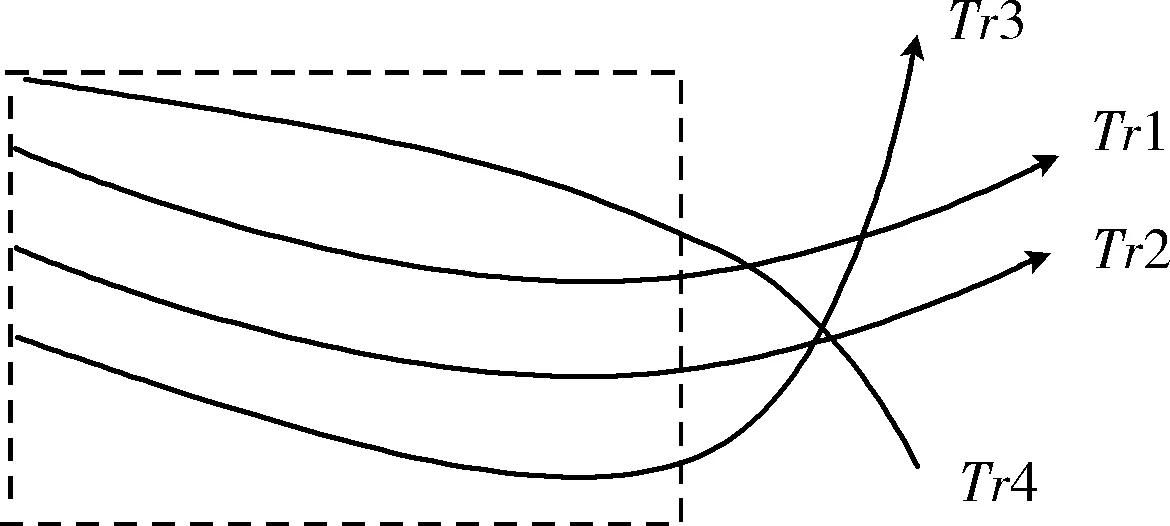
图1 相似轨迹
(2)速度和方向因素对轨迹相似度的影响
为了更好地进行轨迹异常检测,在考虑位置特征,时间特征的基础上,引入轨迹本身具有的速度,方向等运动特征。如图2所示,显而易见,通过平移转换图中3条轨迹可以重叠,如果不考虑速度和方向的特征,在计算相似性时会判断为3条轨迹是相似的。但是在考虑到速度和方向特征前提下,明显Tr1、Tr2、Tr3轨迹两两均不相同。Tr2与Tr1速度相同却方向不同;Tr3与Tr1方向相同却速度不同,速度要比Tr1快[7]。
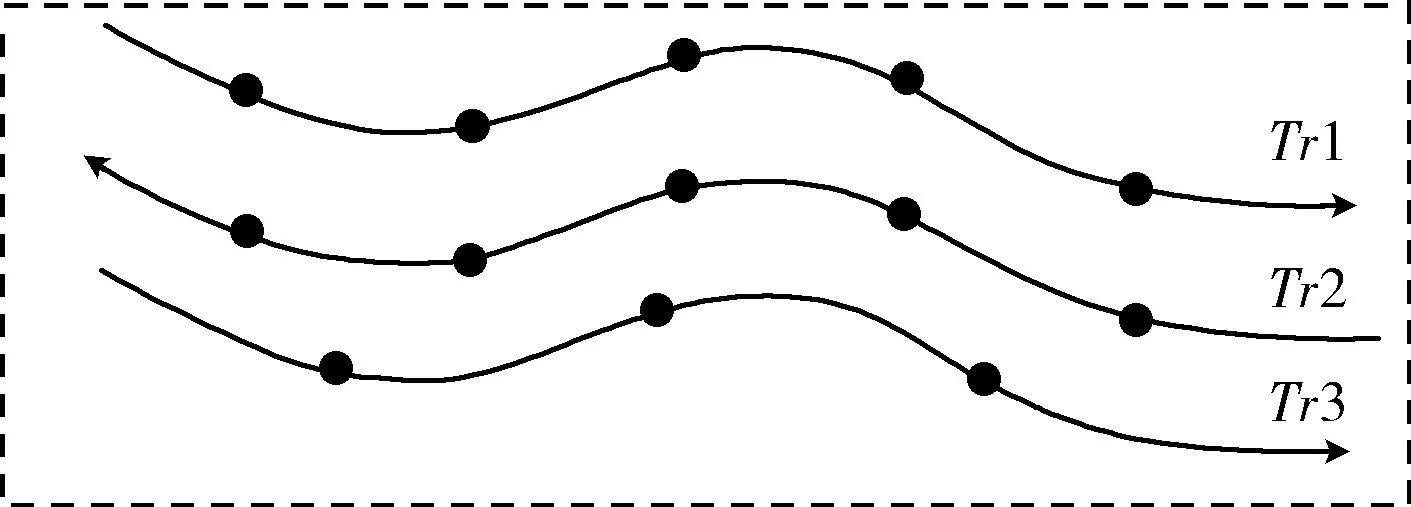
图2 运动轨迹
针对上述问题,本文在利用Hausdorff距离计算轨迹相似性时,在时间特征的基础上结合了轨迹的速度、方向、位置等多重特征[8,9],利用基于时间序列的多维特征对Hausdorff距离函数进行改进,提高了轨迹数据相似性计算的精确性,进一步提高轨迹异常检测的效果。
2 基于多维距离的层次聚类算法
2.1 算法描述
本文提出的基于多维距离的层次聚类算法由两部分组成:基于时间序列的多维Hausdorff距离算法和多维Hausdorff距离的层次聚类算法。基于时间序列的多维Hausdorff距离算法首先将方向、速度、位置多维特征融入Hausdorff距离公式中,通过构造的多维Hausdorff距离计算航迹数据集中任意航迹的相似距离[10],构造出航迹间相似性矩阵。多维Hausdorff距离的层次聚类算法基于该相似性矩阵进行层次聚类,生成具有层次结构的聚类图。由于异常与正常航迹之间的相似度值差异较大,可以通过聚类结果较为直观的将异常航迹与正常航迹分类,从而发现异常航迹。
层次聚类(hierarchical clustering)是一种基于原型的聚类算法,试图在不同层次对航迹数据集进行划分,从而形成树形的聚类结构,同时它不需要事先指定簇的数量[11]。
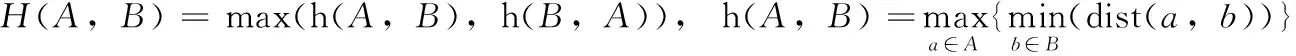
2.2 基于时间序列的多维Hausdorff距离算法
已有的计算Hausdorff距离算法中仅使用了轨迹数据的位置特征,而实际目标轨迹的时间特征和速度、方向等运动特征都是描述轨迹的重要信息,本文提出的基于时间序列的多维Hausdorff距离算法把轨迹数据看作是按照时间序列由有序的数据点组成的。假设轨迹TrA={a1,a2,…,ai,…,an} 和轨迹TrB={b1,b2,…,bi,…,bm}, 其中n,m≥3,ai、bi分别为TrA、TrB在第i时刻的数据点。本算法在考虑时间序列的基础上,引入位置、速度、方向等特征来计算多维Hausdorff距离,即基于时间序列的多特征两点距离(time series multi-feature distance,TMFD):具体如下所述:
(1)位置特征
posdis(ai,bi)=dist(ai,(bi,bi-1,bi+1)) 表示两条轨迹上的两点的经纬度距离,本文采用Haversine公式计算。其中,轨迹A中任意点ai仅与轨迹B中相对应点bi以及前后相邻两点比较。
(2)速度特征
spedis(ai,bi)=dist(Vai,(Vbi,Vbi-1,Vbi+1)) 表示两条轨迹上两点之间的速度欧式距离,点的速度分解为垂直速度v*sinθ、 水平速度v*cosθ。
(3)方向特征
angdis(ai,bi)=dist(θai,(θbi,θbi-1,θbi+1)) 表示两条轨迹在内部方向改变程度,反应了轨迹的波动状况,使用绝对值距离来表示。
即综合上述公式
(1)
TMFD(ai,bi)=ωp×posdis+ωv×spedis+ωθ×angdis
(2)
其中,ωp+ωv+ωθ=1, 且ωp≥0,ωv≥0,ωθ≥0分别表示位置特征、速度特征、方向特征的权重因子,可根据应用场景的不同,适当调整权重的选择。
该算法从3个方面体现出轨迹数据的时空运动特征对异常轨迹行为检测的优势:
(1)轨迹点的运行特征具有多维性。改进后函数表达式中不仅使用点的位置特征,将点的速度特征以及方向特征考虑进去,利用Hausdorff距离计算方法,提高复杂运动状态下轨迹相似度计算的准确性。
(2)轨迹点的运动是有序的。假设TrA中的第一个点a1与TrB中最后一点bn之间距离最大,则按照最初计算Hausdorff距离原则,则定义h(TrA,TrB)=dist(a1,bn)。 明显所选取点有一定的时间差,在计算相似度时误差过大。且轨迹TrA中任意点与TrB中所有点比较也不能体现出时间有序性特征。为了避免上述问题,令点ai、bi分别为TrA、TrB在同一时刻i的轨迹点,仅使用轨迹TrA中的每个点ai与轨迹TrB上的bi点与点bi前后相邻两点之间比较,减少计算量同时体现出轨迹的有序性。
(3)轨迹点的运动是连续性。选取点bi以及bi前后相邻两点进行比较,最大程度满足在时间排序上的一对一,由于轨迹前后相邻两点在速度及方向上变化不会过大,同时采用一对三保证了点与点之间的连续性,在计算轨迹相似度时提高准确率。
2.3 多维Hausdorff距离的层次聚类算法
对轨迹数据集使用基于时间序列的多维特征距离方法计算得到任意两条轨迹之间的多维相似距离h(TrA,TrB),进而构造出计算航迹间的相似性矩阵R,即
其中,rij表示第i条轨迹与第j条轨迹之间的相似距离。主对角线元素0表示轨迹自身与自身比较的相似距离。
表1为结合轨迹数据的多维Hausdorff距离的层次聚类算法。该算法的输入是轨迹数据集T,输出是聚类图。在多维Hausdorff距离的层次聚类算法中,步骤1使用基于时间序列的多维Hausdorff距离计算T中任意两条轨迹之间的相似距离;步骤2使用步骤1中的相似距离构造相似性度量矩阵R;步骤3根据n条轨迹数据构造n个类,每个类中只包含一条轨迹,并设置每一个类的平台高度均为0;步骤4采用自底向上的层次聚类算法合并相似距离最近的两类为一个新类(也就是选择矩阵R中rij的最小值,合并轨迹i和轨迹j对应的两个类为新类),并且以轨迹i和轨迹j的相似距离作为该新类在聚类图中的平台高度;步骤5计算新类与其它各类的相似距离,若当前类的总个数已经等于1,则输出聚类图,否则继续步骤4。

表1 多维Hausdorff距离的层次聚类算法
3 实验分析
3.1 实验数据集
本文采用的数据集是来自Flightradar24的ADS-B数据,该网站提供实时的航班信息数据。其中选择北京到上海的45天以及北京到杭州的20天的部分飞行航迹。实验场景根据位置、速度、航向特征的取值差异,按比例确定权重因子的大小,降低权值对构造的多维距离的层次聚类算法的影响。
为了更直观观察本文方法的聚类结果,图3(a)为根据本文所提出的聚类算法对北京至上海45条正常航迹以及北京至杭州20条的聚类结果,杭州与上海在地理位置上的航线差别不明显,能够有效验证方向及速度特征对聚类结果的影响。横坐标表示航迹数据集中的样本个数,坐标轴上的数字为对应的航迹编号,如图3(a)左侧聚类为 1~45 编号的航迹,表示北京至上海的45条航迹,右侧聚类为46~65编号的航迹,表示北京至杭州的20条航迹;纵坐标表示航迹间的相似距离。根据轨迹相似性距离值,同一航线的航迹属于同一聚类。如图所示,北京至上海为一个聚类、北京至杭州为一个聚类,符合实际情况。图3(b)为北京至上海航线的航迹聚类结果,图中聚类线没有较大落差,表示该航迹本身之间差距并不大,均在正常范围内(相似度值90)波动。

图3 航迹聚类
图4为北京至上海的航迹经纬度坐标的二维显示,横坐标表示纬度、纵坐标表示经度,所有的航迹并不是沿着一条直线,而是在一定范围内飞行。
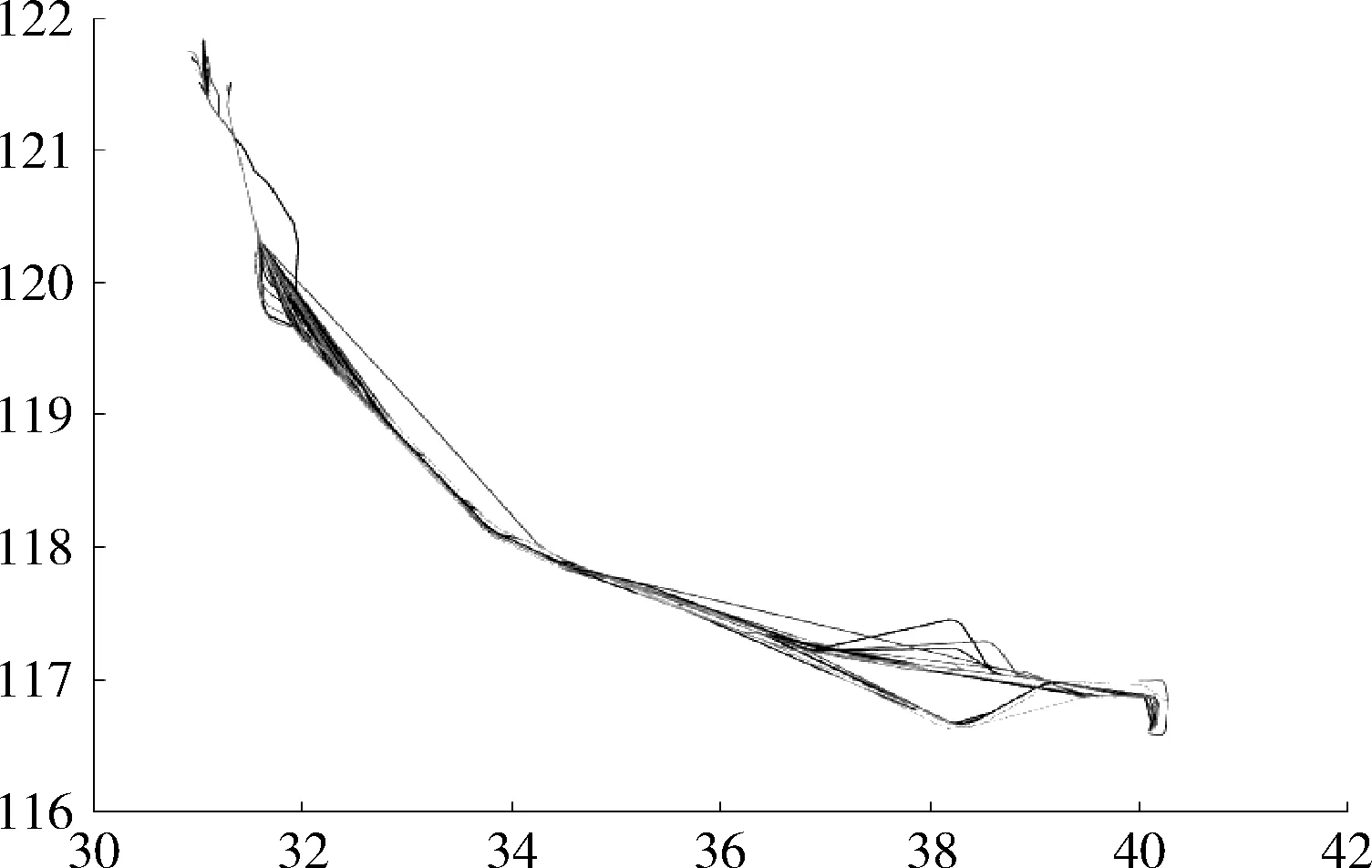
图4 北京到上海航迹二维图
3.2 实验评价标准
在进行异常检测时,针对于位置、速度、航向等特征分别随机选取北京至上海的5条航迹,修改航迹点使其偏离正常飞行航迹阈值,飞行速度为正常速度的1.5倍,修改航向为正常航向的相反方向。该实验结果通过计算正确率(Accuracy)、精确率(Precision)、召回率(Recall)、F1值(F1-score)来评价基于多维Hausdorff距离的层次聚类算法。以上评价指标计算公式

(3)

(4)

(5)
(6)
正确率定义为正确预测的正反样本数占所有样本的比例。精确率定义为预测是异常实际也是异常的样本数占预测是异常的样本数的比例。召回率定义为测试集中所有正样本样例中,被正确识别为正样本的比例。F1值是准确率和召回率的加权调和平均。其中,TP表示正样本被正确识别为正样本,TN表示负样本被正确识别为负样本,FP表示负样本被错误识别为正样本,FN表示正样本被错误识别为负样本。
3.3 实验结果
图5为在北京至上海的航迹中采用本文所述方法实验修改航迹速度、位置、航向的聚类结果。实验结果分析,聚类图中的横坐标表示航迹条数,坐标轴上的数字表示对应的航迹编号,纵坐标表示航迹之间的相似度值。图5(a)为对速度修改后的5条航迹与正常航迹的聚类结果,可以明显区别出修改后的异常航迹,通过本文提出多维Hausdorff距离的层次聚类算法,提高了轨迹相似度度量对速度变化的敏感度,使得修改速度后的轨迹与正常轨迹的相似度值相差较大,将正常与异常航迹聚为两类;图5(b)为对航向角度修改后的5条航迹与正常航迹的聚类结果,同样识别出异常航迹,将正常与异常航迹聚为两类。图5(c)为对轨迹点经纬度值修改的5条航迹与正常航迹的聚类结果,由图3(b)可看出,正常轨迹的相似度值最高在90左右,在修改航迹位置后,聚类图中异常航迹与正常航迹相比的相似度值约为120-130左右,远超出正常航迹聚类时的相似度,其中各别航迹区分不明显由于本身航迹并不是沿着一条固定线路不变,有一定的飞行范围,所以修改后的异常航迹的位置对正常航迹的聚类稍加影响,但不妨碍判断出异常的航迹,通过本文方法可以判断出异常轨迹。为了说明本文提出的算法的有效性,使用未改进的Hausdorff距离分别进行了与本文实验数据相同的5条位置异常航迹、5条速度异常航迹以及5条航向异常的航迹与正常航迹聚类的3组实验,计算异常航迹与正常航迹的相似度,由于原始Hausdorff距离在计算中仅考虑位置特征,所以对于修改位置的异常航迹可以用该方法判断出,但计算中并没有考虑速度和航向特征,所以在修改速度和航向的对比实验中并没有有效检测出速度和航向上的异常,表明本文方法在速度与航向上的检测提高了准确率。

图5 异常检测聚类
表2即原始Hausdorff距离算法与本文改进算法基于时间序列的多维距离聚类异常检测方法在相同修改条件下检测异常轨迹的对比结果。
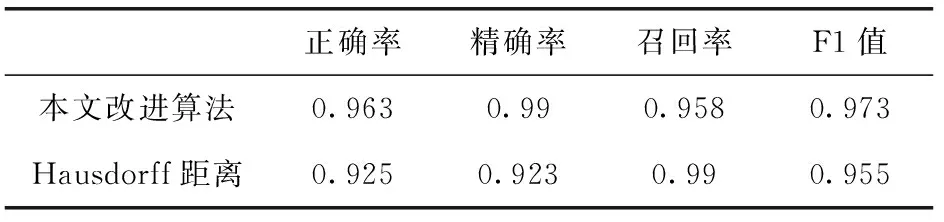
表2 与现有Hausdorff距离进行聚类对比
4 结束语
本文通过分析航迹数据的特征,针对现有的轨迹相似度度量方法存在的不足,提出了一种基于时间序列的多维Hausdorff距离,考虑轨迹本身的运动有序性以及轨迹点连续性特征的基础上,从位置、速度、航向这3个方面来计算轨迹的相似度,同时针对于“轨迹点有序”这一特征,使用一对三的比较方法减少了轨迹点之间的比较次数,降低了计算复杂度。采用ADS-B数据集,利用改进的多维Hausdorff距离进行层次聚类实验结果表明,该算法可以有效识别出异常航迹,验证了改进方法的有效性,对比实验结果表明,增加轨迹点的运动、方向特征提高了飞行轨迹数据的异常行为检测的精确性。在实际应用中,发现异常航迹对于查找民航飞机出现故障及漏洞有着重要的参考意义。

