PMLSM智能控制伺服系统的仿真研究

朱鹏涛，谭会生, ，肖望勇，张发明,

(湖南工业大学 a. 电气与信息工程学院；b. 交通工程学院；c. 理学院，湖南 株洲 412007)

永磁直线同步电机(permanent magnet linear synchronous motor, PMLSM)以其响应速度快、传递效率高、可控精度高和工作安全性能可靠等优点而被广泛地应用于高速度、高加速度和高精度的控制领域，成为近年来国内外的研究热点与前沿[1-6]﹒但PMLSM 具有功率因数低、非线性、时变不确定、结构复杂和边端效应等缺点，由于其时变性难以建立精准的PMLSM 数学模型，所以PMLSM 伺服系统想获得较好的控制性能较难实现[1-3]﹒模糊控制、神经网络和滑模控制等智能控制方法为开发高性能的PMLSM 伺服控制系统开辟了新的道路[1-2,4-6]﹒但是，模糊控制缺乏自适应性，神经网络控制算法存在训练样本过度拟合等问题，难以满足被控系统的实时性要求﹒为了克服采用单一模糊控制和神经网络等PMLSM 智能控制算法的不足，研究一种将模糊控制、神经网络、滑模控制和自适应学习结合在一起的PMLSM智能补偿滑模控制算法，以提高PMLSM 伺服控制系统的动态性能和鲁棒性﹒

1 PMLSM 伺服系统控制原理

PMLSM 伺服控制系统是集合了电流控制环、速度控制环和位移控制环的三闭环控制系统﹒首先，将给定位置信息与霍尔位置传感器采集到的 PMLSM 初级位置信息进行比较，并传送到位置控制器，形成位置闭环控制反馈；其次，将位置控制器变换得到的速度与位置信息经滤波求导得到的反馈速度进行比较，其差值送入速度控制器中，形成速度闭环反馈；进一步将位置传感器获得的位移数据通过相关算法形成坐标变换的电角度，且将速度控制器所得交轴电流输入电流控制器进行电流补偿，抑制推力波动；再将三相交流电经过坐标变换后与输入电流进行比较，其差值送入电流控制器，形成内环电流反馈；最后，将电流控制器输出的电流进行一系列坐标变换和计算，形成PWM 信号并控制逆变器后得到三相交流电流控制PMLSM[1]﹒PMLSM伺服系统的结构如图1 所示﹒

图1 PMLSM 伺服系统控制结构

2 智能补偿滑模控制系统数学模型

系统中的RBFN 估计器用于在线估计集总不确定度H，它是由L 个传感单元组成的RBFN 神经网络，可划分为输入层、隐含层和输出层﹒在RBFN 中，为减少FPGA 的计算量，每层节点的传感器函数均选择三角函数﹒RBFN 神经网络结构及其隐含层的三角隶属函数如图3 所示﹒

图2 基于ICSMC 算法的PMLSM 智能控制伺服系统组成结构

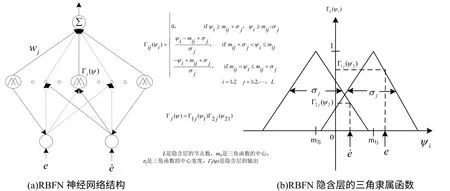
图3 RBFB 神经网络的组成及其隐含层的隶属函数

在RBFN 输出层，使用权重和的方法来计算RBFN 的输出，其输出可表示为

3 ICSMC 系统仿真模型

利用Matlab/Simulink R2018a 对智能控制伺服系统ICSMC 进行数学建模﹒建模使用自顶向下分解系统/模块和自底向上分层构建模块/系统的方法，以Simulink 模块为主、自建S 函数封装而成的模块为辅，通过原理图的形式构建各层次的模块/系统﹒

图4 为PMLSM 智能控制伺服系统仿真的总体组成结构，它包括ICSMC 系统和PMLSM 驱动系统子模块﹒图5为ICSMC系统仿真的内部模块组成结构，它主要包括滑模面产生器、RBFN 神经网络和ICSMC 控制律﹒仿真模型的主要参数如下：A_n=−42.250 398 724 082 93，B_n=0.006 27，M=0.125 4，K_f=20，α =2，λ=8﹒

图4 PMLSM 智能控制伺服系统总体仿真结构

图5 ICSMC 系统仿真的内部模块结构

4 ICSMC 系统仿真结果分析

当给定位移期望轨迹dm分别为正弦信号和梯形波信号时，ICSMC 位移轨迹跟踪如图6～图7所示﹒从图6～图7 可以看出，实际跟踪位移轨迹d 与给定位移期望轨迹dm几乎重合，具有非常好的跟踪效果﹒ICSMC的控制电压输出如图8～图9所示﹒从图8～图9 可看出，控制电压u 经过不到2 个时钟周期的波动便达到了稳定状态﹒ICSMC位移跟踪轨迹误差如图10～图11 所示﹒从图10～图11 可以看出，位移跟踪轨迹误差e 也经过不到2 个时钟周期的波动便达到了稳定的状态﹒位移跟踪轨迹误差从开始的波动状态到稳定状态，在输入正弦波形时，其波动幅度在4%左右；而输入梯形波形时，其波动幅度在5%左右﹒

综合以上仿真分析结果可知，对于周期性正弦期望轨迹和梯形期望轨迹的跟踪，ICSMC 智能控制伺服系统具有响应速度快、基本无超调和抗干扰能力强的特点，并具有良好的动态性能和较强的鲁棒性﹒

图6 ICSMC 位移轨迹跟踪(给定位移期望轨迹dm 为正弦信号)

图7 ICSMC 位移轨迹跟踪(给定位移期望轨迹dm 为梯形信号)

图8 ICSMC 控制电压输出(给定位移期望轨迹dm 为正弦信号)

图9 ICSMC 控制电压输出(给定位移期望轨迹dm 为梯形信号)

图10 ICSMC 位移跟踪轨迹误差(给定位移期望轨迹dm 为正弦信号)

图11 ICSMC 位移跟踪轨迹误差(给定位移期望轨迹dm 为梯形信号)

5 结论

为提高PMLSM 伺服驱动系统控制性能，给出了一种将模糊控制、神经网络、滑模控制和自适应学习相结合的智能补偿滑模控制算法，建立了基于该算法的智能补偿滑模控制系统(ICSMC)模型，实现了对PMLSM 伺服驱动系统动子跟踪周期参考轨迹的高性能控制﹒在Matlab/Simulink软件环境下的仿真结果表明，ICSMC 系统响应速度快、基本无超调、抗干扰能力强，且具有良好的动态性能和较强的鲁棒性﹒