具有参数切换的随机中立型神经网络自适应指数同步
代安定,叶雨辰,杨建光
(湖南城市学院 理学院,湖南 益阳 413000)
近10 几年来,神经网络的混沌同步因其在化学和生物系统、保密通信和信息科学等领域的潜在应用而被人们广泛地研究与关注[1-2]﹒为了使神经网络实现同步,学者们提出了许多有效的控制方法,比如反馈控制、自适应控制和脉冲控制等,自适应控制因具有参数自动更新的优势而倍受关注﹒
由于信号传输速度有限,时滞经常出现在生物神经网络和人工神经网络中﹒同时,时滞也是引起神经网络系统不稳定或振荡的源头﹒为此,许多研究者通过找到时滞依赖的充分性条件,以保证时滞神经网络实现全局渐近稳定和指数稳定等[3-8]﹒另外,最近研究发现,在许多动态系统中,不仅系统状态中存在时滞,而且系统状态的变化率中也存在时滞[5]﹒如化学反应器、输电线路和超大规模集成系统中部分元件的等效电路以及Lotka-volterra 系统等﹒在应用超大规模集成电路实现神经网络时可能存在中立型时滞,因此,研究含中立型时滞神经网络的稳定性和同步问题是非常有意义的﹒在现实世界中,神经质释放的波动和其它随机性因素可能会影响神经网络的稳定性,所以将噪声扰动加入神经网络模型中,会使得同步结果更加普遍和符合实际[6,8]﹒
研究拟在中立型神经网络模型中加入参数不确性和随机噪声干扰,并考虑其均方指数同步问题﹒在时滞是有界可测的前提下,基于Lyapunov稳定性原理提出2 个保证中立型神经网络实现同步的时滞依赖的充分性判据,并设计出依赖Markovian 跳变的自适应更新律﹒
1 问题描述


2 主要结果



3 数值仿真

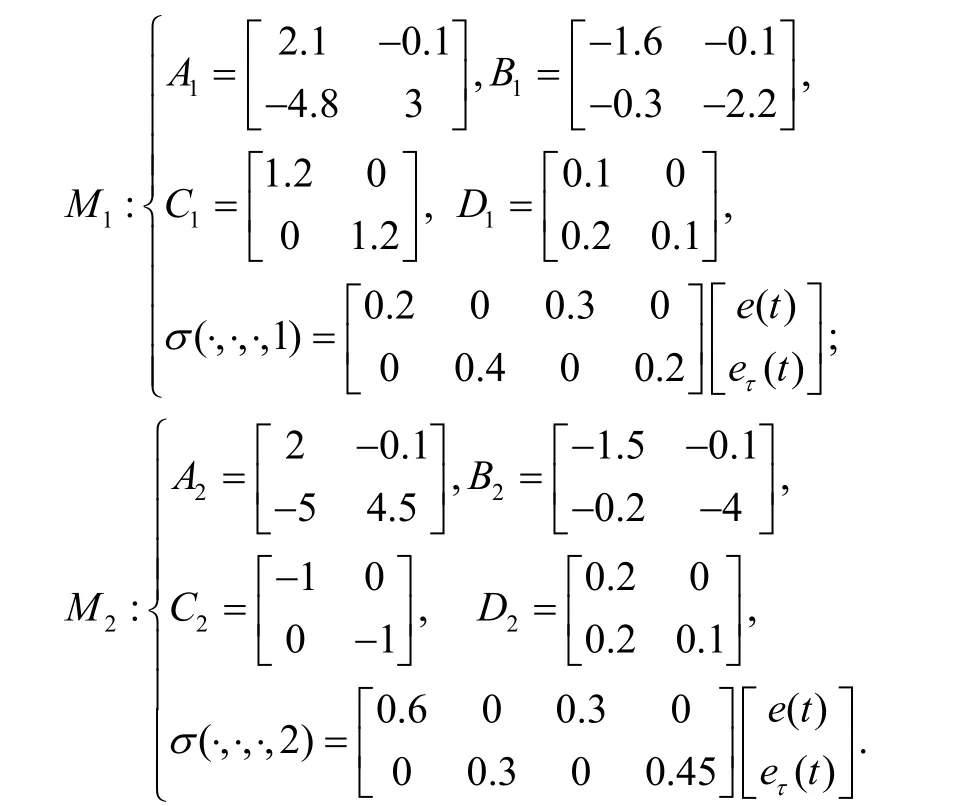
系统数字仿真结果如图1~图5 所示﹒
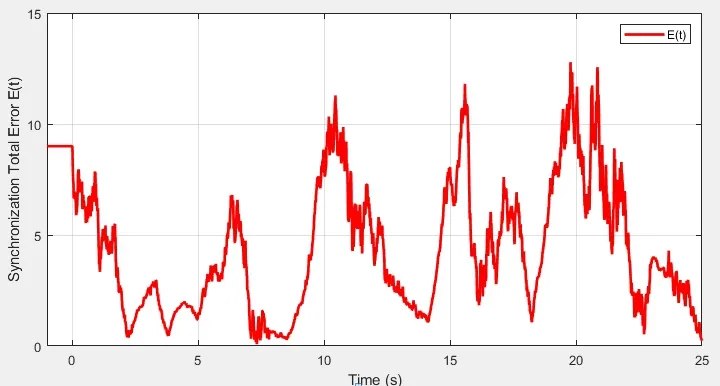
图1 未施加控制时,驱动-响应系统的同步总误差轨迹
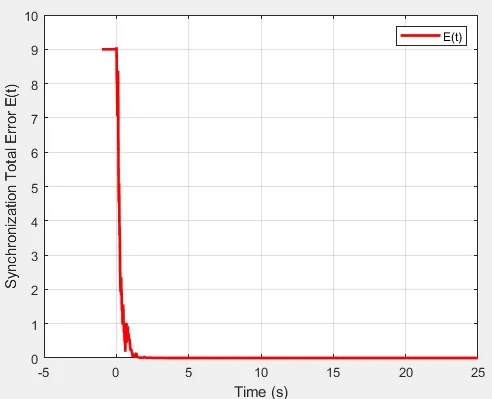
图2 施加控制后,驱动-响应系统的同步总误差轨迹
根据定理1,自适应更新律设为
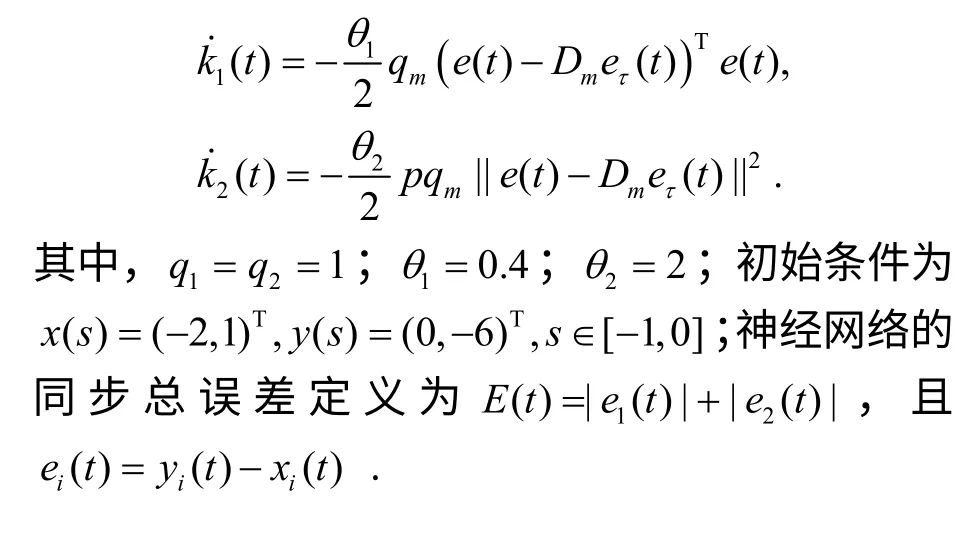

图3 反馈增益随时间的演变轨迹
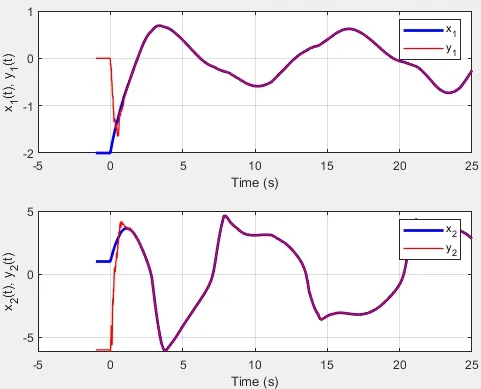
图4 施加控制时,驱动-响应系统的状态轨迹

图5 自适应控制下驱动-响应系统在平面的轨迹
从图1 中可看出,驱动-响应系统在没有施加控制时,是无法达到同步的;从图2、图4 和图5可看出,施加自适应控制后,系统可实现同步﹒
4 结论
研究了具有Markovian 切换中立型神经网络的同步问题,给出了保证驱动-响应神经网络达到同步的充分性条件,同时还提出了一种自适应更新律的设计方案并通过实例验证了其准确性﹒

