跟驰行驶状态下的驾驶模拟有效性研究

张彦宁，郭忠印，李振江

（1.同济大学道路与交通工程教育部重点实验室，上海201804；2.山东省交通规划设计院，山东济南250031）

为了创造安全的驾驶环境并采集特定驾驶场景下的驾驶行为数据，驾驶模拟技术得到了广泛的运用。作为使用这项技术的前提条件，驾驶模拟的有效性也越来越受到交通研究者的关注。Blana［1］指出驾驶模拟平台所提供的是没有现实映射的、人工制造的驾驶环境，模拟驾驶环境中的任何差异均可能造成驾驶员行为发生变化。因此，在驾驶模拟器中观察到的任何性能指标均有可能与实际情况的不一样。为了控制驾驶行为差异，首先需要验证驾驶模拟技术的有效性。同时Matowicki［2］指出不同驾驶模拟场景之间有效性结论并不通用，不同驾驶模拟场景的有效性验证最好独立进行。

目前，驾驶模拟的有效性通常被划分为绝对有效性和相对有效性［3］。绝对有效性指实车驾驶获得的分析指标与模拟驾驶获取的分析指标在数值上相等。相对有效性指模拟驾驶结果产生与实车驾驶结果相似的效果或相同的趋势。研究通常通过分析驾驶模拟平台的绝对有效性和相对有效性证明实验以及研究的合理性。例如Riener［4］通过对比驾驶员的反应时间，验证了驾驶模拟器在反应时间研究上的相对有效性。研究发现在模拟实验和实际驾驶中驾驶员的反应模式类似，但由于实际驾驶的环境复杂性，驾驶员在实际驾驶时的反应时间稍稍超过模拟驾驶时的反应时间。Tornros［5］使用驾驶模拟器研究了隧道驾驶安全，通过对比车辆在隧道中的行驶速度与横向偏移，证实驾驶模拟技术在研究该类问题上具备相对有效性。研究发现驾驶员在两种不同实验环境下驾驶行为存在差异，即驾驶模拟实验中车速相对较高、驾驶模拟实验中车辆在弯道横向偏移较大。Risto［6］分析驾驶员跟驰行为后认为两种不同驾驶条件下驾驶员的安全跟驰距离不存在统计显著差异，即驾驶模拟在该行为研究中有绝对有效性。进一步，研究者在验证驾驶模拟器有效性的过程中构建了驾驶行为差异的修正方法。例如，Llopis-Castelló［7］通过自然驾驶数据与模拟实验数据的对比分析得出了驾驶模拟平台的速度参数修正方法，并搭建了低成本驾驶模拟平台。上述研究均基于其研究目的验证了驾驶模拟器的有效性，本文将针对跟驰行为进行专门的驾驶模拟有效性验证。

目前驾驶模拟绝对有效性的判别方法以数据的直接对比［5］以及统计检验为主［8］，相对有效性通过实验设计、观察指标随自变量变化趋势进行验证［3］，目前尚未有统一的验证方法与验证指标。生存分析是一种研究多种因素的、既考虑时间又考虑结果的统计方法［9］，可以用于驾驶员反应时间等时间数据的有效性验证。本文参考已有研究，首先设计了实车实验与驾驶模拟实验。选取了多种跟驰行为指标，使用Wilcox检验方法、线性回归分析非时间数据有效性，使用生存分析方法分析时间数据有效性。对检验结果、生存分析结果进行分析，最终得出结论为其他驾驶模拟研究提供理论前提。

1 实验方案

1.1 实验设备

1.1.1 实车实验设备

实车实验中使用整合了惯导系统、GPS以及数据处理系统的实验车，见图1，采集车辆位置、速度以及加速度数据。其中车载数据处理系统可对采集得到的原始数据进行时间同步等初步处理。车载惯导系统、车载GPS的数据采集频率均为10Hz。

1.1.2 驾驶模拟实验设备

通过同济大学高仿真度的驾驶模拟平台及配套的SCANeRTM驾驶模拟软件实施驾驶模拟实验。驾驶模拟平台拥有八向自由度运动平台，驾驶舱内搭建250°环形屏幕和音响系统，舱内放置小型车实车并改装传感仪器。模拟平台可以模拟各种交通环境，配合SCANERTM软件及驾驶舱内小型车上安装的传感仪器可采集驾驶员的驾驶行为数据以及车辆状态数据。本实验采集数据包括车辆位置、速度、加速度信息，数据的采集频率为100Hz，输出为10Hz。

图1 实验设备Fig.1 Experiment equipments

1.2 实验环境

实车实验路段位于山东省某高速公路，实验路段为双向四车道高速公路、限速为100km·h-1、全长10km。对应实车实验场景，在驾驶模拟软件中构建了相同线形的模拟场景。

1.3 实验人员

实车实验和驾驶模拟实验均按照以下要求招募驾驶员：拥有合法驾驶执照；超过实习期；有日常驾驶经验。为了避免年龄、驾驶经验等驾驶员特质对实验结果产生干扰，参照Davenne［10］的实验人员招募方案招募了两批相似条件的驾驶员，对驾驶员年龄和驾驶经验进行了控制。最终招募了36名男性驾驶员，实车驾驶实验20名驾驶员，平均年龄25.4岁，标准差3.5岁，平均驾龄3.3年，标准差1.5年；模拟实验16名驾驶员，平均年龄25.6岁，标准差2.4岁，平均驾龄3.7年，标准差1.1年。

1.4 实验流程

吴斌［11］的研究表明激进的跟驰行驶过程中追尾事故的发生风险较高。Paolo［12］指出跟驰过程中，前车突然加减速将导致追尾事故发生。参考上述跟驰研究，实验设计中包含加减速跟驰以及稳定跟驰的情况。实验中要求后车驾驶员跟随前车行驶并根据自己的判断保持安全距离。前车根据研究者指令行驶，并全程保持车道行驶。根据指令，前车在每个速度保持一定时间的稳定行驶后再进行加、减速，前车以20 km·h-1为梯度逐级加、减速，速度范围为40 km·h-1～80 km·h-1。

2 有效性判别指标及判别方法

2.1 有效性判别指标

跟驰距离是表示前后车跟驰状态时推荐使用的指标［13］，驾驶员的反应延迟时间是影响跟驰行为预测的重要参数。为了表达跟驰行驶状态下的驾驶行为并对比得出驾驶模拟实验中驾驶行为的有效性，选择了跟驰距离、跟驰距离标准差、车头时距以及驾驶员跟驰反应延迟时间作为驾驶模拟有效性的分析指标。

2.1.1 跟驰距离

跟驰距离d指跟驰过程中前车和后车所保持的相对距离的平均值。跟驰距离表示了后车驾驶员为了维持目前的跟驰状态所能接受的与前车之间的安全距离。

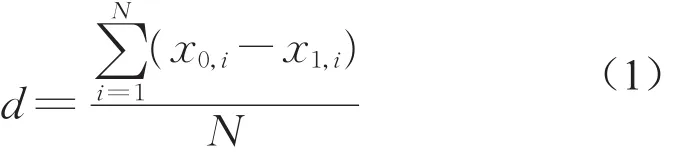
式中：x0，i和x1，i指前车和后车在时刻i时的位置。

2.1.2 跟驰距离标准差

跟驰距离标准差σd指跟驰行驶状态持续过程中，跟驰距离的标准差。跟驰距离标准差表示了后车驾驶员的行驶稳定性。当后车驾驶员驾驶稳定性较差时，其将通过频繁的加减速调整与前车之间的距离，即跟驰距离标准差更大。

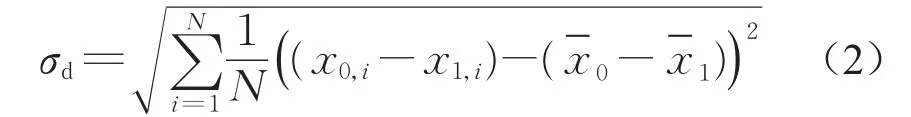
2.1.3 车头时距

车头时距指跟驰过程中前车和后车之间车头时距的平均值。

2.1.4 跟驰反应延迟时间

跟驰反应延迟时间指前车行驶状态发生改变（即前车加减速特征点）到后车行驶状态发生相应改变（即后车加减速特征点）的时间间隔，包含后车驾驶员的感知、识别、决定以及动作反应时间，表示后车受前车刺激后做出相应跟驰行为的全部过程。

2.2 跟驰状态特征点识别

2.2.1 跟驰状态

基于Zhang［14］的研究，以前后车加减速度变化点为跟驰行驶状态起止的识别点，跟驰行驶状态定义见图2，减速点识别示意图见图3。以减速点为例：

减速起始点识别：

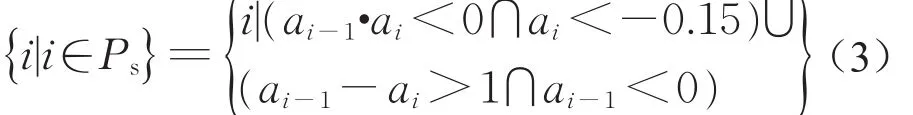
减速终止点识别：

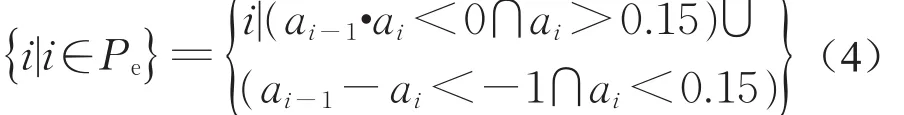
式中：Ps为减速起始点集合；Pe为减速终止点集合；ai为断面i的车辆加速度，m·s-1；ai-1为断面i的上一断面车辆加速度，m·s-1。

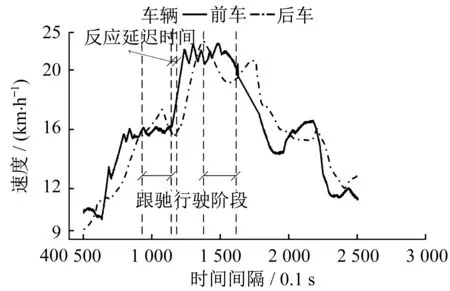
图2 跟驰行驶状态Fig.2 Car-following status

图3 减速特征点Fig.3 Deceleration point

2.2.2 反应延迟特征点

驾驶员延迟时间可通过前后车加、减速变化点识别［14］，见图1。以前车加、减速变化点为延迟时间起点，后车加、减速变化点为终点，加、减速变化阈值为±0.15m·s-2。

2.3 有效性判别方法

驾驶模拟实验的有效性分为绝对有效性及相对有效性［3］。绝对有效性指两种实验条件下的判别指标不存在统计显著的差异，相对有效性指两种实验条件下判别指标数值虽然存在显著差异但判别指标的变化规律相同。设计了2×3实验（2种驾驶环境×3种跟驰速度）分析跟驰距离、跟驰距离标准差、车头时距随跟驰速度的变化规律，同时可以分析驾驶员反应延长时间随前车加减速状态的变化规律。

2.3.1 Wilcox秩和检验

Wilcox秩和检验是一种非参数检验方法，可用于样本均值的成对比较。其零假设为：两个样本均值之间没有显著差异。使用Wilcox秩和检验分析实际驾驶条件下的有效性判断指标与模拟驾驶条件下的有效性判断指标之间是否存在显著性差异，即分析判别指标的绝对有效性。

2.3.2 基于生存分析的有效性判别

生存分析作为一种概率统计分析方法，用于分析有一定持续时间、具备事件结局的数据。针对驾驶员反应延迟时间这一时间数据，提出使用生存分析方法判断反应延迟时间的绝对有效性及相对有效性。根据生存分析的基本概念［15］，生存分析要素包含事件、事件生存时间t、事件结局δ、事件的生存函数S(t)以及事件的风险函数h(t)。

（1）事件：事件的时间起点为识别前车加减速特征点的时刻，事件终点为识别后车加减速特征点的时刻，描述从前车加减速到后车驾驶员对其做出反应的过程。

（2）事件生存时间：事件生存时间t即反应延迟时间，为前车加减速特征点到后车加减速特征点间经历的时间。

（3）事件结局：事件结局δ表示后车加减速特征点是否被识别，当没有识别出后车加减速特征点时认为事件失效，δ=1，当识别后车加减速特征变化点时认为该事件删失，δ=0。

（4）生存函数：延迟时间的生存函数S(t)表示在前车加减速特征点被识别t时间后后车加减速特征变化点还未被识别的概率，即已知延迟时间超过t的概率。

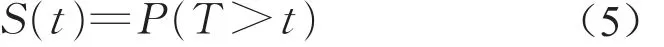
（5）风险函数：事件的风险函数h(t)表明前车加减速特征点被识别后t到t+Δt时间内后车加减速特征点被识别的瞬时概率，见式（6）。

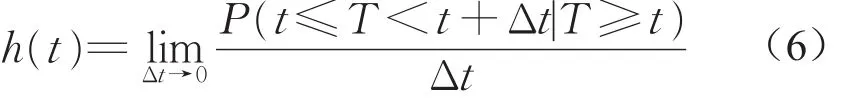
采用Kaplan-Meier方法估计反应延迟时间的生存函数。Kaplan-Meier生存函数S^(t(j))的估计方法见式（7）。

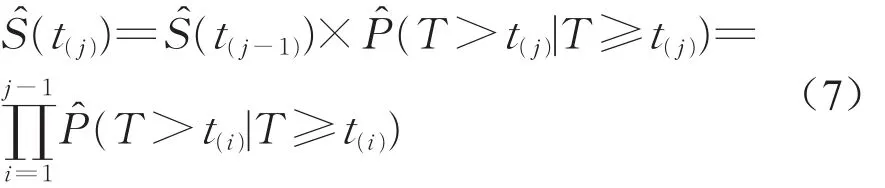
式中S^(t(j))为延迟时间为t(j)时采用Kaplan-Meier方法估计的生存函数，t(j)为将延迟时间从小到大按顺序排列后的第j个值，P^(T＞t(j)|T≥t(j))为当延迟时间达到t(j)且大于t(j)的概率。

采用Log-rank方法检验时间数据的绝对有效性。Log-rank方法是一种基于生存曲线的统计检验方法，用于检验两条生存曲线（即两组反应延迟时间的生存曲线）之间是否存在显著性差异，当生存曲线之间不存在显著性差异时认为指标具备绝对有效性。

当时间数据不满足绝对有效性时，采用Cox回归方法检验数据的相对有效性。Wynne［3］指出当实际环境、模拟环境中指标随影响因素的变化趋势相同时，则可认为该指标具备相对有效性。在Cox回归中，相对有效性表现为实车实验模型、模拟实验模型对应参数的回归系数符号相同。Cox回归模型表达形式如下：

式中：X为延迟时间影响因素自变量向量，βi为回归系数，h0(t)为延迟时间的基准风险函数。

3 实验结果与分析

3.1 跟驰距离有效性

表1中结果表明实际驾驶环境中跟驰距离相比模拟驾驶环境中跟驰距离大2.57m，比例为5.5%。其中前车速度为40 km·h-1时大0.10m，比例为0.3%，前车速度为60 km·h-1时大0.15m，比例为0.3%，前车速度为80 km·h-1时大4.22m，比例为5.7%。Wilcox秩和检验结果表明不同驾驶环境之间的跟驰距离差异不显著（p=0.714），跟驰距离具备统计显著的绝对有效性。

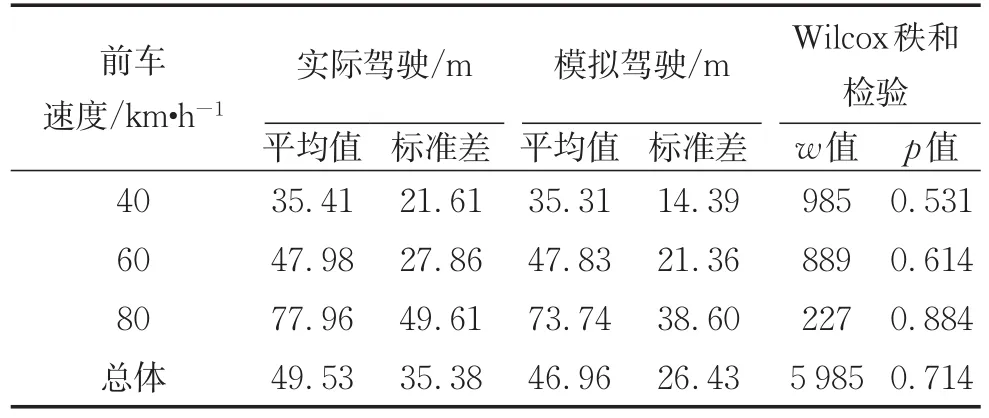
表1 跟驰距离有效性检验结果Tab.1 Car-following distance validity test result

3.2 跟驰距离标准差有效性

表2中结果表明实际驾驶环境中跟驰距离标准差相比模拟驾驶环境中跟驰距离标准差小1.7m，比例为30.2%。其中前车速度为40 km·h-1时小0.93m，比例为23.3%，前车速度为60 km·h-1时小1.79m，比例为30.5%，前车速度为80 km·h-1时小3.93m，比例为43.0%。Wilcox秩和检验结果表明不同驾驶环境之间的跟驰距离标准差差异显著（p=0.000）。其中前车速度为40 km·h-1、60 km·h-1、80 km·h-1时，Wilcox秩和检验p值分别为 0.001、0.006、0.014，两种不同实验环境之间的跟驰距离标准差均存在显著差异。图4表明不同驾驶环境中跟驰距离标准差受前车速度影响趋势相同，即前车速度越大跟驰距离标准差越大，驾驶员驾驶稳定性越差。线性回归结果表明该变化趋势显著，实际驾驶条件下前车速度回归系数0.057（p=0.008），模拟驾驶条件下前车速度回归系数0.125（p=0.000）。综上，跟驰距离标准差具备统计显著的相对有效性。

图4 不同实验环境-前车车速的跟驰距离标准差Fig.4 Car-following distance standard deviation under different condition

表2 跟驰距离标准差有效性检验结果Tab.2 Car-following distance standard deviation validity test result

3.3 车头时距有效性

表3中结果表明实际驾驶环境中车头时距相比模拟驾驶环境中车头时距大0.12s，比例为3.9%。其中前车速度为40 km·h-1时小0.01s，比例为0.3%，前车速度为 60 km·h-1时大 0.10s，比例为3.5%，前车速度为 80 km·h-1时大 0.40s，比例为12.2%。Wilcox秩和检验结果表明不同驾驶环境之间的车头时距差异不显著（p=0.570），车头时距具备统计显著的绝对有效性。

表3 车头时距有效性检验结果Tab.3 Headway validity test results

3.4 跟驰反应延长时间有效性

Kaplan-Meier生存曲线估计结果以及对应的log-rank检验结果见图5。当log-rank检验结果p＞0.05时，认为实际驾驶的反应延迟时间生存曲线与模拟驾驶的反应延迟时间生存曲线之间的差异在95%的置信水平下不显著，反应延迟时间具有绝对有效性。图5结果表明跟驰反应延长时间在不同实验环境下不存在显著差异（p=0.800），即反应延迟时间具备绝对有效性。其中除前车车速为80 km·h-1时模拟驾驶环境中反应延迟时间较高外（p=0.002），前车车速40 km·h-1（p=0.900）、前车车速60 km·h-1时（p=0.200）不同实验环境下驾驶员反应延迟时间没有显著差异。

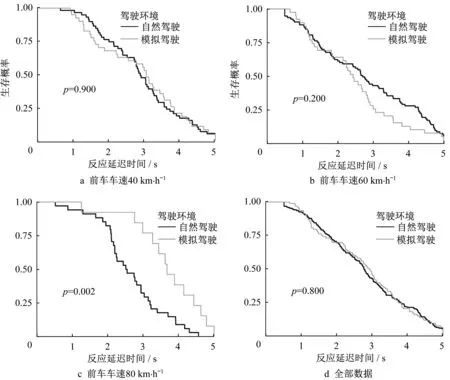
图5 Kaplan-Meier生存曲线估计结果Fig.5 Kaplan-Meier survival curve estimation result

Log-rank检验结果已经证明反应延迟时间具备绝对有效性，在此通过Cox风险模型估计结果说明影响因素与反应延迟时间的相关关系。Cox风险比例模型的自变量定义见表4。Cox风险比例模型结果见表5，在实际驾驶环境中反应延迟时间受前车加速度、前后车相对距离、前车加速度变化状态的显著影响（p=0.001，p=0.005，p=0.005）。前车加速度的回归系数为-0.508，风险比例为0.601，表明相比前车减速，当前车加速运动时延迟时间风险函数h(t，X)减小39.86%，即前车减速运动时驾驶员反应延迟时间较短。前后车相对距离的回归系数为-0.009，风险比例为0.991，表明每当前后车相对距离增加1m（10m）时延迟时间风险函数h(t，X)减小0.89%（8.55%），即前后车相对距离越小驾驶员延迟时间越短。前车加速度变化状态回归系数为-0.463，风险比例为0.629，表明相比前车由匀速运动变为变速运动的情况，当前车由变速运动变为匀速运动时延迟时间的风险函数h(t，X)减小35.39%，即前车由匀速运动变为变速运动时驾驶员的延迟时间较短。而模拟驾驶环境中驾驶员的反应延迟时间受自变量影响并不显著，结合Log-Rank检验结果，在反应延迟时间具备绝对有效性的前提下需要进一步实验验证自变量对驾驶员反应延迟时间的影响。

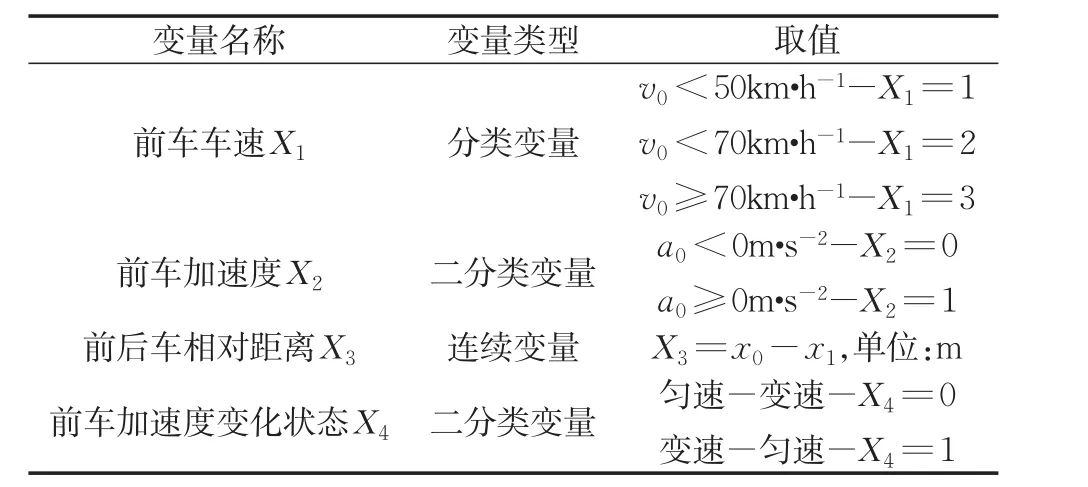
表4 延迟时间Cox模型自变量定义Tab.4 Delay time Cox model independent variable definition

表5 基于Cox回归的驾驶模拟相对有效性分析Tab.5 Driving simulation relative validity analysis based on Cox regression model

4 结语

通过对比实车实验与驾驶模拟实验，分析了跟驰行驶状态下车辆跟驰距离、距离标准差、车头时距以及驾驶员反应延迟时间的有效性。结果表明跟驰距离、车头时距、驾驶员反应延长时间均具有绝对有效性，跟驰距离标准差具有相对有效性。进一步的Cox模型结果表明，实际驾驶环境下驾驶员反应延长时间受前车加速度、前后车相对距离、前车加速度变化状态的显著影响。有效性研究成果可为研究者利用驾驶模拟平台进行其他跟驰行为研究提供基本前提。Cox模型成果用于驾驶员反应延迟时间建模及跟驰模型优化。

研究过程中发现了一些问题需要通过进一步研究来解决：实验路段为高速公路的一般路段，然而小半径曲线、长大纵坡等典型路段也是影响驾驶员驾驶行为的因素之一，道路线形与实验环境等因素之间可能存在复杂的耦合关系，从而影响驾驶行为表达的差异性。下一步可针对道路线形等影响因素提出针对性的实验方案并进行深入研究。