硫酸盐侵蚀后地铁盾构隧道纵缝接头抗弯力学模型

郑勇波，白廷辉，李晓军

（同济大学土木工程学院，上海 200092）

地铁盾构隧道的主体混凝土结构外侧处于地下水丰富、透水性强的地层中，富含氯离子、硫酸根离子等侵蚀性介质［1］。管片混凝土被硫酸盐侵蚀后产生钙化，强度降低，受力截面积减少，导致纵缝接头的受力和变形形式呈现明显的非线性特性。

研究混凝土被硫酸盐侵蚀对纵缝接头力学性能的影响，本构关系是基础，姜英波、梁岩及徐善华等［2-5］等已经开展了不少研究，获得了较为可靠的劣化后混凝土本构关系及参数。正常状态下盾构纵缝接头抗弯力学性能的研究方法可做参考，常用的有理论解析、数值模拟及足尺试验等三种分析方法，其中理论解析及数值模拟方法相对成本较低，更为实用。闫治国、Li及刘四进等［6-9］通过设定接缝面混凝土受压区形状，以接头接触关系为基础构件解析力学模型，分析接头抗弯受力性能。郭瑞、庄晓莹及汪亦显等［10-12］建立管片接头三维数值模型，采用不同材料本构，研究纵缝接头抗弯刚度以及压弯后受力及破坏全过程状态。Ding、Gong和Liu等［13-15］开展管片接头足尺试验，研究接头力学性能、裂缝发展过程及极限承载力。由上可知，针对正常状态下盾构隧道纵缝接头的力学模型和数值计算已有不少成果，部分理论和方法可借鉴使用，但全部直接应用到混凝土劣化后纵缝接头力学性能分析中还存在不少问题。一是没有考虑混凝土劣化后的材料本构关系变化、应力分布不连续及有效受力面积变化等因素，二是无法针对性地考虑因盾构隧道腐蚀特性而引起的更为复杂的接头截面应变关系。因此，亟需在现有成果基础上，进一步研究以获得更适用混凝土劣化后的盾构隧道纵缝接头力学模型。

基于混凝土被硫酸盐侵蚀主要发生于管片外表面的实际情况，考虑接缝面构造、混凝土非线性受力特性、接缝面荷载传递特性以及螺栓预紧作用等因素，本文建立了适合分析混凝土劣化后纵缝接头抗弯性能的力学模型，对不同侵蚀程度的纵缝接头抗弯力学性能进行全过程探索性研究，并与数值计算结果进行对比，得到可供实际工程借鉴的研究成果。

1 纵缝接头抗弯力学模型建立

1.1 模型基本假定

（1）接头离散为四个不同功能部件，分别为外表面边缘混凝土、受压区混凝土、螺栓及内表面边缘混凝土，具体如图1所示。接头变形主要由不同区域混凝土压缩及螺栓受拉等变形引起，不考虑管片自重及端肋影响；

（2）受力后接头截面逐渐形成脱离区与压紧区，均满足平截面设定。压紧区混凝土全截面受压，脱离区不同离散构件各自形成平面；螺栓应变与混凝土应变则根据接头受力状态取不同构件平面计算；

（3）混凝土侵蚀层均匀分布且与正常层界限为平面，具体如图2所示。同时，侵蚀层与正常层的混凝土均设定为变形协调一致，满足平截面设定；

（4）螺栓预紧力等效为沿接缝截面均匀分布的压应力。螺栓只受拉不受压，混凝土只受压不受拉。

1.2 轴力荷载施加

螺栓预紧是在轴力加载前完成，因此，需考虑轴力加载对螺栓预紧状态的松弛效应。对纵缝接头施加螺栓预紧力nT0后，再施加轴力N，此时螺栓预紧力降为nT01，与受压区混凝土的合力Fc取得力学平衡，方程如下：

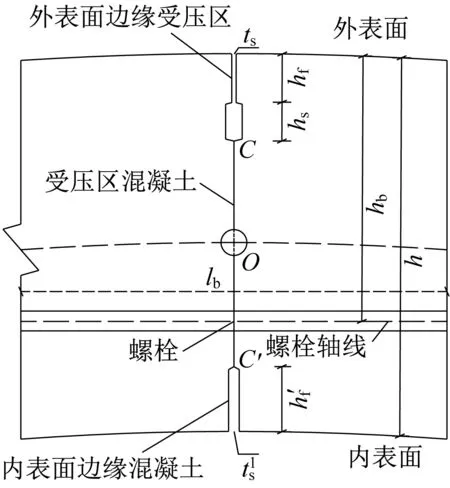
图1 纵缝接头部件构造Fig.1 Details of the longitudinal joint

图2 管片混凝土被硫酸盐侵蚀分布Fig.2 Distribution of sulfate attacked segmental concrete

螺栓预紧力等效为沿接缝截面均匀分布的压应力，轴力为非偏心加载，因此，受压区混凝土压应力为均布形式，可得

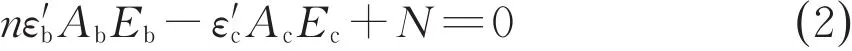
式中：n为螺栓个数；ε′b为轴力施加后螺栓残余应变；ε′c为轴力施加后受压区混凝土应变；Ab为螺栓截面面积；Eb为螺栓弹性模量；Ac为受压区混凝土截面面积；Ec为受压区混凝土弹性模量。

受压区混凝土因施加轴力产生的变形即是螺栓变形的变化量，则

式中：Δb0和Δ′b0分别为轴力施加前、后螺栓变形量，Δ′c0为轴力施加后混凝土变形量。

结合几何和物理方程，进一步推导可得

式中：T0为螺栓预紧力；lb为螺栓有效受拉长度；lcc为局部受压混凝土应力扩散等效长度，根据Li等［7-8］的结论，可取为0.55～0.7h。接着，联立式（2）及（4），即可求得ε′b及ε′c。当ε′b＞0时，螺栓仍处于受拉状态，对纵缝接头还残存预紧力，可以作为物理量放入后续弯矩加载计算中。当ε′b≤0时，螺栓已经处于松弛状态，忽略预紧力作用，即ε′b设为0。

1.3 正弯矩荷载施加

因混凝土被硫酸盐侵蚀发生在管片外表面，本文仅在正弯矩工况下分析其对纵缝接头力学性能的影响。取纵缝接头中性轴至外表面边缘处的距离yt及外表面边缘处混凝土的空隙量，作为不同正弯矩工况下纵缝接头力学状态的基本判据。

（1）力学状态1：Tb-Fc模式

在此力学状态下，纵缝接头所承受正弯矩较小，两侧外表面边缘混凝土尚未接触，同时，中性轴还未高过弹性密封垫底部，即＞0，yt＞hs+hf，如图3所示，其中，hs为弹性密封垫嵌缝高度，hf为外表面边缘受压区混凝土高度。根据图3，可得

式中：εc为受压区混凝土边缘压应变；εb为螺栓拉应变；hb为螺栓中心到外表面边缘距离；y为受压区混凝土高度。

图3 Tb-Fc模式的应变分布Fig.3 Strain distribution of(Tb-Fcmodel)

图4 所示的受压区和脱离区各功能部件的变形沿截面高度是线性变化的。依据下式（6）～式（10）进行计算，即

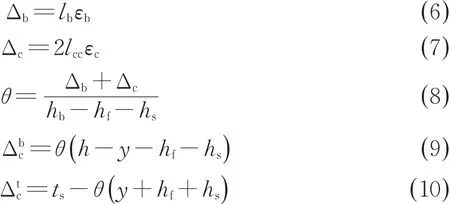
图4 Tb-Fc模式的几何变形Fig.4 Joint deformation(Tb-Fcmodel)

此时，螺栓是否开始受拉还需另外判断，εb为螺栓的拉应变，如果εb＜ε′b，则螺栓还未受拉，受压区混凝土单独受力；如果εb＞ε′b，则螺栓与受压区混凝土共同参与受力，如图5所示。

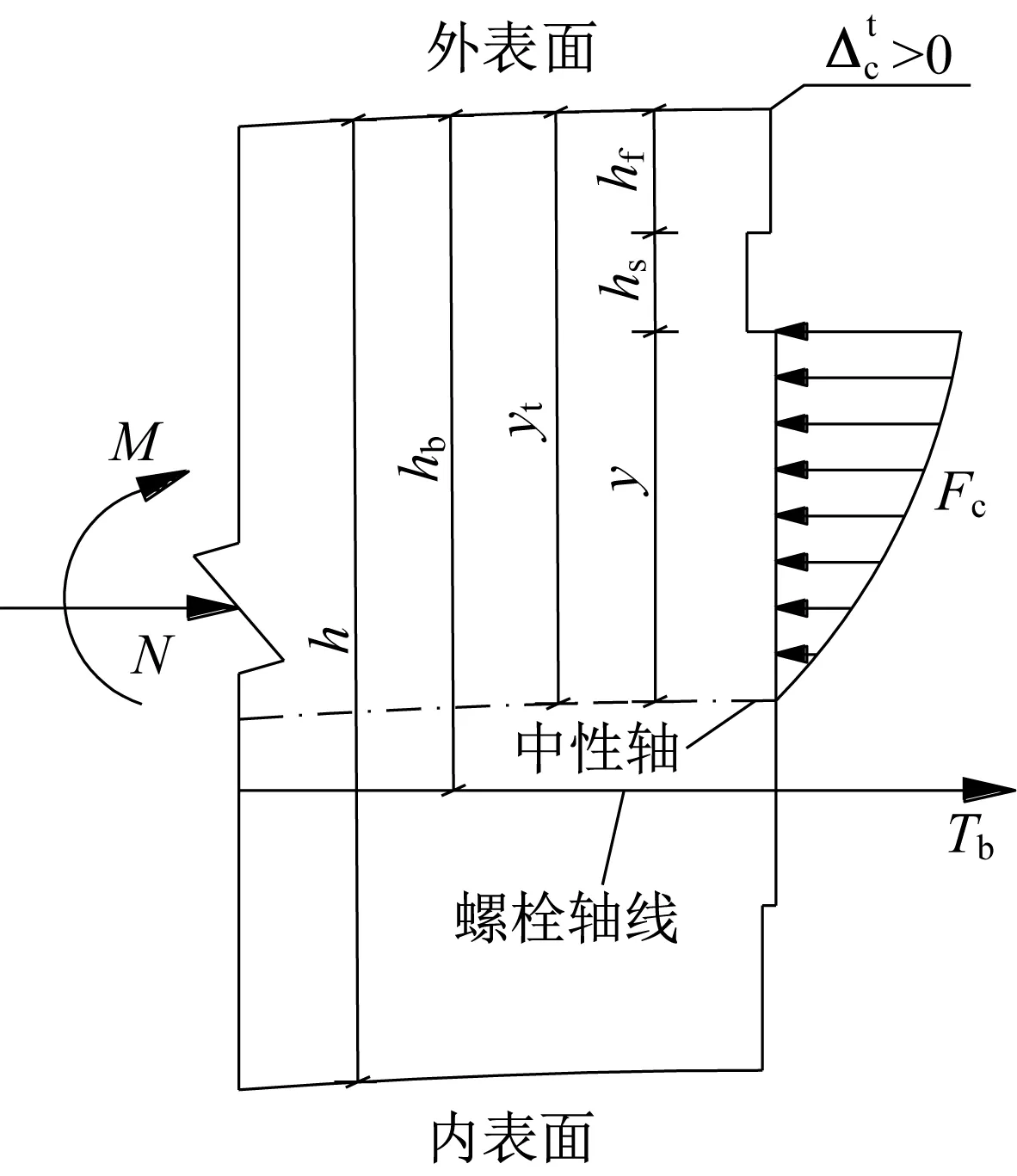
图5 Tb-Fc模式的受力平衡Fig.5 Equilibrium condition(Tb-Fcmodel)

以接缝截面形心O作为力矩转动点，可建立力学平衡方程如下：

式中：M为截面所受外部弯矩；N为截面所受外部轴力；Tb为螺栓拉力；Fc为受压区混凝土合力，参见式（13）计算；Mc为受压区混凝土合力对接缝截面形心O力矩，参见式（14）计算。

式中：x表示受压区混凝土应力积分点至接缝截面形心O的距离，偏向外表面为正，偏向内表面为负；σc表示正常混凝土压应力与x的函数关系；b为管片宽度；σc为正常混凝土的压应力函数。

（2）力学状态2：Tb-Fc-F0模式

在此力学状态下，纵缝接头所承受正弯矩进一步增大，两侧外表面边缘混凝土开始接触，同时，中性轴还未高过弹性密封垫底部，即Δtc＜0，yt＞hs+hf，如图6所示。

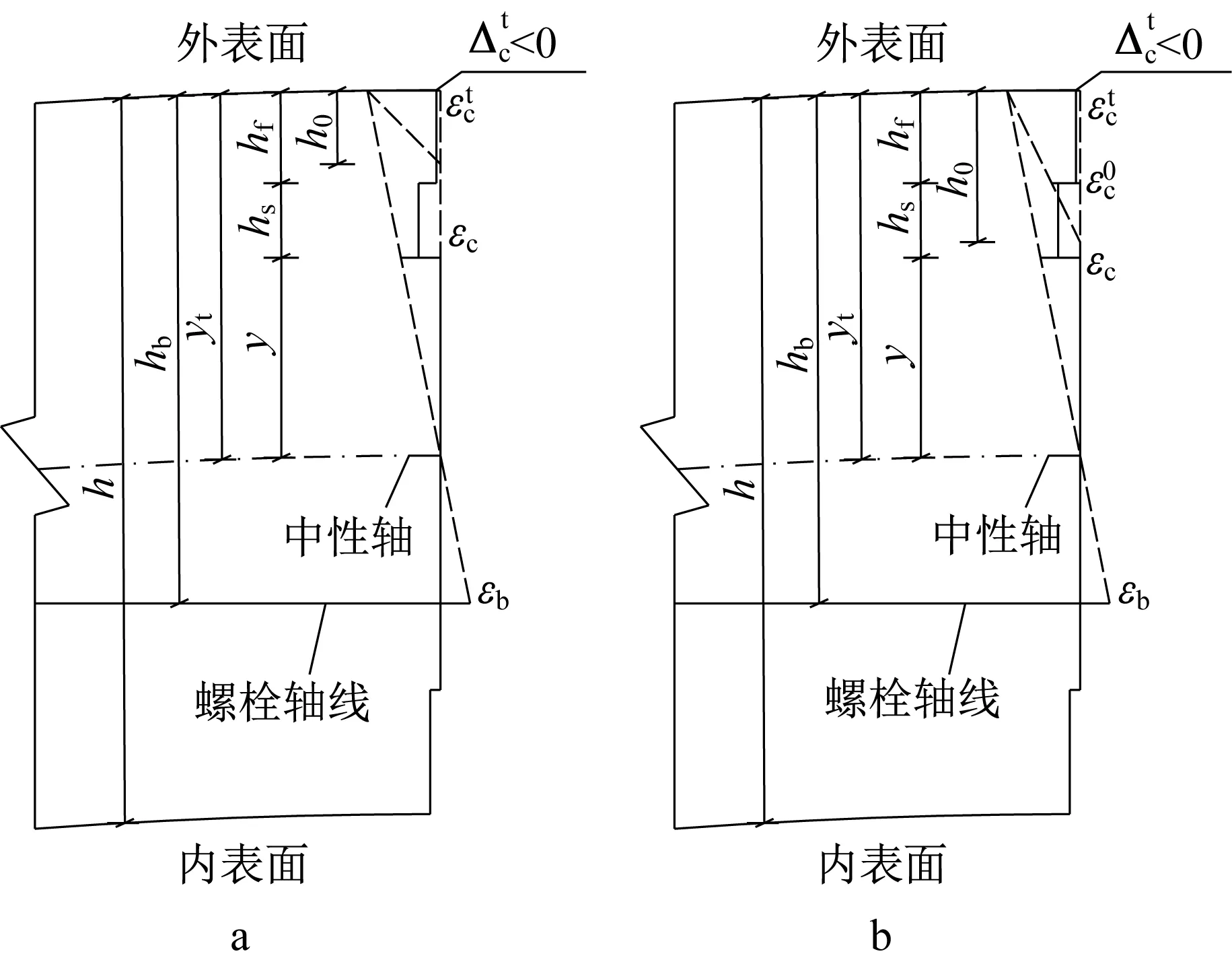
图6 Tb-Fc-F0模式的应变分布Fig.6 Strain distribution of(Tb-Fc-F0model)

根据图6，可得

式中：为外表面边缘混凝土压应变。

对于外表面边缘混凝土的应变关系，则根据外表面边缘混凝土受压区高度h0进行判断。h0的求解公式如下：

式中：h0为外表面边缘受压区高度。

特别地，当h0＞hf时，如图6b所示，需考虑外表面边缘受压区混凝土底部的等效压应变，其变形在h0高度范围内满足平截面假定，其关系如下：

图7所示的外表面边缘受压区和脱离区各功能部件的变形沿截面高度线性变化，Δb、Δc、θ等依据式（6）～式（10）进行计算。

图7 Tb-Fc-F0模式的几何变形Fig.7 Joint deformation(Tb-Fc-F0model)

此时，螺栓是否开始受拉还需另外判断，如果εb＜ε′b，则螺栓还未受拉，受压区混凝土单独受力；如果εb＞ε′b，则螺栓与受压区混凝土共同参与受力，计算简图见图8所示。

图8 Tb-Fc-F0模式的受力平衡Fig.8 Equilibrium condition(Tb-Fc-F0model)

以接缝截面形心O作为力矩转动点，可建立力学平衡方程如下：

式中：Fc及Mc参见式（13）和（14）计算；F0为外表面边缘混凝土合力，M0为内表面边缘混凝土合力对接缝截面形心O力矩，参见式（20）和式（21）计算。

如hd表示外表面边缘混凝土被侵蚀厚度，当h0≤hf时，外表面边缘混凝土受力平衡参如图9所示，其中，图9a表示hd≤h0的状态，图9b则表示hd＞h0的状态，由此可得F0及M0的计算如下：

式中：σd表示被硫酸盐侵蚀后混凝土压应力与x的函数关系。

图9 混凝土被硫酸盐侵蚀后的受力平衡（h0≤hf）Fig.9 Equilibrium condition 1(after concrete sulfate attacked)（h0≤hf）

当h0＞hf时，外表面边缘混凝土受力平衡如图10所示，其中，图10a表示hd≤hf的状态，图10b则表示hd＞hf状态，可得F0及M0的计算如下：

图10 混凝土被硫酸盐侵蚀后的受力平衡（h0＞hf）Fig.10 Equilibrium condition 2（after concrete sulfate attacked）（h0＞hf）

（3）力学状态3：Tb-F0模式

随着正弯矩继续增大，纵缝接头两侧外表面边缘混凝土仍然保持接触，同时，受压区混凝土完全脱离，且中性轴高过弹性密封垫顶部，即Δtc＜0，yt＜hs+hf，极端情况，甚至会出现螺栓被拉断或端肋脱落等破坏状态。当混凝土被压碎破坏时，纵缝接头已达正常使用极限状态，因此，此种工况出现表示接头进入承载力极限状态。

根据图11，可得

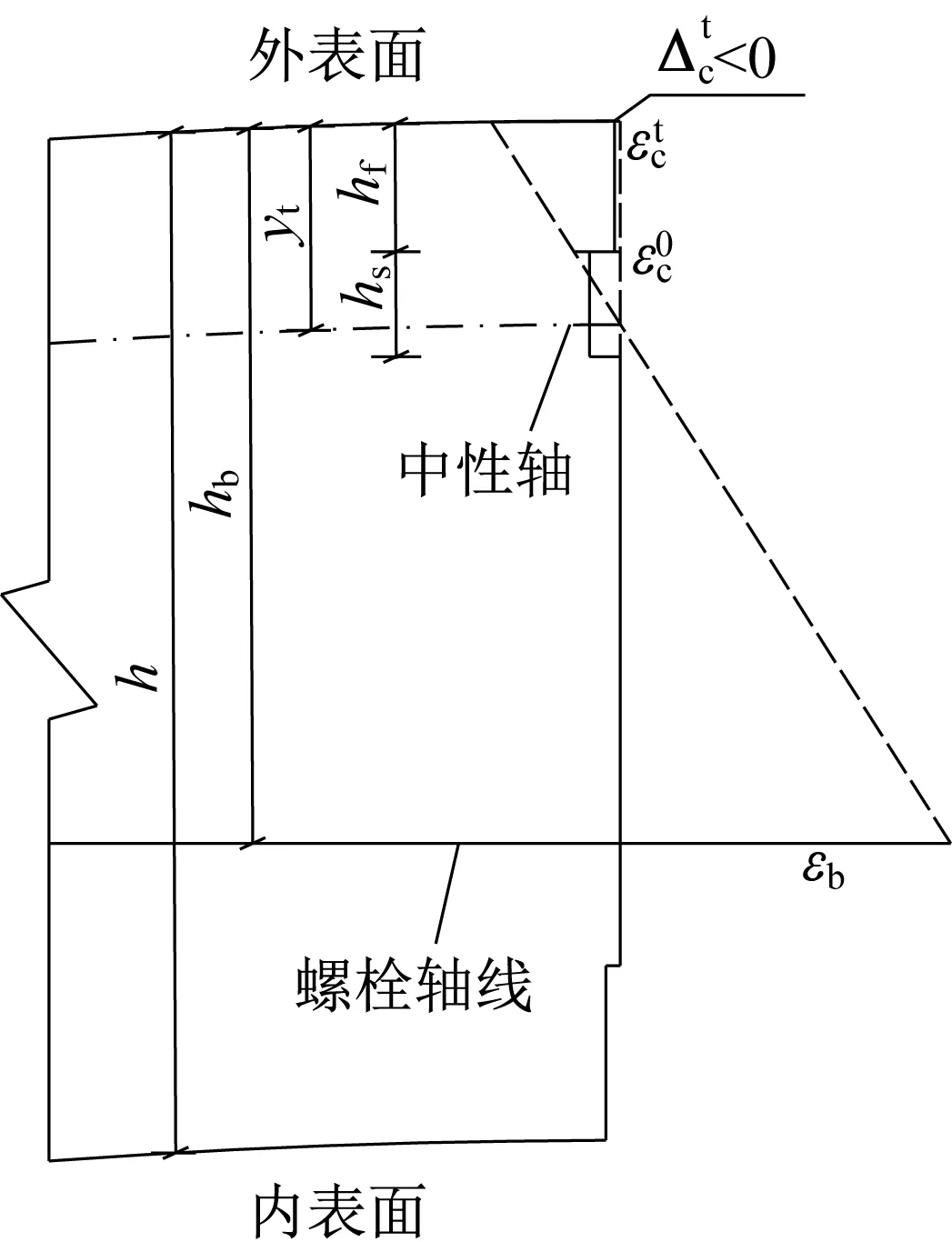
图11 Tb-F0模式的应变分布Fig.11 Strain distribution of(Tb-F0model)

图12 所示的外表面边缘受压区区和脱离区各功能部件的变形关系中，Δb及 Δc等计算参见式（6）及式（7），θ等变形量则依据式（25）～式（27）进行计算，即

以接缝截面形心O作为力矩转动点，可得

图12 Tb-F0模式的几何变形Fig.12 Joint deformation(Tb-F0model)

式中：F0参见式（20）计算；M0计算方法参见式（21）计算，计算简图见图13。

图13 Tb-F0模式的受力平衡Fig.13 Equilibrium condition(Tb-F0model)

2 混凝土被硫酸盐侵蚀后影响分析

2.1 计算参数设置

（1）混凝土

混凝土单轴受压应力应变曲线由二次抛物线和直线形组成，分为弹性段、强化段和软化段等三部分，取弹性极限点为0.4倍峰值应力［16-17］。

管片混凝土强度等级为C55，结合相关文献［2-5］的研究成果，正常及被硫酸盐侵蚀后混凝土的主要计算参数如表1所示。

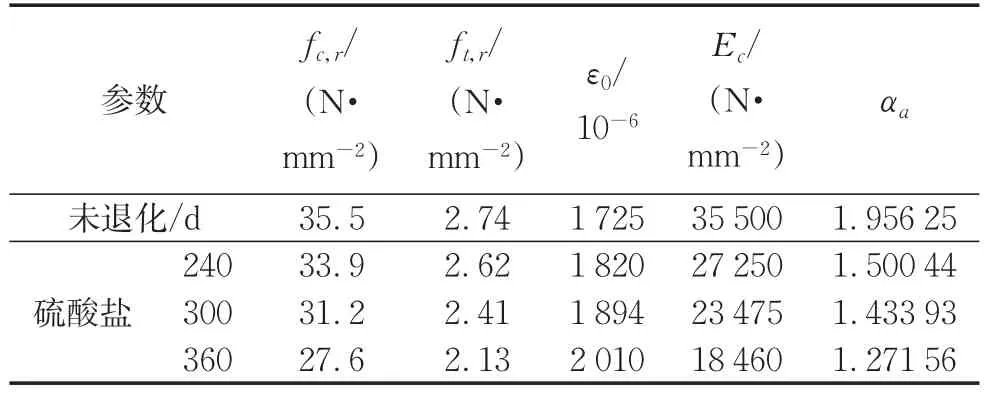
表1 混凝土的主要计算参数Tab.1 Computational parameter table of concrete

（2）螺栓

螺栓采用双折线模型，可分为弹性段、强化段和理想塑性段等三个阶段。其中，弹性段和强化段的弹性模量分别为2.1×105N·mm-2和2.1×104N·mm-2，屈服强度和极限强度则分别为400 N·mm-2和500 N·mm-2。

2.2 影响分析

计算工况如下：①侵蚀时间分别取240d、300d及360d；②侵蚀厚度分别取1cm、2cm及3cm；③轴力分别取500kN、900kN、1 300kN。

（1）侵蚀时间影响

取轴力为1 300kN，硫酸盐侵蚀厚度为3cm作为计算工况，结果见表2和图14～图17。

表2 硫酸盐侵蚀时间对纵缝接头力学性能的影响Tab.2 Affection of sulfate attack time on mechanical property of longitudinal joint

基于表2和图14～图17的数据，总结出如下规律：①混凝土被硫酸盐侵蚀对纵缝接头力学性能的影响主要体现在外表面边缘混凝土接触之后。②随着侵蚀时间延长，纵缝接头极限弯矩不断减少，减幅较为平均，至360d时，最大降低约6%。③纵缝接头各变形量最大值也随侵蚀时间的增长而减小，但减幅有差异。至360d时，内表面张开量减幅约15%，外表面压缩量减幅约9%，转角减幅约13%，而螺栓应变的减幅约18%。

（2）侵蚀厚度影响

图14 不同侵蚀时间接缝内表面张开量与正弯矩的关系Fig.14 Relation between seam opening of inner surface and sagging moment based on different attack time

图15 不同侵蚀时间接缝外表面压缩量与正弯矩的关系Fig.15 Relation between seam compression of outer surface and sagging moment based on different attack time

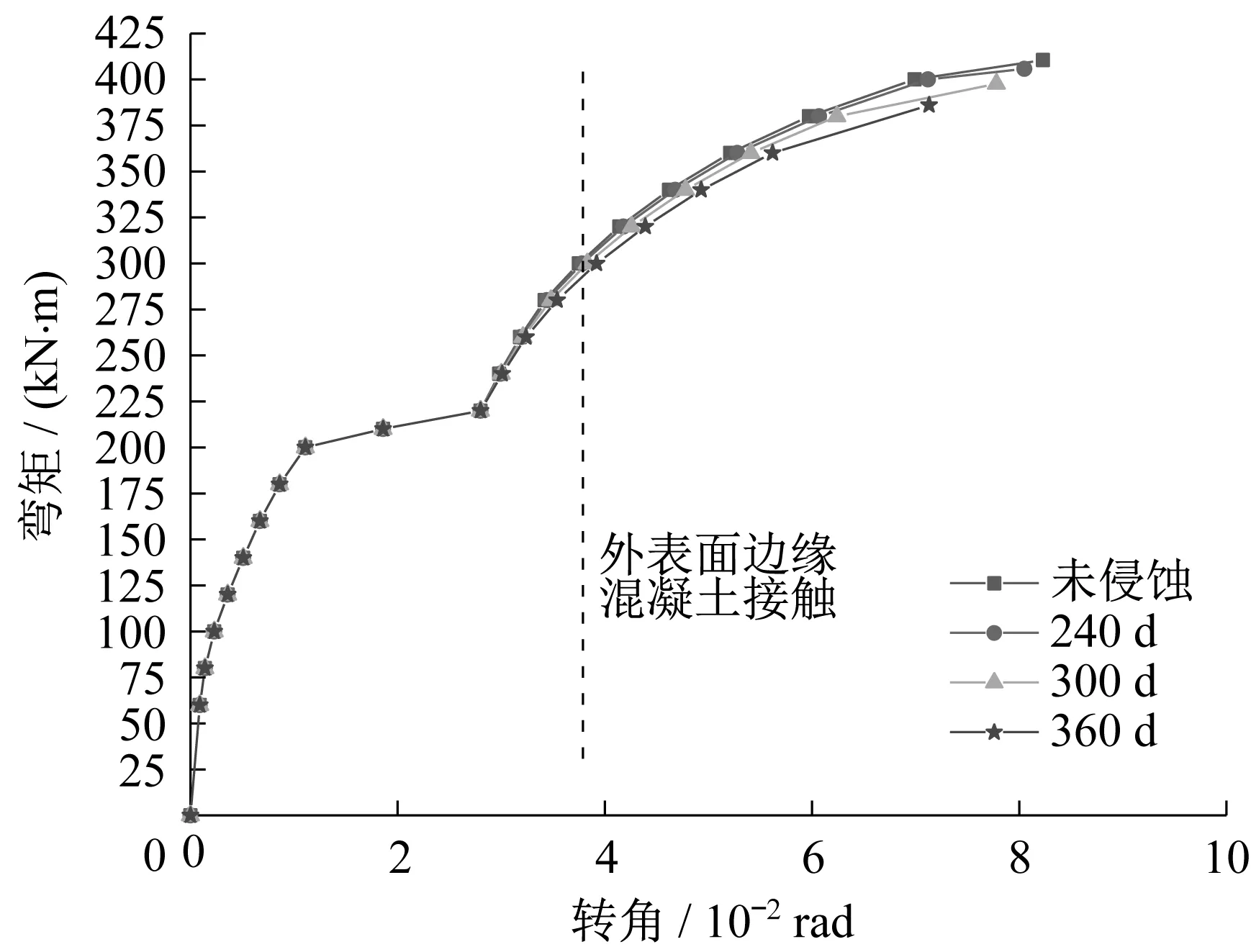
图16 不同侵蚀时间接缝转角与正弯矩的关系Fig.16 Relation between seam rotation angle and sagging moment based on different attack time

图17 不同侵蚀时间螺栓应变与正弯矩的关系Fig.17 Relation between bolt strain and sagging moment based on different attack time

取轴力等于1 300kN，硫酸盐侵蚀时间360d作为计算工况，结果见表3和图18～图21。考虑硫酸盐侵蚀的影响主要在外表面边缘混凝土接触之后，图18～图21中仅列出接触之后的弯矩和变形量。分析图表数据可知，随着侵蚀厚度的增大，纵缝接头极限弯矩及各变形量最大值均不断减少，且减幅不断增大。

表3 硫酸盐侵蚀厚度对纵缝接头力学性能的影响Tab.3 Affection of sulfate attack thickness on mechanical property of longitudinal joint

图18 不同侵蚀厚度接缝内表面张开量与正弯矩的关系Fig.18 Relation between seam opening of inner surface and sagging moment based on different attack thickness

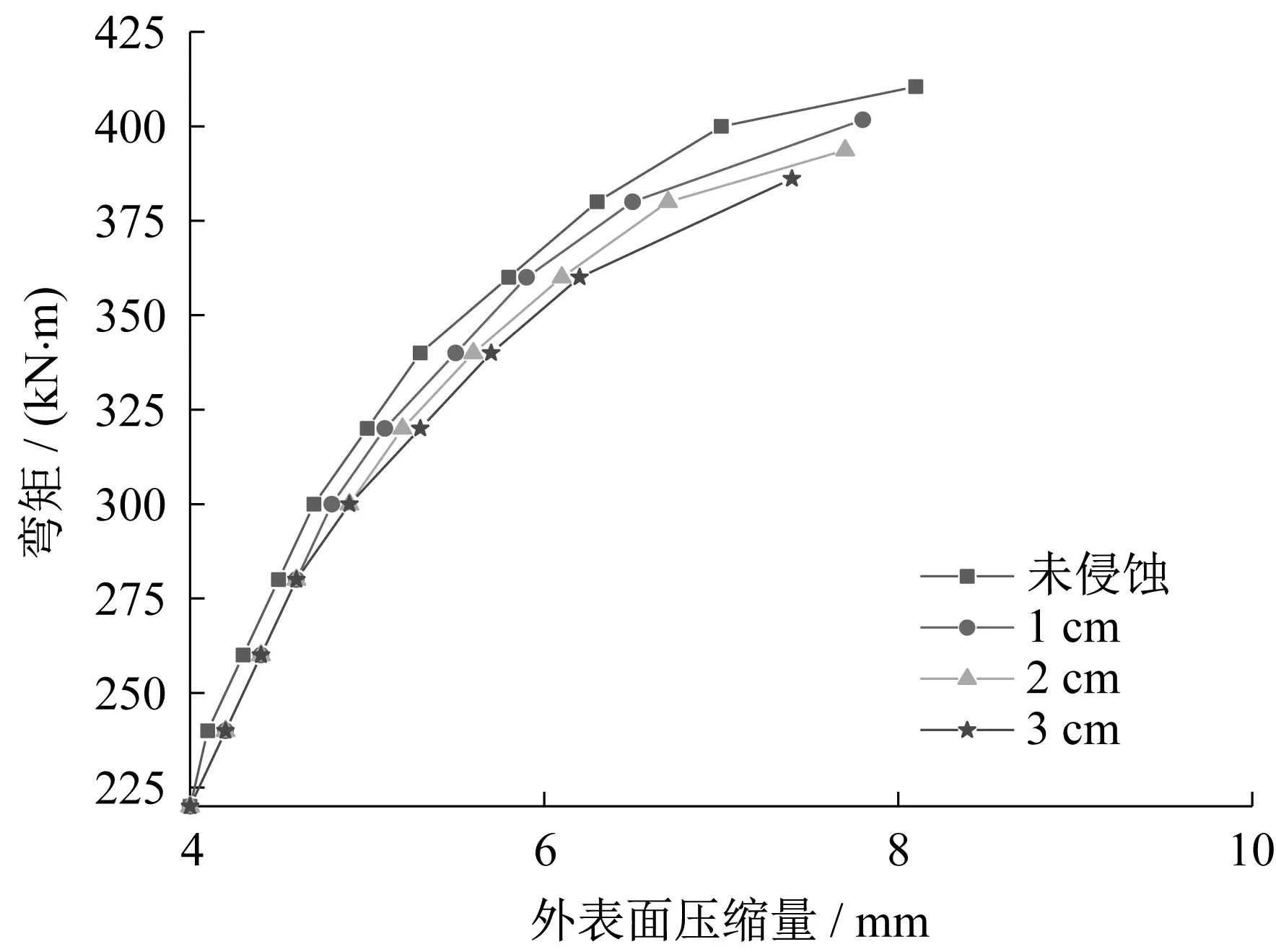
图19 不同侵蚀厚度接缝外表面压缩量与正弯矩的关系Fig.19 Relation between seam compression of outer surface and sagging moment based on different attack thickness

图20 不同侵蚀厚度接缝转角与正弯矩的关系Fig.20 Relation between seam rotation angle and sagging moment based on different attack thickness

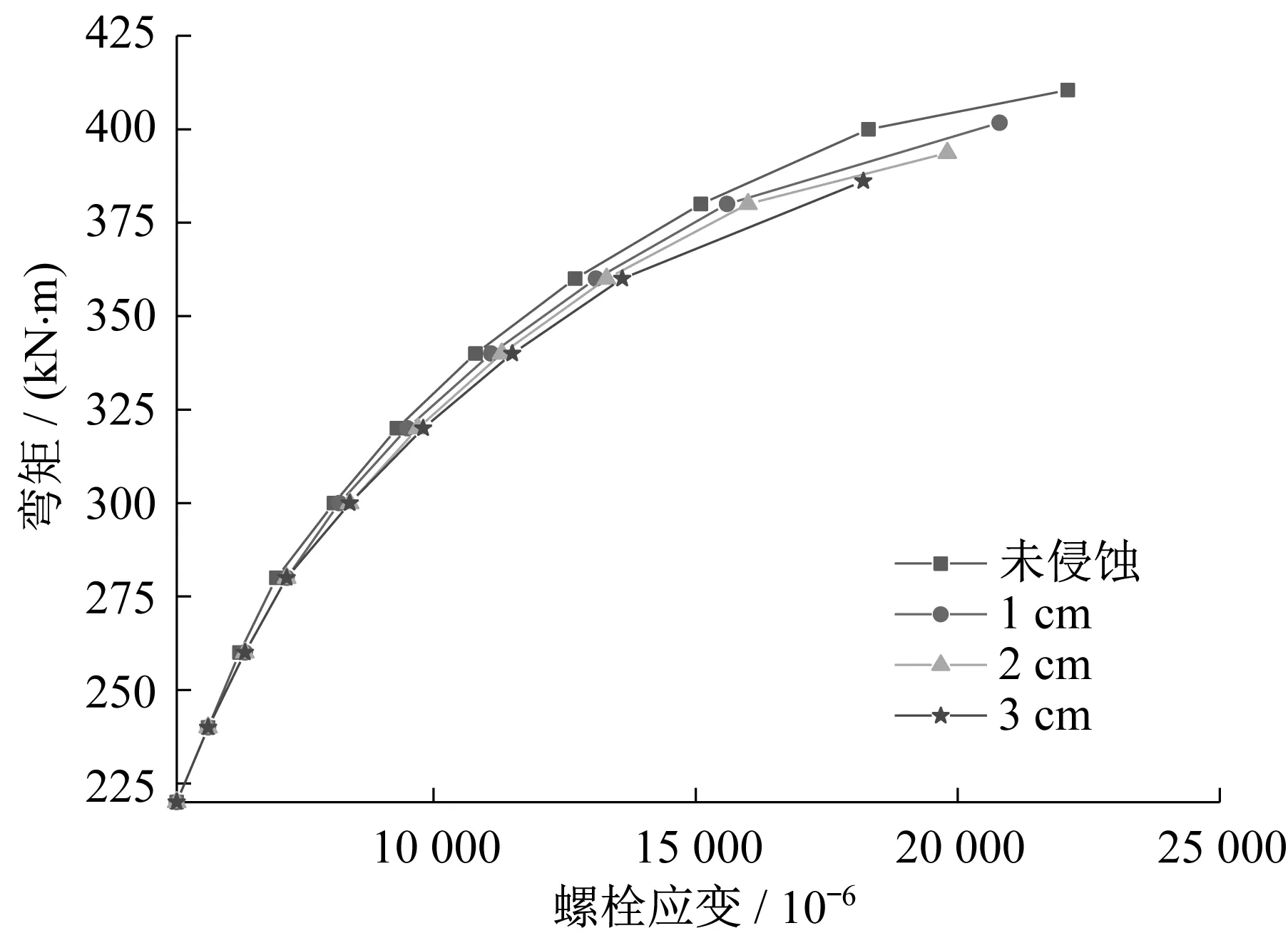
图21 不同侵蚀厚度螺栓应变与正弯矩的关系Fig.21 Relation between bolt strain and sagging moment based on different attack thickness

3 数值计算验证

3.1 材料本构关系

混凝土和螺栓本构关系参数设置参照2.1节。钢筋分为主筋和箍筋，主筋屈服强度500MPa，箍筋屈服强度400MPa，钢筋的本构关系采用理想弹塑性模型（双折线）。橡胶弹性密封垫设为不可压缩材料，考虑材料及几何非线性，采用Mooney-Rivlin二参数模型。

3.2 网格划分、约束及边界条件

钢筋单元及非线性弹簧单元如图22所示，整体网格划分情况如图23所示。纵缝接头各部件之间均为面-面接触，弹性密封垫和管片混凝土之间及螺栓与手孔之间均设定为绑定接触，其他均设定为标准接触。钢筋与管片混凝土的约束关系为“嵌入”，即认为钢筋在混凝土中不发生滑移现象。边界条件如图24所示，荷载加载时，一端固定铰支，另一端为水平自由铰支。通过施加初始预应力的方法对螺栓加载预紧力，取值为100kN。

图22 钢筋单元及弹簧单元模型Fig.22 model of reinforcement element and spring element

图23 纵缝接头整体网格划分图Fig.23 generalmesh generation oflongitudinal joint

3.3 对比分析

由图25可知，力学模型与数值计算所得内表面张开量与正弯矩关系曲线趋势基本一致，均可划分为6个特征点及7个阶段。其中，力学模型结果中c阶段在d阶段之后，而数值计算结果则刚好相反。力学模型所得关系曲线在b阶段以后相对数值计算整体上抬。除c阶段的弯矩、d阶段的内表面张开量以及f阶段的弯矩之外，两种方式所得各个特征点所对应的弯矩值和内表面张开量数据差异不大。图26及图27表示数值计算结果，从中可看出，随着侵蚀时间和厚度增长，接头极限弯矩和变形量值均增大，与力学模型所得结果相同。

图24 数值模型边界条件（单位：mm）Fig.24 Boundarycondition ofnumericalmodel(unit:mm)

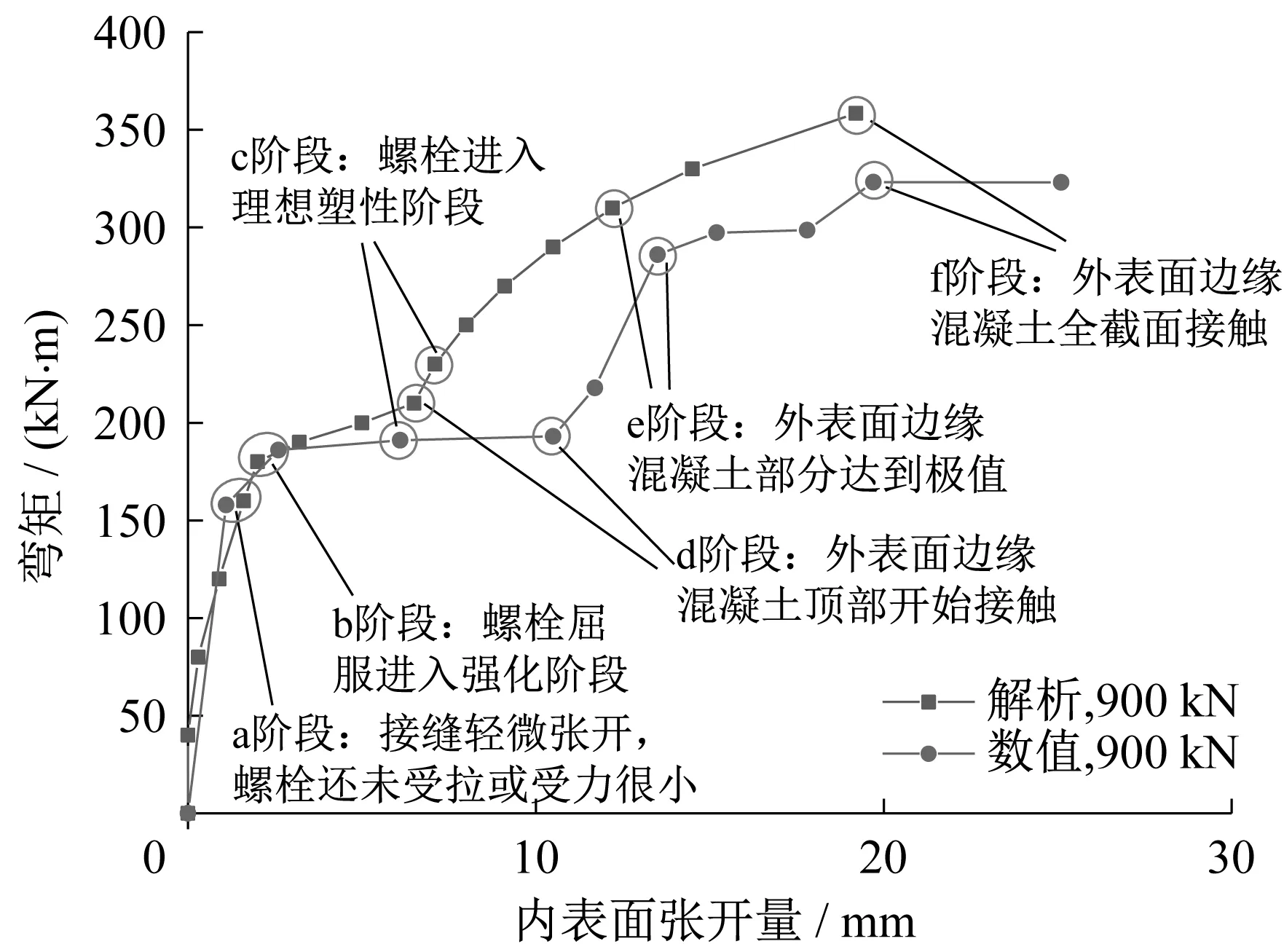
图25 力学模型与数值计算结果对比分析Fig.25 Result comparison and analysis of the mechanical and numerical model

图26 不同侵蚀时间内表面张开量与正弯矩关系（数值）Fig.26 Relation between seam opening of inner surface and sagging moment based on different attack time(numerical model)

图27 不同侵蚀厚度内表面张开量与正弯矩关系（数值）Fig.27 Relation between seam opening of inner surface and sagging moment based on different attack thickness(numerical model)

4 结论

采用力学模型及数值模拟分析混凝土被硫酸盐侵蚀后的地铁盾构隧道纵缝接头力学性能，主要结论有：

（1）建立了能够考虑接缝细部构造、表面混凝土及螺栓等且接缝截面可离散为不同类型受压区的纵缝接头正弯矩力学模型。采用全积分形式进行混凝土本构关系运算，适用研究混凝土被硫酸盐侵蚀对纵缝接头力学性能的影响。

（2）理论解析与数值计算所得接缝张开量与弯矩的关系曲线趋势基本一致。正弯矩作用下，两种方式所得关系曲线均可分为6个特征点和7个阶段，主要特征点弯矩和变形值差异不大。

（3）随着硫酸盐侵蚀时间的增长，纵缝接头极限弯矩不断减少，但减幅较为平均。同时，各变形量最大值也随着侵蚀时间的增长而减小，但减幅各自不同。随着硫酸盐侵蚀厚度的增大，纵缝接头极限弯矩及各变形量最大值均不断减少，且减幅不断增大。