基于列车电机械制动系统夹紧力的控制算法优化

吴萌岭，雷 驰，陈茂林

（1.同济大学 铁道与城市轨道交通研究院，上海201804；2.同济大学 机械与能源工程学院，上海201804）

列车电机械制动系统（EMB）于本世纪初试用于日本鹿儿岛有轨电车，在我国是一种新型的制动系统。有别于常见的空气或液压制动系统，其以电机作为动力源，实现列车制动功能。具有结构简单、响应快、精度高等特点［1］。EMB属于机电一体化的伺服系统，由于机械传动过程中普遍存在传动误差，系统的输出精度受影响，精确控制夹紧力成为EMB应用的重要因素。

文献［2］中，通过分析电机、行星齿轮和螺纹的摩擦效应，建立了摩擦仿真模型，并提出了夹紧力的估算方法。文献［3］考虑了系统的黏性摩擦和参数不确定等非线性因素，设计了夹紧力控制器。文献［4］的研究表明在制动器饱和、载荷相关摩擦以及非线性刚度作用下，EMB的性能将受到很多限制。文献［5］建立了EMB系统模型，采用PI控制实现了电流环、速度环、压力环的级联闭环控制，并通过仿真进行了验证。文献［6］设计了一种基于模糊控制的智能执行器逻辑，并通过仿真验证了该逻辑的正确性。上述研究中控制算法对系统模型精确度要求较高，参数辨识过程复杂，且只完成了仿真分析，未进行试验研究。本文针对EMB系统，研究了其开环特性，设计了不依赖于模型的闭环夹紧力优化算法，最终，通过硬件在环试验，验证了算法的有效性。

1 电机械制动系统作用原理

在同济大学制动技术研究所，针对精确控制电机驱动的制动系统，电机械制动系统的研究已基本成型，一系列的电机械制动装置样机也已研制完成。图1即为电机械制动装置样机实物图。

图1 电机械制动装置Fig.1 Electro-mechanical braking device

该电机械制动装置主要由电机、编码器、机械传动部件和力传感器组成，如图2所示。

图2 电机械制动装置原理Fig.2 Schematic diagram of electro-mechanical braking device

其中电机为三相永磁同步电机（PMSM），其控制基于编码器测得的电机位置信号进行，采用空间矢量控制［7］。在id=0控制策略下，电机输入指令可简单看作电流信号i*q，并且其输出转矩Te与实际电流iq理论上是成正比的。其比值可用A1，表达式为

机械传动部件用于将电机的输出转矩转换成推力，其理论传动倍率用A2表示。则电机械制动装置的输出夹紧力Fc和电流iq理论比值为

所以理论上，想要使电机械制动装置产生大小为的夹紧力，那么只要令电机输入电流大小为

力传感器的作用是检测实际夹紧力Fc大小。

2 硬件在环试验环境搭建

为了对电机械制动装置特性进行研究，搭建硬件在环试验平台如图3所示。该平台由工控机、电机驱动板、信号调理模块、电机械制动装置和电源模块等组成。

图3 硬件在环试验台Fig.3 Hardware-in-loop test bench

工控机选用美国国家仪器NI（NATIONAL INSTRUMENTS）公司的PXI系统，其配备数据采集卡PXI-6221和CAN-Open通讯卡PXI-8531，主要用于实时计算目标电流i*q，并基于CAN-Open总线协议，将目标电流发送给电机控制板；电机控制板基于空间矢量算法，精确控制电机电流iq；电机械制动装置在电机的驱动下，产生夹紧力Fc，并通过传感器反馈给工控机；信号调理模块用于处理传感器与工控机数据采集卡之间的信号匹配问题；电源模块用于给整个系统供电。

3 开环特性研究

从控制的角度讲，A1A2为系统的开环增益，为确定其值，需对系统进行开环响应试验。

将电机的目标电流参数值设置成：从0A开始，每过1s电流值阶跃上升1A，上升到9A后；每过1s又下降1A，直到下降到0A为止。在这个过程中，测试夹紧力的变化，并记录数据，之后重复试验两次。夹紧力三次试验的变化曲线如图4所示。

试验结果表明，在三次相同目标电流参数的工况下，所产生的夹紧力存在较大误差，且误差在大电流值下更为突出，这说明电机械制动装置开环控制下夹紧力输出性能不稳定，从数学角度来说，A1A2的值是时变的。

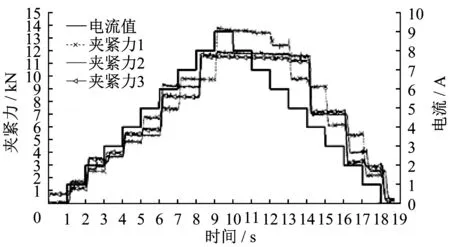
图4 开环阶段阶跃响应曲线Fig.4 Step-stage response curve on open loop

进一步地试验，将上位机的目标电流参数值设置为连续变化（从0A上升至9A，再下降至0A），夹紧力变化曲线如图5所示。

图5中，电机电流参数是连续变化的，但夹紧力输出却是跳变的。另外相比上升过程，夹紧力下降过程中更难跟随电流参数变化而变化，即夹紧力施加后较难缓解。从数学角度来说，A1A2是具有非线性特征的。

事实上，电机由于转子阻尼作用、磁势高次谐波、定子/转子铁芯磁链饱和以及磁滞等产生损耗；而机械传动部件也存在加工与装配误差、非线性摩擦阻力等影响。正是这些因素，使A1A2表现出时变非线性的特征。

对系统开环特性的研究表明：通过开环控制电机电流无法满足对夹紧力的精确控制要求。

图5 开环斜坡响应曲线Fig.5 Slope response curve on open loop

4 闭环控制算法研究

4.1 PID控制分析

PID控制是控制理论中运用广泛的一种控制方法，其具有易懂、通用、简单等特点［8］。但由于带噪声的夹紧力信号较难获得良好的微分信号，所以考虑在PID控制上去除微分项，即是PI控制。

其表达式为

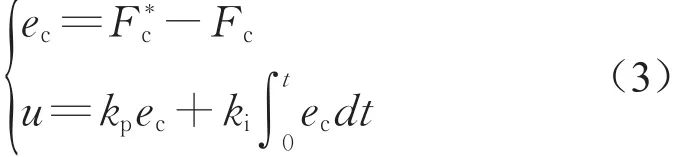
式中：ec为夹紧力目标值与实际值的差，kpec为比例项，其中kp为比例系数为积分项，其中ki为积分系数。

PI控制中，运用比例项误差进行调节，理论上只要kp，A1，A2三者乘积足够大，系统稳态误差将很小；运用积分项误差的累积消除系统稳态误差。

基于硬件在环试验条件下，对PI控制进行测试。设置目标夹紧力阶跃上升与下降。根据记录的夹紧力数据，得出夹紧力PI控制过程中变化曲线，如图6所示。

图6中，夹紧力上升过程响应时间tr（上升到目标夹紧力的90%，下同）为0.15s，超调量Mp（最大峰值与稳态值的差的绝对值，下同）为0.76kN；夹紧力下降过程响应时间为0.13s，超调量为1.93kN。为模拟更多制动工况，设置目标夹紧力阶段阶跃上升与下降，得出实测夹紧力变化曲线，如图7所示.

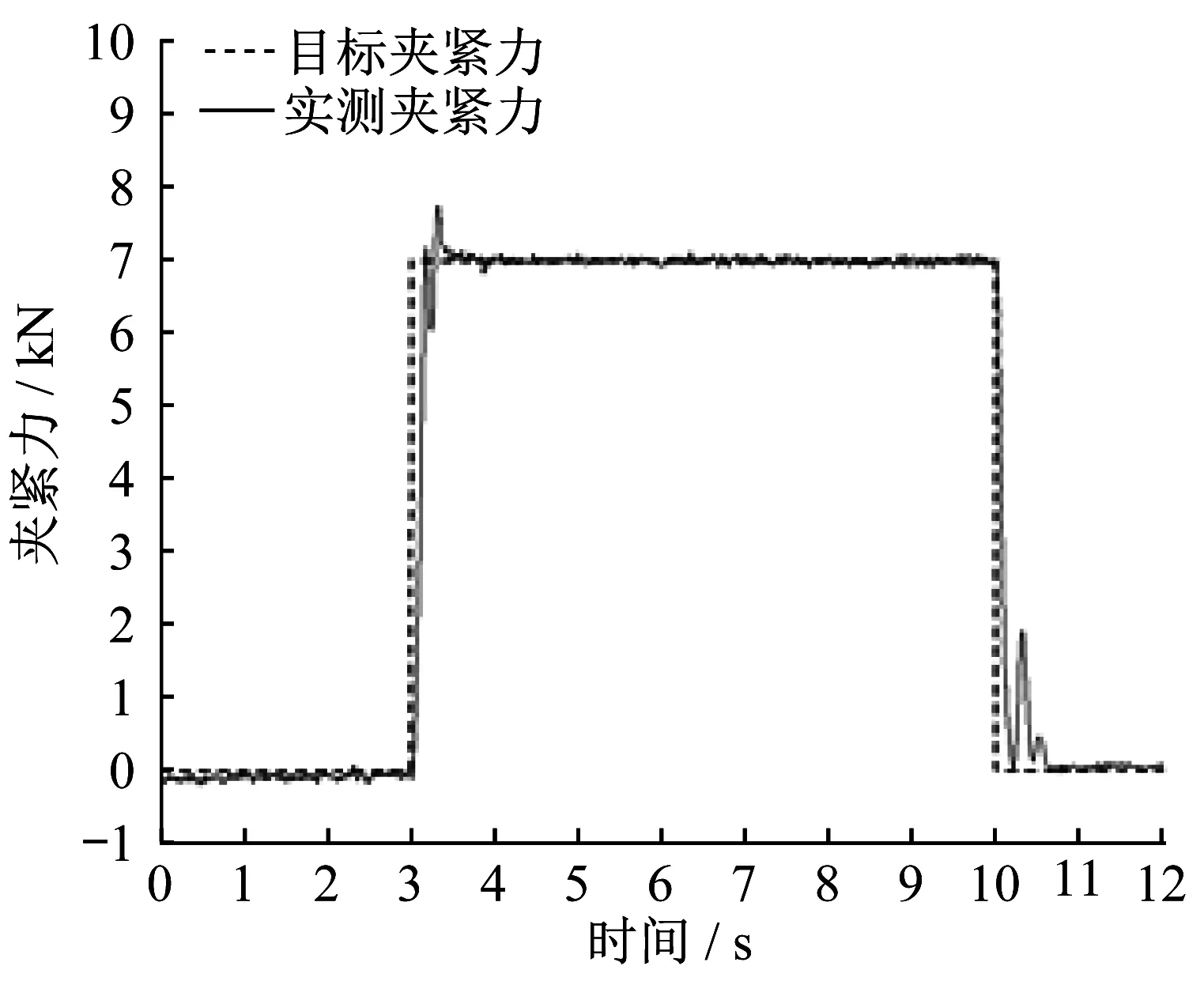
图6 PI控制阶跃响应曲线Fig.6 Step response curve on PI

计算夹紧力上升和下降阶的段阶跃响应的间和超调量，如表1、2所示。

由图6、7可以看出，在闭环控制下，电机械制动装置的输出夹紧力稳态响应达到了较高的精度，但其瞬态响应还存在些问题——夹紧力在调节过程中超调量偏大。

4.2 优化控制算法（OA）分析

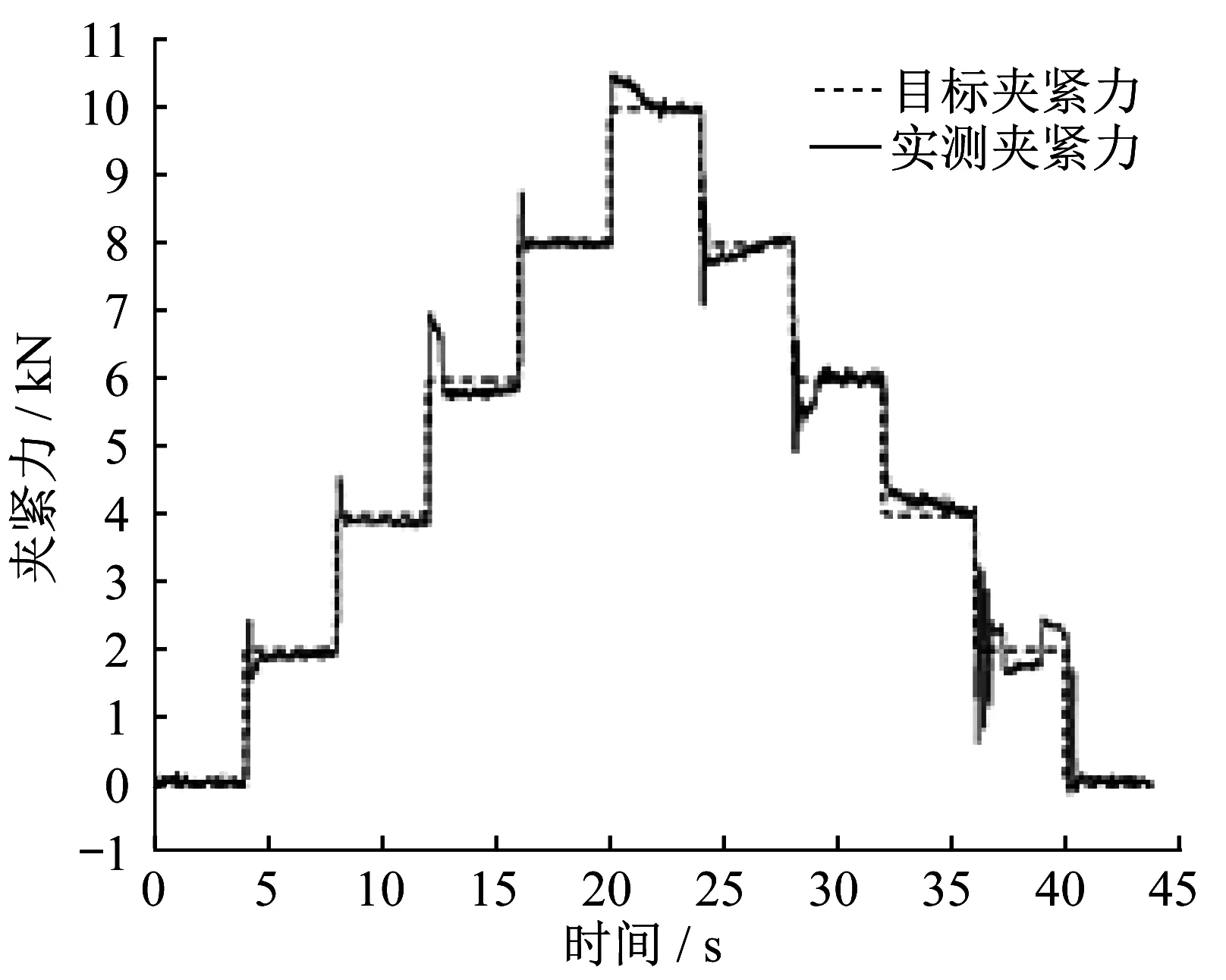
图7 PI控制阶段阶跃响应曲线Fig.7 Step-stage response curve on PI

表1 PI控制下阶段上升的瞬态性能指标Tab.1 Transient performance index of rising stage on PI

表2 PI控制下阶段下降的瞬态性能指标Tab.2 Transient performance index of phase decline on PI

由上节可知，夹紧力PI控制存在的问题是产生超调，而完整的PID控制中微分项可以减少、甚至消除系统超调。然而，对于实际存在的噪声信号，很难获得优质的微分信号，因为微分会放大噪声［8］。为解决这个问题，引入跟踪微分器提取夹紧力的微分信号［9］。其输入是带噪声的夹紧力信号Fc，输出为夹紧力的微分F˙c，如下：

式中：fhan()函数为离散系统最速控制综合函数，其表达式如下：

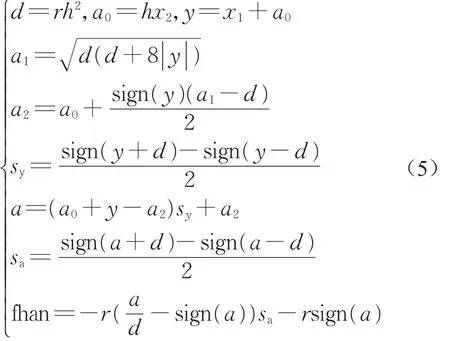
另外，在目标夹紧力输入中增加一个缓冲过程，也可以适当减小系统响应的超调。为防止缓冲后的输出不抖动、不超调，设计一阶惯性环节作为缓冲过程，其输入是目标夹紧力F*c(k)，输出是缓冲后的目标夹紧力F⌒*c(k)和目标夹紧力微分F˙*c(k)，如下所示。

结合增加微分项和缓冲过程，得到了优化后的夹紧力控制方案，如图8所示。

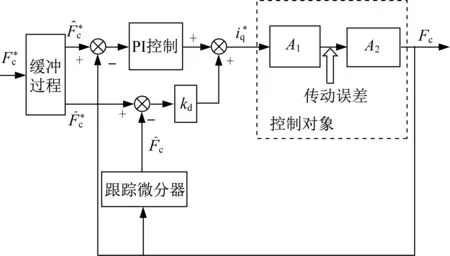
图8 夹紧力优化算法（OA）框图Fig.8 Block diagram of clamping force optimized algorithm（OA）

基于硬件在环试验条件下，对优化算法进行测试。设置目标夹紧力阶跃上升与下降。根据记录的夹紧力数据，得出夹紧力OA控制过程中变化曲线，如图9所示。

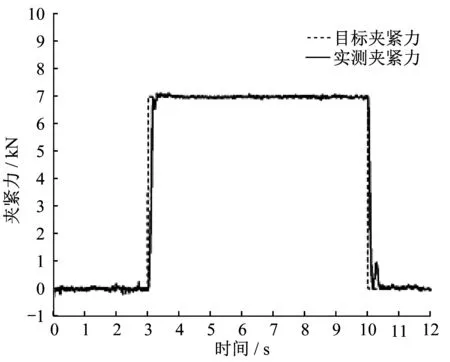
图9 OA控制阶跃响应曲线Fig.9 Step response curve on OA

图9 中，夹紧力上升过程响应时间tr为0.14s，超调量Mp为0kN；夹紧力下降过程响应时间为0.12s，超调量为0.93kN。为模拟更多制动工况，设置目标夹紧力分段阶跃上升与下降，得出实测夹紧力变化曲线，如图10所示。

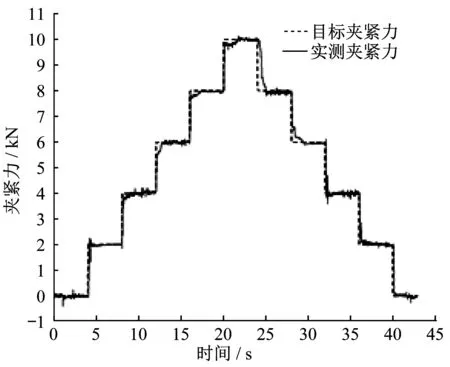
图10 OA控制阶段阶跃响应曲线Fig.10 Step-stage response curve on OA

计算夹紧力上升和下降阶的段阶跃响应的间和超调量，如表3、4所示。

与经典PID控制相比，OA控制基本消除了夹紧力阶跃响应的超调，提高了电机械制动装置的输出性能。在其控制下，夹紧力阶跃响应时间大多落在0.1～0.2s范围内，控制精度基本在0.05kN范围内。

表3 OA控制下阶段上升的瞬态性能指标Tab.3 Transient performance index of rising stage on OA

表4 OA控制下阶段下降的瞬态性能指标Tab.4 Transient performance index of phase decline on OA

4.3 优化算法频域分析

实际轨道交通列车制动时，制动力不是线性的阶段上升或者阶段下降，而是会随着速度变化而变化。为此，采用电机械制动装置进行夹紧力的跟踪响应试验，验证算法的合理性。目标夹紧力分别设置为1/6Hz、0.3Hz、0.6Hz和1.2Hz的正弦波信号，实测夹紧力曲线如图11所示。

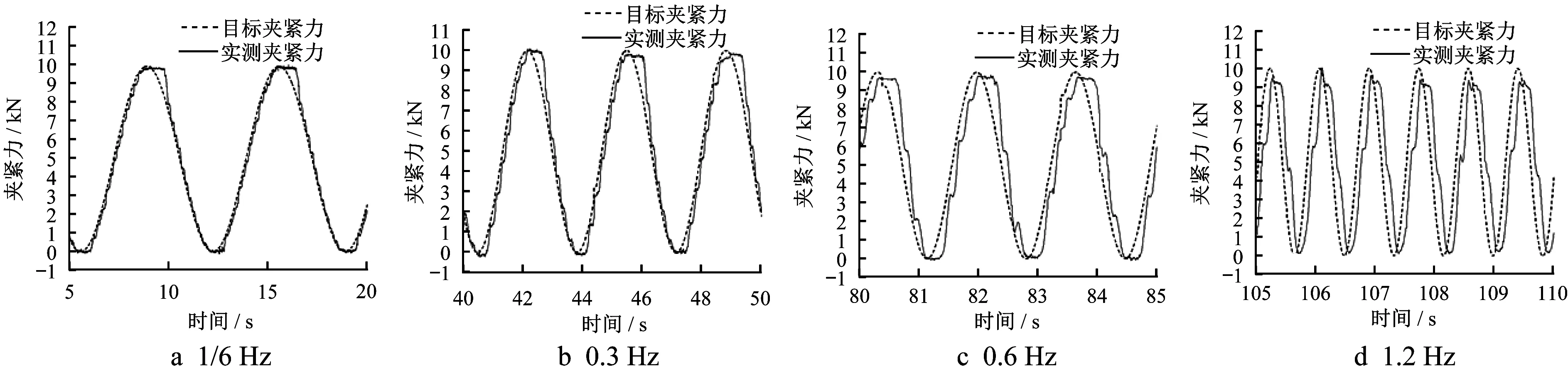
图11 频率响应曲线Fig.11 Frequency response curves

从图11曲线变化来看，相对目标值，实测夹紧力在4个跟随频率下幅值没有明显下降，有一定的相位延迟。另外，可以看到，夹紧力在最小值的上升处和最大值的下降处都有明显的滞后，并且最大值下降处滞后更明显。

根据四种频率下夹紧力正弦响应曲线，作出电机械制动装置夹紧力的频响特性曲线，如图12所示。

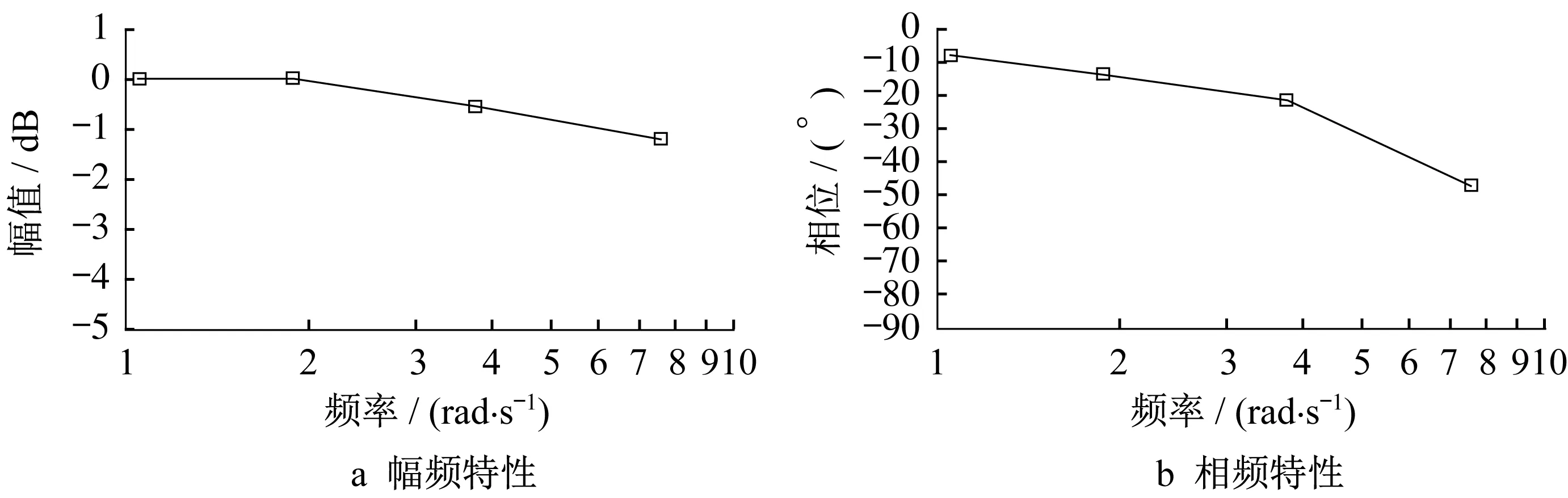
图12 电机械制动系统频响特性曲线（伯德图）Fig.12 Frequency response characteristic curve of elctro-mechanical brake system（Bode）

由图12可知，电机械制动系统频率从0增加到7.5 rad·s-1过程中，夹紧力幅值略有下降、但不明显，相位略有延迟。图13为某电控空气制动系统制动缸压力控制的频率特性［10］。频率从0rad·s-1增加到7.5 rad·s-1过程中，该电控空气制动系统制动缸压力幅值下降明显，相位延迟近180°。

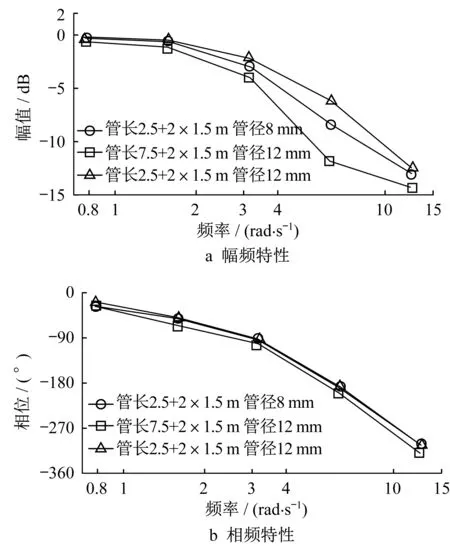
图13 某电控空气制动系统频响特性曲线（伯德图）Fig.13 Frequency response characteristic curve of one elctro-pneumatic brake system（Bode）

由此可以得到结论：电机械制动装置夹紧力控制的频率特性要远好于电控空气制动系统制动缸压力的频率特性。

5 结语

通过对电机械制动系统开环特性的研究，分析了引起系统时变非线性的因素，指出在开环下系统夹紧力难以控制。随后，在经典PID控制的基础上，引入跟踪微分器和缓冲过程，设计了针对夹紧力的优化控制算法。并通过硬件在环试验对比验证了优化算法的合理性——优化算法基本消除了控制超调，有效改善了瞬态响应，提高了系统输出性能。最后，在频域上对比分析了电机械制动系统与某一电控空气制动系统，说明了电机械制动系统的优越性。