一种实现截止频率变换的数字滤波器*
陈绍荣,张振宇,朱行涛,徐 舜
(陆军工程大学通信士官学校,重庆 400035)
0 引言
从广义上讲,数字信号处理的过程,就是数字信号滤波的过程,因此,数字滤波器的设计就成为关键问题。数字滤波器分为两类[1-2],一是无限冲激响应(IIR)数字滤波器,二是有限冲激响应(FIR)数字滤波器。目前IIR 数字滤波器设计最通用的方法是借助于模拟滤波器的设计方法,即首先按要求设计相应的模拟滤波器,再利用时域模仿的方法或双线性变换来设计数字滤波器,其中,时域模仿的方法有两种,一是单位冲激响应不变法,二是单位阶跃响应不变法。模拟滤波器的设计已有一套相当成熟的方法,它不仅有一套完整的设计公式,而且还有较完整的图表供查询。充分利用这些已有的资源,将会给IIR 数字滤波器设计带来很大的方便;FIR 数字滤波器设计方法有窗函数法,频率抽样设计法和切比雪夫逼近法。本文基于著作[3-4],揭示了插值、抽取及重排序列的z变换与频谱之间相互计算的方法;提出了一种数字滤波器前置插值器和后置重排器的级联结构,从时域和频域分析了该结构实现数字滤波器截止频率变换的原理,并给出了利用该结构来实现数字带通滤波器的截止频率变换,通过数字信号的滤波来选择所需数字信号的实例。
1 序列的插值、抽取及重排
设周期为N的周期冲激序列为:
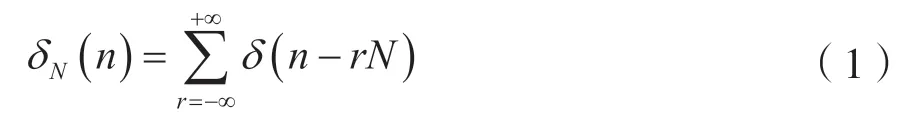
式中,N为正整数。
1.1 插值序列
利用周期冲激序列δN(n),可以定义插值序列。一个序列f(n)的插值序列y(n)定义为:

式(2)表明,插值序列y(n)是在序列f(n)中相邻两位之间插入N-1 个零值位的结果。
1.2 抽取序列
利用周期冲激序列δN(n),可以定义抽取序列。一个序列f(n)的抽取序列y(n)定义为:

式(3)表明,抽取序列y(n)是抽取出序列f(n)中n=rN(r=0,±1,±2,…)位的结果。
1.3 重排序列
若N为正整数,则一个序列f(n)的重排序列y(n)定义为:

式(4)表明,重排序列y(n)是抽取出序列f(r)中的r=Nn位,再按序号n依次重新排列的结果。
2 插值、抽取及重排序列的z 变换
下面介绍插值序列、抽取序列及重排序列的z变换。
2.1 插值序列的z 变换
若ZT[f(n)]=F(z),Ra<|z|<Rb,则有:
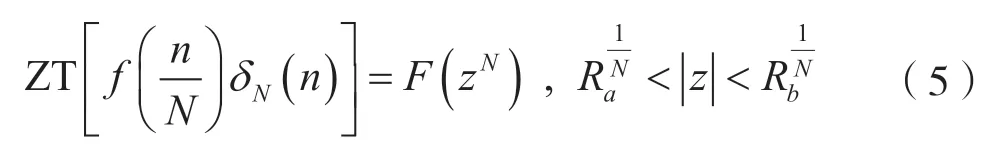
证明:由双边ZT 的定义,可得:
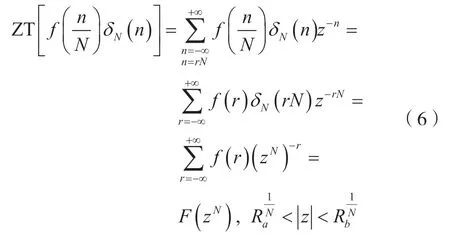
由式(6)可知,式(5)成立。
2.2 抽取序列的z 变换
若ZT[f(n)]=F(z),Ra<|z|<Rb,则有:

证明:由于:

由双边ZT 的定义,并注意到式(8),则有:
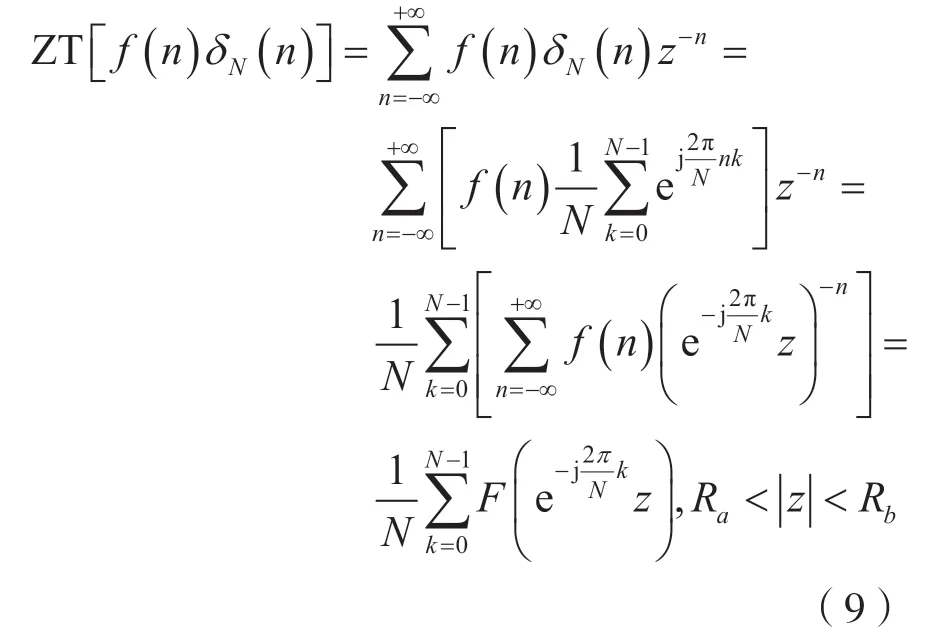
由式(9)可知,式(7)成立。
2.3 重排序列的z 变换
若ZT[f(n)]=F(z),Ra<|z|<Rb,则有:

证明:由双边ZT 的定义,并注意到式(8),则有:
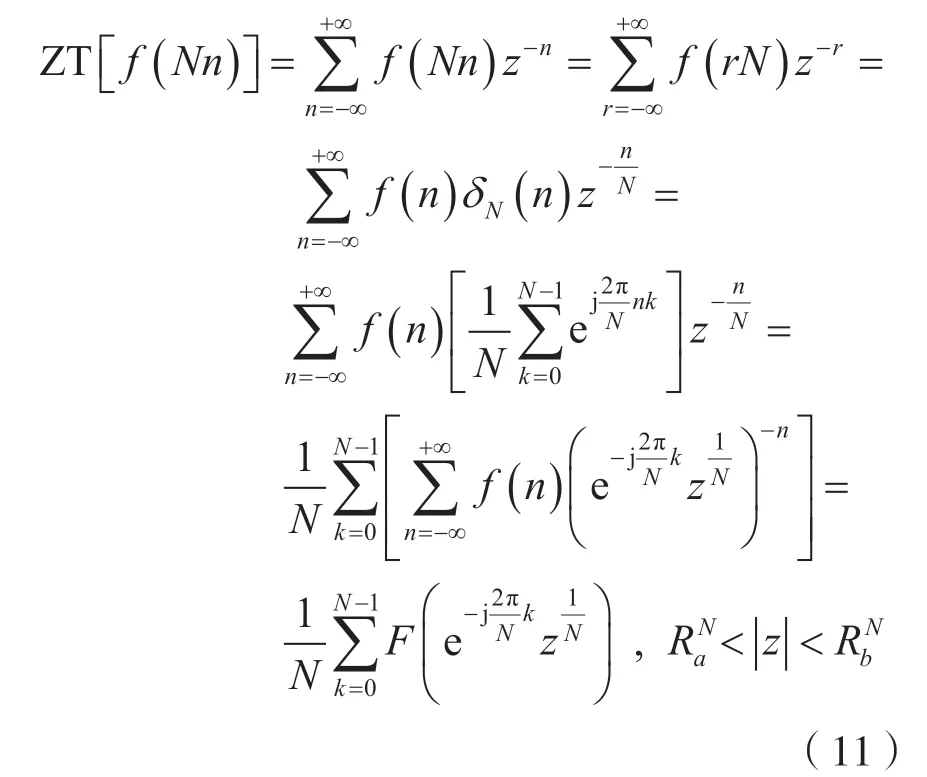
由式(11)可知,式(10)成立。
3 插值、抽取及重排序列的频谱
序列f(n)的频谱,即DTFT,就是单位圆周上的z变换,若序列f(n)的频谱不存在,可以证明其插值序列、抽取序列及重排序列的频谱也不存在。因此,研究f(n)的插值序列、抽取序列及重排序列的频谱,意味着序列f(n)自身的频谱F(ejω)存在,即序列f(n)的z变换F(z)的收敛域包含z平面上的单位圆周,并且,序列f(n)的频谱F(ejω)可利用其z变换F(z)进行计算,即:

3.1 插值序列的频谱
若DTFT[f(n)]=F(ejω),则有:
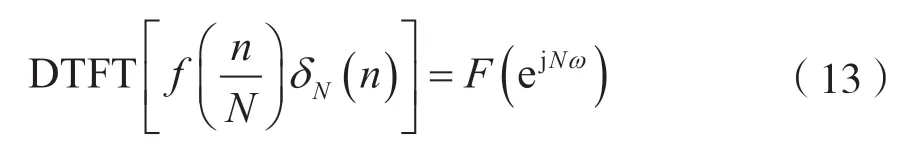
证明:
因为序列f(n)的z变换F(z)的收敛域包含z平面上的单位圆周,即满足Ra<1<Rb,由式(5)可知,插值序列的z变换F(zN)的收敛域为,并且满足,即其z变换F(zN)的收敛域也包含z平面上的单位圆周,于是,有:
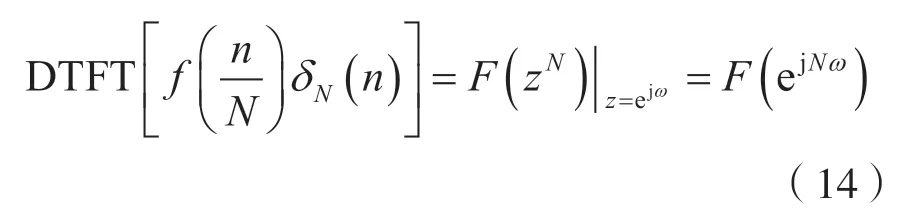
由式(14)可知,式(13)成立。
3.2 抽取序列的频谱
若DTFT[f(n)]=F(ejω),则有:

证明:
因为序列f(n)的z变换F(z)的收敛域包含z 平面上的单位圆周,即满足Ra<1<Rb,由式(7)可知,抽取序列f(n)δN(n)的z变换的收敛域为Ra<|z|<Rb,并且满足Ra<1<Rb,即的收敛域也包含z平面上的单位圆周,于是,有:

由式(16)可知,式(15)成立。
3.3 重排序列的频谱
若DTFT[f(n)]=F(ejω),则有:
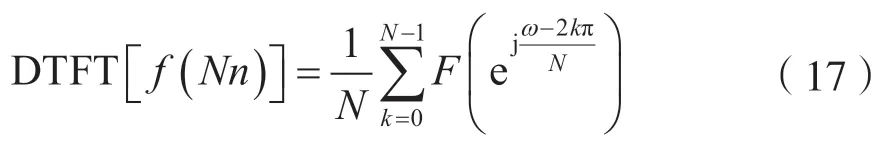
证明:
因为序列f(n)的z变换F(z)的收敛域包含z平面上的单位圆周,即满足Ra<1<Rb,由式(10)可知,重排序列f(Nn)的z变换的收敛域为,并且满足,即的收敛域也包含z平面上的单位圆,于是,有:
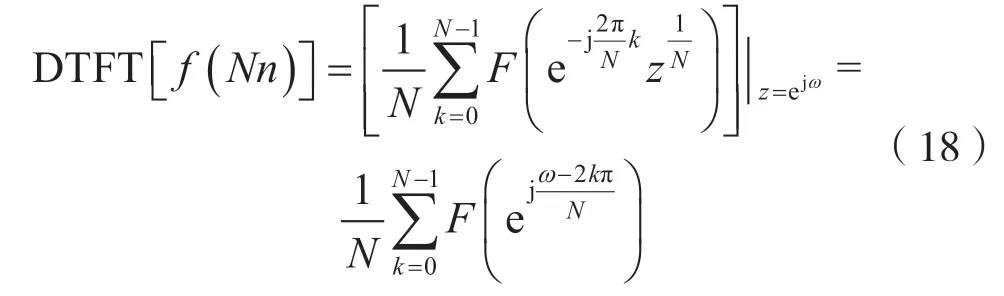
由式(18)可知,式(17)成立。
若插值序列的频谱在z平面上的单位圆周上解析,则其z变换可利用其频谱进行计算,即:
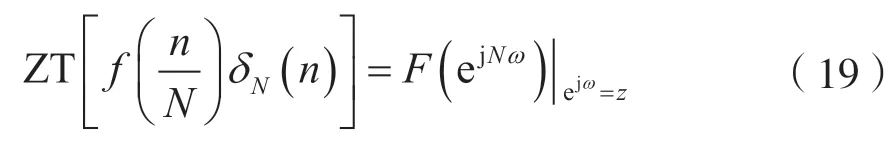
若抽取序列的频谱在z平面上的单位圆周上解析,则其z变换可利用其频谱进行计算,即:
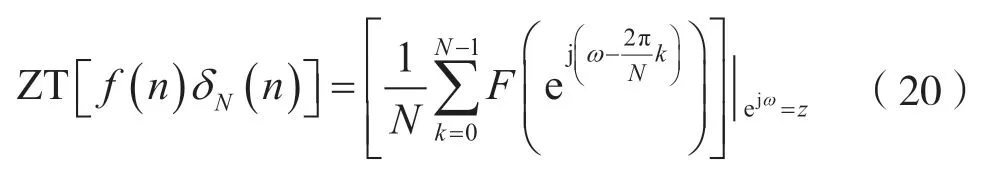
若重排序列的频谱在z平面上的单位圆周上解析,则其z变换可利用其频谱进行计算,即:

例1:设理想数字低通滤波器的单位冲激响应为h1(n),其频率特性为:

式中,G2ωc(ω)=ε(ω+ωc)-ε(ω-ωc),ε(ω)为单位阶跃函数,ωc为截止角频率,并且0<ωc<π。现对h1(n)做插值,得到,试证明单位冲激响应为h(n)的数字滤波器是数字带阻滤波器。
证明:考虑到:

对式(23)两边取DTFT,并注意到式(13),则有:

考虑到式(22),并注意到线性卷积的标尺性质及单位冲激函数的标尺性质,则式(24)可写成
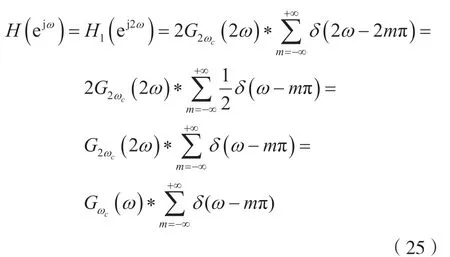
式(25)表明,频率特性H(ejω)是宽度为ωc的单位对称门函数Gωc(ω)按周期π延拓而得的结果。因此,在区间[0,π]上,频率特性H(ejω)的零值区间为[ωc/2,π-ωc/2]。由于单位冲激响应为h(n)的数字滤波器的频率特性H(ejω)在区间[0,π]上的零值区间为[ωc/2,π-ωc/2],因此,该数字滤波器是数字带阻滤波器。
4 实现截止频率变换的数字滤波器
插值器和重排器在数字信号处理领域得到了广泛的应用,一种数字滤波器前置插值器和后置重排器的级联结构,如图1 所示。其中,插值器的输出与输入的关系为,数字滤波器的单位冲激响应为h1(n),重排器的输出与输入的关系为y(n)=f2(Nn)。

图1 实现截止频率变换的数字滤波器
4.1 时域分析

考虑到y(n)=f2(Nn),则有:

由式(27)可知,图1 所示的数字滤波器的单位冲激响应为:

式(28)表明,h(n)是抽取出序列h1(r)中的r=Nn位,再按序号n依次重新排列的结果。也就是说,在时域上,通过对单位冲激响应为h1(n)的数字滤波器进行重排,实现了截止频率的变换,得到了单位冲激响应为h(n)的数字滤波器。
4.2 频域分析
考虑到:

对式(29)两边取DTFT,并注意到式(13),可得:

考虑到:

对式(31)两边取DTFT,并注意到式(30)可得:
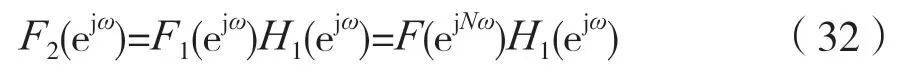
考虑到:

对式(33)两边取DTFT,并注意到式(17)及式(32),可得:

考虑到系统频率特性的定义,由式(34)可得:

对式(35)两边取IDTFT,并注意到式(17),则可以得到与式(28)相同的结果,即:

考虑到式(35),则有:

式(37)表明,H(ejω)仍然是周期为2π的周期函数。H(ejω) 在一周期2π内的频谱是由N个叠加再除以N构成的。也就是说,在频域上,通过对频率特性为H1(ejω)数字滤波器,首先作N的扩展,然后将ω轴上每隔2π的N个频移叠加,这两种运算的结果,实现了截止频率的变换,最后再除以N,就得到了频率特性为H(ejω)的数字滤波器。
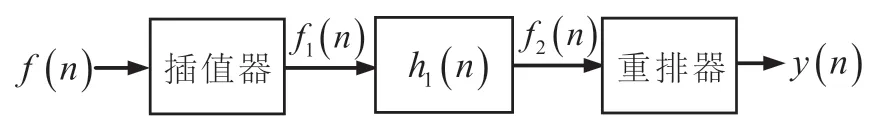
图2 实现截止频率变换的数字滤波器
(1)试求子数字带通滤波器h1(n)的频率特性H1(ejω)。
(2)试求整个系统的频率特性H(ejω),并与频率特性H1(ejω)进行比较。
(3)若激励f(n)=6(3-|n|)R7(n+3)*δ12(n),试求数字带通滤波器的零状态响应yf(n)。
解:(1)假设
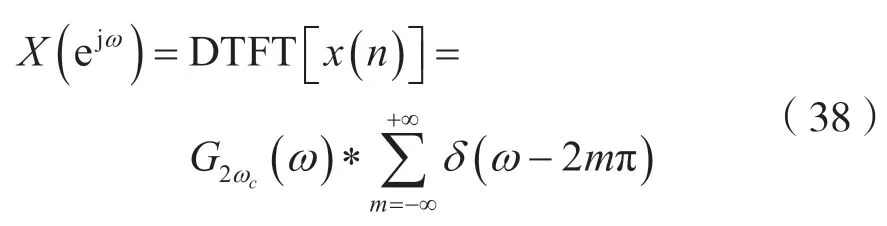
式中,0<ωc<π。
由式(38)可得:
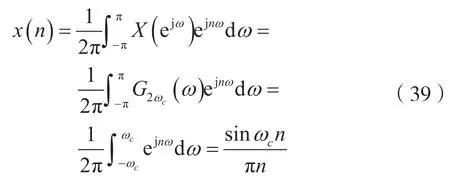
考虑到式(38)及式(39),则有:

式中:

由式(40)可得:

考虑到:

对式(43)两边取DTFT,并注意到DTFT的频移性质及式(42),则有:

(2)由题意可知:
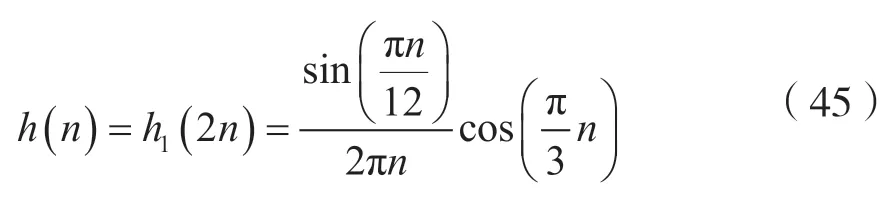
对式(45)两边取DTFT,并注意到式(40),可得:
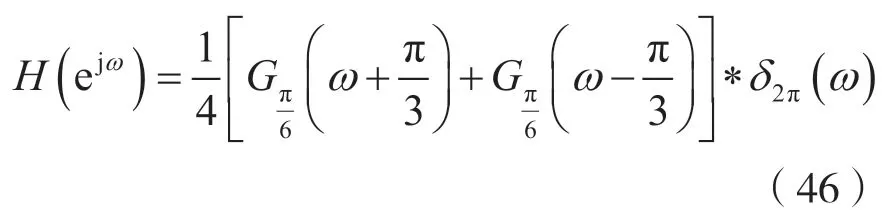
显然,ωL=2ωL1,ω0=2ω01,ωH=2ωH1。
(3)考虑到:

对式(47)两边取DTFT,则有:

考虑到式(46)及式(48),则图2 所示的数字带通滤波器的零状态响应的频谱为:

对式(49)两边取IDTFT,可得图2 所示的数字带通滤波器的零状态响应,即:

分析表明,周期为N=12 的三角波序列通过该数字带通滤波器时,输出为其二次谐波分量。
5 结语
本文揭示了插值、抽取及重排序列的z 变换与其频谱之间相互计算的方法。提出了一种数字滤波器前置插值器和后置重排器的级联结构,从时域和频域分析了该结构实现数字滤波器截止频率变换的原理,并给出了利用该结构来实现数字带通滤波器的截止频率变换,通过数字信号的滤波来选择所需数字信号的实例。

