实时信号处理中的信号拼接方法*
陈绍荣,朱行涛,徐 舜,沈建国
(陆军工程大学通信士官学校,重庆 400035)
0 引言
在实时信号处理中,通常用FFT的算法来完成线性卷和运算,因此需要对长序列进行分段,其分段方法有无重叠等长度分段和重叠等长度分段,对应的两种计算线性卷和的方法,分别是重叠相加法和重叠保留法。著作[1-3]用图解的方式导出了重叠相加法和重叠保留法,既不严谨又不便于理解。本文基于著作[4],利用矩形窗函数对序列的分段进行了描述,给出了一种导出重叠相加法和重叠保留法的简易方法,揭示了两种方法的联系和区别。解决了两种方法在实时信号处理中的信号拼接问题,给出了重叠保留法在快速计算自相关函数方面的应用。
1 圆周卷和代替线性卷和的条件
设矩形窗函数为:

式中,ε(n)为单位阶跃序列。
利用矩形窗函数,起点为n1(n1为整数),长度为N1的有限长序列x1(n)可表示为:

同理,起点为n2(n2为整数),长度为N2的有限长序列x2(n)可表示为:

有限长序列x1(n)和x2(n)的线性卷和yl(n)表示为:
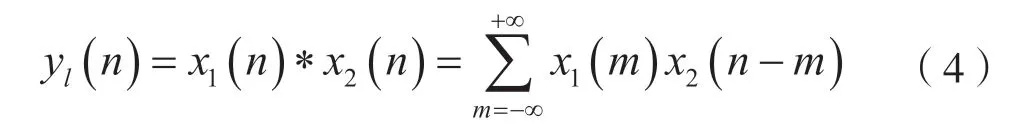
考虑到式(2)、式(3)及式(4),则有:
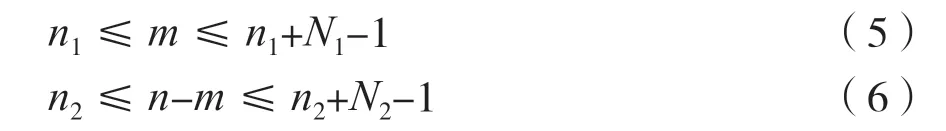
考虑到式(5)及式(6),则有:
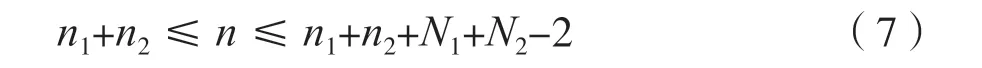
由式(7)可知,线性卷和yl(n)的序列长度为:
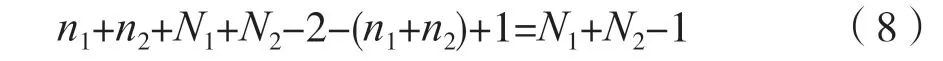
结论1:
两个有限长序列的线性卷和yl(n)是一个有限长序列,该有限长序列始于两个有限长序列的始点之和,止于两个有限长序列的终点之和,其序列长度为两个有限长序列的长度相加再减1。
利用矩形窗函数,考虑到式(7)及式(8),则线性卷和yl(n)可以表示为:
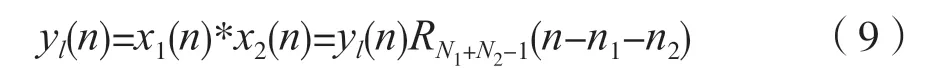
设周期为N的周期冲激序列为:
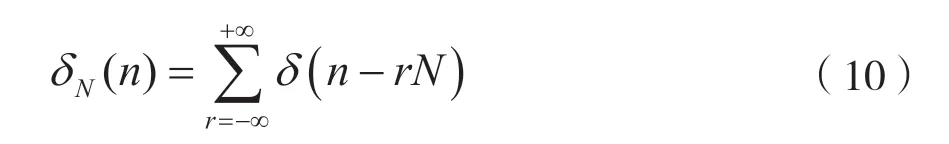
在式(2)及式(3)描述的有限长序列x1(n)及x2(n)之后,分别补上N-N1及N-N2个零值点,再延拓成周期为N的周期序列,即:
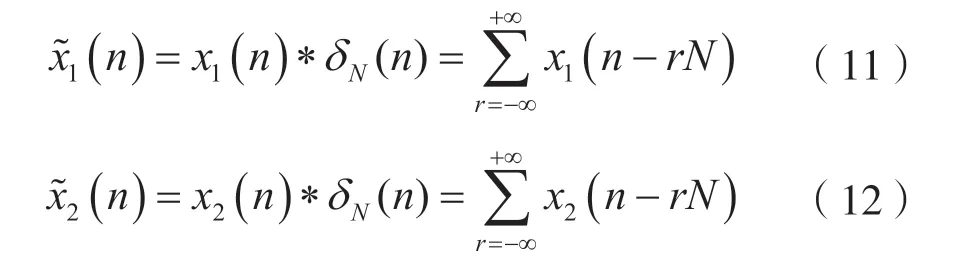
由两个周期序列的周期卷和的定义,并考虑到周期序列在一周期内的求和与起始位无关及式(11),则两个周期序列的周期卷和可以表示为:
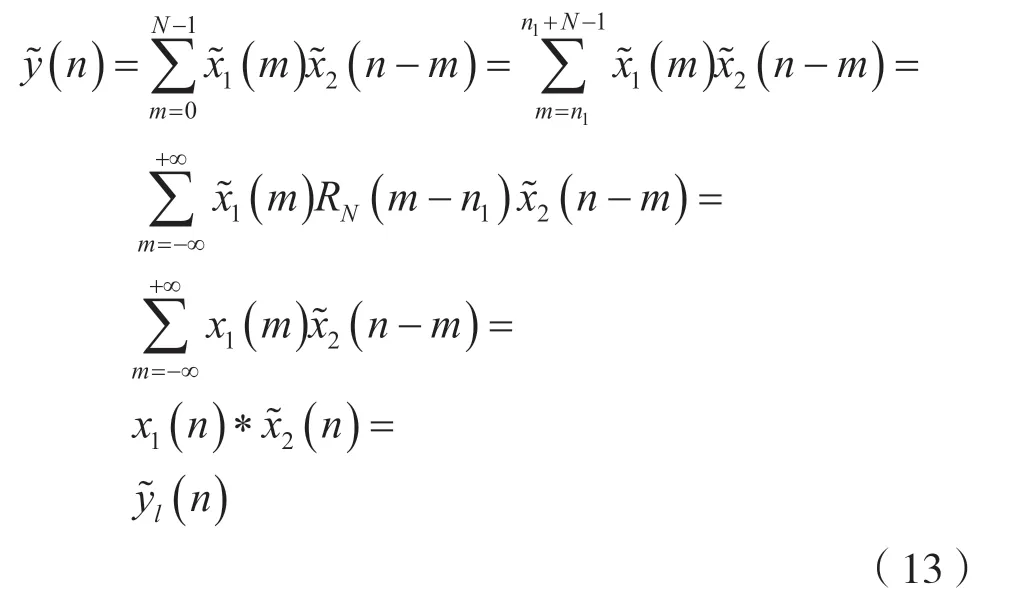
结论2:
两个周期序列作周期卷和等价于一个周期序列任一周期内的序列和另一个周期序作线性卷和,也等价于对两个周期序列任一周期内的序列的线性卷和作同周期的周期延拓。
将两个有限长序列x1(n)及x2(n)之后,先分别补上N-N1及N-N2个零值点,得到了两个长度为N的序列,再分别作周期为N的周期延拓,得到了周期为N的周期序列的周期卷和取主值,即取区间[0,N-1]对应的值,定义为N点序列x1(n)及x2(n)的N点圆周卷和y(n)。
考虑到两个N点序列的N点圆周卷和的定义及式(13),则N点序列x1(n)及x2(n)的N点圆周卷和y(n)可以表示为:
结论3:
两个N点序列作N点圆周卷和,等价于两个N点序列的线性卷和作N点的周期延拓,再取其主值序列。
考虑到式(15)及式(9),若满足条件:
则有:

特别地
若满足条件:

则有:

若满足条件:

则有:

结论4:
若序列x1(n)=x1(n)RN1(n),x2(n)=x2(n)RN2(n),当N=N1+N2-1 时,则满足式(21)的条件,那么可用序列x1(n)和x2(n)的N点圆周卷和y(n)来代替序列x1(n)和x2(n)的线性卷和yl(n)。
若序列x1(n)=x1(n)RN1(n),x2(n)=x2(n)RN2(n),当 式(21)的条件得不到满足时,由式(14)可知,将序列x1(n)和x2(n)的线性卷和yl(n)作周期延拓,即yl(n)*δN(n)=yl(n)RN1+N2-1(n)*δN(n),那么,每周内将出现重叠。虽然增加点数N可避免序列x1(n)和x2(n)的N点圆周卷和y(n)出现重叠,但是使用FFT来计算N点圆周卷和y(n)时,将会增加运算量。
由于序列x(n)通过单位冲激响应为h(n)的LSI离散时间系统时,系统的零状态响应yzs(n)可以表示成yzs(n)=x(n)*h(n),有时序列x(n)可能会很长,如果将序列x(n)存储完毕后,再做线性卷和将产生两个问题:一是要求计算机的存储量过大,二是要等待序列x(n)的输入时间过长,即使h(n)是有限长的,也不能实现信号的“实时处理”。为了解决这一问题,如果h(n)的长度为N2,选取长度N1,保证M为最小的正整数时,满足条件N=N1+N2-1=2M,将长度为L的输入序列x(n)按等长度N1进行分段,则第i段的序列可以表示为xi(n)=x(n)RN1(n-iN1),i=0,1,2,…,,其中表示大于或等于L/N1的正整数。将序列xi(n)及h(n)做线性卷和运算得到序列yi(n),然后将各段序列yi(n)按一定的规则相加,即可得到完整的零状态响应yzs(n),这样做有可能实现信号的实时处理。
将长序列分成短序列做线性卷和有两种方法,一是重叠相加法,二是重叠保留法。
2 重叠相加法
设序列x(n)=x(n)RL(n),h(n)=h(n)RN2(n),L和N2为正整数,并且L>>N2。
选取长度N1,保证M为最小正整数时,满足条件N=N1+N2-1=2M,将序列x(n)按等长度N1分段,则有:
式中:

考虑到式(23)及式(24),则有:
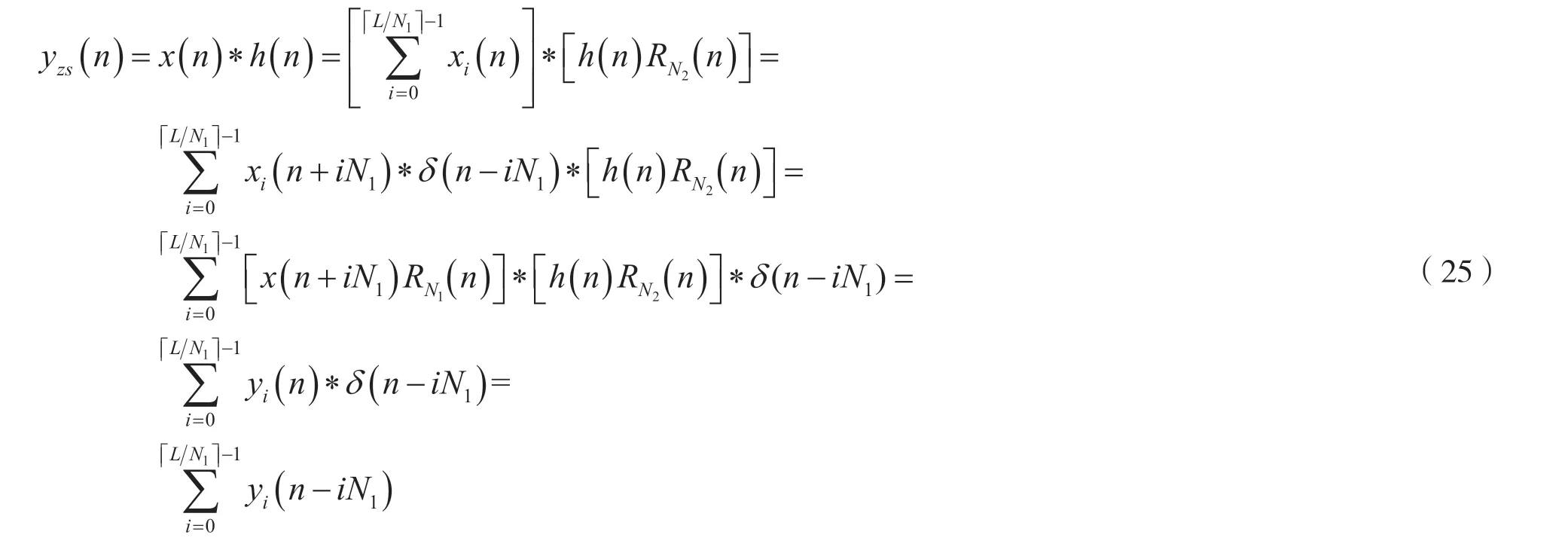
由 于N=N1+N2-1=2M,h(n)=h(n)RN2(n),xi(n+iN1)=x(n+iN1)RN1(n),由结论4 可知,可用序列x(n+iN1)RN1(n)和h(n)RN2(n)的N点圆周卷和来代替线性卷和。那么,式(25)中的yi(n)可表示为:
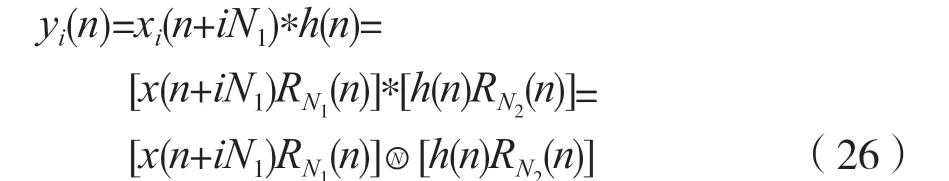
考虑到式(26),则可以利用FFT来计算LSI离散时间系统的零状态响应yzs(n),其实现步骤为:
(1)计算N 点FFT
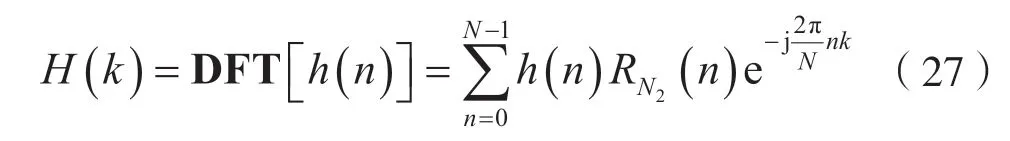
(2)计算N 点FFT
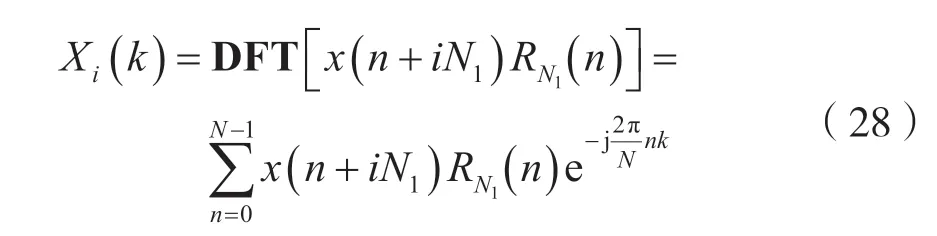
(3)相乘

(4)计算N 点IFFT
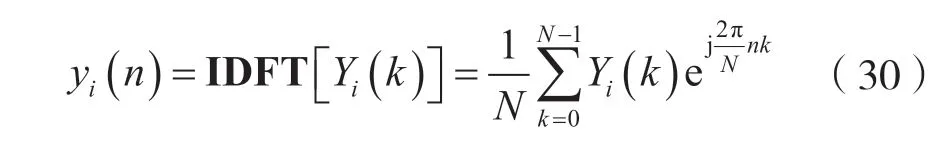
(5)将各段yi(n)按式(25)相加,即按式(25)完成LSI 离散时间系统的零状态响应信号的拼接。
讨论:
由结论1 可知,第i段xi(n)和h(n)RN2(n)的线性卷和yi(n-iN1)=xi(n)*h(n)RN2(n)和h(n)RN2(n)中的变量n的取值范围为:
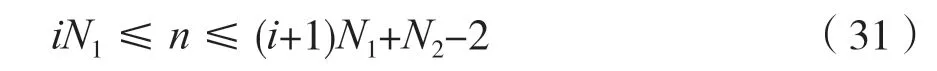
由结论1 可知,第i-1 段xi-1(n)和h(n)RN2(n)的线性卷和y(i-1)[n-(i-1)N1]=xi-1(n)*h(n)RN2(n)中的变量n的取值范围为:
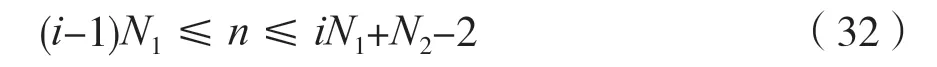
由式(31)及式(32)可知,第i-1 段的线性卷和y(i-1)[n-(i-1)N1]的末端与第i段的线性卷和yi(n-iN1)的前端将出现重叠,其重叠的长度为:

结论5:
由式(33)可知,按式(25)的重叠相加法来计算LSI 离散时间系统的零状态响应时,相邻段的线性卷和将出现N2-1 点的重叠相加运算,故得名重叠相加法。
考虑到h(n)=h(n)RN2(n),则有:
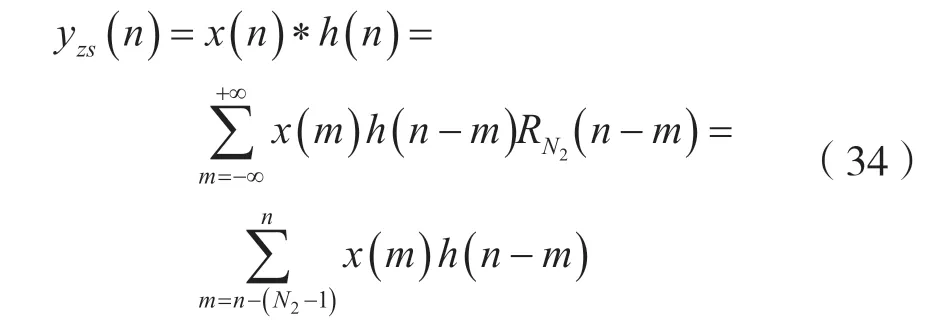
于是:
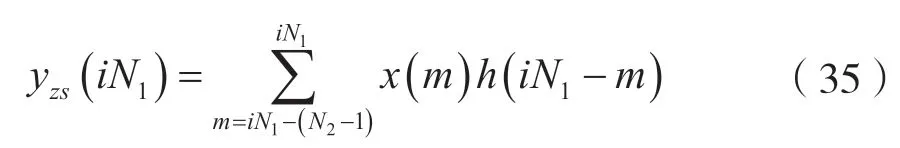
式中,i=1,2,…,。
由式(35)可知,yzs(iN1)由xi(n)的首位数据xi(iN1)=x(iN1)及首位之前的N2-1 个点的输入数据x(m)(m=iN1-N2+1,iN1-N2+2,…,iN1-1)
共同确定。
结论6:
用对输入x(n)等长度N1分段的线性卷和来计算LSI 离散时间系统的零状态响应时,出现重叠相加运算的本质是第i段首位之前的N2-1 点的输入数据x(m),对第i段前N2-1 点的线性卷和有影响。
3 重叠保留法
由于用对x(n)等长度N1分段的线性卷和来计算LSI 离散时间系统的零状态响应时,出现了重叠相加运算,为了避免重叠相加运算,可以将第i段首位之前的N2-1 点输入数据x(n)保留下来与第i段的序列xi(n) 依次衔接起来,构成一个长度为N=N1+N2-1 的 新 序 列pi(n)(i=1,2,…,,考虑到x(n)=x(n)RL(n),只须在x0(n)=x(n)RN1(n)段的前端补上N2-1 个零值点,便可构成新序列p0(n),这样各段pi(n)均为N1+N2-1 点的序列。即:
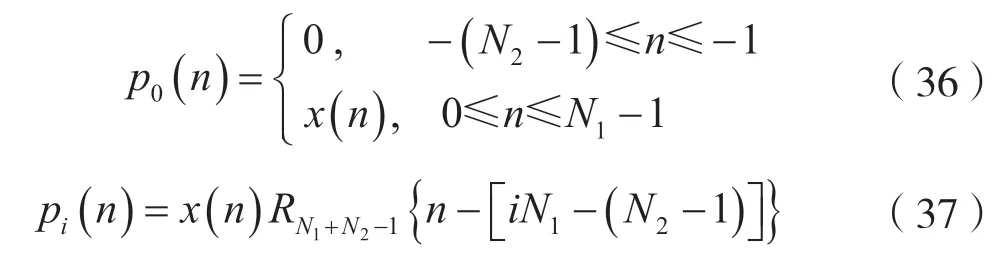
式中,i=1,2,…,。
考虑到式(36)及式(37),则长度为N1+N2-1 的序列pi(n)和LSI 离散时间系统单位冲激响应h(n)的线性卷和yli(n)(i=0,1,2,…,,可以表示为:
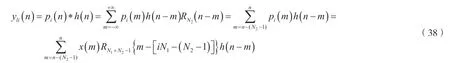
下面确定n在什么范围内取值时,才能使yli(n)=yzs(n)。
对比式(38)和式(34)可知,为使线性卷和yli(n)=yzs(n),则要求:
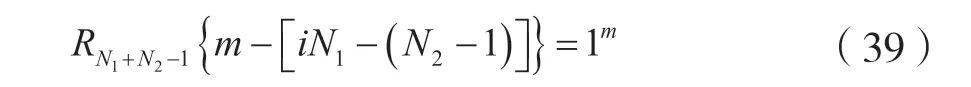
式中,m为整数。
显然,若满足条件:
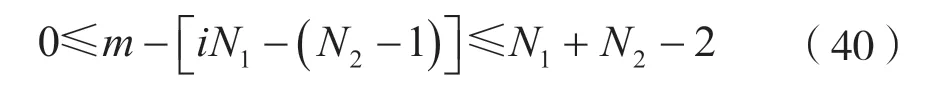
则式(39)恒成立。
即,若满足条件:
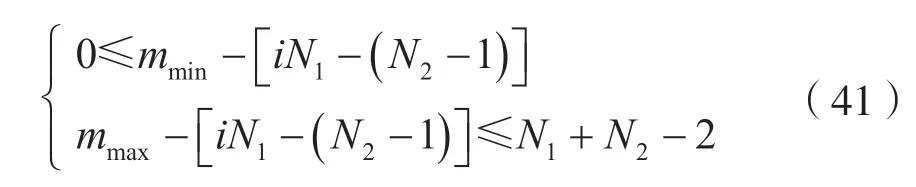
则式(39)恒成立。
由式(38)和式(34)可知,mmin=n-(N2-1),mmax=n。
于是式(41)可以表示为:
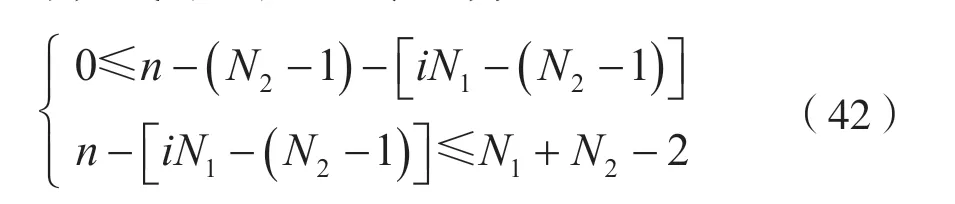
解得:

由式(43)可知,其区间长度为:

考虑到式(43)及式(44),则有:
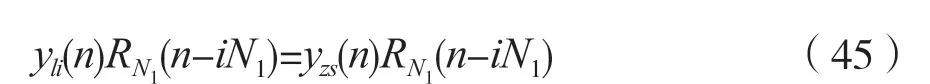
考虑到式(45),则有:
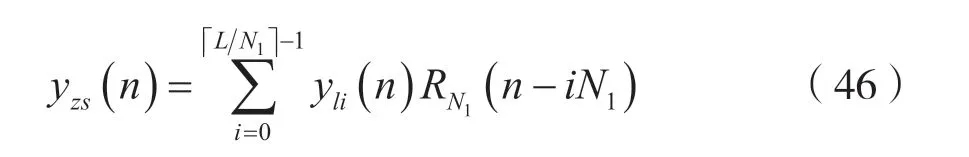
分析表明,将各段pi(n)和LSI 离散时间系统单位冲激响应h(n)的线性卷和yli(n),按式(46)逐段衔接(或拼接)起来,就得到了LSI 离散时间系统的零状态响应yzs(n)。
下面的任务是考察是否可用圆周卷和来替代线性卷和yli(n)。
考虑到h(n)=h(n)RN2(n),式(36)及式(37),并注意到N=N1+N2-1=2M,由结论1 可知,pi(n)和LSI 离散时间系统单位冲激响应h(n)的线性卷和yli(n)(i=0,1,2,…,,可以表示为:
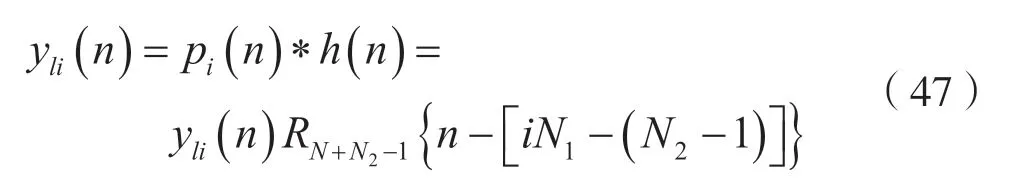
于是:
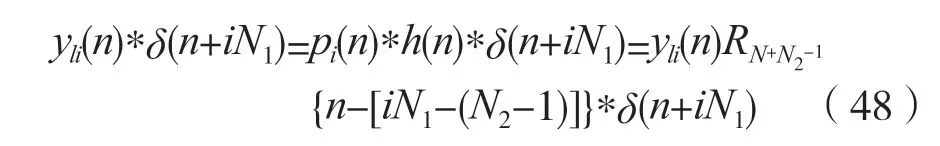
即:
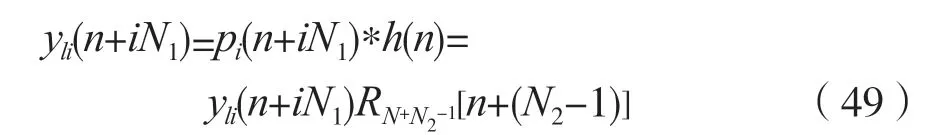
考虑到式(49),由结论3 可知,pi(n+iN1)和h(n)的N点圆周卷和yi(n+iN1)可以表示为:
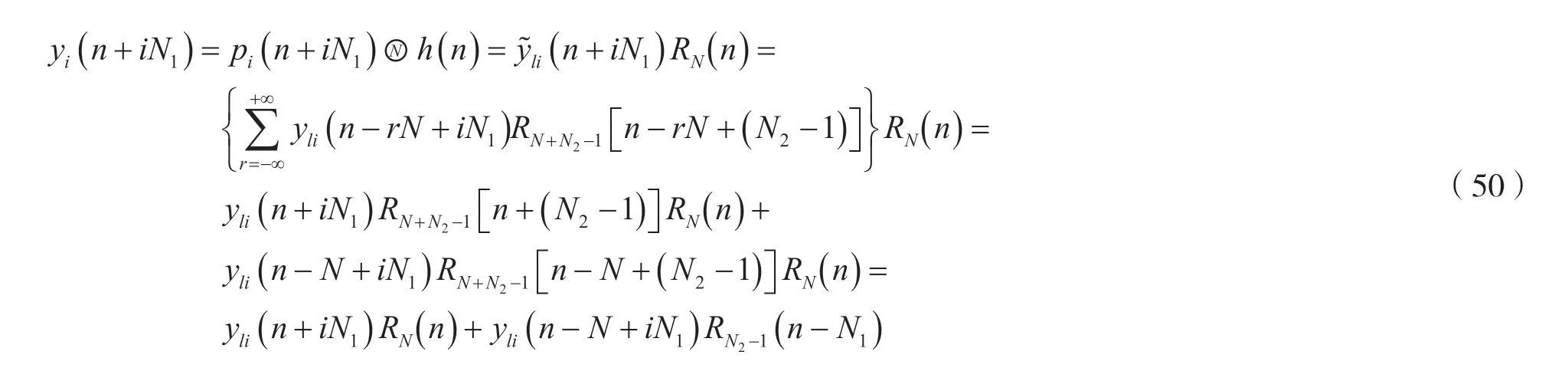
由式(50)可得:
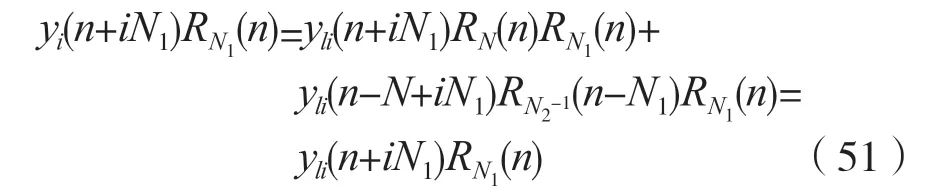
考虑到式(51),则式(46)可以写成:
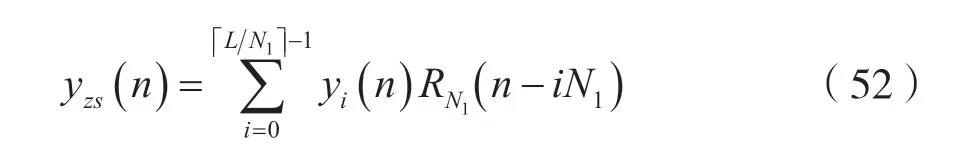
考虑到式(50),则可以利用FFT来计算LSI离散时间系统的零状态响应yzs(n),其实现步骤为:
(1)计算N 点FFT

(2)基于式(36)及式(37),计算N 点FFT

(3)相乘

(4)计算N 点IFFT

(5)将各段yi(n+iN1)按式(52)逐段衔接(或拼接)起来,就得到了LSI 离散时间系统的零状态响应yzs(n)。
由式(36)及式(37)可知,将第i段首位之前的N2-1 点输入数据x(n)保留下来,与第i段xi(n)依次衔接起来构成了pi(n),从而使pi-1(n)的末端与pi(n)的前端N2-1 点的数据相同,即pi-1(n)与pi(n)之间有N2-1 点的数据重叠,故得名重叠保留法。由式(50)可知,pi(n+iN1)和h(n)的N点圆周卷和yi(n+iN1)末端出现了N2-1 点的重叠数据,由式(51)可知,将pi(n+iN1)和h(n)的N点圆周卷和yi(n+iN1)末端N2-1 点的重叠数据舍去,才保证了pi(n+iN1)和h(n)的圆周卷和等于线性卷和,故又得名重叠舍去法。
4 重叠保留法在快速计算自相关方面的应用
设序列x(n)=x(n)RL(n),先将x(n)按长度N2分段,则第j段可以表示为:

式中,j=0,1,2,…,。
于是:
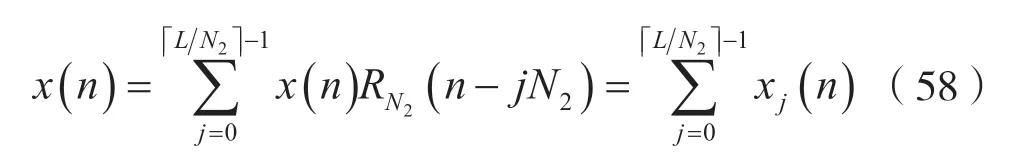
现在,构成各段pi(n)均为N=N1+N2-1=2M点的序列,即:
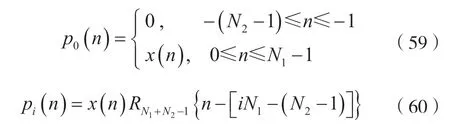
式中,i=1,2,…,。
令:

考虑到式(57),则式(61)可以表示为:
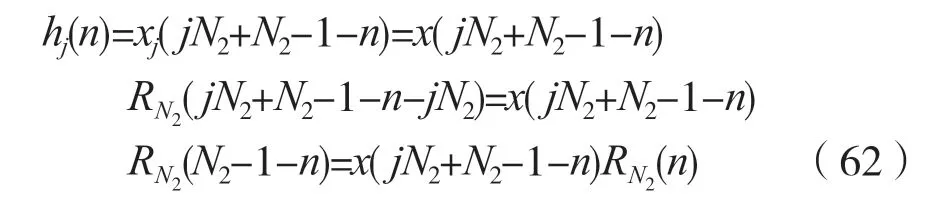
式(62)表明,hj(n)是一个长度为N2点的序列,并且满足hj(n)=hj(n)RN2(n)。
考虑到序列自相关函数的定义及式(58),则序列x(n)的自相关函数Rx(n)可以表示为:
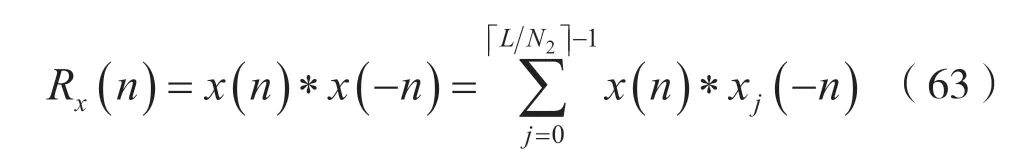
令:

则有:
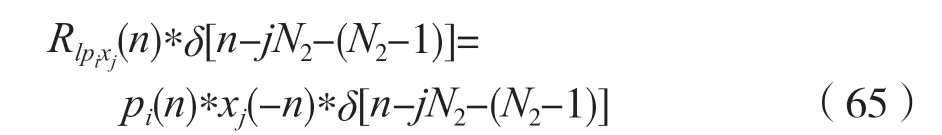
考虑到式(61),则式(65)可以写成:
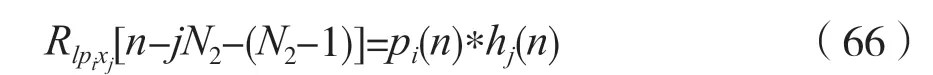
式中,i=0,1,2,…,-1。
由于式(66)与式(47)同形,考虑到式(52),则有:
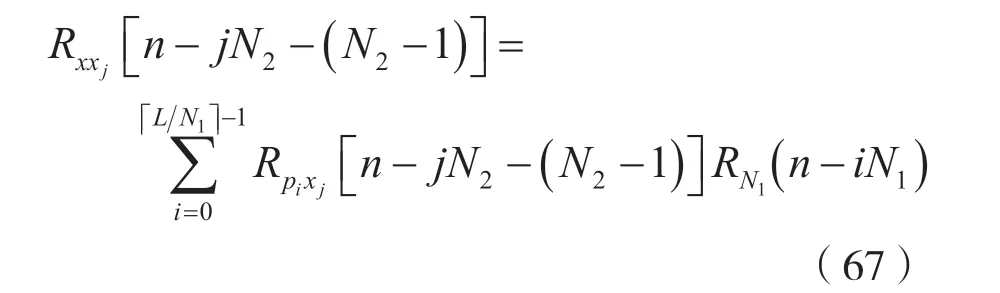
式 中,Rpixj[n+iN1-jN2-(N2-1)]为pi(n+iN1) 和hj(n)的N点圆周卷和。
考虑到式(66),由结论3 可知:
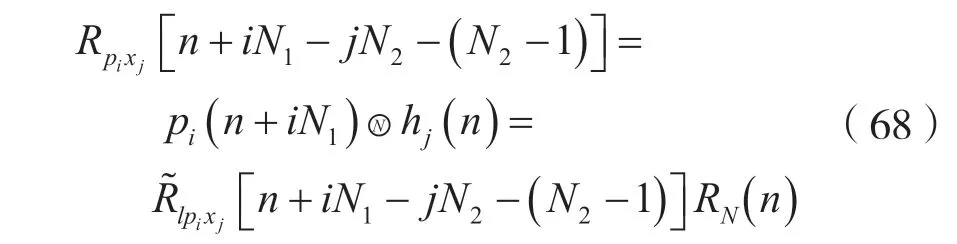
考虑到式(67),则有:
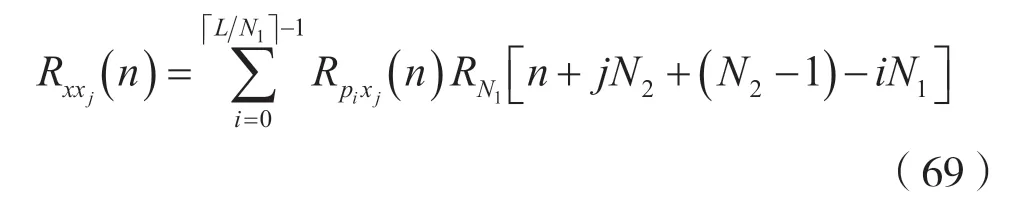
将式(69)代入式(63),可得序列x(n)的自相关函数Rx(n),即:
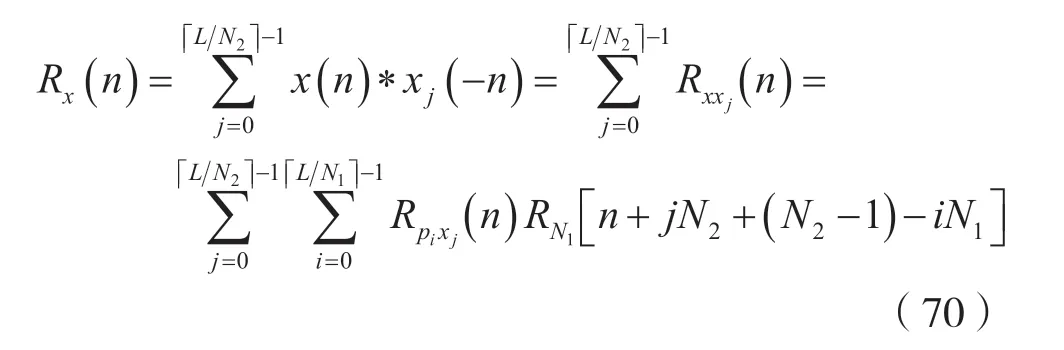
考虑到式(68),则可以利用FFT 来计算序列x(n)的自相关函数Rx(n),其实现步骤为:
(1)基于式(59)及式(60),计算N 点FFT

(2)基于式(61),计算N 点FFT

(3)相乘

(4)计算N 点IFFT
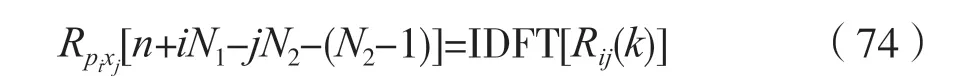
(5)将各段Rpixj[n+iN1-jN2-(N2-1)],按式(70)相加,即完成自相关函数的拼接,就得到了自相关函数Rx(n)。
5 结语
本文利用矩形窗函数对输入序列的等长度N1分段进行了描述,分析了用对输入x(n)等长度N1分段的线性卷和来计算LSI 离散时间系统的零状态响应时,出现重叠相加运算的原因。不仅给出了一种导出重叠相加法和重叠保留法的简易方法,而且揭示了重叠相加法和重叠保留法的联系和区别。解决了两种方法在实时信号处理中的信号拼接问题,最后给出了重叠保留法在快速计算自相关函数方面的应用。

