基于SSFT-PE 表面粗糙隧道电波传播研究*
吉 熙,廖 成,张东民,邓小川,冯 菊
(西南交通大学 电磁场与微波技术研究所,四川 成都 610031)
0 引言
矿井、铁路及公路等通信需求,使得隧道中的电波传播特性研究一直深受国内外学者的关注[1]。传统上,隧道被建模为理想光滑壁,很少考虑到表面随机粗糙对电波传播特性的影响。而最近随着5G 时代的来临和无人驾驶技术的应用需要,精确的隧道电磁态势分布的重要价值愈加凸显。因此,粗糙表面的隧道电波传播研究具有重要意义。
在大尺度的隧道电波传播预测分析中,目前已经有许多数值方法提出,如射线追踪法[1]、模式理论[2-3]和抛物方程方法。其中,射线追踪法利用几何光学原理追踪由发射源发出的每条射线的传播路径,计算出其与周围环境所发生的反射作用,根据给定的条件判断其是否能够到达接收天线;计算每一条收发天线之间的路径,并存储其总长度和每一次反射系数;利用叠加原理计算到达接收天线的所有路径的信号总能量[4]。在简单的隧道场景,射线追踪法非常有效。但是,对于复杂的隧道场景,该方法计算过程十分繁琐。模式理论是由麦克斯韦方程组在特定的边界条件下推导而来的,假设电波是以不同模式的组合进行传播[3]。模式理论是解析解,计算精度高,但仅适用于少数形状规则、简单的隧道环境。抛物方程(Parabolic Equation,PE)由波动方程推导而来[5],采用步进迭代的方式进行求解。引入分布傅里叶变换技术(Split-step Fourier Transform,SSFT)[6]或交替方向隐式差分技术(Alternating Direction Implicit,ADI)[7-8]后,在保证计算精度的同时,也保证了很高的运算效率,非常适用于隧道中的电波传播预测。目前,人们对抛物方程应用于隧道的研究还主要集中在光滑壁上。虽然R.Martelly 与R.Janaswamy 使用PE 的ADI 解法研究了粗糙隧道的电波传播,但并未研究半圆拱形截面隧道的电波传播[7]。Xingqi Zhang 研究了粗糙半圆拱形的隧道电波传播,采用ADI 方法。为了保证差分格式的稳定性和计算精度,通常要求较小的计算步长,影响了求解效率[9]。
针对上述问题,本文提出了一种基于SSFTPE 的粗糙隧道电波传播计算方法。通过在传统的SSFT-PE 基础上引入等效粗糙因子,得到能应用于表面粗糙隧道的修正模型,既能兼顾解算精度又能保证求解效率。本文首先回顾了隧道中模式分析方法,其次详细介绍了基于SSFT-PE 的表面粗糙隧道电波传播计算方法,最后结合数值算例,将本文方法与模式分析方法的计算结果进行对比验证,并利用本文方法分别研究了矩形隧道结构与半圆拱形隧道结构下,不同粗糙程度和不同电磁波频段对隧道电波传播的影响。
1 模式分析方法
对于形状规则、结构简单的隧道环境,模式理论能够得到隧道内场分布的解析解。模式理论认为,隧道中的场分布是一系列不同模式EHp,q的加权组合,其中下标p和q表示模式的阶数。矩形隧道如图1所示,隧道内任意位置的电场可由式(1)求出[1]:

其中,Ap,q是本征模函数,Et是由发射功率决定的发射电场,随机粗糙衰减常数和相位常数分别为:
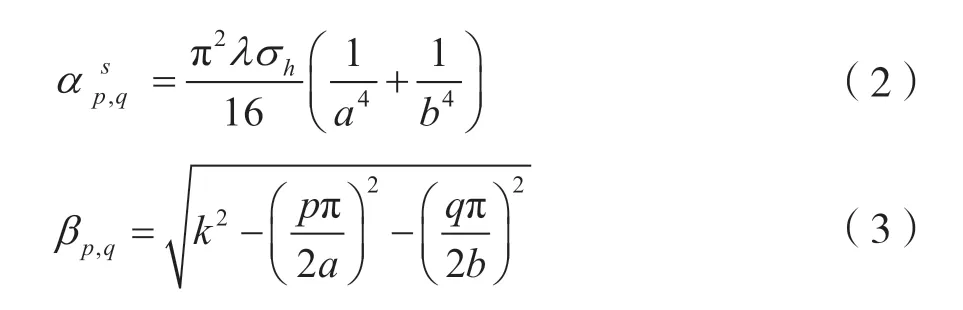

图1 矩形隧道
(1)平行极化时,Ap,q、αp,q由式(4)与式(5)求出:

(2)垂直极化时,Ap,q、αp,q由式(6)与式(7)求出:
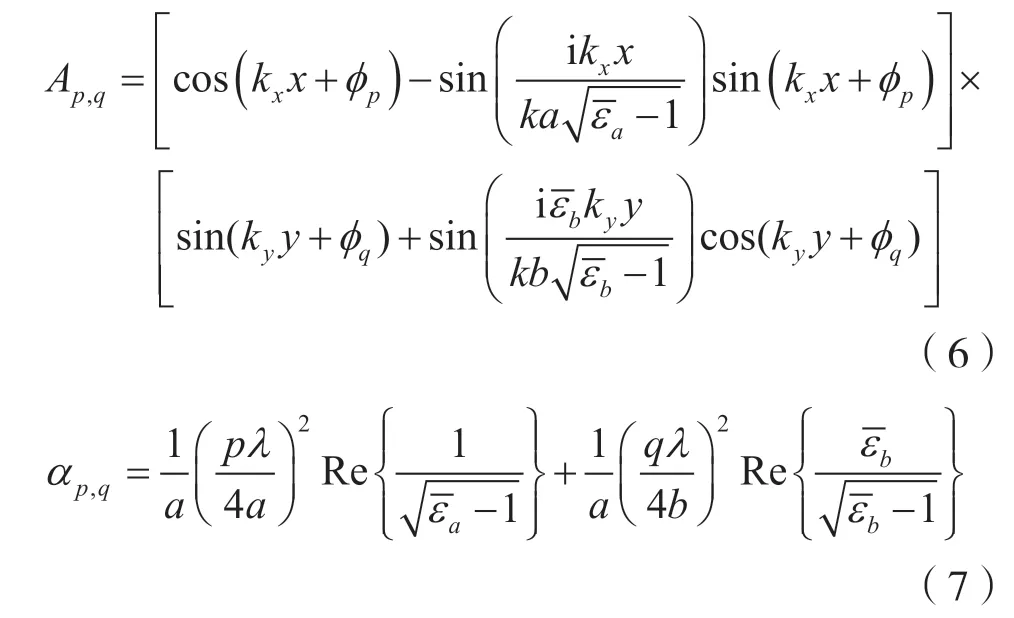
其中:

复介电常数可由式(9)表示:

其中,εra,b是侧壁和上下壁的相对介电常数,σa,b是侧壁和上下壁的电导率。
2 基于SSFT-PE 的表面粗糙隧道电波传播计算方法
2.1 SSFT-PE 基本理论
在直角坐标系(x,y,z)中,假设电磁场的时谐因子为e-iwt,电场或磁场分量ψ满足如式(10)形式的三维标量Helmholtz 方程[10]:

其中ψ是任意方向的电磁场分量,为拉普拉斯算子,为介质折射指数。令沿z轴正方向传播的波函数为u(x,z)=e-ik0zψ(x,y,z),代入式(10)并对其进行因式分解可得:
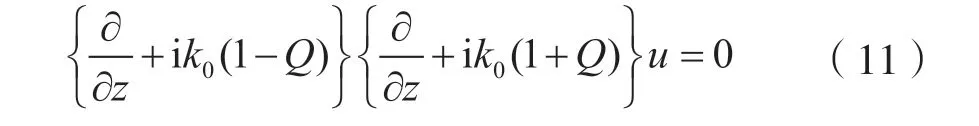
其中Q为伪微分算子:

这里仅考虑电磁波的前向传播,得到前向抛物方程为:
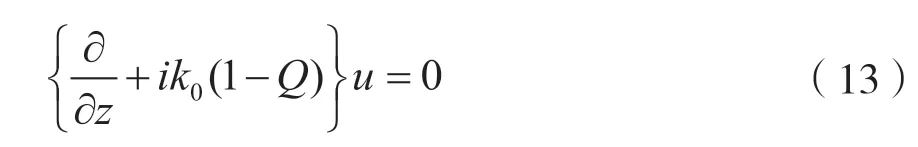
将伪微分算子Q进行Feit-Fleck 分解得到:

将式(14)代入式(11),得到如式(15)形式的抛物方程:

对式(11)采用分步傅里叶变换(Split-Step Fourier Transfrom,SSFT)算法进行求解,可以得到如式(16)形式的递推公式[11]:

其中,ℑ2与分别表示二维傅里叶正变换和逆变换。二维傅里叶变换可以通过二维FFT 技术实现快速计算,因此SSFT 算法是一个高效的解算算法。
2.2 适用于表面粗糙隧道的修正SSFT-PE 方法
2.2.1 介质隧道计算方法
对每种本征模而言,根据欧拉定理可以将本征模式展开为两种平面波的叠加。边界条件为第一类时对应奇对称,镜像场为负场,而第二类边界条件对应偶对称,镜像场为正场。因此,将矩形隧道进行2 次镜像后,原计算域扩展为4 倍。通过计算域的扩展和镜像场的填充,可以等效考虑隧道的两类边界条件。根据各模式本征函数可以求出其对应的入射角,由入射角可以算出隧道内对应方向反射一次时对应的距离[12]:

传播距离为z时,平面波在介质壁上的损耗L可以通过式(18)和式(19)得到:

其中L0代表抛物方程的计算过程中不同模式的本征损耗,ρ⊥,||是反射系数。kx与ky代表沿x与y方向的传播常数,k0是自由空间中电磁波的波数。因此,介质矩形隧道环境中的递推公式为:

在实际隧道工程中,通常半圆拱形截面形状的隧道十分常见[13],见图2。
图2 半圆拱形隧道截面形状
文献[12]给出了介质半圆拱形隧道环境中的递推公式:
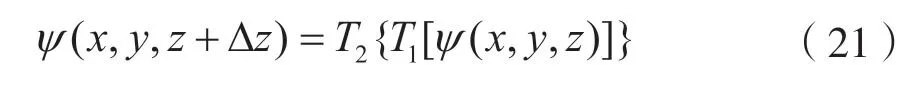
令:


则有:
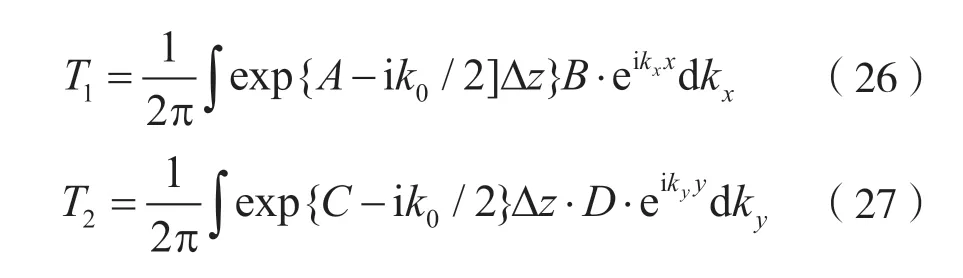
2.2.2 表面粗糙隧道计算方法
对于均匀平面波入射到光滑壁的情况,可以由菲涅尔定律计算出反射系数[14],如图3 所示。

图3 光滑壁对平面波的反射
此时,菲涅尔反射系数为:

其中,⊥,||分别表示垂直极化和平行极化,α⊥,||是入射角,且有:

一般来说,粗糙表面对电磁波的反射通过统计学方法进行量化。目前,常认为粗糙表面符合均值u为0、标准差为σh的高斯分布。当σh<<λ时,由于粗糙表面造成的反射系数为[1]:

将式(32)与式(28)相乘,可得到修正后粗糙表面的反射系数:

将式(33)代入式(18)和式(19),即得到计算矩形粗糙隧道的修正SSFT-PE 算法。同理,将式(33)代入式(21)、式(26)和式(27),即得到计算半圆拱形粗糙隧道的修正SSFT-PE 算法。
3 数值算例分析
由于现代工程施工的精度越来越高,根据生活实践经验以及文献[1]等参考可以得出,现代隧道的σh不会太大。为了不失一般性,本文选取σh满足如下条件:

在验证算例中,选取σh=0 cm 与σh=10 cm;电波传播特性分析中,研究不同σh对矩形隧道电波传播的影响时,为了同时满足σh<<λ的条件,故选取σh=0 cm、σh=3 cm、σh=5 cm 与σh=7 cm;研究不同频率下σh对传播因子的影响时,选取σh=5 cm。
3.1 验证算例
为了验证本文算法处理粗糙隧道的正确性,分别采用修正后PE 法与模式理论法计算矩形粗糙隧道地形下传播因子随距离的变化。
矩形隧道参数见表1,仿真条件设置为高斯反射源频率0.9 GHz,波瓣宽度为4.34°,垂直极化波与水平极化波,天线安置在隧道中心位置,接收天线高度为3 m,发射天线高度为3 m。图4(a)是PE 方法与模式理论垂直极化时传播因子随传播距离变化的对比。当σh=10 cm 时,PE 方法与模式理论吻合得很好。图4(b)是PE 方法与模式理论水平极化时传播因子随传播距离变化的对比。当σh=10 cm 时,PE 方法与模式理论吻合得很好。图4证明了修正后的PE 算法计算粗糙隧道的正确性。
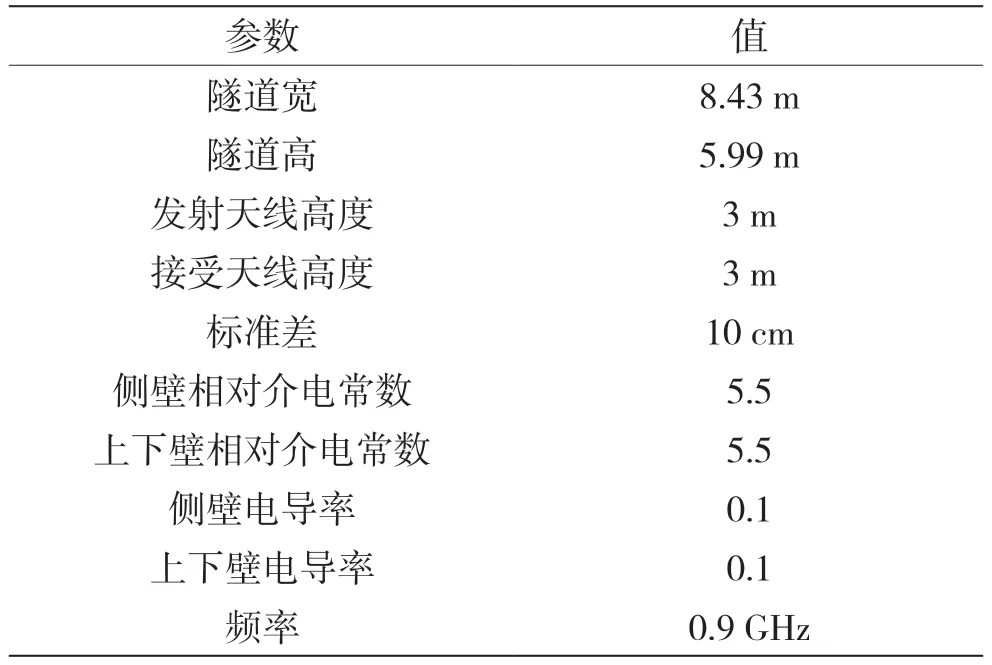
表1 矩形隧道参数

图4 抛物方程与模式理论的对比
3.2 粗糙隧道的电磁波传播特性研究
3.2.1 矩形隧道电波传播特性分析
为了研究不同σh对矩形隧道电波传播的影响,仿真不同σh时传播因子随传播距离的变化,如图5所示。为了定量研究不同σh对传播因子的影响,,其 中F1(i) 表 示σh=0 cm 时的传播因子,F2(i)表示在给定频率下σh=3 cm、5 cm、7 cm时沿x轴线方向各网格点的传播因子。表2 与表3分别给出了2.515 GHz 与2.675 GHz下不同σh的RMSE。隧道参数如表1 所示,仿真条件设置为高斯反射源频率分别为5G 频率2.515 GHz、2.675 GHz,波瓣宽度为4.34°,垂直极化波,天线安置在隧道中心位置,接收天线高度为3 m,发射天线高度为3 m。从图5 可以看出,在近场处出现了信号的快衰落,这是由于电波受到隧道壁的作用会产生多次反射,这些反射的分量会产生许多多径分量形成频率选择性信道,造成信道的快衰落。另外,随着传播距离的增加,越大的σh传播因子,电波传播的损耗越大,这是由于粗糙壁对无线电波的额外散射损耗造成的。
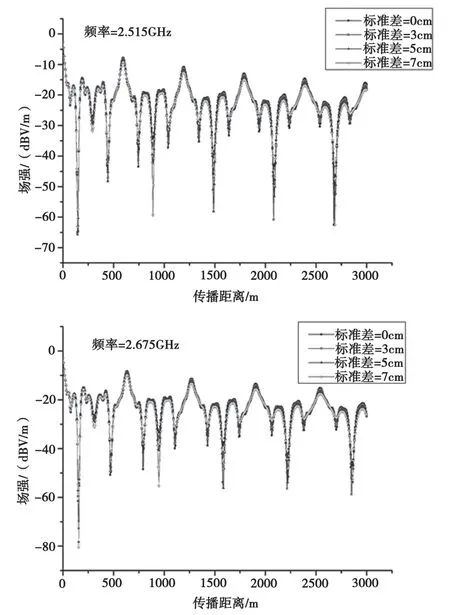
图5 不同σh 时传播因子随距离的变化

表2 f=2.515 GHz 时不同σh 的RMSE

表3 f=2.675 GHz 时不同σh 的RMSE
为了研究在相同σh不同频率下对传播因子的影响,定义,其中F1(i)表示σh=0 cm 时的传播因子,F2(i)表示在给定频率下σh=5 cm 时沿x轴线方向各网格点的传播因子。图6 显示了垂直极化与水平极化条件下,在σh=5 cm时不同频率下MSE的变化。其中,2.515~2.675 GHz、3.4~3.5 GHz 与3.5~3.6 GHz 分别属于中国移动、中国电信与中国联通的5G 通信频段。表4 给出了频 率 为2.515 GHz、2.675 GHz、3.4 GHz、3.5 GHz与3.6 GHz 的RMSE,表5 给出了0.5~2.4 GHz 的平均RMSE以及这几个5G 频点的平均RMSE。从图6 可以看出,当f从0.5 GHz 开始变化到3.6 GHz,RMSE整体在增加,表明发射频率越高,微小的σh将对电波的传播因子造成显著影响;从表4 可以看出,0.5~2.4 GHz 时,垂直极化时平均MSE达到0.831 2 dB,而在水平极化时达到了0.521 3 dB;在5G 通信频段,垂直极化时平均MSE达到了约2.5 dB,水平极化时平均MSE达到了约2.1 dB,明显高于0.5~2.4 GHz 的平均MSE,说明在5G 通信频段σh对电波的传播影响显著。

表4 不同频点下的平均RMSE
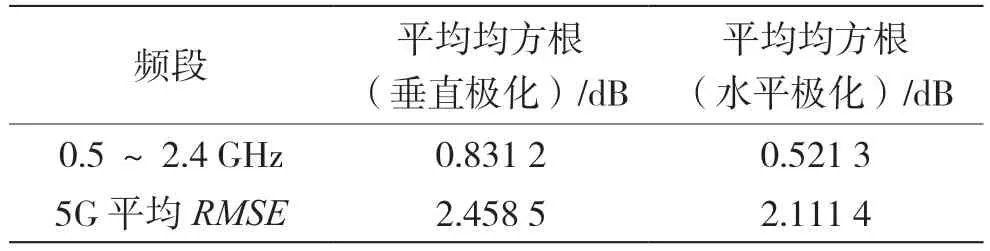
表5 不同频段下的平均RMSE

图6 不同频率下RMSE 的变化
3.2.2 半圆拱形隧道电波传播特性分析
为了研究不同σh对半圆拱形隧道电波传播的影响,仿真不同σh时传播因子随传播距离的变化。如图7 所示,为了定量研究不同σh对传播因子的影响,表6 与表7 分别给出了2.515 GHz 与2.675 GHz 下不同σh的RMSE。半圆拱形隧道的参数为W=8.43 m、H=5.99 m,仿真条件设置为高斯反射源频率分别为2.515 GHz、2.675 GHz,波瓣宽度为4.34°,εr=5.5,σ=0.1 S/m。天线安置在隧道中心位置,发射天线高度为3 m,垂直极化波,接收天线高度为3 m。从图7 可以看出,随着传播距离的增加,越大的σh传播因子,电波传播的损耗增加,与不同σh对矩形隧道电波传播的影响的结论相同。

图7 不同σh 时传播因子随距离的变化

表6 f=2.515 GHz 时不同σh 的RMSE

表7 f=2.675 GHz 时不同σh 的RMSE
图8 是垂直极化与水平极化条件下半圆拱形隧道中不同频率下σh对传播因子的影响。为了与矩形隧道中电波传播特性进行比较,设半圆拱形隧道的参数也为W=8.43 m、H=5.9 m,仿真条件设置为高斯反射源频率,波瓣宽度为4.34°,εr=5.5,σ=0.1 S/m。发射天线高度为3 m,接收天线高度为3 m。表8给 出 了2.515 GHz、2.675 GHz、3.4 GHz、3.5 GHz与3.6 GHz 的RMSE,表9 给出了0.5~2.4 GHz 的平均RMSE和这几个5G 频点的平均RMSE。从图8 可以看出,当f从0.5 GHz 开始变化到3.6 GHz,RMSE整体在增加,表明发射频率越高,微小的σh将对电波的传播因子造成显著影响;从表8 可以看出,0.5~2.4 GHz 时,垂直极化时平均RMSE达到了0.858 9 dB,而在水平极化时达到了0.744 9 dB;在5G通信频段,垂直极化时平均RMSE达到了约2.6 dB,水平极化时平均RMSE达到了约2.1 dB,明显高于其他频段,说明在5G 通信频段时σh对电波的传播影响显著。另外,比较图6 与图8 可以看出,矩形隧道的RMSE在2.0~2.4 GHz 时波动明显,而半圆隧道的RMSE在2.8~3.6 GHz 时波动明显;垂直极化的额外粗糙损耗大于水平极化时。

表8 不同频点下的平均RMSE

表9 不同频段下的平均RMSE

图8 不同频率下RMSE 的变化
4 结语
本文提出了一种基于SSFT-PE 的粗糙隧道电波传播模型。根据粗糙壁服从高斯分布统计下的反射系数模型,将该模型与传统的SSFT-PE 相结合,得到修正后的粗糙隧道传播模型,为预测真实隧道环境中的电波传播特性提供了一种快速准确的方法。在8.43 m×5.99 m 的典型矩形和拱形隧道中进行仿真分析,结果表明:当随机粗糙标准差σh等于5 cm 时,在0.5~2 GHz 频段,随机粗糙带来额外的约0.5 dB 损耗;在2~3.6 GHz 频段,随机粗糙带来额外的2.1 dB 损耗,在5G 频段的损耗大于其他低频段;在相同仿真频率下,额外的损耗随着粗糙程度的增加而增加。

